2. 中国人民解放军96712部队,江西省景德镇市,333300;
3. 哈尔滨工业大学(深圳)空间科学与应用技术研究院,深圳市平山一路6号,518055;
4. 中国人民解放军61206部队,北京市,100042;
5. 中国人民解放军96711部队,安徽省池州市,247100
针对GNSS坐标时间序列粗差探测与剔除的研究很多,Pernetti[1]利用DIA(detection identification adaptation)方法对GPS坐标时间序列的粗差和中断进行检测,结论显示,早期的GPS坐标时间序列中大约有6%的数据为粗差;Mao等[2]及李晓光等[3]采用3倍中误差(3σ)准则进行粗差探测,但3σ准则易受粗差的影响;为增强粗差探测的稳健性,四分位距(interquartile range, IQR)准则得到了更加广泛的应用,其对粗差有一定的抵御能力。IQR准则也衍生出不少新的算法,如经典的最小二乘结合IQR准则的方法(LS-IQR)[4]、抗差1范数结合IQR准则的方法(L1-ModIQR)[5]、数据驱动的奇异谱分析技术结合IQR准则的方法(SSA-IQR)[6]及在频域上与小波分析结合的方法(WA-IQR)[7]等;崔太岷等[8]还提出基于假设检验的方法对观测数据进行粗差探测。近年来,随着人工智能的广泛应用,甚至发展出了利用机器学习和深度学习对各种时间序列进行异常探测的算法[9]。
本文通过检验常用的3σ准则和IQR准则的探测效果,对三维GNSS大地坐标时间序列进行粗差探测,并分析三维方向的探测效果。
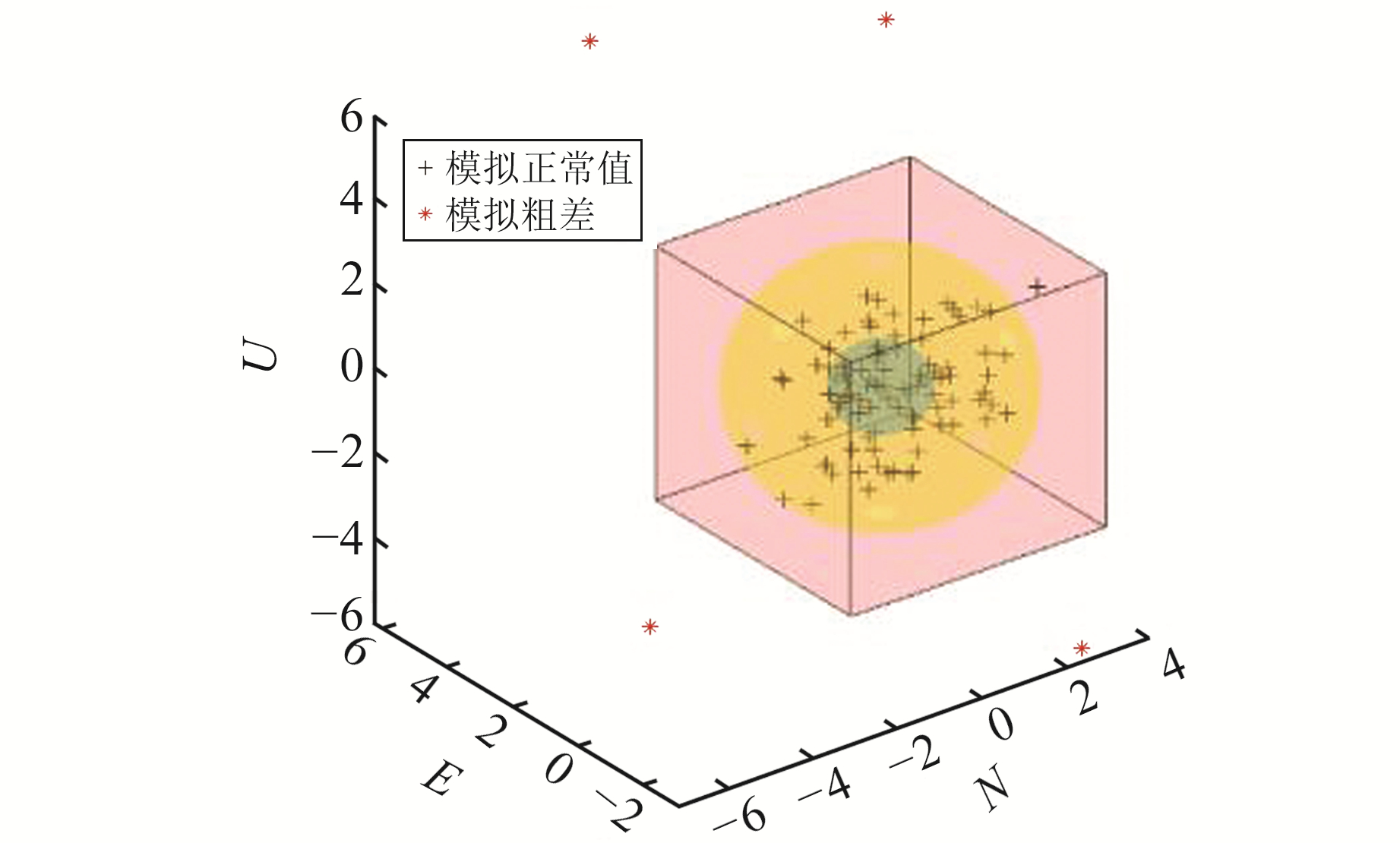
1 GNSS坐标时间序列粗差的特点三维GNSS坐标时间序列的粗差是空间位置的粗差,如图 1(单位mm)所示,假设对某点进行多次GNSS定位,并模拟其中4次定位结果的粗差。
|
图 1 三维GNSS定位 Fig. 1 3D GNSS positioning |
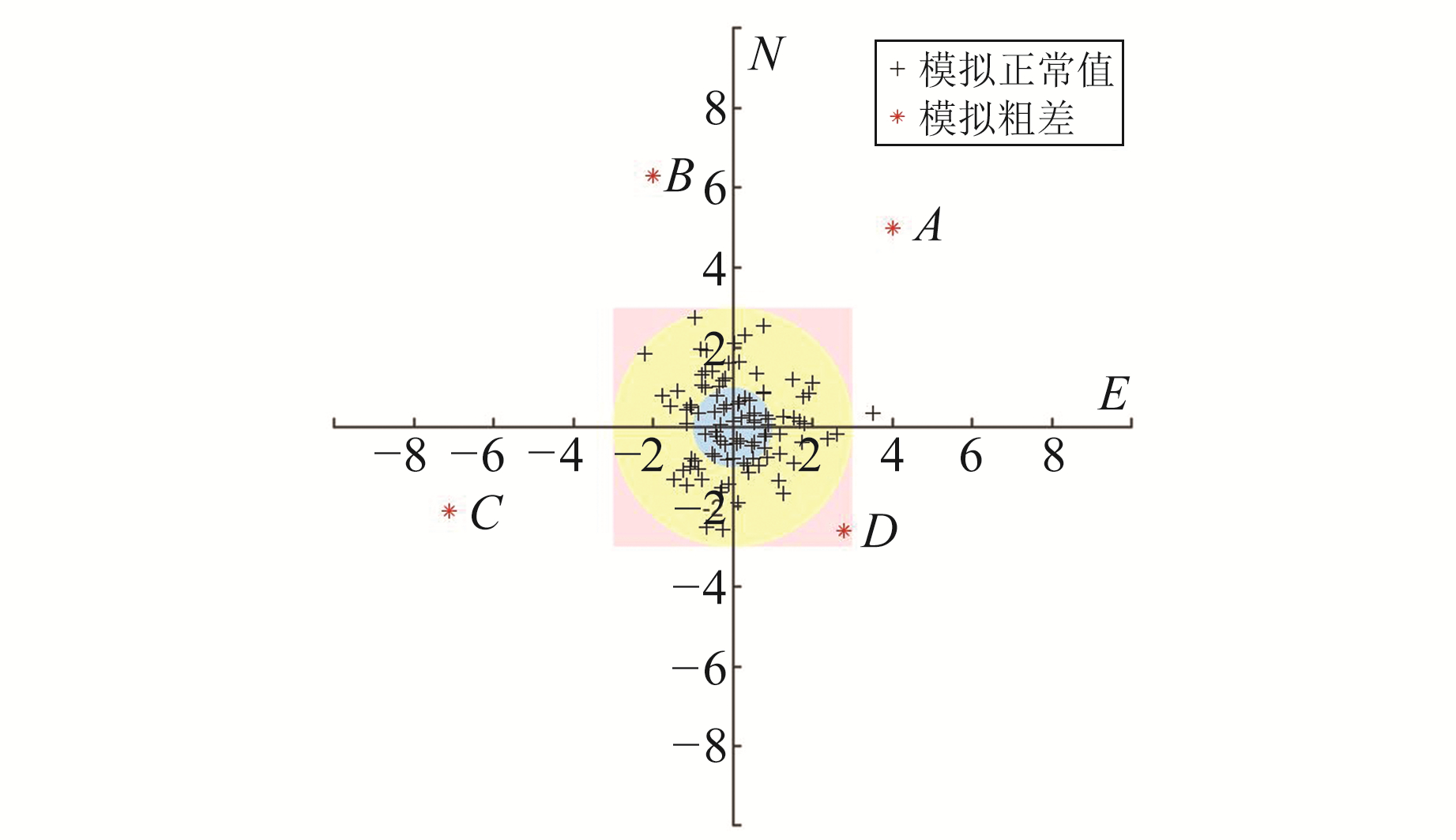
为方便说明,以二维平面坐标为例。假设图 2(单位mm)为GNSS多次测量某点的定位结果,A、B、C、D为4个模拟粗差。
|
图 2 二维GNSS定位 Fig. 2 Horizontal GNSS positioning |
以3σ准则为例,如图 2所示,假设通过平面定位某点100次,N方向和E方向的中误差均为1 mm,并服从正态分布,且分布于3σ之外的数据不大于1%,其中1σ区域为中间淡蓝色区域,3σ为外圈浅黄色区域,浅红色正方形区域为通过N、E方向判定不是粗差而分布于3σ之外的区域。A、B、C、D为4个人为加入的偏离超过3σ的粗差点,如仅考虑N方向,A与B可被识别为粗差,但C与D将不能被正确识别;同样,如果仅考虑E方向,B和D无法被正确探测出来。虽然2个方向的探测均不能识别出在3σ之外的D点,但这样的区域占比很小,仅同时探测N、E方向可大大简化计算量,且不损失过多的探测效率。
类似于平面位置的3σ准则时间序列粗差探测,三维GNSS坐标的粗差探测应探测各个方向的偏差是否大于某个统计量指标,需要求出模型化后三维各方向的统计量信息。但这种处理方法计算复杂,若简化为仅考虑N、E、U三个相互正交方向的偏差,计算量可被大大简化,且能覆盖大多数情形,所以本文采用各个分量分别探测出来的时间并集作为粗差发生历元。
为更有效地检测GNSS坐标时间序列中的粗差,可在时域或频域上对时间序列进行建模,然后针对得到的残差序列进行探测。由于在频域上对时间序列进行分析要求采样均匀[10],但GNSS时间序列中存在不少缺失数据,破坏了其均匀性,进行插值则可能会引入新的粗差。所以,本文分别依据3σ准则和IQR准则,利用迭代最小二乘法求取参数和剔除粗差。
2 综合N、E、U三方向的迭代最小二乘粗差探测方法在实际应用中,时间序列的自相关性随观测历元间隔的增大而降低[11],坐标时间序列中存在与时间相关的有色噪声成分,而且对于跨度较长的坐标时间序列,其前后的年周期和半年周期振幅往往不一样,所以一般采用移动开窗法对粗差进行探测。考虑到GNSS坐标时间序列中的年周期信号最明显[12],所以窗口及步长均设为1 a,不足1 a的数据以离目标数据最近的1 a数据作为探测窗口。
仅靠1次探测在很多情况下不能成功探测出所有粗差,所以在单方向上采取迭代求取参数和剔除粗差的方式。迭代的优势在于可以逐步剔除粗差,并消除粗差对最小二乘法估计参数的影响,最终得到正确的残差序列。而三维粗差探测为N、E、U方向探测出的粗差并集,可大幅降低单方向漏判的概率,具体探测步骤如下:
1) 输入观测方程和权。
2) 利用最小二乘法估计出GNSS时间序列模型,求取参数和残差。
3) 按3σ准则或IQR准则探测和剔除N、E、U方向的粗差。
3σ准则是指当大量GNSS坐标时间序列数据模型化后的残差服从正态分布时,误差分布于±3σ之内的数据占99.73%,所以将分布于3σ之外的数据认为是粗差造成的,其误判比例很小。具体判别式为:
| $ |{\hat v_i}{\rm{ - }}\bar v{\rm{ }}| > 3\sigma $ | (1) |
式中,v为模型化后残差的均值,
而IQR准则将坐标时间序列中的残差序列按大小进行排列,获取其中3个四分位数,IQR统计量为
| $ |{{\hat v}_i} - {{\hat v}_{{\rm{median}}}}| > c \cdot {\rm{IQR}} $ | (2) |
式中,c取值为3,
4) 重复步骤1)~3),直至探测出的粗差个数为0。
5) 求取N、E、U三方向探测所得的粗差并集。
3 算例分析 3.1 模拟数据分析对于单站单方向GNSS坐标时间序列,一般采取式(3)进行建模[10]:
| $ \begin{gathered} y\left(t_{i}\right)=a+b t_{i}+c \sin \left(2 {\rm{ \mathsf{ π} }} t_{i}\right)+d \cos \left(2 {\rm{ \mathsf{ π} }} t_{i}\right)+ \\ e \sin \left(4 {\rm{ \mathsf{ π} }} t_{i}\right)+f \cos \left(4 {\rm{ \mathsf{ π} }} t_{i}\right)+\sum\limits_{j=1}^{n_{j}} g_{i} H\left(t_{i}-T_{h_{j}}\right)+v_{t_{i}} \end{gathered} $ | (3) |
式中,ti为序列的历元,单位a;a对应于截距,其值与预设的初始坐标位置有关;b为站点坐标线速度;c、d和e、f分别为年周期项和半年周期项系数,能够完整描述周期函数的振幅和初始相位;gi为由各种原因引起的阶跃式坐标突变;Thj为阶跃发生的开始时刻;H为阶跃函数,发生突变前H值为0,发生突变后H值为1;vti为观测噪声,可表示成不同噪声模型的组合。
为说明粗差探测方法的有效性并验证三维GNSS坐标时间序列的粗差剔除效果,对模拟数据进行处理。为使问题不过于复杂,又具有一定的代表性,实验根据北京房山(BJFS)站的线速度、周年和半周年振幅模拟了2009~2019年共10 a的三维GNSS坐标时间序列,截距(a)在初始位置N、E、U方向坐标均设为0,加入中误差均为3 mm的白噪声,且不添加阶跃信号,依据式(3)的参数模拟结果如表 1(单位mm)所示。
|
|
表 1 模拟时间序列参数值 Tab. 1 Parameter values of simulated time series |
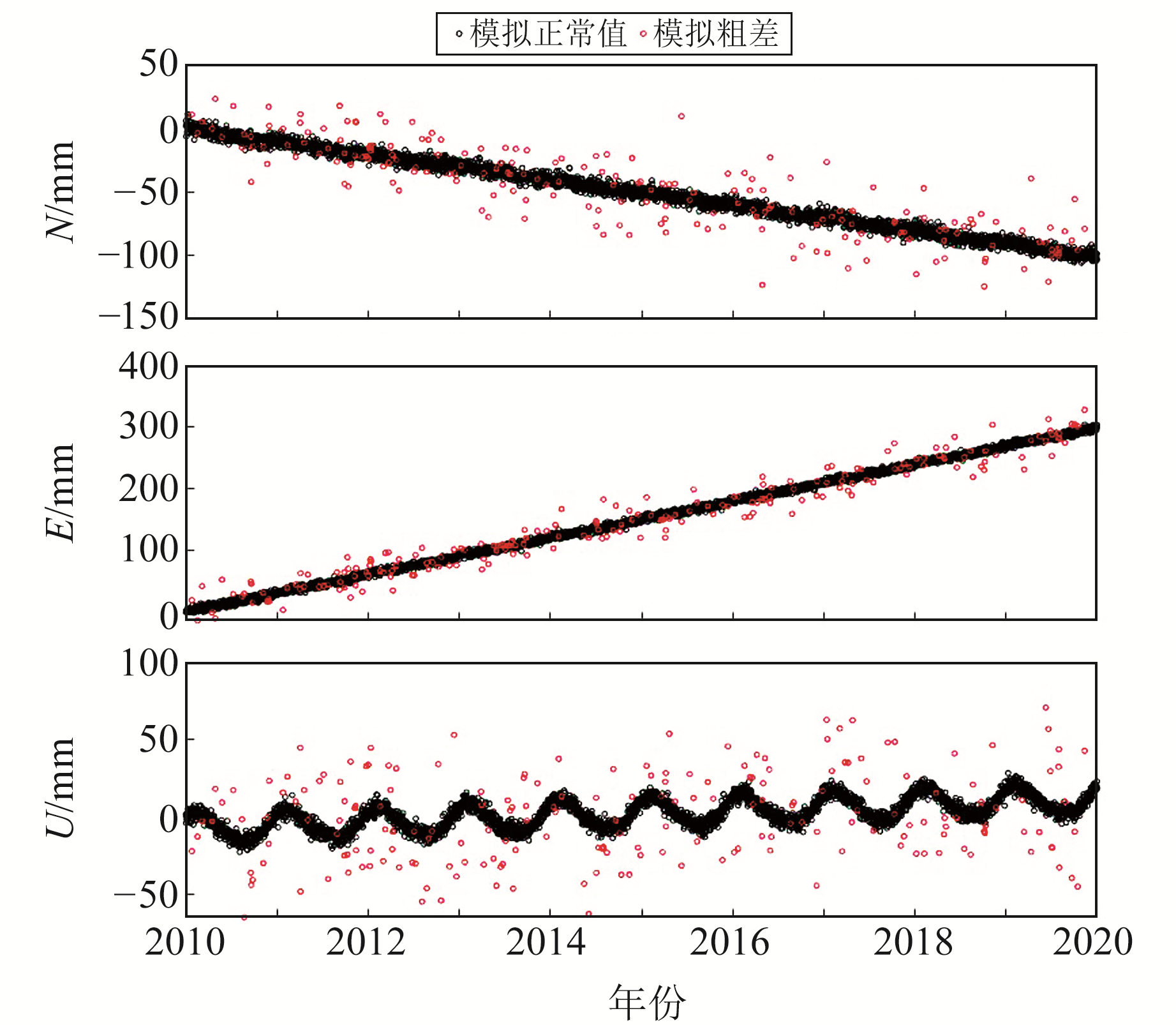
粗差模拟过程如下:1)将三维方向的噪声按照勾股定理求取空间位置误差的模长,将得到的模长放大6倍,并从中随机选取200个大于3倍空间位置误差模长的时间点作为粗差,粗差占比为5.5%。粗差的天顶距φ在0~π中均匀分布,水平方向θ在0~2π中均匀分布。2)将粗差的模长分别乘以cosφ、sinφ·cosθ及sinφ·sinθ,并加入U、N、E方向选取的200个粗差时间点,得到各方向被粗差污染的时间序列。原序列和被粗差污染的序列如图 3所示。
|
图 3 模拟数据及粗差 Fig. 3 Simulatied data and gross errors |
为检验2种准则的检测性能和GNSS三维位置粗差的探测效果,设计模拟实验对2种方案进行对比:1)利用最小二乘结合3σ准则方法(LS-3σ)进行单方向及综合三方向探测;2)利用最小二乘结合IQR准则方法(LS-IQR)进行单方向及综合三方向探测。对比各方法探测的粗差个数和误判个数。
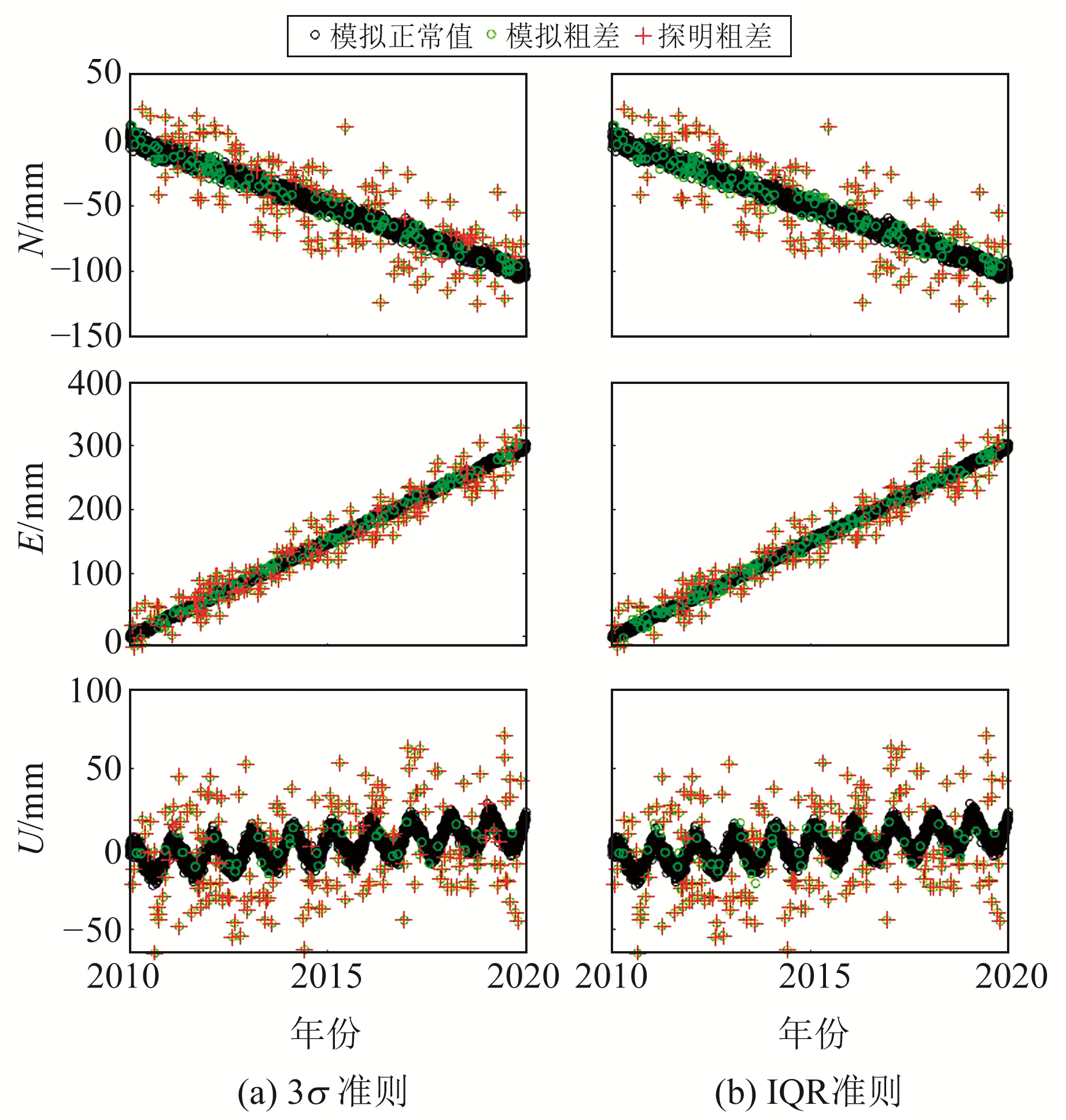
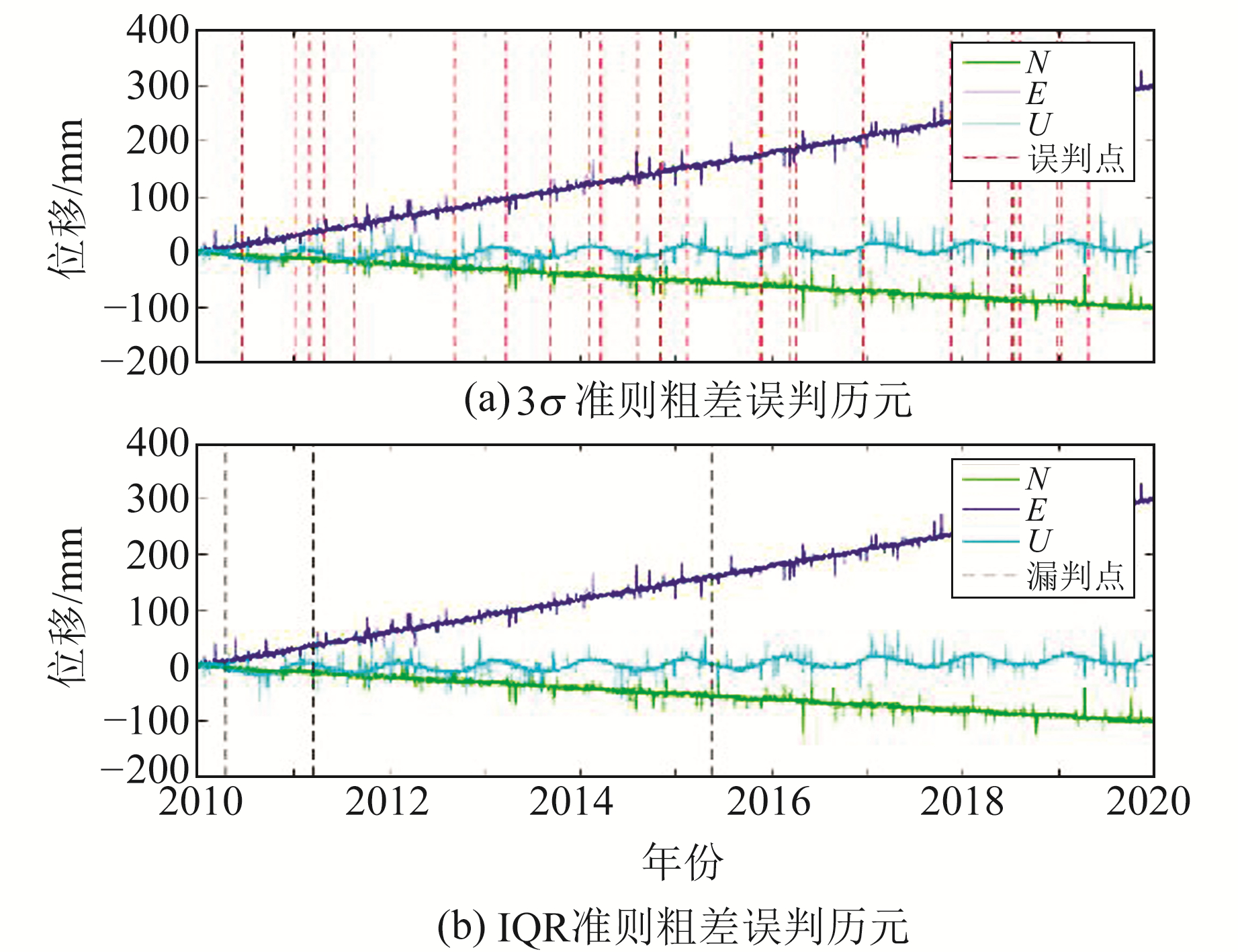
各方案粗差探测结果如表 2所示,3σ准则和IQR准则在各方向的探测结果如图 4所示,综合三方向的探测结果如图 5所示。
|
|
表 2 模拟GNSS坐标时间序列粗差探测效果 Tab. 2 Gross error detection effect of simulated GNSS coordinate time series |
|
图 4 3σ准则与IQR准则各方向粗差探测效果 Fig. 4 3σ criterion and IQR criterion for detection of gross errors in each direction |
|
图 5 3σ准则与IQR准则综合三方向粗差探测误判情况 Fig. 5 Misjudgment by using 3σ and IQR criterion for 3-direction gross error detection |
结合表 2和图 4可以看出,若仅考虑单方向,2种准则均能较好地识别出偏离较大的粗差,但无法识别偏离较小的粗差,所以单方向的探测率均不高。其中,3σ准则水平方向的探测率在55%左右,存在5%左右的误判,而垂直方向的探测率在80%左右,误判率也在5%左右;IQR准则探测率较低,水平方向在45%左右,垂直方向约为75%,不过IQR准则在本次实验中没有出现误判的情况,可认为其误判率显著低于3σ准则。低误判率的主要原因为IQR统计量并未进行标准化,相当于对粗差判定的置信区间进行了压缩。2种方法在垂直方向的探测效率均好于水平方向,主要原因是在粗差的模拟过程中,垂直分量粗差的占比要大于水平分量。将各方向探测得到的粗差求取并集后,3σ准则可探测所有粗差的发生时刻,但误判率也达到了13.5%;IQR准则的探测率超过98%,没有出现误判。图 5中的粗差误判和漏判历元均是在3个方向上的,粗差与模拟正常值没有明显差别。综合来看,IQR准则要好于3σ准则,其以稍低的探测率换取了低误判率。
3.2 实测数据分析根据模拟实验结果,实测数据采用IQR准则进行粗差探测。实测数据为SOPAC(Scrips Orbit and Permanent Array Center)利用GAMIT软件处理的全球参考站坐标时间序列,选取其中9个近年来数据相对完整且稳定的站点作为分析对象,时间跨度为2009.001 4~2018.998 6(2009-01-01~2018-12-31),具体历元数因各站点的数据缺失程度不一而不同。
SOPAC提供4类坐标时间序列:1)仅去除较大粗差的原始序列(raw),即平差前对水平方向偏离大于1 000 mm、垂直方向大于3 000 mm的观测值进行剔除;2)移除了均值、粗差、阶跃的干净时间序列(cleaned trended);3)在干净时间序列的基础上移除趋势的时间序列(cleaned detrended);4)对干净时间序列进行主成分分析滤波得到的过滤时间序列(filtered)。其中,cleaned trended数据的粗差剔除策略是观测值减去计算值(O-C),以检测模型化后的残差是否大于所设置的阈值,其阈值在N、E、U方向分别为25.0 mm、25.0 mm和35.0 mm。
本文对SOPAC提供的raw数据进行粗差探测,并与提供的cleaned trended数据进行对比来进行验证。为保证模型的一致性,在进行粗差探测前,通过查询cleaned trended数据中的阶跃信息进行模型改正,再利用IQR准则对时间序列的三方向进行粗差探测,并求得并集,探测结果见表 3。由表 3可知,每个测站都存在数据缺失的情况,缺失比例在2%~32%,不满足均匀采样的条件,表明实测的IGS站原始序列数据不适合直接在频域上进行分析。利用本文方法对9个IGS站数据进行粗差探测得出,原始坐标时间序列中含有的粗差占比在0.1%~4.7%之间。
|
|
表 3 IGS参考站粗差探测效果 Tab. 3 Gross error detection effect of IGS stations |
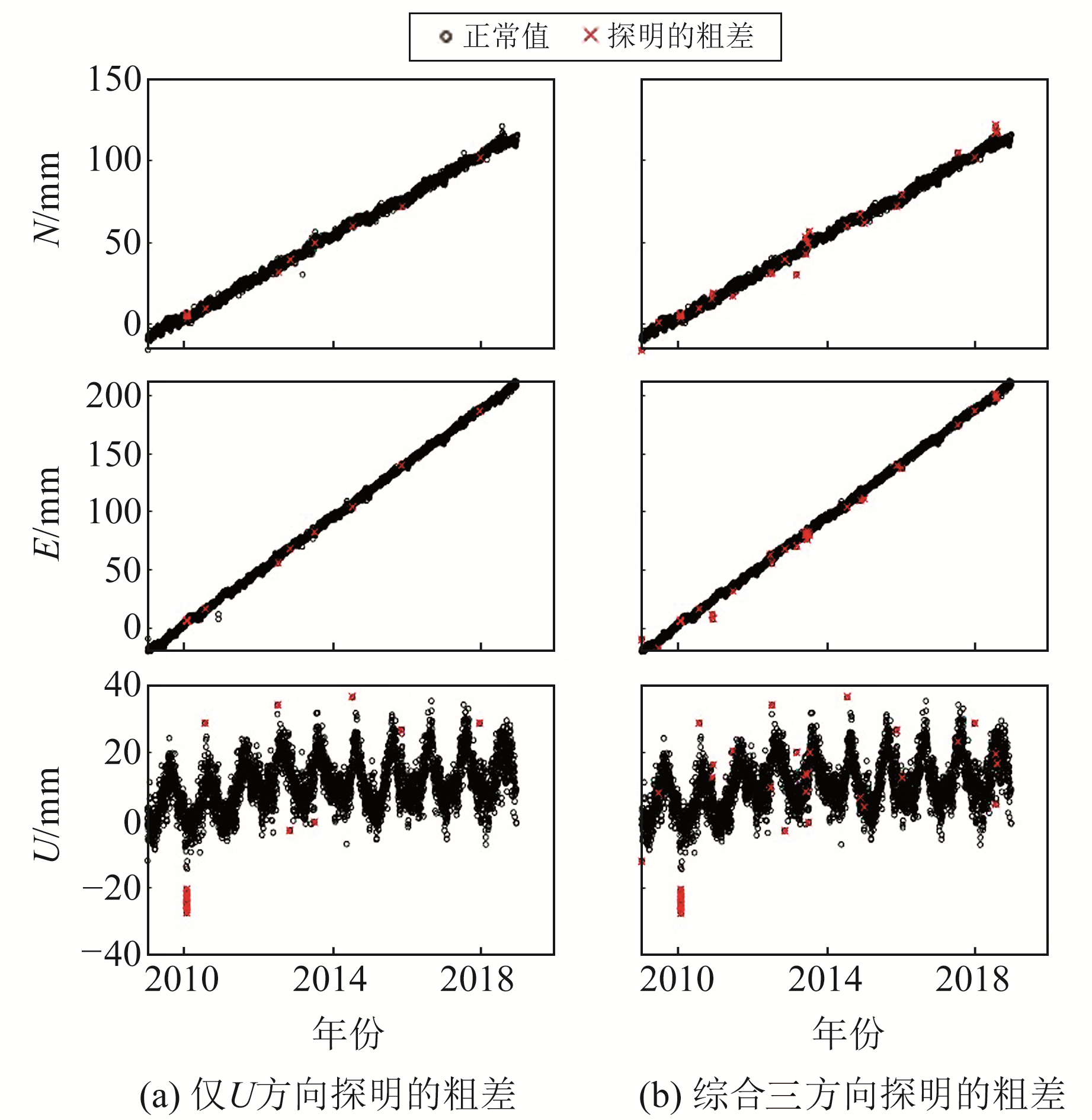
为详细说明探测效果,以BUCU站为例,对其三维位置粗差探测效果进行分析,检验探测结果的有效性,如图 6所示。可以看出:
|
图 6 BUCU站粗差探测效果 Fig. 6 Gross error detection effect at BUCU station |
1) 由于水平方向存在非常明显的线性趋势,局部特征容易被线性趋势掩盖,仅靠目测不易判断其中存在的粗差。在仅考虑垂直方向的情况下,2个水平方向的明显粗差未能被识别出来。综合探测3个方向后,识别的粗差个数明显增多,包括很多从图上看起来不像粗差的值。
2) 根据模拟实验的结果,在多个方向上同时探测出某个历元存在粗差的比例大概在70%左右,而BUCU站的实测数据中仅有10%左右,说明存在不小比例的误判。其原因可能是存在一些未探明的阶跃信号,如2010.053 4~2010.072 6连续8 d被标记为粗差,通过检查N方向数据发现,其很有可能是某种类型的阶跃,表明在cleaned trend数据中还存在没有被探明的阶跃。
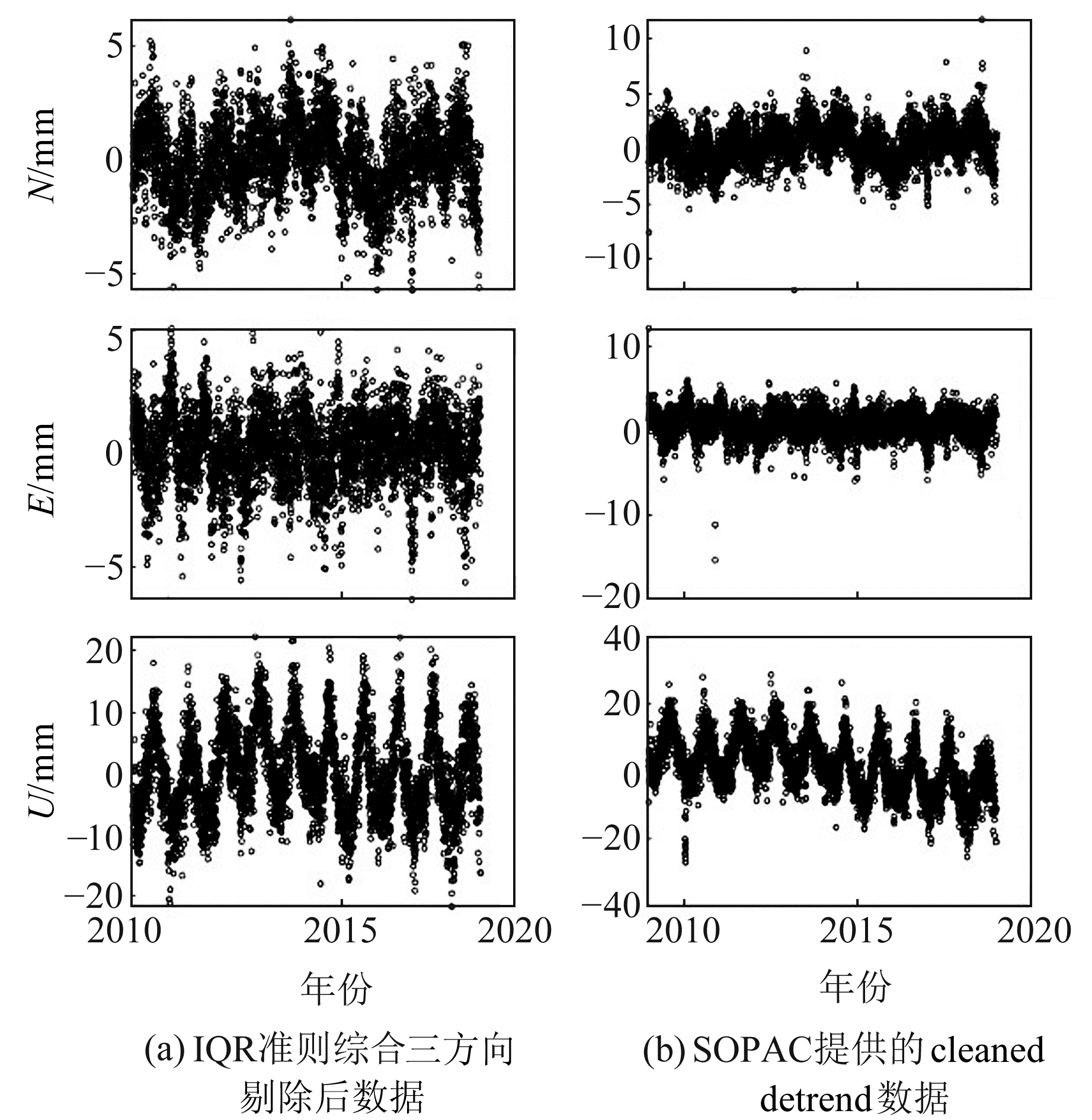
3) 坐标时间序列中的噪声并不是单纯的白噪声,其先验随机模型不准确,导致其与模拟实验结果存在差异。为更明显地对粗差剔除效果进行对比,实验通过最小二乘法估计出利用IQR准则剔除粗差后序列的趋势及截距,将得到的去趋势数据与SOPAC提供的cleaned detrend数据进行对比,结果如图 7所示。从图 7可以看出,相比于cleaned detrend数据,IQR准则综合三方向剔除粗差后的时间序列不仅剔除了孤立的异常点,细节特征也更加明显。
|
图 7 IQR准则综合三方向剔除粗差后时间序列与cleaned detrend时间序列对比 Fig. 7 Comparison between time series after gross error elimination by IQR criterion and cleaned detrend time series |
本文对比了最小二乘分别结合3σ准则和IQR准则对三维GNSS坐标时间序列进行粗差探测的方法。由模拟实验结果可见,综合三方向的探测结果明显好于仅考虑单方向的结果;3σ准则的探测效率高,但存在较多的误判;IQR准则探测效率略低,但没有出现误判的情况。总体来看,IQR准则要好于3σ准则。
然而实测数据情况要更为复杂,其中含有大量的阶跃信号,如果未准确建模,将会对参数估计产生很大影响,进而影响探测效果。而在SOPAC提供的干净时间序列中依然存在很多没有被探明的阶跃,造成了探测中粗差与阶跃的混淆,因此将阶跃和粗差进行区分十分重要。
另外,GNSS坐标时间序列中的噪声成分复杂,其随机模型不准确会使参数估值和残差的计算受到很大影响,进而影响粗差探测的效果。获取更加准确的函数模型和随机模型也有助于提高粗差探测的准确性。
GNSS坐标时间序列中粗差产生的原因常被笼统地归结为仪器故障或测量条件的限制,对粗差产生的原因进行定性和定量分析,有助于在利用GNSS观测数据获取坐标时间序列阶段避免或减弱粗差的影响。
| [1] |
Perfetti N. Detection of Station Coordinate Discontinuities within the Italian GPS Fiducial Network[J]. Journal of Geodesy, 2006, 80(7): 381-396 DOI:10.1007/s00190-006-0080-6
(  0) 0) |
| [2] |
Mao A, Harrison C G A, Dixon T H. Noise in GPS Coordinate Time Series[J]. Journal of Geophysical Research: Earth Surface, 1999, 104(B2): 2 797-2 816 DOI:10.1029/1998JB900033
(  0) 0) |
| [3] |
李晓光, 程鹏飞, 成英燕. GPS周解坐标时间序列粗差剔除的策略分析[J]. 测绘科学, 2018, 43(3): 1-5 (Li Xiaoguang, Cheng Pengfei, Cheng Yingyan. Gross Error Elimination Strategy Analysis Based on GPS Weekly Coordinates Time Series[J]. Science of Surveying and Mapping, 2018, 43(3): 1-5)
(  0) 0) |
| [4] |
Nikolaidis R. Observation of Global and Seismic Deformation with the Global Positioning System[D]. San Diego: University of California, 2002
(  0) 0) |
| [5] |
明锋, 曾安敏, 景一帆. L1范数与IQR统计量组合的GNSS坐标序列粗差探测算法[J]. 测绘科学技术学报, 2016, 33(2): 127-132 (Ming Feng, Zeng Anmin, Jing Yifan. A New Method of Outlier Detection for GNSS Position Time Series Based on the Combination of L1-Norm and IQR Statistic[J]. Journal of Geomatics Science and Technology, 2016, 33(2): 127-132)
(  0) 0) |
| [6] |
Wang X, Cheng Y, Wu S, et al. An Effective Toolkit for the Interpolation and Gross Error Detection of GPS Time Series[J]. Empire Survey Review, 2015, 48(348): 202-211
(  0) 0) |
| [7] |
Ji K P, Shen Y Z. A Wavelet-Based Outlier Detection and Noise Component Analysis for GNSS Position Time Series[C]. International Association of Geodesy Symposia, Berlin, 2020
(  0) 0) |
| [8] |
崔太岷, 郭党伍, 王俊雷, 等. 基于Score检验统计的粗差探测法[J]. 测绘通报, 2019(增1): 195-198 (Cui Taimin, Guo Dangwu, Wang Junlei, et al. Gross Error Detection Based on Score Test Statistics[J]. Bulletin of Surveying and Mapping, 2019(S1): 195-198)
(  0) 0) |
| [9] |
Maya S, Ueno K, Nishikawa T. dLSTM: A New Approach for Anomaly Detection Using Deep Learning with Delayed Prediction[J]. International Journal of Data Science and Analytics, 2019, 8(2): 137-164 DOI:10.1007/s41060-019-00186-0
(  0) 0) |
| [10] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496-503)
(  0) 0) |
| [11] |
徐天河, 贺凯飞. 移动开窗检验法及其在GOCE数据粗差探测中的应用[J]. 测绘学报, 2009, 38(5): 391-396 (Xu Tianhe, He Kaifei. Outlier Snooping Based on the Test Statistic of Moving Windows and Its Applications in GOCE Data Preprocessing[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 391-396 DOI:10.3321/j.issn:1001-1595.2009.05.003)
(  0) 0) |
| [12] |
田云锋. GPS位置时间序列中的中长期误差研究[D]. 北京: 中国地震局地质研究所, 2011 (Tian Yunfeng. Study on Intermediate and Long-Term Errors in GPS Position Time Series[D]. Beijing: Institute of Geology, CEA, 2011)
(  0) 0) |
| [13] |
武曙光. 区域CORS站坐标时间序列特征分析[D]. 武汉: 武汉大学, 2017 (Wu Shuguang. Characteristics of Coordinate Time Series from Regional CORS Stations[D]. Wuhan: Wuhan University, 2017)
(  0) 0) |
2. 96712 Troops of PLA, Jingdezhen 333300, China;
3. Institute of Space Science and Applied Technology, Harbin Institute of Technology, Shenzhen, 6 First-Pingshan Road, Shenzhen 518055, China;
4. 61206 Troops of PLA, Beijing 100042, China;
5. 96711 Troops of PLA, Chizhou 247100, China
 2021, Vol. 41
2021, Vol. 41

