采用GNSS获取载体平台的姿态信息具有安装容易、成本低、精度不随时间变化等优点,已在海上科研、空中摄影测量、陆地导航及地震学等领域得到广泛应用[1-4]。现有的GNSS测姿方法可分为单天线测姿和多天线测姿[5],相较于多天线测姿,单天线测姿原理简单,且对载体平台大小要求不高,不需要增加额外的天线即可完成定姿,可进一步控制测量仪器的成本。目前,关于单天线测姿的研究主要是将其与陀螺仪、惯性导航系统、电子罗盘等传感器进行组合[5-7],而对单一的单天线测姿在陆地导航中的应用及精度分析研究较少。本文首先介绍单天线GNSS测姿的数学模型,然后分析其主要的误差来源,最后采用车载实测数据进行姿态解算,将解算结果与高精度惯导结果相比较,并从测速精度和载体运动状态2个方面对姿态结果进行精度分析与评估。
1 单天线测姿基本原理在姿态测量中,姿态参数反映的是载体坐标系与参考坐标系(即地理坐标系)之间的旋转关系,而采用GNSS单天线测姿获得的伪姿态反映的是载体速度坐标系与参考坐标系之间的旋转关系。在陆地导航中,载体处于协调运动状态,侧滑角为0,速度坐标系与载体坐标系之间的差别较小,可将伪姿态作为标准姿态。单天线测姿的基础是载体的速度测量,通常采用多普勒测速法获得载体速度,GNSS单站测速的观测方程为:
| $ \lambda D = \dot \rho + c{{\dot t}_{\rm{r}}} - c{{\dot t}^{\rm{j}}} + \dot T - \dot I + \dot \varepsilon $ | (1) |
式中,λ为载波相位波长,D为多普勒观测值,
姿态参数可用3个欧拉角来表示,伪姿态中将航向角定义为速度矢量在水平面上的投影与地理坐标系正北方向之间的夹角,将俯仰角定义为速度矢量与水平面之间的夹角。根据定义,航向角及俯仰角可由地理坐标系中的速度矢量通过式(2)、式(3)计算得到:
| $\begin{aligned} &y=\left\{\begin{array}{l} \arctan \left(v_{E} / v_{N}\right), v_{E}>0, v_{N}>0 \\ \pi+\arctan \left(v_{E} / v_{N}\right), v_{N}<0 \\ 2 \pi+\arctan \left(v_{E} / v_{N}\right), v_{E}<0, v_{N}>0 \end{array}\right. \end{aligned} $ | (2) |
| $p=\arctan \left(v_{U} / \sqrt{\left(v_{E}\right)^{2}+\left(v_{N}\right)^{2}}\right) $ | (3) |
式中,vE、vN、vU分别为地理坐标系下东西、南北、垂直3个方向上的速度分量。从式(2)可看出,航向角的表达式为反正切函数,为了避免计算结果出现多值问题,采用速度分量符号来判定航向角的象限[8]。横滚角r由加速度求出:
| $ r = {\rm{arcsin}}\left[ {\left( {l \times p} \right)/\left( {\left| l \right| \times |p|} \right)} \right] $ | (4) |
式中,l=an-gn, p=g×v,an、gn分别由载体加速度和重力加速度沿载体速度法线方向分解得到。
2 GNSS单天线测姿误差分析采用单天线进行姿态测量的误差主要分为3类: 1)与载体速度相关的误差,分为载体速度测量误差和速度大小引起的姿态误差;2)与天线相关的误差,主要包括天线安置偏差和接收机天线相位中心偏差;3)载体运动环境引起的误差,主要有多路径误差及载体运动路况引起的误差。在陆地导航中,横滚角无明显变化,因此不对其进行分析。本文以式(2)和式(3)为基础,分析各项误差对航向角和俯仰角的影响。
2.1 速度相关误差根据单天线GNSS测姿原理,可由测速精度推出航向角和俯仰角的精度。以航向角为例,对式(2)进行求导,得到航向角微分方程为:
| $ {\delta _y} = \frac{{{v_N}{\delta _{{V_E}}} - {v_E}{\delta _{{V_N}}}}}{{v_E^2 + v_N^2}} $ | (5) |
对式(5)运用误差传播定律,忽略各坐标分量之间的相关性,可求得航向角的中误差σy为:
| $ \sigma_{y}=\frac{\sqrt{v_{N}^{2} \sigma_{v_{E}}^{2}+v_{E}^{2} \sigma_{v_{N}}^{2}}}{v_{E}^{2}+v_{N}^{2}} \approx \frac{\sigma_{v_{H}}}{v_{H}} $ | (6) |
式中,vH为载体在地理坐标系中的水平方向速度,σvE、σvN分别为载体速度在东西、南北2个方向上的误差,σvH为速度在水平方向上的误差。同理可得俯仰角中误差σp为:
| $\sigma_{p}=\frac{\sqrt{\left(v_{E}^{2}+v_{N}^{2}\right)^{2} \sigma_{v_{U}}^{2}+v_{E}^{2} v_{U}^{2} \sigma_{v_{E}}^{2}+v_{N}^{2} v_{U}^{2} \sigma_{v_{N}}^{2}}}{\left(v_{E}^{2}+v_{N}^{2}+v_{U}^{2}\right) \sqrt{v_{E}^{2}+v_{N}^{2}}} $ | (7) |
进一步简化可得:
| $ {\sigma _p} \approx \frac{{\sqrt {v_H^2\sigma _{{v_U}}^2 + v_U^2\sigma _{{v_H}}^2} }}{{v_{ENU}^2}} $ | (8) |
式中,σvU为载体速度在天顶方向上的测量误差。由式(6)可知,当载体的速度一定时,航向角的误差只与水平方向上的速度误差相关,对于低速载体,误差传播系数较大,测速误差对姿态结果精度的影响不可忽略。同理,俯仰角的精度主要受水平方向和垂直方向速度误差的影响。由式(6)和式(7)可知,姿态结果还受载体速度大小的影响,速度越小误差水平越高,当载体处于静止状态时误差达到最大,此时解算出的姿态结果不可用,可采用前一历元的姿态来表示当前姿态[9]。
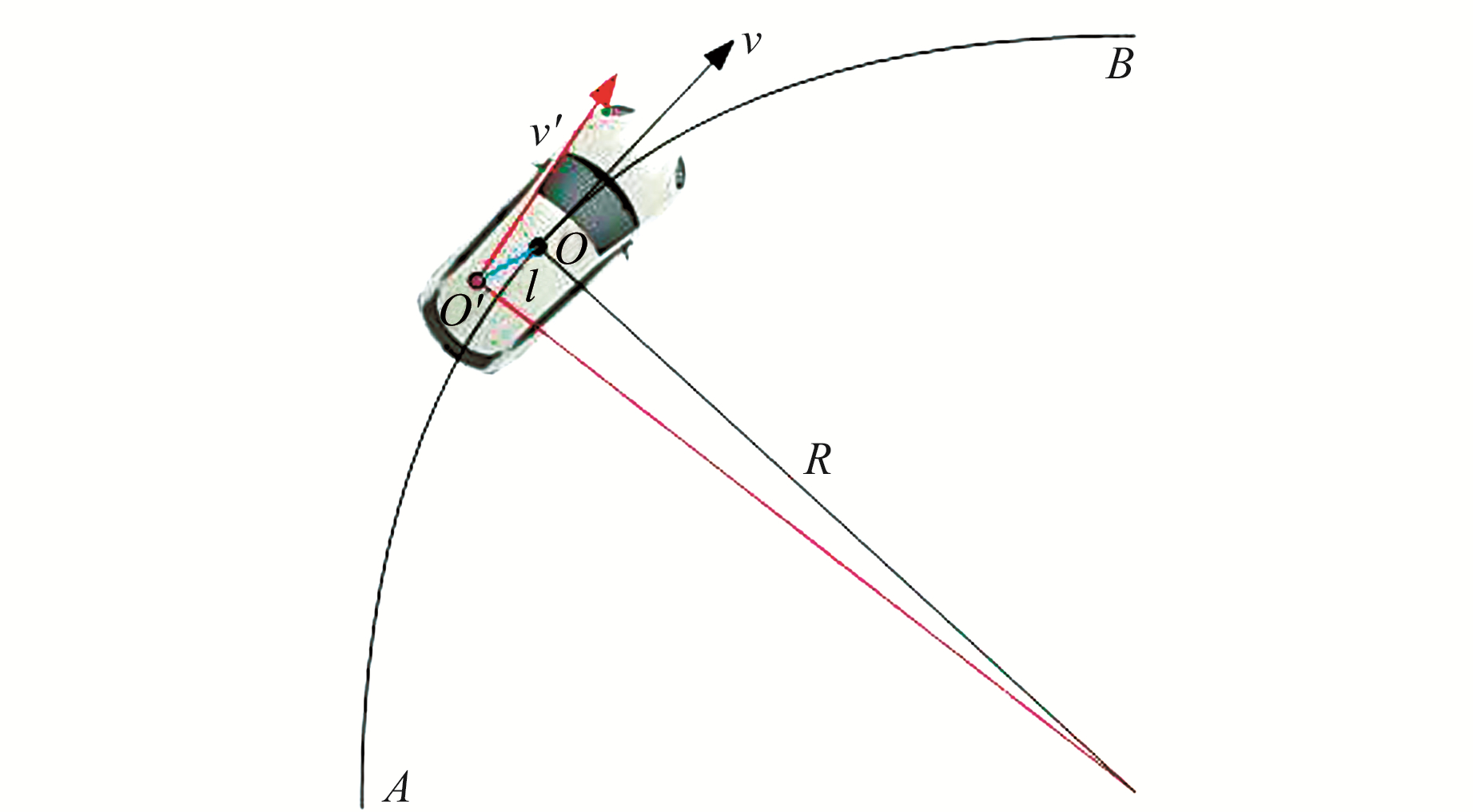
2.2 天线相关误差根据定义,载体坐标系原点为载体质心,故计算姿态采用的速度应为载体质心速度,但实际上由于载体形状等条件的限制及天线自身的相位中心偏差,天线相位中心无法准确与载体质心重合,导致求出的天线相位中心速度与质心速度存在偏差。如图 1所示,O为载体质心,O′为天线相位中心,两点之间的距离为l。假设载体质心沿曲率为1/R的弧段AB作转向运动,在某一时刻,载体质心的速度为v,天线相位中心的速度为v′, 则2个速度矢量之间的夹角α可近似表示为:
| $ \alpha \approx {\rm{arctan}}\left( {l/R} \right) $ | (9) |
|
图 1 天线位置偏差引起的速度误差 Fig. 1 Velocity error caused by antenna position deviation |
由式(9)可知,载体在行驶过程中,速度偏差角只与路径曲率相关,曲率越大偏差角越大。当曲率为0时,2个速度矢量平行,姿态结果不受天线安置偏差的影响。
2.3 运动环境引起的误差当载体在复杂环境中运动时,由环境因素引起的多路径效应会直接影响姿态结果精度[10]。在信号遮挡严重的路段,无法进行姿态解算,同时载体运动路况也会对姿态造成影响,在雨雪天气,路面湿滑,载体容易发生侧滑现象,此时速度坐标系与载体坐标系之间的偏差不可忽略。
3 实验测试及结果分析为验证GNSS单天线测姿算法在低动态载体应用中的精度和可靠性,进行车载测试。在车顶安置接收机天线,并使用高精度惯导输出的姿态结果作为参考真值,实验车速在14~26 m/s范围内变化。采集到的数据使用自编程序GNSS姿态解算系统进行处理,获得航向角与俯仰角,并对其精度进行分析。
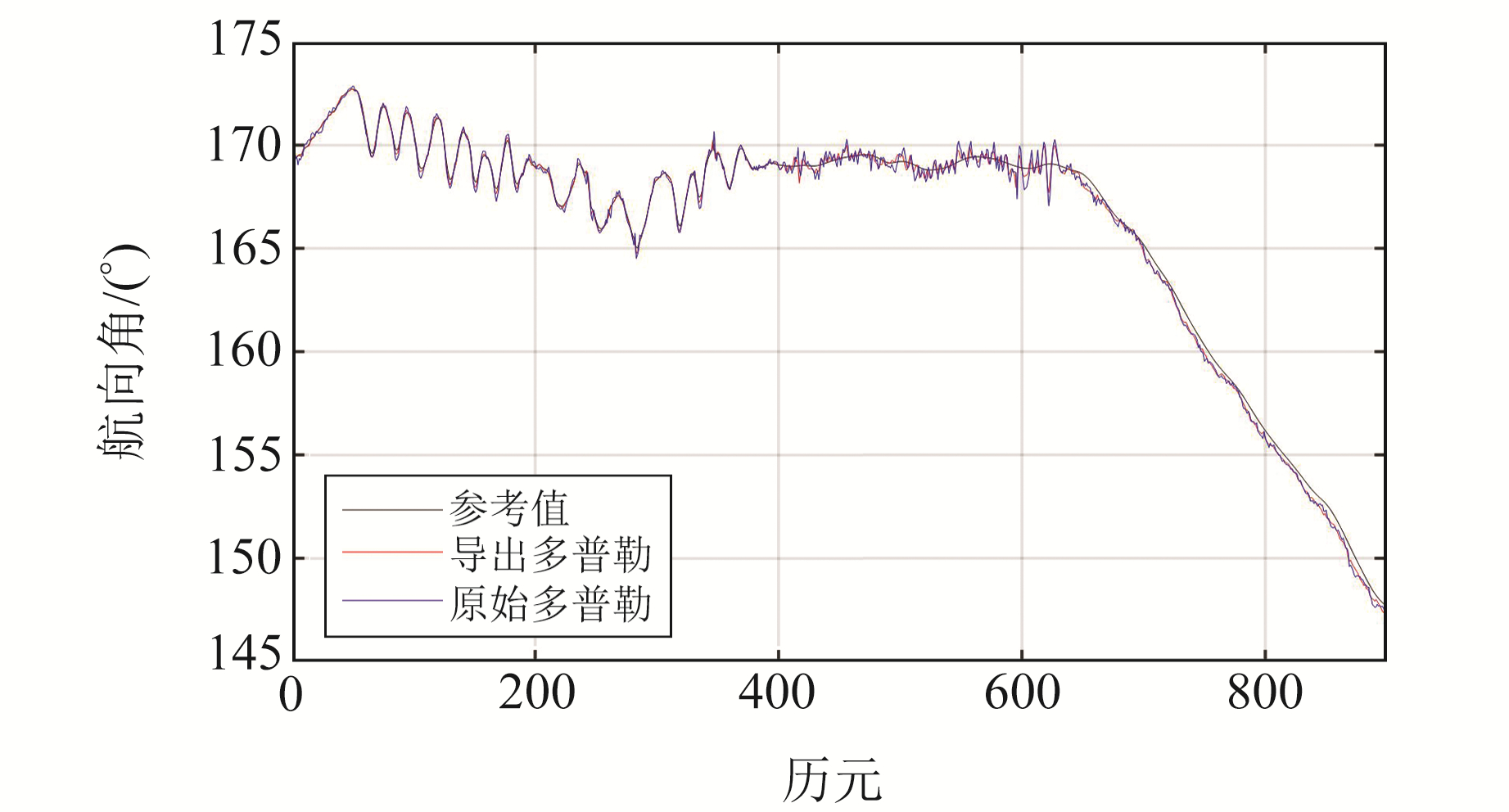
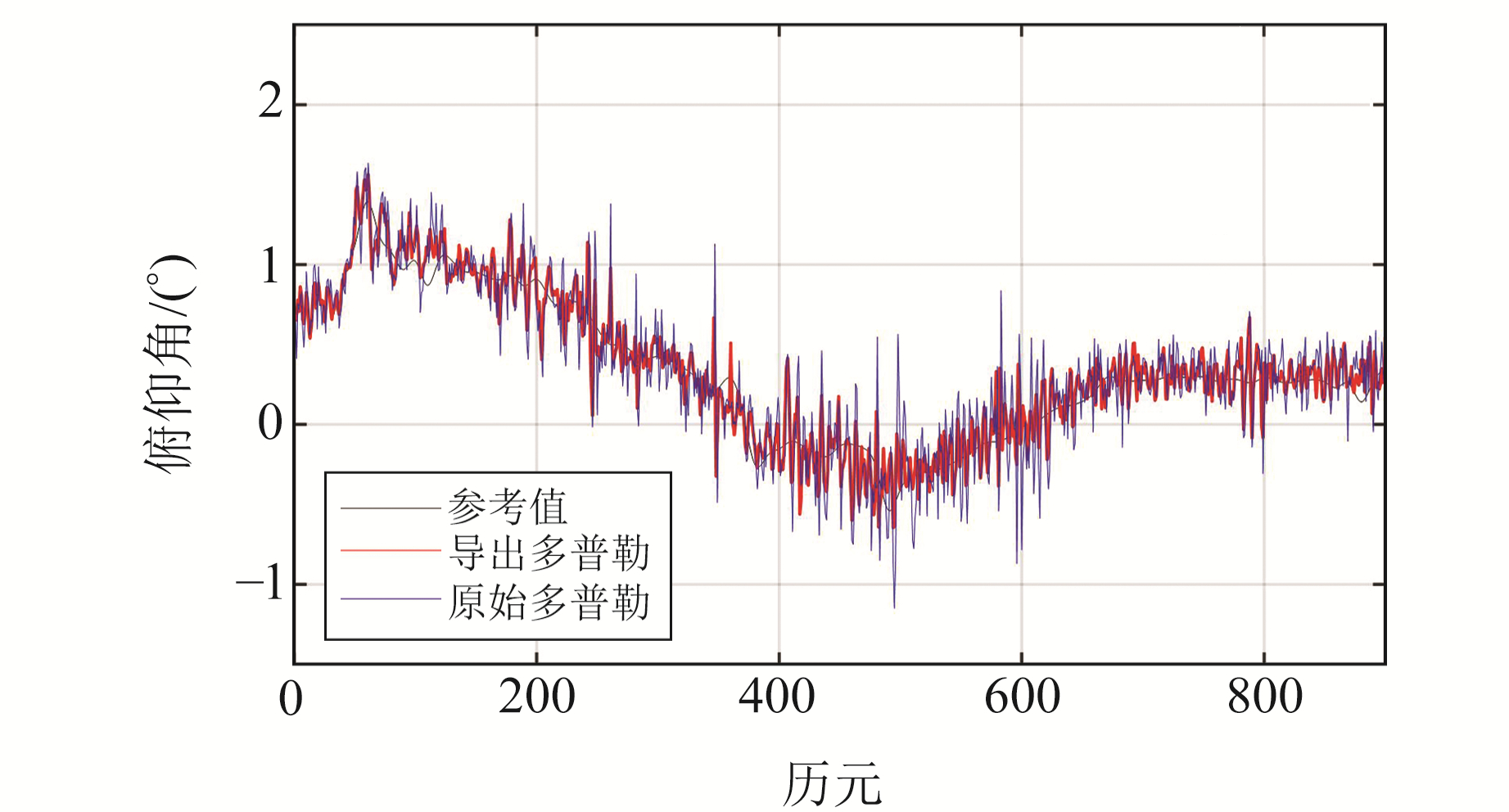
3.1 速度测量误差影响多普勒观测值分为原始多普勒观测值和载波相位导出多普勒观测值,由于观测噪声等因素的影响,载波相位导出多普勒观测值的测速精度高于原始多普勒观测值[11]。为验证不同测速精度对载体姿态结果的影响,分别采用2种多普勒观测值解算载体速度,再通过速度矢量计算出载体的姿态,得到的航向角及俯仰角随时间的变化见图 2和3。
|
图 2 航向角变化 Fig. 2 Changes of heading angle |
|
图 3 俯仰角变化 Fig. 3 Changes of pitch angle |
由图 2和3可知,采用载波相位导出多普勒观测值和原始多普勒观测值解算的姿态结果均在参考值上下波动,其中俯仰角的变化范围为[-1°, 1.5°],航向角的变化范围为[173°, 147°],测姿结果准确反映了载体姿态的变化情况,验证了单天线姿态测量在陆地载体上的可用性。
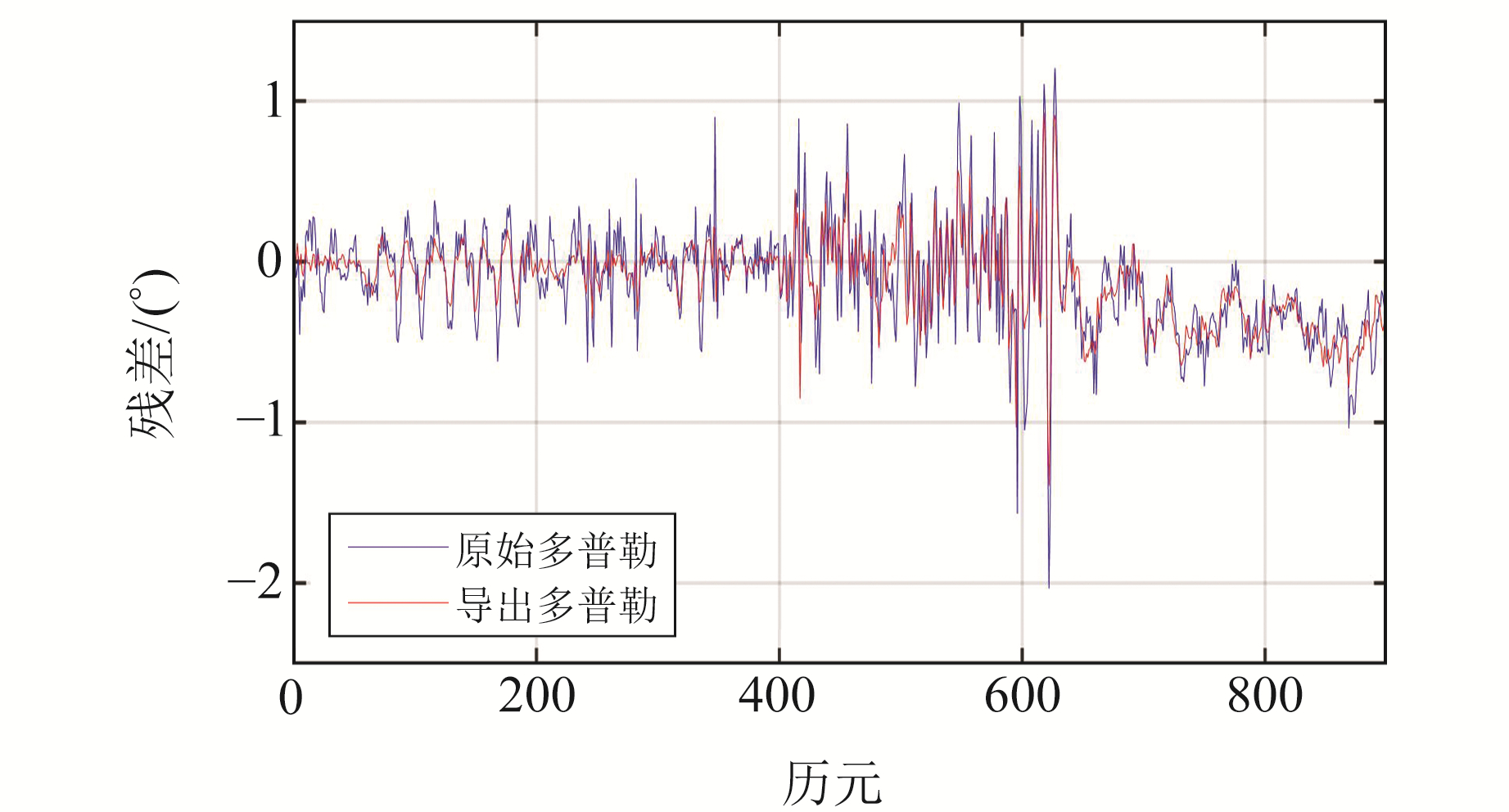
将解得的姿态结果与参考值进行比较,结果如图 4、5和表 1、2所示。
|
图 4 航向角残差序列 Fig. 4 The residual sequence of heading angle |
|
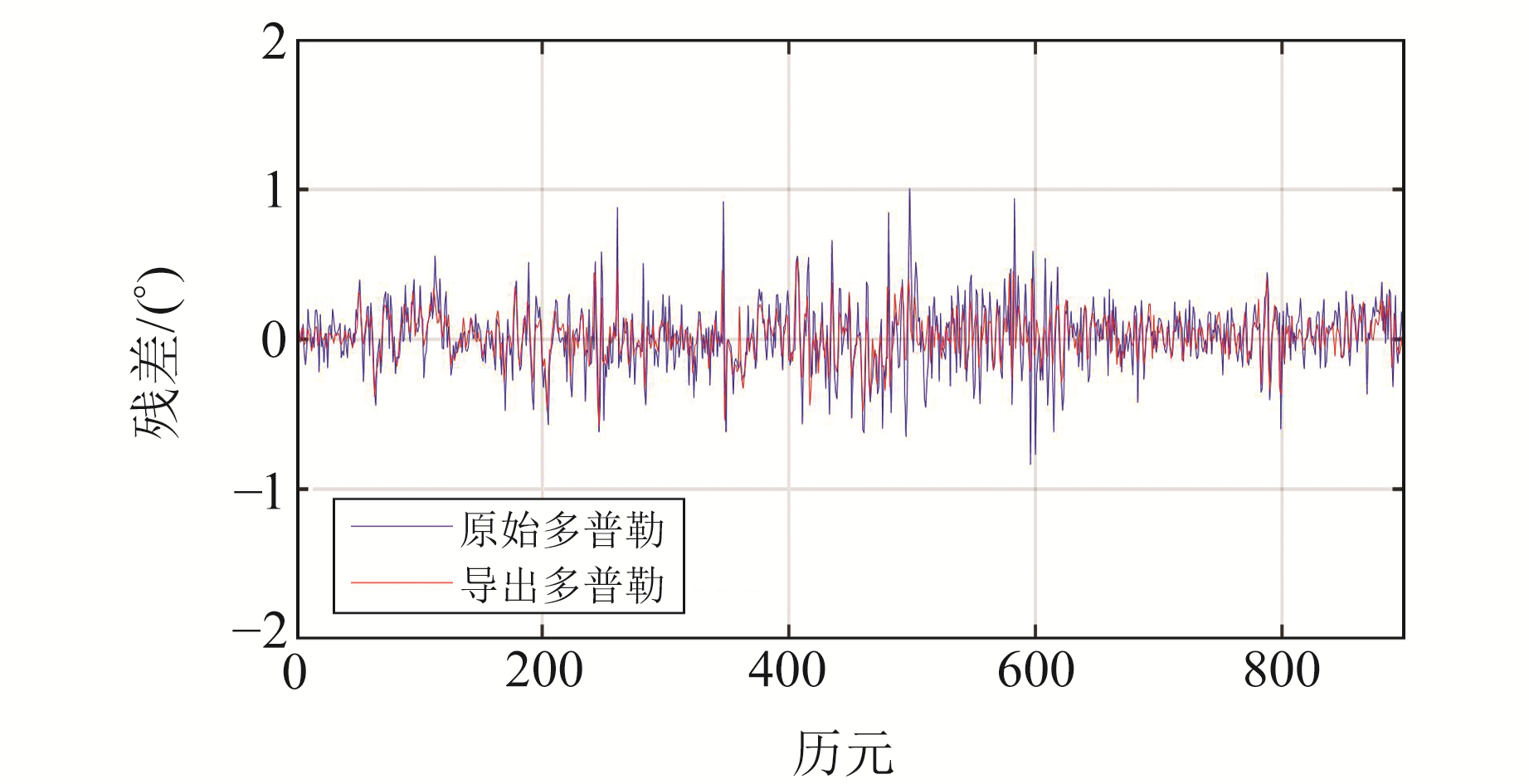
图 5 俯仰角残差序列 Fig. 5 The residual sequence of pitch angle |
|
|
表 1 不同速度精度对航向角影响统计 Tab. 1 Influence on heading angle by different speed accuracy |
|
|
表 2 不同速度精度对俯仰角影响统计 Tab. 2 Influence on pitch angle by different speed accuracy |
由上述结果可得,采用载波相位导出多普勒观测值进行姿态解算时,航向角和俯仰角的均方根误差分别为0.277°和0.144°,误差平均值分别为-0.118°和0.021°;原始多普勒观测值解算的航向角和俯仰角均方根误差分别为0.35°和0.22°,误差平均值分别为-0.120°和0.017°。可以看出,通过载波相位导出多普勒观测值计算的姿态结果相较于原始多普勒观测值更稳定,主要有2个原因:1)采用原始多普勒观测值解算的是载体的瞬时速度,利用载波相位导出多普勒观测值获得的是观测历元间的平均速度,平均速度相较于瞬时速度更平滑;2)原始多普勒观测值的噪声等级大于载波相位导出多普勒观测值。
实验证明,在陆地低动态载体中,GNSS单天线测姿结果易受测速精度的影响。
3.2 天线位置偏差影响根据式(6)和式(7)可知,在仅考虑速度测量误差的情况下,由于垂直方向的测速精度较低,测出的航向角精度应高于俯仰角,但对实验结果进行分析后发现,航向角误差大于俯仰角。考虑到可能是由天线偏差引起的,分别对载体直行和转向状态时的航向角进行分析,结果如图 6所示。

|
图 6 不同运动状态下航向角的误差比对 Fig. 6 The error of heading angle under different motion states |
由图 6可以看出,载体在直行时的航向角误差小于转向时的航向角误差,进一步计算不同运动状态下的航向角误差,结果如表 3所示。
|
|
表 3 不同运动状态下航向角的误差统计 Tab. 3 Error of heading angleunder different motion states |
由上述结果可知,载体在直行和转向状态下,航向角的均方根误差分别为0.153°和0.815°,误差平均值分别为-0.004°和0.681°,转向时航向角的最大误差为2.141°,大于直行状态下航向角的误差绝对值。导致这一结果的原因主要有:1)天线相位中心与载体质心不重合,车辆在进行转向时,天线相位中心速度与载体质心速度存在偏差,而在直行状态下,两者基本一致;2)载体在转向过程中会减慢速度,式(6)中的误差传播系数会增大,导致速度测量误差变大。综合上述原因可知,在陆地导航中,由于载体在水平方向的方位变化大于垂直方向,因此由GNSS单天线求出的俯仰角精度高于航向角。
4 结语本文介绍了GNSS单天线测姿的数学模型,主要分析了载体速度误差、天线位置偏差等误差对测姿结果的影响。通过车载实验验证了单天线姿态测量在低动态载体中的可用性,并比较了不同测速精度对测姿结果的影响。实验表明,在陆地低动态载体中,航向角及俯仰角的RMS值均在1°以内。根据误差分析结果,在使用GNSS单天线进行姿态测量时,要尽量将天线安置在载体质心位置,并避免在信号遮挡严重的环境进行作业。GNSS单天线测姿算法可应用于低速运动且姿态变化较小的载体,并且具有很大的应用空间和经济价值。
| [1] |
Teunissen P J G, Giorgi G, Buist P J. Testing of a New Single-Frequency GNSS Carrier Phase Attitude Determination Method: Land, Ship and Aircraft Experiments[J]. GPS Solutions, 2011, 15(1): 15-28 DOI:10.1007/s10291-010-0164-x
(  0) 0) |
| [2] |
Zhen D. On GPS Based Attitude Determination[D]. North Rhine-Westphalia: University of Siegen, 2013
(  0) 0) |
| [3] |
Lu G. Development of a GPS Multi-Antenna System for Attitude Determination[D]. Calgary: The University of Calgary, 1995
(  0) 0) |
| [4] |
Xu P L, Shu Y M, Niu X J, et al. High-Rate Multi-GNSS Attitude Determination: Experiments, Comparisons with Inertial Measurement Units and Applications of GNSS Rotational Seismology to the 2011 Tohoku MW9.0 Earthquake[J]. Measurement Science and Technology, 2019, 30(2) DOI:10.1088/1361-6501/aaf987
(  0) 0) |
| [5] |
甘雨, 隋立芬, 戚国宾, 等. 陆地导航中GNSS/陀螺仪组合实时测姿方法[J]. 武汉大学学报: 信息科学版, 2015, 40(3): 379-383 (Gan Yu, Sui Lifen, Qi Guobin, et al. A Real-Time Attitude Determination Approach for Land Navigation Based on GPS/Gyroscope Integration[J]. Geomatics and Information Science of Wuhan University, 2015, 40(3): 379-383)
(  0) 0) |
| [6] |
Lai Y C, Jan S S. Attitude Estimation Based on Fusion of Gyroscopes and Single Antenna GPS for Small UAVs under the Influence of Vibration[J]. GPS Solutions, 2011, 15(1): 67-77 DOI:10.1007/s10291-010-0171-y
(  0) 0) |
| [7] |
No H, Cho A, Kee C. Attitude Estimation Method for Small UAV under Accelerative Environment[J]. GPS Solutions, 2015, 19(3): 343-355 DOI:10.1007/s10291-014-0391-7
(  0) 0) |
| [8] |
蔡小波, 许厚泽, 王勇, 等. 车载三天线GNSS的直接法定姿及精度评估[J]. 武汉大学学报: 信息科学版, 2018, 43(6): 820-825 (Cai Xiaobo, Xu Houze, Wang Yong, et al. Direct Attitude Determination Method Based on Vehicle-Mounted Three-Antenna GNSS and the Accuracy Evaluation[J]. Geomatics and Information Science of Wuhan University, 2018, 43(6): 820-825)
(  0) 0) |
| [9] |
Chen W, Yu C, Cai M M, et al. Single-Antenna Attitude Determination Using GNSS for Low-Dynamic Carrier[C] China Satellite Navigation Conference, Shanghai, 2017
(  0) 0) |
| [10] |
王郁茗, 邵利民. 接收机天线姿态对多路径效应的影响研究[J]. 大地测量与地球动力学, 2019, 39(3): 273-278 (Wang Yuming, Shao Limin. Influence of Receiver Antenna Attitude on Multipath Effect[J]. Journal of Geodesy and Geodynamics, 2019, 39(3): 273-278)
(  0) 0) |
| [11] |
李乐乐, 贺凯飞, 王振杰, 等. GPS实时单站测速和相对测速的误差比较与精度分析[J]. 大地测量与地球动力学, 2019, 39(10): 1 063-1 069 (Li Lele, He Kaifei, Wang Zhenjie, et al. Error Comparison and Accuracy Analysis between Stand-Alone and Relative Velocity Determination Using GPS[J]. Journal of Geodesy and Geodynamics, 2019, 39(10): 1 063-1 069)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


