当大规模卫星观测值出现周跳时，实时PPP常出现重收敛现象。在观测条件较优时，某个历元通常仅有少数卫星发生周跳，通过分析卫星载波相位的验后残差进行实时周跳探测(detection)、定位(identification)和重置模糊度或周跳修复(adaptation)(即DIA算法)^[1]能准确探测周跳位置，在下个历元重置模糊度参数，且这种重置不会对定位结果产生很大影响，实时定位结果仍能保持很好的定位精度和稳定性。但在真实实时动态PPP情景下，由于受数据通信不稳定、观测环境差等因素的影响，尤其是当观测数据流短时中断再恢复时，实时观测数据可能会频繁出现周跳^[2-3]，DIA算法会错误探测周跳位置，进而错误重置模糊度参数。大量错误周跳信息会被保存在信息矩阵中，从而使定位结果重收敛，严重时会使滤波发散，产生不可预估的定位偏差，严重影响实时PPP结果的精度和可用性，对地震监测工作造成不利影响。

针对这些问题，本文首先采用所有卫星重新初始化模糊度参数的方法进行改进，并在此基础上引入附加电离层约束和附加坐标约束2种改进方法，利用NOTA(network of the America)测站网的实时观测数据流对3种改进方法进行实验验证，从定位精度、结果可用率等方面总结分析各方法的优缺点，为地震监测环境下的实时动态PPP处理提供参考。

1 方法 1.1 触发条件

在介绍快速重收敛方法之前，首先需设置合理的触发条件，以判断当前历元是否发生重收敛。对大量重收敛的时间序列进行汇总分析，本文经验性地提出以下触发条件：

1) 在实时PPP中，一般需要约10 min完成第1次收敛^[4]，因此当前处理历元应当是第600个历元之后。

2) 当前处理历元之前发生短时数据中断(20 min以内)，且中断前定位结果已收敛，在该情况下周跳探测还可检测出≥2个卫星相位观测值存有问题，则可认为会发生重收敛。

3) 当前处理历元未发生短时数据中断，但探测出大规模的卫星观测值发生周跳。一般来说，卫星数>6颗时，如果超过1/3的卫星载波相位存有问题，卫星数≤6颗时超过4个卫星相位存有问题，则可认为会发生重收敛。

1.2 重新初始化方法

当大规模卫星观测值发生周跳时，按原始周跳处理策略探测出周跳的卫星将在下个历元重置模糊度参数，这种大规模的重置模糊度相当于使PPP重新进入初始化过程，同时还存在错误重置的风险。另外，当实时观测数据流短时中断时，卫星硬件延迟的变化可忽略不计，卫星的模糊度参数在数据中断前后的变化可认为是整数，当数据流再次恢复时可看作所有卫星均发生周跳^[5]。

因此，本文首先采用重新初始化方法解决大规模周跳时的重收敛问题，根据触发条件判断某个历元是否发生重收敛，如果满足触发条件，则所有卫星均重置模糊度参数重新进行估计，滤波器的其他设置均保持不变。

1.3 附加电离层约束方法

非差非组合模型将L₁频率上的倾斜电离层延迟当作独立参数进行逐历元估计^[6-7]，本文采用随机游走模型估计L₁频率上的倾斜电离层延迟，可表示为：

$ \bar I_{{\rm{r}}, 1}^{\rm{s}}(k) = \hat I_{{\rm{r}}, 1}^{\rm{s}}(k - 1) + {\omega _{\bar I_{{\rm{r}}, 1}^{\rm{s}}}}, {\omega _{\bar I_{{\rm{r}}, 1}^{\rm{s}}}} \sim N\left( {0, \sigma _{{\omega _{\bar I_{{\rm{r}}, 1}^{\rm{s}}}}}^2} \right) $

(1)

$ \sigma _{{\omega _{\bar I_{{\rm{r}}, 1}^{\rm{s}}}}}^2 = q_{\bar I_{{\rm{r}}, 1}^{\rm{s}}}^2\left( {{t_k} - {t_{k - 1}}} \right) $

(2)

式中，$ \bar I_{{\rm{r}}, 1}^{\rm{s}}(k) $为第k历元的电离层延迟预测值；$ \hat I_{{\rm{r}}, 1}^{\rm{s}}(k - 1) $为第k－1历元的电离层延迟估计值；$ {\omega _{\bar I_{{\rm{r}}, 1}^{\rm{s}}}} $表示均值为0、方差为$ {\sigma _{{\omega _{\bar I_{{\rm{r}}, 1}^{\rm{s}}}}}^2} $的随机变量；方差${\sigma _{{\omega _{\bar I_{{\rm{r}}, 1}^{\rm{s}}}}}^2} $为电离层延迟随机游走过程的过程噪声$q_{\bar I_{{\rm{r}}, 1}^{\rm{s}}}^2 $与前后历元时间差(t_k－t_k－1) 的乘积。

正常情况下，本文将过程噪声$ q_{\bar I_{{\rm{r}}, 1}^{\rm{s}}}^2 $设置为4 m/$ \sqrt {\rm{s}} $，而在重新初始化时，由于电离层延迟在短期内存在强烈的时间相关性，在时间更新中可将过程噪声缩小至一定水平，如原来的1/100，相当于在重收敛开始时“隐式”预报电离层延迟参数。另外，采用当前历元前1个时间窗口(本文取120 s)内的电离层延迟估计值进行线性拟合也可对电离层参数进行“显式”预报。本文对这2种预报方法进行对比实验发现，其效果几乎处于同一水平，考虑到存储和计算负担，本文采用“隐式”预报策略。电离层延迟在短时间内变化平缓，因此在重新初始化后一段时间内(60 s)对电离层延迟参数施加强约束以保证其在该时段内缓慢变化。同时，在滤波器中对电离层延迟和模糊度参数进行估计，较精确的电离层延迟参数可在重收敛过程中加快模糊度收敛^[8]。

1.4 附加坐标约束方法

本文采用随机游走模型估计测站坐标，将测站坐标的过程噪声$ q_{{{\bar X}_{\rm{r}}}}^2 $设置为1 m/$ \sqrt {\rm{s}} $。

由于地震监测工作通常是在已知精确坐标的静态测站上进行实时PPP处理，测站的位置信息也可作为约束信息来解决重收敛问题。当某个历元触发重新初始化后，如之前的定位结果已经收敛，说明此时的测站坐标参数已被准确估计，可在重新初始化后一段时间内对测站坐标参数施加强约束，加速模糊度参数的收敛；如未收敛，则需要在重新初始化的第1个历元将测站坐标先验值固定为已知精确坐标，再对其施加强约束。

附加坐标约束方法可极大提高定位结果的精度水平和收敛性能，但必要条件是测站在使用该方法期间未发生位移且精准坐标已知，如测站因地震等发生真实位移，该方法将长期损害定位结果。本文在附加坐标约束后会持续监测，如定位结果在20 min内无法收敛，则认为此时的附加坐标约束错误，立即初始化滤波器，并重新开始PPP处理。

2 实验与结果分析 2.1 实验设置与处理策略

为验证和分析本文快速重收敛方法的效果，选取NOTA测站网中9个经常发生重收敛的测站，对2019年doy324及2020年doy251~318的实时观测数据流进行伪实时处理。图 1为9个测站的分布情况，测站大多分布于中纬度地区，区域电离层较稳定^[9]，可满足附加电离层约束方法的假设条件，仅AC44站位于61°N。实验具体设置和处理策略见表 1。

本文使用Kalman滤波器对数据进行处理，利用§1.1中触发条件进行判断，采用4种方法对实验数据进行处理：1)不采用任何措施，保持原始的部分模糊度重置策略；2)重新初始化，所有卫星重置模糊度参数；3)附加电离层约束，在重新初始化开始历元的时间更新中，将电离层延迟参数的过程噪声$ q_{\bar I_{{\rm{r}}, 1}^{\rm{s}}}^2 $缩小至4 cm/$ \sqrt {\rm{s}} $，“隐式”预报电离层延迟参数，并在之后的60 s内对滤波器中的电离层延迟参数施加强约束；4)附加坐标约束，在重新初始化后，如之前的滤波结果已经收敛，则直接在初始化开始后2 s内对测站坐标参数施加强约束；否则，先将测站坐标先验值固定为已知的精确坐标，再对其施加2 s强约束。

2.2 实验结果与分析 2.2.1 单站处理结果与分析

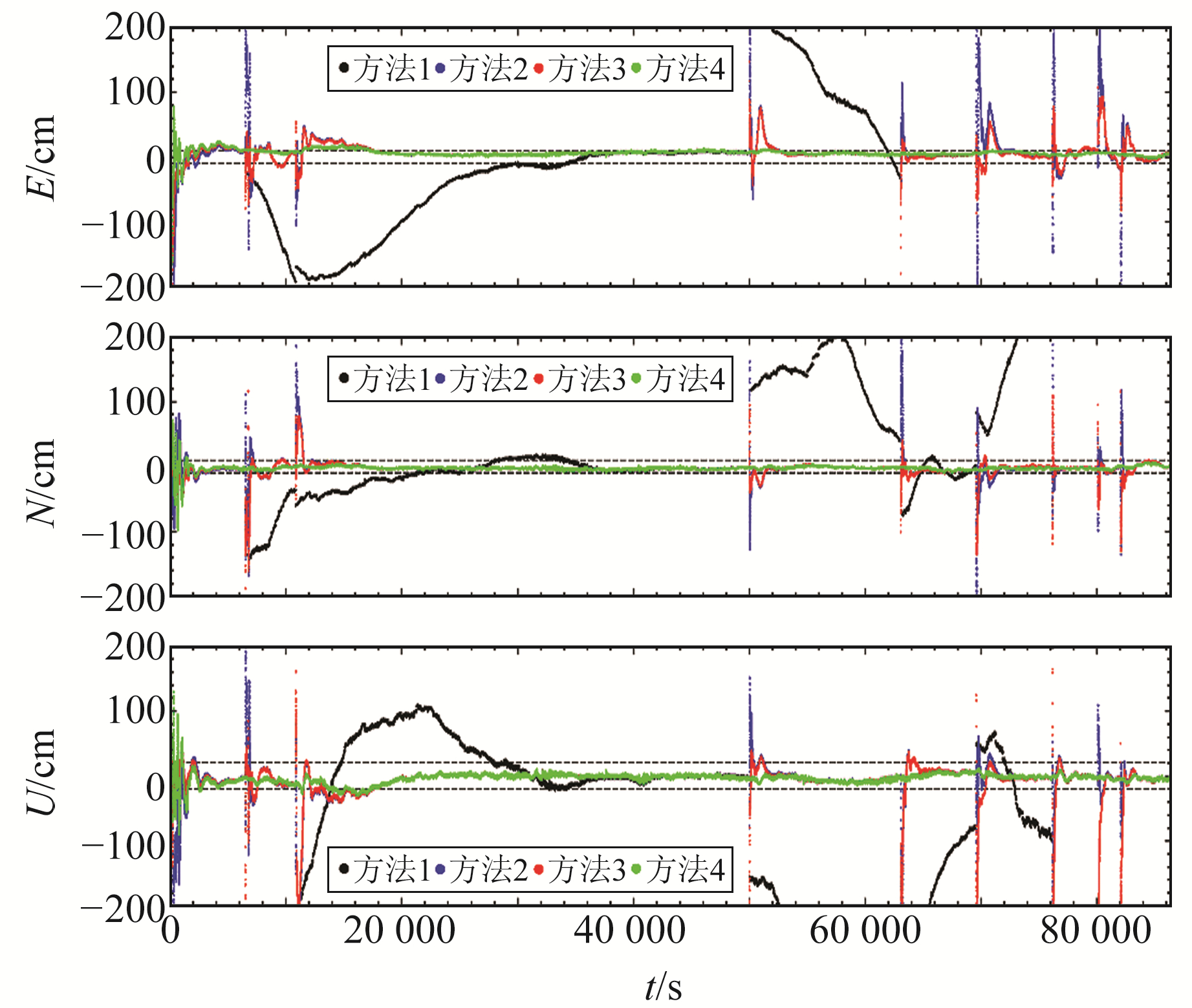
本文将NGL(Nevada Geodetic Laboratory, http://geodesy.unr.edu/)^[10]提供的每天PPP静态解作为测站参考坐标计算定位偏差。图 2为ANA1站2019年doy324的定位结果时间序列，从图中可以看出，当大规模周跳存在且不采取任何措施时，定位结果会产生很大跳变，49 986 s之后定位结果处于发散状态。另外3种方法均能解决发散问题，获得连续的定位结果，但重新初始化和附加电离层约束方法在采取措施后一段时间内仍保持重收敛过程。重新初始化方法在重收敛时段内时间序列的波动最大能达到水平方向3 m、垂直方向4 m，附加电离层约束方法能在一定程度上减小波动幅度，在E方向上表现明显；附加坐标约束方法效果最好，可直接消除重收敛问题，使定位结果在第1次初始化后始终够保持高定位精度。

表 2(单位cm)为4种方法的定位结果在第1次初始化后E、N、U方向和三维位置的均方根误差(RMS)。由表 2可知，不采取任何措施的定位精度很差，无法满足地震监测的精度要求；采用重新初始化方法能够显著提高定位精度，有利于从位移序列中更好地监测地震波信号；附加电离层约束方法可进一步提高定位精度，相比于重新初始化方法，定位精度在E、N、U方向和三维位置上分别提高42%、21%、18%、27%；附加坐标约束方法的定位精度最高，相比于重新初始化方法，其定位精度在E、N、U方向和三维位置上分别提高65%、62%、70%、67%。

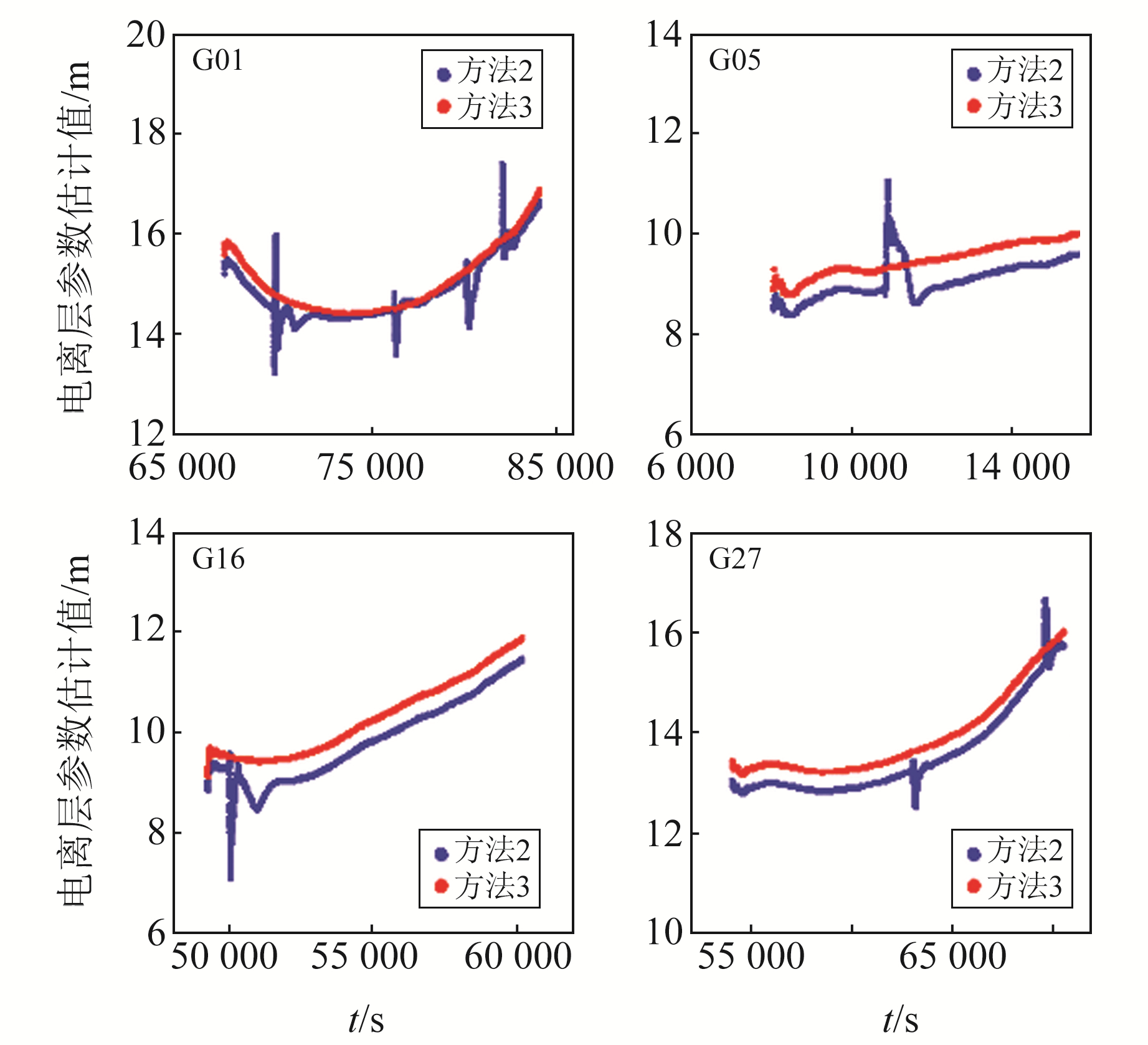
图 3为G01、G05、G16、G27卫星L₁频率的一阶电离层延迟估计值序列，从图中可以看出，仅采用重新初始化方法时，电离层估计值在相应的重收敛历元处会产生1~3 m的波动，这显然不符合电离层参数正常的变化情况；采用附加电离层约束方法后，电离层估计值序列变得平滑，在相应的重收敛历元处未出现跳变，而是缓慢变化，这更符合真实情况。

实时PPP结果的可用性也十分重要。本文将滤波收敛定义为某个历元及某后连续20个历元E、N、U方向的定位偏差均优于10 cm、10 cm、20 cm，否则继续向后重复判断收敛方法；同时将定位结果可用率定义为时间序列中处于收敛时期的历元数占总输出历元数的比例，定位结果可用率可反映PPP处理时段内定位结果的可用性，是评估实时处理性能的重要指标。不采取任何措施时，定位结果可用率仅为0.2，说明实时PPP处理效果非常差，无法以高置信水平监测地震信号；采用重新初始化方法后，可用率上升至0.69，可提高PPP处理性能；附加电离层约束后，定位结果可用率也为0.69，这主要是因为本文未进行模糊度固定，在重收敛阶段无法大幅加速模糊度收敛。重新初始化方法的平均重收敛时间为24.9 min，附加电离层约束后平均重收敛时间为23.7 min，只缩短了1.2 min，因此只能在重收敛阶段减小定位结果的波动范围，无法加快重收敛速度及提升定位精度，故结果可用率未发生变化。附加坐标约束方法依然表现最好，不仅可提高定位精度，还可在重收敛阶段直接使模糊度参数收敛，消除重收敛问题，定位结果可用率上升至0.82。

2.2.2 多站处理结果与分析

图 4为所有测站2020年doy251~318每天的三维位置RMS值分布情况，设置阈值为50 cm，当三维位置RMS值超过50 cm时，认为重收敛问题对定位结果造成严重影响，位移信息不可用。由图 4可知，不采取任何措施时，三维位置RMS值大于50 cm的定位结果占51.59%，处理效果很差；采用重新初始化方法后，RMS值大于50 cm的比例降至11.90%，且集中分布在20 cm以内，定位结果精度较高；采用附加电离层约束方法后，RMS值在20 cm范围内的占比有所提升，但大于50 cm的比例反而升高至16.27%，这主要是由于实时环境下各测站情况复杂且不同，而本文采用统一的附加电离层约束策略，部分数据质量差的测站降低了整体结果的精度。附加坐标约束方法不受测站影响，可持续获得高精度的定位结果，86%的RMS值在20 cm以内，且RMS值大于50 cm的定位结果仅占2.78%。

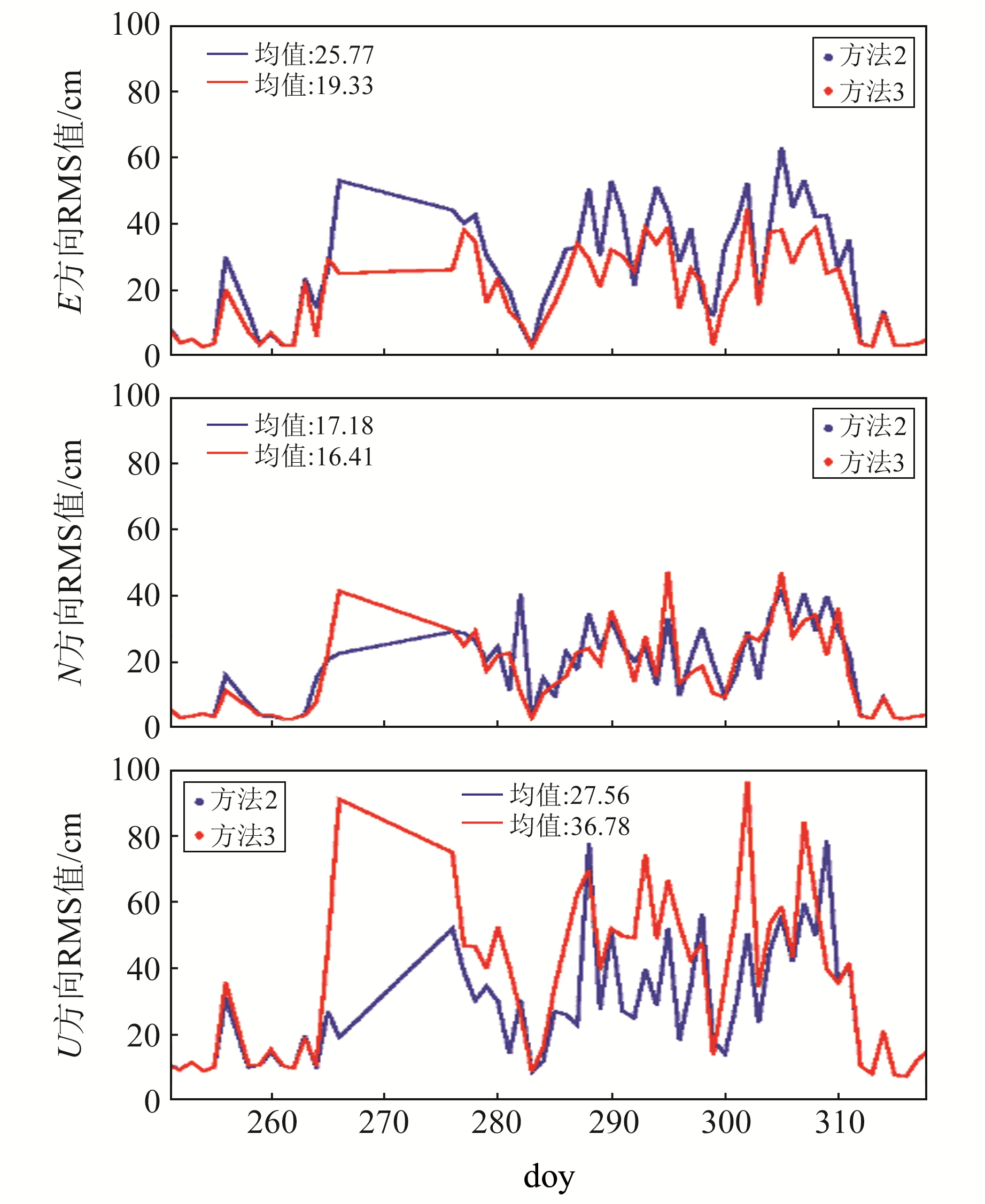
图 4中附加电离层约束方法的RMS值大于50 cm所占的比例比重新初始化方法大，主要受部分重收敛问题特别严重的测站影响所致。以P313站和LGWD站(LGWD在doy280之前无数据)E、N、U方向的RMS值为例(图 5和6)，其中P313站在整个时段内及LGWD站在doy299采用重新初始化方法后，定位结果RMS值仍保持在高水平，P313站在U方向的RMS值基本大于30 cm，表明重新初始化不足以抵消大量周跳造成的不利影响，同时数据质量较差时附加电离层约束反而会降低定位结果的质量；而LGWD站除doy299外，其RMS值基本在30 cm以内，采用附加电离层约束后RMS值进一步减小，定位精度有所提高。由此可知，采用附加电离层约束方法不能一概而论，其处理效果受不同测站不同数据的影响，因此不同测站应采用不同的电离层约束策略来获得最好的处理效果。

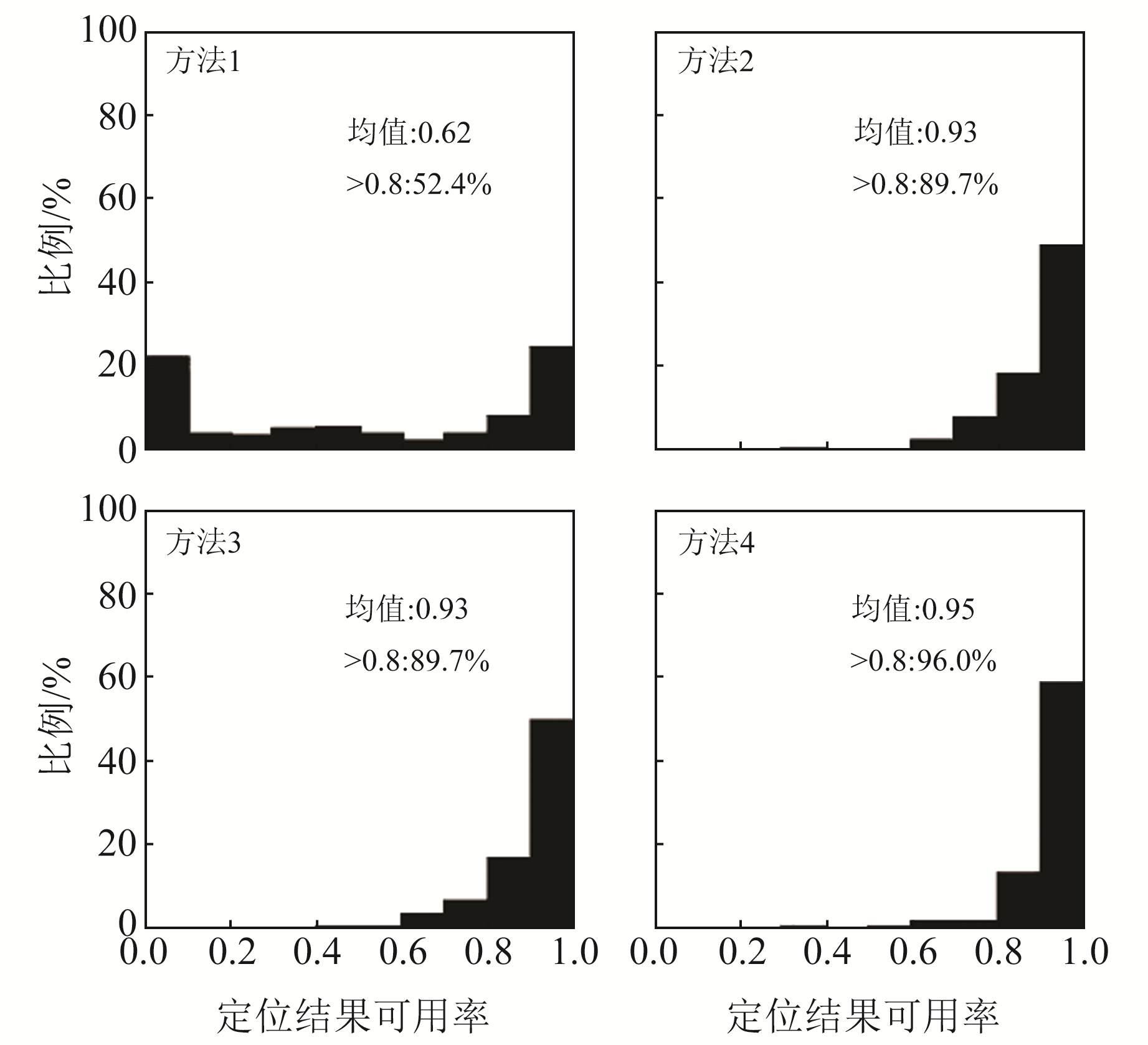
图 7为2020年doy251~318所有测站每天的定位结果可用率分布情况，可以看出，不采取任何措施时的定位结果可用率最差，平均值仅为0.62，可用率大于0.8的比例仅为52.4%；采用重新初始化方法后，定位结果可用率大幅提升，平均值上升至0.93，大于0.8的比例增至89.7%；附加电离层约束后，定位结果可用率相比重新初始化方法无变化，表明在未进行模糊度固定的情况下附加电离层约束加快重收敛速度的作用较小，这与ANA1站得到的结论一致；附加坐标约束方法可进一步提高定位结果可用率，平均值为0.95，大于0.8的比例增至96.0%，基本可保证每天的定位结果可用率在0.8以上，可极大提高实时PPP结果的可用性。

3 结语

本文利用NOTA测站网的实时观测数据流，通过伪实时处理对3种改进重收敛问题的方法进行实验验证。在单站处理中，不采取任何措施、重新初始化、附加电离层约束和附加坐标约束方法的定位结果三维位置RMS值分别为420.68 cm、44.54 cm、32.53 cm、14.65 cm，定位结果可用率分别为0.20、0.69、0.69、0.82；在多测站67 d的处理中，4种方法定位结果三维位置RMS值大于50 cm所占的比例分别为51.59%、11.90%、16.27%、2.78%，定位结果可用率平均值分别为0.62、0.93、0.93、0.95，大于0.8所占的比例分别为52.4%、89.7%、89.7%、96.0%。

分析实验结果可知，重新初始化方法能有效解决发生大规模周跳时定位结果发散的问题，定位精度和结果可用率均有明显提升，但相应处理时段内仍会出现重收敛现象；附加电离层约束方法易受测站和数据的影响，处理方式不能一概而论，对于数据质量较好的测站能够提高定位精度，但对于问题严重的测站反而会降低定位结果的精度，在使用时需充分考虑测站情况或进行模糊度固定才能获得最好的效果；附加坐标约束方法的改进效果最好，且不受其他因素影响，可直接消除重收敛过程，使定位结果保持高精度和高可用率，但该方法在测站坐标信息有误差或发生位移时会得到不可逆的错误结果，必须采取相应的措施来改正。

重新初始化、附加电离层约束、附加坐标约束3种方法在定位精度、重收敛时间、定位结果可用率、适用性等方面各有优劣，在地震监测工作中可根据具体情况采取合适的策略来获得高精度的实时动态PPP处理结果，以更好地捕捉地震信号，提高地震监测能力。