2. 中国科学院大学,北京市玉泉路19号甲,100049;
3. 华中科技大学物理学院,武汉市珞喻路1037号,430074
由于卫星在空间受多种因素的影响,在重力场反演过程中需对加速度计观测的非保守力进行校正[1-4]。不同机构针对加速度计校正采用的方法不同。加速度计的校正主要是通过建立加速度计校正参数的设计矩阵与轨道或星间距变率的观测方程来实现的,影响因素较多,是一个十分复杂的过程[5-10],而时变重力场的解算精度和加速度校正策略具有一定的关联。
相较于GRACE卫星,GRACE-FO卫星搭载了激光测距设备,对卫星的姿态有较高的要求,会通过多次点火来调整卫星姿态以维持激光测距,而加速度计能够敏感捕捉到卫星平台频繁机动引起的信号,并体现在加速度计观测数据中。因此,在GRACE-FO时变重力场反演中,需要探索加速度计校正策略对时变重力场解算的影响,并综合分析满足重力场反演需要的加速度计校正方式。本文以GRACE-FO卫星2019-01数据为例,探索不同加速度计偏差参数校正策略对时变重力场反演结果的影响。
1 加速度计校正基本理论加速度计校正是通过建立加速度计参数设计矩阵与轨道观测方程,并对观测方程进行最小二乘求解,以实现对加速度计参数的校正。本文通过采用动力学方法建立观测方程进行加速度计校正。
1.1 动力学基本方法卫星在空间飞行满足牛顿运动学定律,可写成如下形式:
| $ \mathit{\boldsymbol{\ddot r}}\left( t \right) = \mathit{\boldsymbol{a}}(t;{\mathit{\boldsymbol{r}}_0}, {\mathit{\boldsymbol{\dot r}}_0}, \mathit{\boldsymbol{r}}, \mathit{\boldsymbol{\dot r}}, {\rm{ }}\mathit{\boldsymbol{y}}) $ | (1) |
式中,
| $ \Delta \mathit{\boldsymbol{r}} = \mathit{\boldsymbol{r}}\left( t \right) - {\mathit{\boldsymbol{r}}_0}\left( t \right) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_r}\delta ({\mathit{\boldsymbol{r}}_0}, {{\mathit{\boldsymbol{\dot r}}}_0}) + {\mathit{\boldsymbol{S}}_r}\delta \mathit{\boldsymbol{P}} $ | (2) |
式中,Φr、Sr为状态转移矩阵和参数敏感矩阵,是通过对r(t) 在r0(t)处进行泰勒展开,取线性形式得到的,即
| $ \mathit{\boldsymbol{r}}\left( t \right) = {\mathit{\boldsymbol{r}}_0}\left( t \right) + \frac{{\partial {\mathit{\boldsymbol{r}}_0}\left( t \right)}}{{\partial \mathit{\boldsymbol{y}}}}\Delta \mathit{\boldsymbol{y}} $ | (3) |
同理可得,星间距变率的观测方程为:
| $ \mathit{\boldsymbol{\dot \rho }}\left( t \right) = {{\mathit{\boldsymbol{\dot \rho }}}_0}\left( t \right) + \frac{{\partial {{\mathit{\boldsymbol{\dot \rho }}}_0}\left( t \right)}}{{\partial {r_{12}}}}\frac{{\partial {r_{12}}}}{{\partial \mathit{\boldsymbol{x}}}}\Delta \mathit{\boldsymbol{x}} $ | (4) |
此外,在重力场反演过程中需要联合轨道和星间距变率观测方程进行求解,其法方程可写成如下形式:
| $ \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{N}}_{{\rm{leo}}}}\mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{b}}_{{\rm{leo}}}}}\\ {{\mathit{\boldsymbol{N}}_{{\rm{kbrr}}}}\mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{b}}_{{\rm{kbrr}}}}} \end{array}} \right) $ | (5) |
式中,Nleo、Nkbrr为轨道和星间距变率观测的法方程,bleo、bkbrr为观测值,y为待求量。
1.2 加速度计偏差参数校正策略加速度计的校正是在卫星科学坐标系下进行的,其形式可写成[11]:
| $ {\rm{AC}}{{\rm{C}}_{{\rm{new}}}} = B + S\cdot{\rm{ACC1B}} $ | (6) |
式中,ACCnew为校正后的加速度计数据,B为加速度计偏差因子,S为尺度因子,ACC1B为L1B加速度计数据。由于本文只考虑加速度计的偏差校正,因此将加速度计的尺度参数设置为单位阵。对于加速度计的偏差因子B,设置的校正形式为:
| $ B = {C_0} + {C_1} \times t $ | (7) |
式中,C0、C1为待求常数;t为时间,从每个弧段起始算起。设置加速度计校正的弧长为24 h,表 1为偏差参数校正策略,包括常数偏差参数形式(估计C0项)和线性偏差参数形式(估计C0、C1项),X、Y、Z表示的是SFR坐标系。
|
|
表 1 加速度计偏差参数校正策略 Tab. 1 Accelerometer estimation parameter strategies |
本文采用JPL发布的GNV1B轨道数据对GRACE-FO两颗卫星的加速度计偏差参数进行校正,在校正过程中需同时估计卫星的初始状态,所用数据主要为ACT1B、SCA1B、KBR1B、GNV1B,在构建参考轨道时采用的力模型见表 2。
|
|
表 2 力模型 Tab. 2 Force models |
本文通过分析表 1中的33种偏差参数校正策略,对比轨道拟合结果及60阶无约束重力场结果来探讨所选取的加速度计校正策略对时变重力场解算的影响。
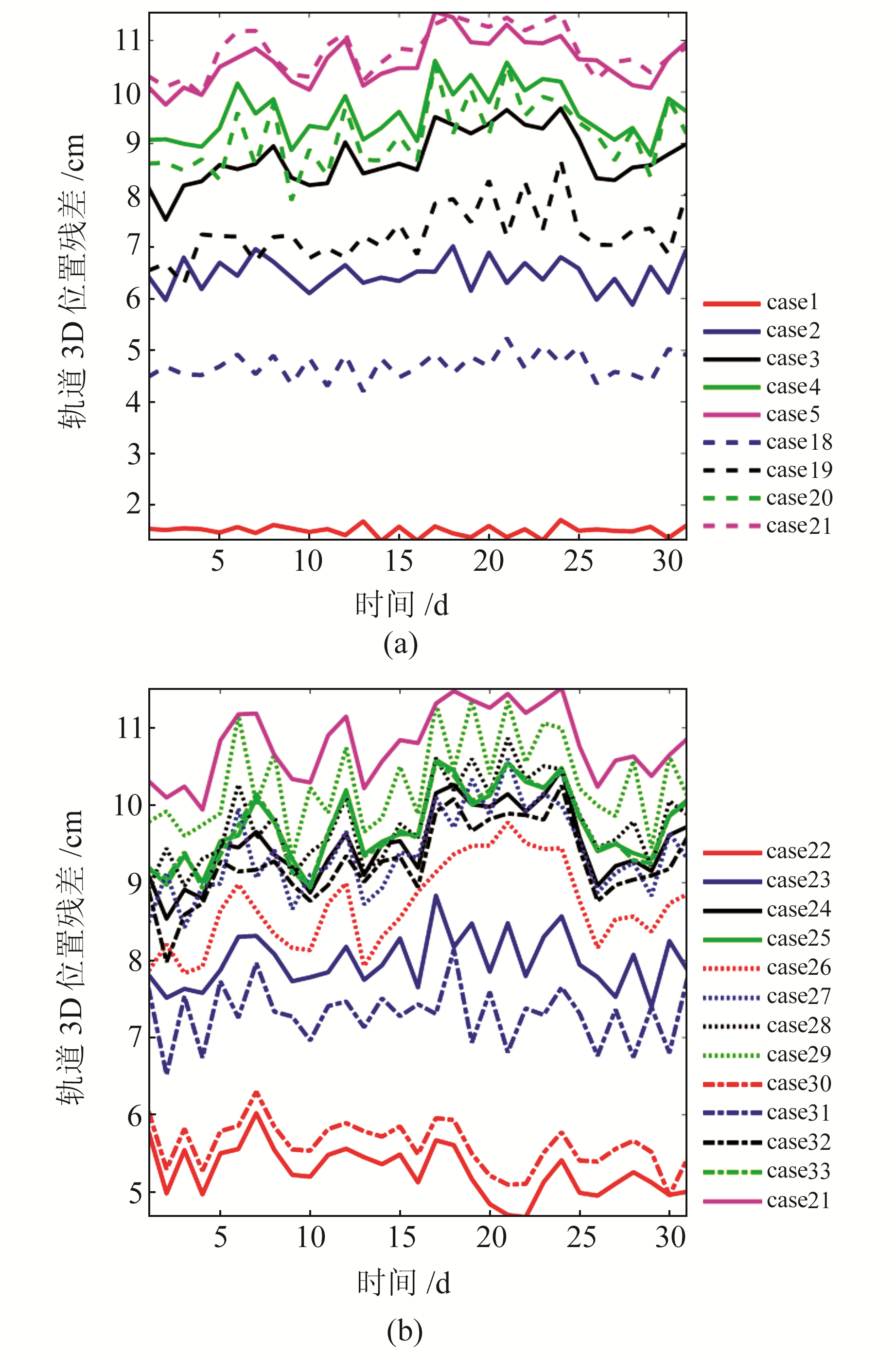
2.1 轨道拟合结果表 3为计算的每日轨道三轴残差(RMS)结果和轨道3D残差结果。结合表 1和3,由case1~5(估计C0项)和case18~21(估计C0、C1项)可以看出,当只估计偏差参数常数项C0时,X、Y、Z方向校正的加速度计参数由72个减小到3个,计算的轨道三轴残差逐渐增大,而轨道3D残差也从1.51 cm逐渐增大到10 cm左右;同时估计加速度计常数项C0和线性项C1时,X、Y、Z方向校正的加速度计参数由48个减少到6个,轨道3D残差由5 cm左右逐渐增大到10.97 cm。图 1(a)为计算的轨道3D残差,图中实线为采用常数偏差参数形式(估计C0项),虚线为采用线性偏差参数形式(估计C0、C1项),可以看出,计算的轨道3D残差随校正频率的减小而逐渐增大;对比2种形式的计算结果发现,在校正频率相同的情况下,加速度计校正参数越多轨道残差越小,拟合的轨道越优,24 h弧段每24 h校正1次加速度计参数时2种估计形式获得的残差没有表现出明显差异。
|
|
表 3 采用不同策略拟合的轨道残差 Tab. 3 Orbit residuals fitted with different strategies |
|
图 1 不同策略拟合的轨道3D位置残差 Fig. 1 Orbit 3D position residuals fitted by different strategies |
加速度计Y轴为非敏感轴,其测量精度相比于X轴和Z轴约低1个量级。进一步考察对加速度计三轴分别采用不同校正频率进行计算获取的轨道拟合结果,分析X、Y和Z轴采用每1 h、3 h、6 h、12 h、24 h校正1次计算所拟合的轨道残差。结合表 1和3中case5~17估计C0项和case21~33估计C0、C1项的结果可以看出:1)仅针对X轴,只估计C0项(case5~9)时,所校正的参数由1 h的26个减少到24 h的3个,计算的轨道3D残差由6.75 cm增大到10.60 cm;当同时估计C0和C1项(case21~25)时,校正参数由1 h的52个减少到24 h的6个,计算的轨道3D残差由5.27 cm增大到10.79 cm;2)仅针对Y轴,只估计C0项(case10~13)时,所校正的参数由1 h的26个减少到24 h的3个,计算的轨道3D残差由8.71 cm增大到10.60 cm;当同时估C0和C1项(case26~29)时,校正参数由1 h的52个减少到24 h的6个,轨道3D残差由8.70 cm增大到10.79 cm,并且对比发现,仅对Y轴进行不同校正频率分析计算的残差整体偏大;3)仅针对Z轴,只估计C0项(case14~17)时,所校正的参数由1 h的26个减少到24 h的3个,计算的轨道3D残差由6.35 cm增大到10.60 cm;当同时估计C0和C1项(case30~33)时,校正参数由1 h的52个减少到24 h的6个,计算的轨道3D残差由5.61 cm增大到10.79 cm。
另外,当校正的参数个数相同时(如case22、case26、case30),所计算的轨道3D残差在X轴和Z轴上基本相同(5.27 cm、5.61 cm),但在Y轴上差异较大(8.70 cm)。将case21~33所计算的轨道3D残差结果反映在图 1(b)中,由图中case22~25可知,在对X、Y、Z轴采用不同的校正频率时,加速度计的校正参数越多轨道残差越小,轨道拟合结果越优;校正参数个数相同时,拟合的轨道残差在X轴和Z轴上基本接近,约为5.5 cm,在Y轴上结果较差,约为8.7 cm。
2.2 时变重力场结果 2.2.1 三轴采用同样的校正形式图 2为对加速度计三轴采用相同的校正频率所得的重力场结果,其中实线为采用常数偏差参数形式(估计C0项)计算的以大地水准面高表示的重力场阶方差,虚线为采用线性偏差参数形式(估计C0、C1项)的计算结果,通常认为40阶之前由时变重力场信号主导,大于40阶误差逐渐占主导。由图可知,2~40阶采用的几种策略所计算的阶方差基本相同;40阶之后除了case1外,其他几种策略计算的阶方差结果差别不大;60阶几种策略的累计大地水准面阶方差均为2.34 cm左右。对加速度计三轴采用相同校正形式不同策略计算出的重力场结果基本相同,需要指出的是,case1计算出的60阶累计大地水准面阶方差在2.49 cm左右,其原因可能是case1采用的是1 h校正频率的偏差策略,所校正的加速度计参数过多或参数形式并不合适,出现过拟合现象,从而吸收了部分重力场信号,导致计算结果产生偏差。

|
图 2 不同策略反演的重力场 Fig. 2 The gravity field determination by different cases |
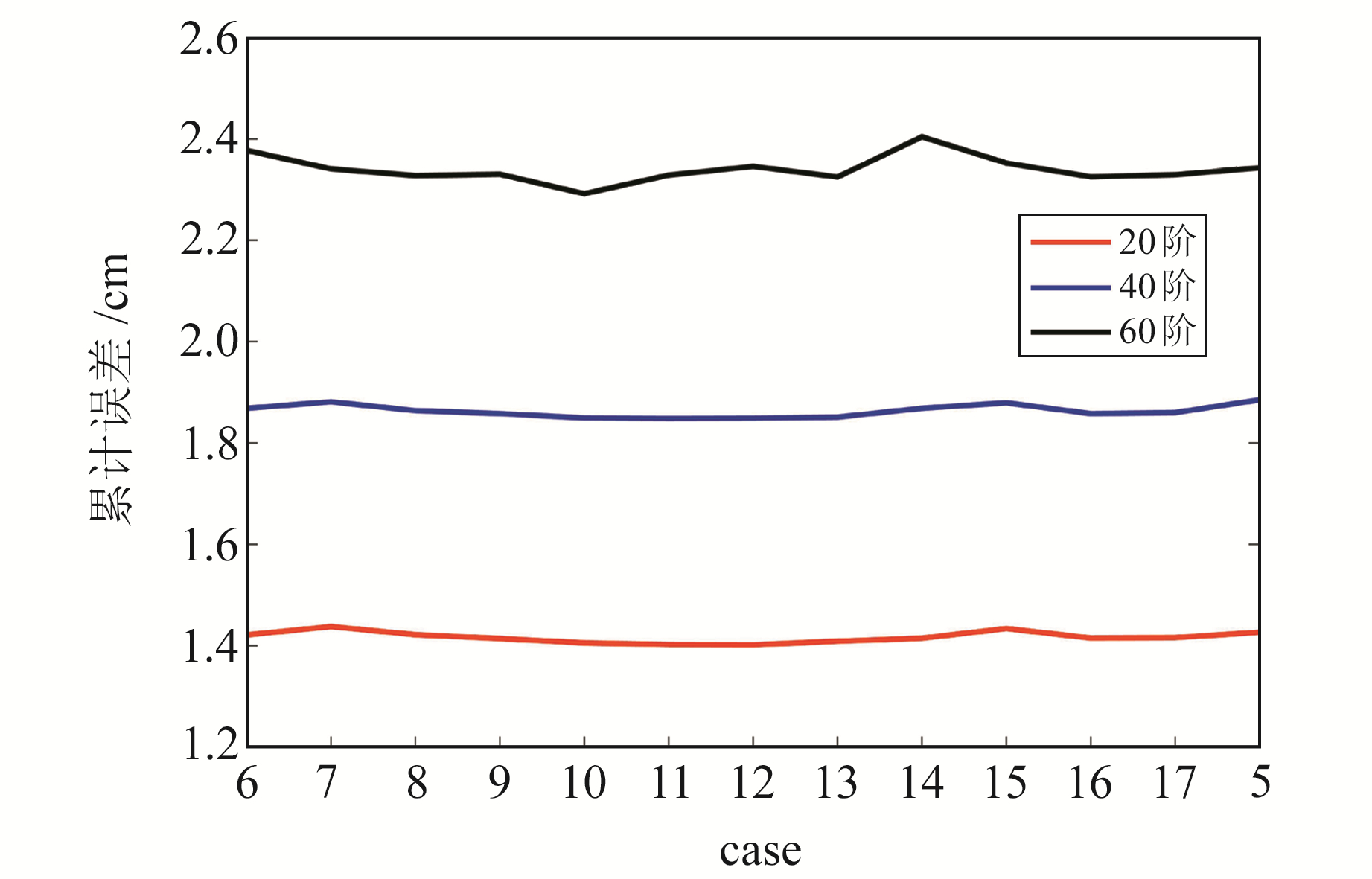
采用常数偏差参数形式(估计C0项)对加速度计X、Y、Z三轴分别采用不同校正参数个数计算的重力场大地水准面累计阶方差结果见表 4。由表可见,20阶和40阶的累计大地水准面阶方差基本相同,约为1.42 cm和1.86 cm,反映在图 3则是红线及蓝线比较平缓。表 4统计结果显示,60阶累计大地水准面阶方差并未随加速度计校正参数个数的减少变差,如case7~9、case11~13、case15~17等,加速度计校正参数由每天10个减少到4个,计算结果基本保持一致,且当三轴校正参数个数相同(参数个数为10)时,case7、case11、case15计算的60阶累计大地水准面阶方差基本相同,约为2.34 cm(参数个数为6和4时,其结果与参数个数为10的结果基本一致)。而仅当参数个数为26时,分别对应case6(X轴校正频率为1 h,Y轴、Z轴为24 h)、case10(Y轴校正频率为1 h,X轴、Z轴为24 h)和case14(Z轴校正频率为1 h,X轴、Y轴为24 h),计算结果差异明显,约为2.38 cm、2.29 cm和2.40 cm,其中case10结果明显优于case6和case14。上述分析表明,采用常数偏差参数形式进行加速度校正时,参数个数并不能直接影响时变重力场解算的结果,但当不同方向的校正频率不同时,其中Y轴1 h校正1次、X轴和Z轴24 h校正1次,解算结果明显优于表 4中其他策略。
|
|
表 4 20阶、40阶、60阶重力场累计阶方差(常数偏差参数形式) Tab. 4 Cumulative degree variance of the 20, 40, 60 gravity field(constant strategies) |
|
图 3 20、40、60阶重力场累计阶方差(常数偏差形式) Fig. 3 Cumulative degree variance of the 20, 40, 60 gravity field(constant strategies) |
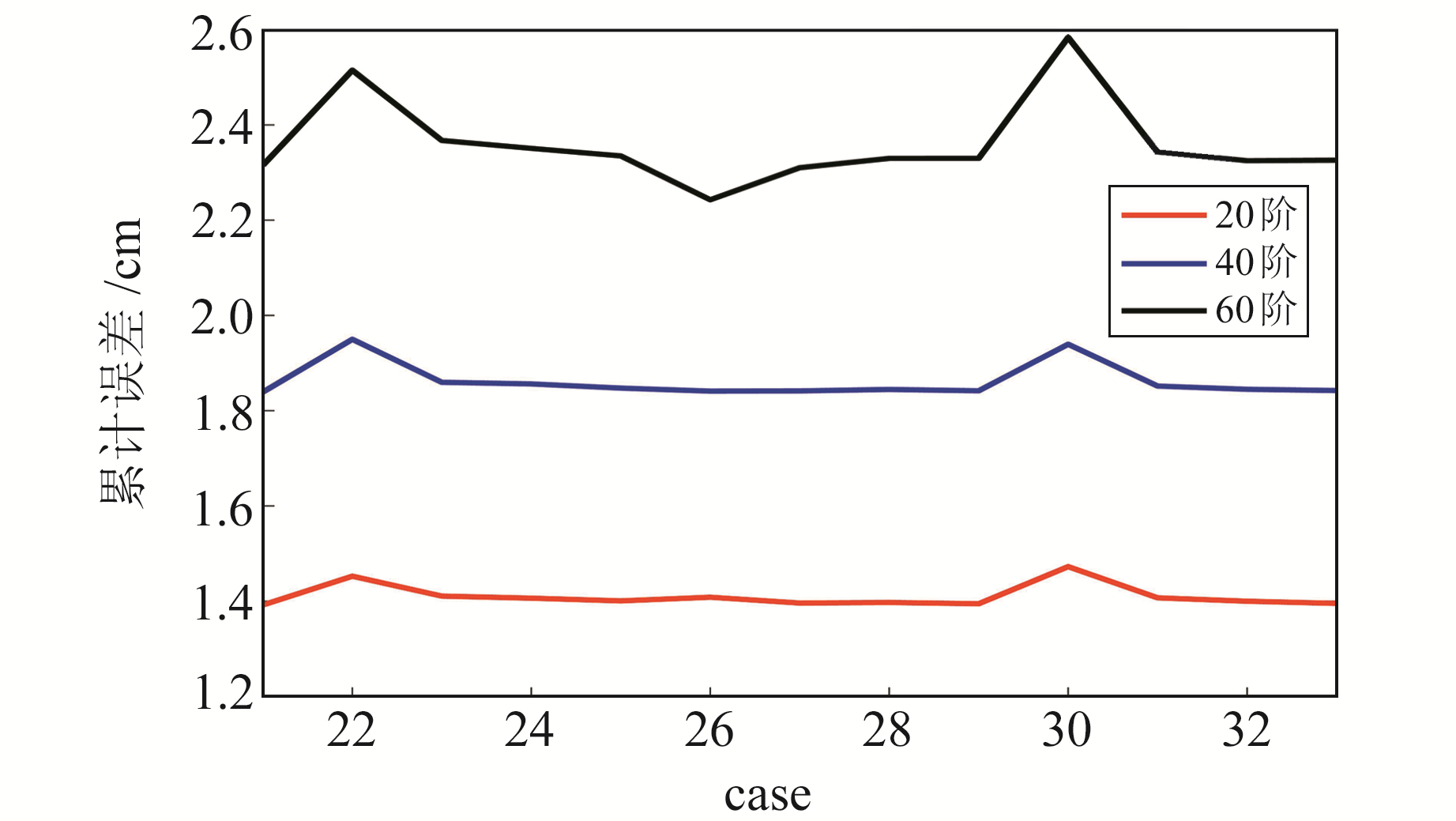
进一步分析线性偏差参数形式(估计C0、C1项)对时变重力场解算结果的影响。表 5为采用线性偏差参数形式(估计C0、C1项)对加速度计三轴分别采用不同校正频率统计的20阶、40阶和60阶累计大地水准面阶方差,其中case22~25为X轴分别采用1 h、3 h、6 h、12 h校正1次的加速度计线性偏差算例,Y轴、Z轴校正频率固定为24 h;case26~29和case30~33采用同样的处理方式,只分别改变Y轴和Z轴的校正频率,以便从校正参数个数和不同方向的校正形式进行分析。从表 5和图 4可以看出,校正参数个数为20、12、8时的计算结果基本相同,时变重力场解算结果未表现出明显差异;而当校正参数个数为52时,在20、40和60阶累计阶方差处case22、case30的误差较大,分别约为1.45 cm、1.47 cm,1.95 cm、1.94 cm和2.51 cm、2.58 cm,为所有策略中结果较差的2个。其中,case26在20、40、60阶的大地水准面累计阶方差为1.41 cm、1.84 cm、2.24 cm,为最优策略。不难看出,对于采用线性偏差参数形式进行加速度计校正时,参数个数的影响小于校正策略,如case22、case26和case30的结果表现出明显差异,case26为所有策略中最优,即在X轴、Z轴上采用1 h校正频率所计算的阶方差会明显变差,而对Y轴采用1 h校正频率计算的阶方差会明显提高,这与采用常数偏差参数形式进行加速度计校正所得结论基本一致。
|
|
表 5 20阶、40阶、60阶累计阶方差(线性偏差参数形式) Tab. 5 Cumulative degree variance of the 20, 40, 60 gravity field(linear strategies) |
|
图 4 20、40、60阶重力场累计阶方差(线性偏差参数形式) Fig. 4 Cumulative degree variance of the 20, 40, 60 gravity field(linear strategies) |
采用不同的加速度计校正策略,从计算的重力场阶方差结果可以看出:1)对加速度计X、Y、Z三轴选用相同的校正频率,采用常数偏差参数形式(估计C0项)所得结果与线性偏差参数形式(估计C0、C1项)基本相同,60阶累计误差均为2.34 cm左右;2)对加速度计X、Y、Z三轴分别采用不同的校正频率,X轴、Z轴采用1 h校正频率的结果最差,采用常数偏差参数形式和线性偏差参数形式计算的60阶累计阶方差分别约为2.38 cm、2.51 cm,2.40 cm、2.58 cm,对于Y轴采用1 h校正频率的结果最优,采用常数偏差参数形式和线性偏差参数形式计算的60阶累计误差约为2.29 cm、2.24 cm,其余结果均为2.34 cm左右。综合对比分析采用的不同校正策略发现,case26采用线性偏差参数形式(估计C0、C1项),X轴、Z轴24 h校正1次、Y轴1 h校正1次时结果最优。
图 5为计算的阶方差结果和各模型的空间分布,由图 5(a)可见,重力场阶方差与GFZ、JPL模型的结果较为接近,且从模型的空间分布可以看出,计算的时变重力场模型在信号强度、信号明显区域(如亚马逊流域、格陵兰岛、华北平原、中东地区及南极大陆等)都与官方结果一致。

|
图 5 阶方差与模型空间分布 Fig. 5 Degree variance and models spatial distribution |
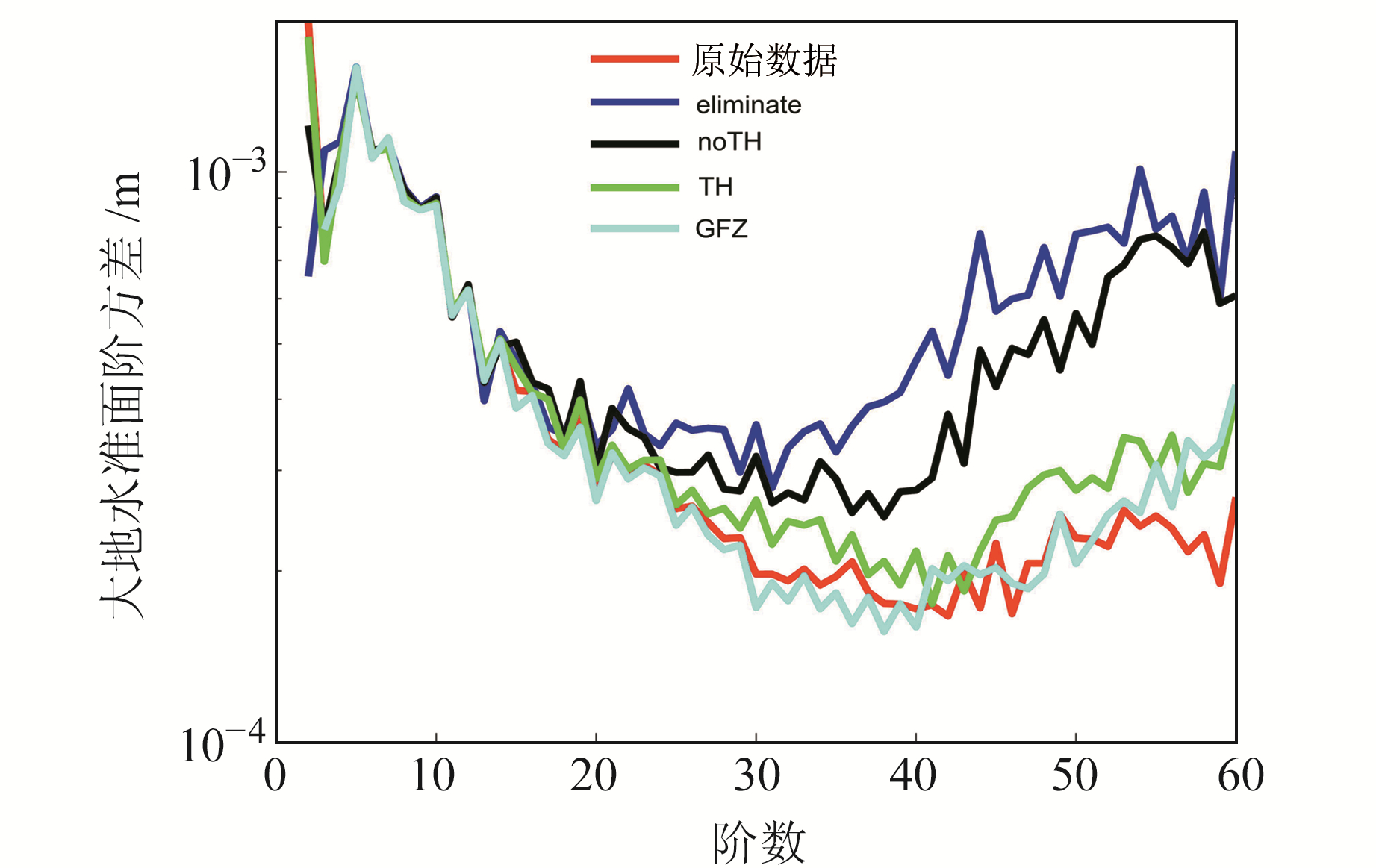
采用常数和线性偏差参数形式,利用不同策略进行加速度计校正后发现,加速度计校正参数个数的多少对重力场解算结果的影响并不明显,而当采用Y轴1 h校正1次、其他轴24 h校正1次的策略时,无论采用常数形式还是线性形式,结果均为最优。由于Y轴为不敏感轴,且GRACE-FO的数据采集对姿态要求较高,而卫星平台频繁机动,根据GRACE-FO推进器工作原理,其机动方向主要体现在Y轴和Z轴上,因此可通过处理加速度数据中推进器信号来解决此问题[12]。首先考虑在L1A-L1B数据中采用推进器模型(thruster)剔除影响加速度计数据的信号,并在L1B数据中采用剔除的推进器信号,然后对剔除部分进行插值来分析推进器因素对重力场反演结果的影响。图 6中红线、蓝线、黑线、绿线依次为直接采用原始数据、采用剔除插值方法(eliminate)、在L1A-L1B数据处理中未采用推进器模型(noTH)及加入了推进器模型(TH)反演的重力场结果,可以看出,对于在L1B数据中直接进行处理及在L1A-L1B数据处理中不加入推进器模型,20阶之后所得的重力场结果较差;并且,在L1A-L1B数据处理中加入推进器模型后结果得到改善,但仍与原始结果有差距,说明对于加速度计数据,推进器信号的处理方法会直接影响时变重力场的解算精度。与该方法原理相同的case26为最优策略,即Y轴的频繁校正可能是推进器频繁机动造成的。
|
图 6 去除推进器信号后的大地水准面阶方差 Fig. 6 The degree variance after removing the thruster signal |
本文通过动力学方法,利用2019-01 GRACE-FO卫星实测数据,计算不同加速度计偏差参数校正策略,共计33个算例,并分析对比轨道拟合结果和相应的时变重力场反演结果。轨道拟合作为时变重力场反演的中间步骤,是时变重力场解算的第1步,轨道拟合结果表明,计算的轨道3D残差随校正参数个数的减少而逐渐增大,并在加速度计校正频率相同的情况下,校正参数个数越多轨道残差越小。然而在对时变重力场反演策略进行分析时发现,反演的时变重力场精度与轨道拟合结果没有直接关系,时变重力场解算结果的优劣与加速度计校正策略有关,与加速度计校正参数个数无关。综合分析不同的加速度计校正策略发现,对于加速度计三轴分别采用不同的校正策略会得到不同的结果,其差异主要体现在大于40阶部分,其中Y轴校正参数个数较多时计算结果最优,其原因可能是Y轴为相对不敏感轴,并且由于GRACE-FO卫星装载有激光测距仪,对姿态要求较高,在卫星观测中需频繁对卫星平台进行姿态调整以保证测量精度和星间激光测距精度,而推进器信号耦合至加速度测量时主要作用于YZ平面,因此Y轴需要较多的校正参数。本文研究忽略了加速度计尺度因子,主要因为尺度因子和加速度计参数存在一定的相关性,在GRACE-FO的时变重力场反演中尺度因子通常为每月校正1次[13],而对于尺度因子的选取需要在后续工作中进行进一步研究。
| [1] |
Tapley B D, Bettadpur S, Watkins M, et al. The Gravity Recovery and Climate Experiment: Mission Overview and Early Results[J]. Geophysical Research Letters, 2004, 31(9): L09607
(  0) 0) |
| [2] |
Christophe B, Boulanger D, Foulon B, et al. A New Generation of Ultra-Sensitive Electrostatic Accelerometers for Follow-on and towards the Next Generation Gravity Missions[J]. Acta Astronautica, 2015, 117: 1-7 DOI:10.1016/j.actaastro.2015.06.021
(  0) 0) |
| [3] |
Kornfeld R P, Arnold B W, Gross M A, et al. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-on Mission[J]. Journal of Spacecraft and Rockets, 2019, 56(3): 931-951 DOI:10.2514/1.A34326
(  0) 0) |
| [4] |
王正涛. 卫星跟踪卫星测量确定地球重力场的理论与方法[D]. 武汉: 武汉大学, 2005 (Wang Zhengtao. Theory and Methodology of Earth Gravity Field Recovery by Satellite-to-Satellite Tracking Data[D]. Wuhan: Wuhan University, 2005)
(  0) 0) |
| [5] |
Teixeirada E J, Save H, Tapley B, et al. Accelerometer Parameterization and the Quality of Gravity Recovery and Climate Experiment Solutions[J]. Journal of Spacecraft and Rockets, 2020, 57(4): 740-752 DOI:10.2514/1.A34639
(  0) 0) |
| [6] |
Klinger B, Mayer-Gürr T. The Role of Accelerometer Data Calibration within GRACE Gravity Field Recovery: Results from ITSG-Grace2016[J]. Advances in Space Research, 2016, 58(9): 1 597-1 609 DOI:10.1016/j.asr.2016.08.007
(  0) 0) |
| [7] |
王长青. GRACE时变重力场反演与相关问题研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2015 (Wang Changqing. Time-Variable Gravity Field Determination from GRACE Mission and Some Related Issues[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2015)
(  0) 0) |
| [8] |
冉将军. 低低跟踪模式重力卫星反演理论、方法及应用[D]. 武汉: 中国科学院测量与地球物理研究所, 2013 (Ran Jiangjun. Theory, Methodology and Application of Recovery Using Low-Low Tracking Gravity Satellite Data[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2013)
(  0) 0) |
| [9] |
周浩. 联合多类卫星重力数据反演地球重力场的研究[D]. 武汉: 武汉大学, 2015 (Zhou Hao. Study on the Recovery of the Earth's Gravity Field from the Combination of Multi-Type Satellite Gravimetry Data[D]. Wuhan: Wuhan University, 2015)
(  0) 0) |
| [10] |
Chen Q J, Shen Y Z, Francis O, et al. Tongji-GRACE02s and Tongji-GRACE02k: High-Precision Static GRACE-Only Global Earth's Gravity Field Models Derived by Refined Data Processing Strategies[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(7): 6 111-6 137 DOI:10.1029/2018JB015641
(  0) 0) |
| [11] |
Bettadpur S. Recommendation for A-Priori Bias and Scale Parameter for Level-1B ACC Data[Z]. 2009
(  0) 0) |
| [12] |
吴林冲, 衷路萍, 刘冰石. 点火脉冲对GRACE加速度计校准的影响[J]. 大地测量与地球动力学, 2018, 38(4): 399-401 (Wu Linchong, Zhong Luping, Liu Bingshi. Effect of Pulse Thrusting on GRACE Accelerometers Calibration[J]. Journal of Geodesy and Geodynamics, 2018, 38(4): 399-401)
(  0) 0) |
| [13] |
Dahle C, Flechtner F, Murböck M, et al. GRACE-FO D-103919: GFZ Level-2 Processing Standards[S]. GFZ German Research Centre for Geosciences, 2019
(  0) 0) |
2. University of Chinese Academy of Science, A19 Yuquan Road, Beijing 100049, China;
3. School of Physics, Huazhong University of Science and Technology, 1037 Luoyu Road, Wuhan 430074, China
 2021, Vol. 41
2021, Vol. 41

