2. 应急管理部国家自然灾害防治研究院,北京市安宁庄路1号,100085
因为同震信号会影响震后松弛衰减信号的估计,从重力卫星观测时间序列中准确提取同震重力场变化,既是利用重力卫星数据研究震源机制的基础,又是准确确定地幔粘滞度的基础。有学者采用差分[1]、震前震后平均值差值[2]、堆叠[3]等方法从GRACE的Level 2数据(球谐系数)中提取同震重力变化,但这些方法没有考虑震后松弛信号对同震信号的污染。本文采用美国得克萨斯空间中心(CSR)发布的RL06数据,通过时间序列分析方法提取2004年苏门答腊MW9.3、2010年智利MW8.8和2011年日本东北MW9.0三次俯冲带特大地震的同震重力变化、大地水准面变化、垂线偏差变化及重力梯度变化,并将所得结果与前人根据球体位错理论模型计算的结果[1-8]进行对比。
1 GRACE时间序列分析研究表明[9],RL06模型数据的精度较RL05模型有明显的提升,而不同的RL06模型数据中,CSR发布的RL06模型数据的阶方差最小,其给出了完全规格化的球谐系数,最高阶数为60。本文采用2003-01~2016-09 CSR发布的Level2 RL06 GSM重力场模型数据,受某些因素影响,缺失了16个月的数据。由于GRACE的轨道形状对系数C20项不敏感,该项精度相对较低,本文采用人卫激光测距得到的C20项作为替代[2]。
GRACE重力卫星的轨道高度约为450 km,考虑到重力信号随卫星与地球距离的增大而衰减,重力卫星仅获取了重力场的中长波部分信号。由于受高频噪声的影响,使用GRACE Level2数据直接计算得到的重力场变化呈南北条带效应,很难获得有用的重力变化信息,需要对数据进行平滑处理。Werth等[10]的研究表明,考虑GRACE卫星轨道误差的去相关性滤波器在水文研究中的滤波效果最佳,因此本文采用去相关性的DDK3滤波器进行平滑处理。
GRACE卫星重力场时间序列中包含了趋势、季节、同震和震后等多种信号,需要从这些信息中提取出同震重力变化。本文采用最小二乘拟合时间序列分析方法提取同震信号,对于去除背景场后的GRACE月重力变化时间序列,可用式(1)表示:
| $ \begin{aligned} &\Delta g(t)=a_{0}+a_{1} t+\sum\limits_{k=1}^{n} b_{k} \cos \left(\omega_{k} t+\varphi_{k}\right)+ \\ &c H\left(t-t_{\mathrm{eq}}\right)+d\left[1-\mathrm{e}^{\left(-\frac{t-t_{\mathrm{eq}}}{\tau}\right)}\right] H\left(t-t_{\mathrm{eq}}\right) \end{aligned} $ | (1) |
式中,a0为常数项,a1为线性趋势项,t为相对参考历元时间差,ωk为振幅bk的周期项角频率,φk为对应时期的相位,H(t-teq)为阶跃函数,teq为地震时刻,τ为震后松弛时间(本文取5.0 a),c和d分别为同震和震后重力变化幅度。利用每个月的观测数据,使用最小二乘法求解各项系数。
令
| $ \boldsymbol{x}=\left[\begin{array}{llllll} a_{0} & a_{1} & b_{1} & b_{2} & c & d \end{array}\right]^{\mathrm{T}} $ | (2) |
| $ \boldsymbol{A}= \left[\begin{array}{cccccc} 1 & t_{1} & \cos \left(\omega_{1} t_{1}+\varphi_{1}\right) & \cos \left(\omega_{2} t_{1}+\varphi_{2}\right) & H\left(t_{1}-t_{\mathrm{eq}}\right) & \left.\left[1-\mathrm{e}^{\left(-\frac{t_{1}-t_{\mathrm{eq}}}{\tau}\right.}\right)\right] H\left(t_{1}-t_{\mathrm{eq}}\right) \\ 1 & t_{2} & \cos \left(\omega_{1} t_{2}+\varphi_{1}\right) & \cos \left(\omega_{2} t_{2}+\varphi_{2}\right) & H\left(t_{2}-t_{\mathrm{eq}}\right) & {\left[1-\mathrm{e}^{\left(-\frac{c_{2}-t_{\mathrm{eq}}}{\tau}\right)}\right] H\left(t_{2}-t_{\mathrm{eq}}\right)} \\ \vdots & \cdots & \cdots & \ddots & \cdots & \vdots \\ 1 & t_{n} & \cos \left(\omega_{1} t_{n}+\varphi_{1}\right) & \cos \left(\omega_{2} t_{n}+\varphi_{2}\right) & H\left(t_{n}-t_{\mathrm{eq}}\right) & \left.\left[1-\mathrm{e}^{\left(-\frac{t_{n}-t_{\mathrm{eq}}}{\tau}\right.}\right)\right] H\left(t_{n}-t_{\mathrm{eq}}\right) \end{array}\right] $ | (3) |
式(1)的矩阵形式可写作:
| $ \boldsymbol{ Ax} = \boldsymbol{y} $ |
其法方程为:
| $ {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Ax}} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{y}} $ |
最小二乘解为:
| $ \mathit{\boldsymbol{x}} = {({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}})^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{y}} $ |
式(1)中的c即为同震重力变化。
2 GRACE同震重力场变化2004-12-26苏门答腊地震发生在印度洋板块与缅甸微板块(南亚板块中的微板块)之间;2010-02-27智利地震发生在南极洲板块与美洲板块之间;2011-03-11日本东北地震发生在亚欧板块与太平洋板块的交界处。利用上述数据及方法,在1°×1°的网格上计算2003-01~2016-09去除背景重力场(GGM03S) 后震源区的大地水准面变化、同震重力变化、垂线偏差变化和重力梯度变化的时间序列,并利用时间序列分析提取同震重力场变化信号。
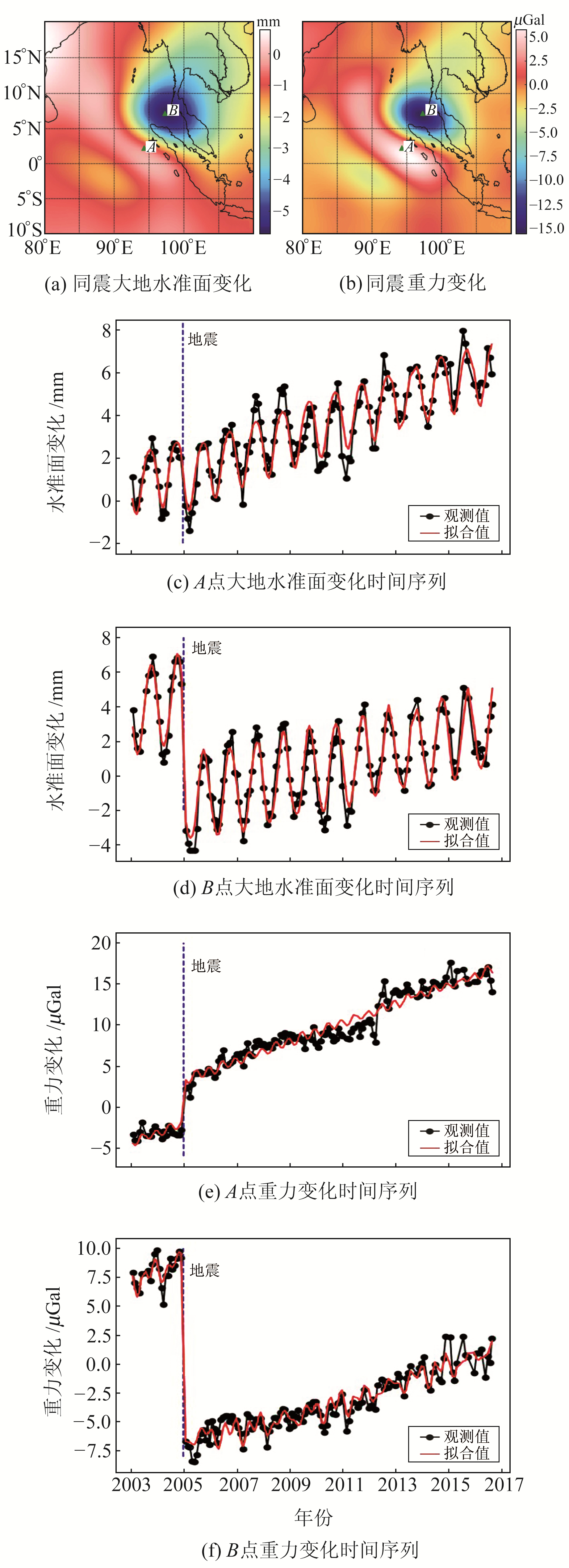
经DDK3平滑处理后,采用最小二乘拟合法分别得到3次地震的同震大地水准面和重力变化。为观察这3次地震引起的重力场变化时间特征,在重力变化最大处选取A、B点进行时间序列分析。苏门答腊、智利和日本东北地震的A、B点坐标分别为(2.75°N,94.25°E)和(7.25°N,97.25°E)、(39.25°S,75.75°W)和(35.25°S,69.25°W)及(38.75°N,138.75°E)和(34.75°N,143.75°E),各点去除背景场后的同震变化时间序列见图 1~3。鉴于地震发生当月信号的复杂性,在时间序列拟合中排除了地震发生当月的数据。根据多项式模型,通过线性最小二乘法拟合了长期趋势、季节、同震和震后引起的重力场变化,其中模型假定震后松弛时间为5.0 a。由图 1~3可见,GRACE观测3次地震的结果均呈正负两极分布,且负变化区(图 1(f)、2(f)、3(e))的同震效应明显大于正变化区(图 1(e)、2(e)、3(f))。由时间序列可知,震后重力与大地水准面变化有明显的指数衰减现象,主要是地幔粘弹性松弛效应引起的。苏门答腊、智利和日本东北地震引起的同震大地水准面变化范围分别为-5.9~0.8 mm、-3.0~0.8 mm和-3.2~0.5 mm;同震重力变化范围分别为-15.5~6.5 μGal、-9.1~2.1 μGal和-11.1~4.2 μGal(表 1)。从图 1(e)中可见,除了2004-12,另一个较为显著的同震信号是2012-04的M8.6和M8.2走滑地震事件引起的,尽管该信号影响2004年震后时间序列的拟合,但并未对2004年同震信号的提取产生干扰。
|
图 1 苏门答腊地震同震变化 Fig. 1 The coseismic variation of the Sumatra earthquake |

|
图 2 智利地震同震变化 Fig. 2 The coseismic variation of the Chile earthquake |

|
图 3 日本东北地震同震变化 Fig. 3 The coseismic variation of the Tohoku earthquake |
|
|
表 1 同震重力场变化范围 Tab. 1 The range of coseismic gravity field varitation |
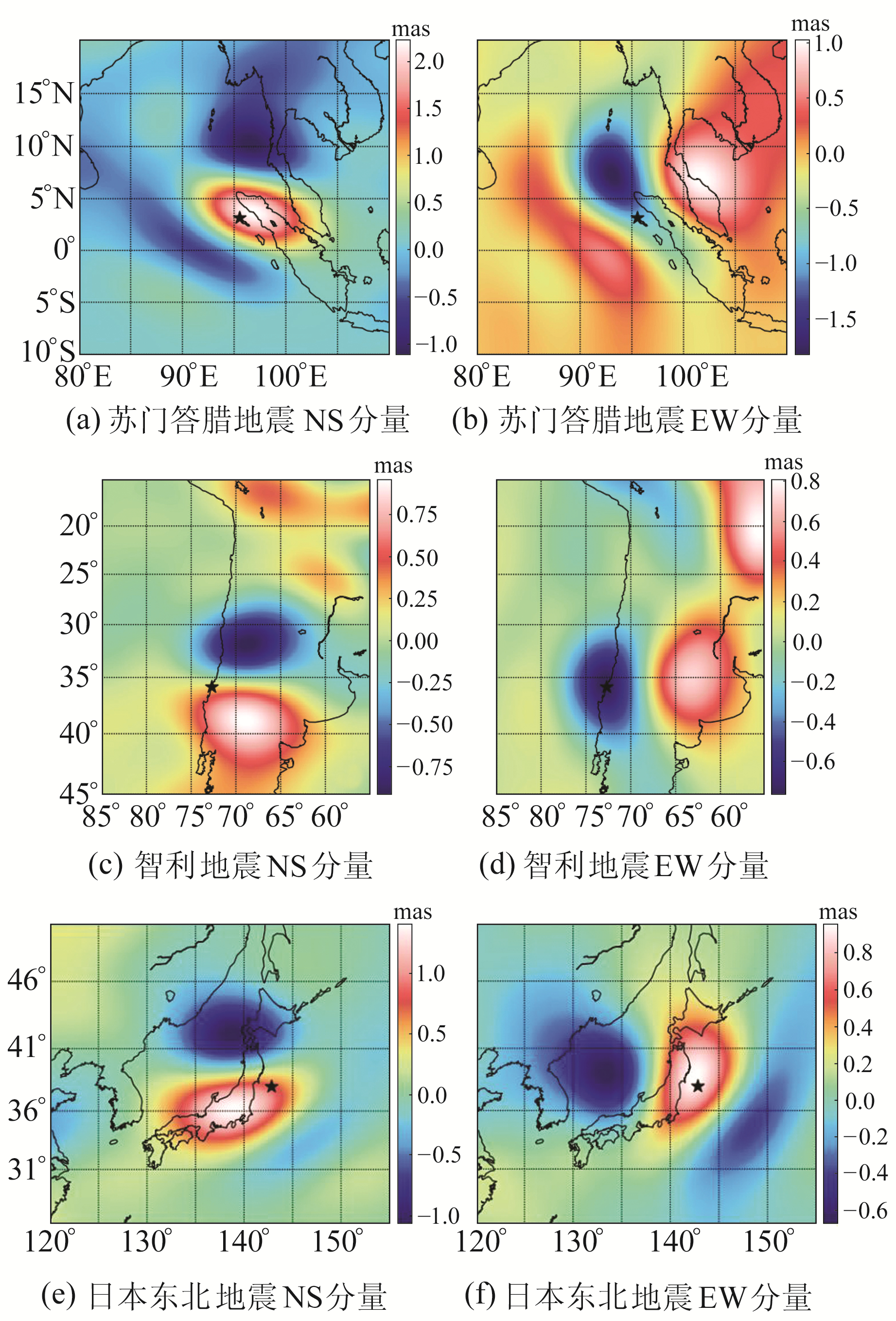
垂线偏差对断层滑动模型较敏感,特别是EW向的垂线偏差,可用于约束地震的震源参数[7-8]。经DDK3平滑处理后,采用最小二乘拟合时间序列分析方法提取3次地震的同震垂线偏差变化空间分布。由图 4可知,GRACE卫星可观测到俯冲带特大地震引起的同震垂线偏差变化,信号呈负-正-负或正-负-正三极分布。苏门答腊、智利和日本东北地震事件引起的同震垂线偏差NS向变化范围分别为-1.2~2.2 mas、-0.9~1.0 mas和-1.1~1.4 mas;EW向变化范围分别为-1.8~1.0 mas、-0.8~0.8 mas和-0.7~ 1.0 mas(表 1)。
|
图 4 同震垂线偏差变化 Fig. 4 Change of coseismic vertical dflection |
计算并提取3次地震的同震重力梯度变化,得到图 5。由图可知,同震重力梯度变化信号呈多极分布,如θλ分量有明显的2对正负对称四象限分布信号。相比于其他重力场物理量,重力梯度有更丰富的地震信号,苏门答腊地震重力梯度rr分量(径向)变化幅度为-0.6~0.4 mE,rθ分量为-0.5~0.3 mE,rλ分量为-0.2~0.4 mE,θθ分量(NS向)为-0.3~0.4 mE,θλ分量为-0.1~0.2 mE,λλ分量(EW向)为-0.3~0.2 mE;智利地震重力梯度rr分量变化幅度为-0.4~0.1 mE,rθ分量为-0.2~0.2 mE,rλ分量为-0.2~0.2 mE,θθ分量为-0.1~0.2 mE,θλ分量为-0.1~0.1 mE,λλ分量为-0.2~0.1 mE;日本东北地震重力梯度rr分量变化幅度为-0.5~0.3 mE,rθ分量为-0.3~0.3 mE,rλ分量为-0.3~0.2 mE,θθ分量为-0.2~0.3 mE,θλ分量为-0.1~0.1 mE,λλ分量为-0.2~0.2 mE。由此可知,重力梯度中rr分量的同震变化幅度最大,rθ分量次之。

|
从左至右分别为rr、rθ、rλ、θθ、θλ和λλ分量 图 5 同震重力梯度变化 Fig. 5 Change of coseismic gravity gradient |
收集理论模型计算的3次地震同震重力场变化,并将其与本文结果进行对比。由表 1可见,利用球体位错理论模型计算的同震重力场变化[1-8]与本文提取的同震重力场分布信号特征一致。对于一个低倾角的俯冲型地震,其上覆板块的变形特征比俯冲板块更显著,即主要变形集中在上覆板块[11](图 6)。因此,发生在上覆板块的同震重力场信号减小的幅度远大于俯冲板块的重力场增加幅度,即可以由海底面、莫霍面升降及内部物质膨胀的模型来解释[12]。震后重力与大地水准面变化均随时间呈非线性增加,这主要是由震后地幔的粘弹性松弛效应引起的。

|
实线和虚线分别表示埋深为10 m和2 km的断层 图 6 Okada弹性位错理论模型[11]计算的倾角为13°、滑动量为1 m的逆冲型地震引起的地表水平和垂直位移 Fig. 6 Theoretical horizontal and vertical displacements due to thrust earthquakes with a dip of 13° and slip of 1 m calculated by Okada's elastic dislocation model[11] |
本文采用最小二乘拟合时间序列分析方法提取的同震重力变化范围均大于前人研究结果[1-4],其中苏门答腊、智利、日本东北地震的差异分别为7 μGal、4 μGal、6 μGal。导致这些差异的因素可能是由于前人采用了CSR RL04或RL05数据,而本文采用更高精度的RL06数据;部分研究采用的是差分[1]、震前震后平均值差值[2]和堆叠[3]方法,而本文采用多项式拟合时间序列分析方法提取同震重力变化;有的研究采用350 km高斯滤波器提取苏门答腊地震重力变化[1]、采用300 km高斯滤波器提取智利地震同震重力变化[2]、采用扇形滤波器提取日本东北地震重力变化[3],而本文均采用DDK3滤波器;震后数据长度不同,震后数据越长,利用时间序列分析方法提取的同震重力变化越精确。
由文献[1-4]给出的球体位错理论模型计算的同震大地水准面变化、重力变化结果与本文的GRACE观测结果均呈正负两极分布。由表 1可见,日本东北地震大地水准面理论值[7]与观测值的差异约为1 mm。在同震重力变化方面,苏门答腊地震的理论值[1]和观测值差异最大约为6.4 μGal,智利地震的理论值[2]与观测值在重力减小区的差异小于1 μGal,日本东北地震的理论值[4]和观测值差异约为1 μGal。考虑到海洋、海潮和大气等模型的不确定性,理论模型计算值与观测值有1~2 μGal的差异是合理的,其中苏门答腊地震理论值与观测值产生较大差异的原因可能是球体位错理论模型中采用的滑动断层模型[12]不同。另外,利用位错理论模型计算同震重力变化需要考虑海水质量重新分布的贡献,如未作这一改正,会影响理论计算的结果。
智利地震同震垂线偏差变化经DDK3平滑后的观测结果与文献[8]在NS向的差异约为0.5 mas,EW向差异约为0.2 mas。日本东北地震同震垂线偏差变化经DDK3平滑后的观测结果与文献[7]在NS向的差异为0.7 mas、EW向差异为0.1 mas。考虑到GRACE类型的重力卫星轨道为近NS向,因此沿NS向的观测精度应高于EW向[7]。NS向垂线偏差产生的差异大于EW向,这是由于智利地震和日本东北地震在理论值计算时分别采用300 km高斯滤波器[8]和350 km高斯滤波器[7],而本文采用DDK3滤波器,因此认为该差异是合理的。
目前很少有计算同震重力梯度变化的理论模型,故无法比较本文时间序列分析方法得到的GRACE同震信号与理论信号的差异。从图 5给出的3个特大俯冲型地震产生的同震重力梯度变化分布来看,其信号特征较大地水准面、重力和垂线偏差更为复杂,即包含更多的信号特征,如θλ分量有明显的2对正负对称四象限分布信号,反映地震造成的地壳密度变化有一个明确的底部。因此,重力梯度可能对某些震源参数更敏感,需要有能够计算同震和震后重力梯度变化的位错模型及用其约束震源参数等方面的研究。
4 结语本文利用DDK3滤波器对GRACE重力卫星的观测数据进行处理,利用最小二乘拟合时间序列分析方法成功提取了2004年苏门答腊、2010年智利和2011年日本东北地震产生的同震重力场变化及其空间分布。苏门答腊地震、智利地震和日本东北地震的同震重力变化范围分别为-15.5~6.5 μGal、-9.1~2.1 μGal和-11.1~4.2 μGal,同震大地水准面变化范围分别为-5.9~0.8 mm、-3.0~0.8 mm和-3.2~0.5 mm;垂线偏差NS向变化范围分别为-1.2~2.2 mas、-0.9~1.0 mas和-1.1~1.4 mas;EW向变化范围分别为-1.8~1.0 mas、-0.8~0.8 mas和-0.7~1.0 mas;重力梯度各分量中,rr分量的同震变化幅度最大,其次为rθ分量。3次地震的同震信号空间分布均表现为:1)同震大地水准面和重力变化信号呈非对称两极分布;2)垂线偏差呈负-正-负或正-负-正三极分布;3)重力梯度变化信号呈复杂的多极分布,如θλ分量有明显的2对正负对称四象限分布信号。通过与位错理论模型计算结果进行比较,验证了本文观测结果与理论计算结果具有较好的一致性,为重力卫星数据在震源机制的计算应用方面提供了可靠的信号提取方法。本文提取的同震重力变化、大地水准面变化、垂线偏差变化和重力梯度变化可为利用重力卫星数据约束震源参数提供新的途径,也可作为GRACE在其他领域(如水文、冰川等)应用的参考。
致谢: 感谢中国科学技术大学胡晓辉博士对本文提出宝贵建议。
| [1] |
张国庆, 付广裕, 周新. 利用GRACE卫星数据提取苏门答腊地震同震和震后重力变化[J]. 大地测量与地球动力学, 2015, 35(2): 303-308 (Zhang Guoqing, Fu Guangyu, Zhou Xin. The Evolution Process of the Gravitational Field after the Sumatra MW9.3 Earthquake from GRACE RL05 Data[J]. Journal of Geodesy and Geodynamics, 2015, 35(2): 303-308)
(  0) 0) |
| [2] |
周新, 孙文科, 付广裕. 重力卫星GRACE检测出2010年智利MW8.8地震的同震重力变化[J]. 地球物理学报, 2011, 54(7): 1 745-1 749 (Zhou Xin, Sun Wenke, Fu Guangyu. Gravity Satellite GRACE Detects Coseismic Gravity Changes Caused by 2010 Chile MW8.8 Earthquake[J]. Chinese Journal of Geophysics, 2011, 54(7): 1 745-1 749)
(  0) 0) |
| [3] |
尹鹏, 张永志, 焦佳爽, 等. 利用GRACE数据检测日本MW9.0地震同震和震后重力变化[J]. 测绘通报, 2018(1): 38-43 (Yin Peng, Zhang Yongzhi, Jiao Jiashuang, et al. Co-seismic and Post-Seismic Gravity Changes of the Japan MW9.0 Earthquake from GRACE RL05 Data[J]. Bulletin of Surveying and Mapping, 2018(1): 38-43)
(  0) 0) |
| [4] |
Zhou X, Sun W K, Zhao B, et al. Geodetic Observations Detecting Coseismic Displacements and Gravity Changes Caused by the MW=9.0 Tohoku-Oki Earthquake[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B5)
(  0) 0) |
| [5] |
Heiskanen W A, Moritz H. 物理大地测量学[M]. 北京: 测绘出版社, 1979 (Heiskanen W A, Moritz H. Physical Geodesy[M]. Beijing: Surveying and Mapping Press, 1979)
(  0) 0) |
| [6] |
Dai C L, Shum C K, Wang R J, et al. Improved Constraints on Seismic Source Parameters of the 2011 Tohoku Earthquake from GRACE Gravity and Gravity Gradient Changes[J]. Geophysical Research Letters, 2014, 41(6): 1 929-1 936 DOI:10.1002/2013GL059178
(  0) 0) |
| [7] |
Sun W K, Zhou X. Coseismic Deflection Change of the Vertical Caused by the 2011 Tohoku-Oki Earthquake(MW9.0)[J]. Geophysical Journal International, 2012, 189(2): 937-955 DOI:10.1111/j.1365-246X.2012.05434.x
(  0) 0) |
| [8] |
Sun W K, Zhou X. Computing Scheme of Co-Seismic Change of Deflection of the Vertical and Applied in the 2010 Chile Earthquake[J]. International Association of Geodesy Symposia, 2014, 139: 269-274
(  0) 0) |
| [9] |
郭飞霄, 孙中苗, 任飞龙, 等. GRACE RL06与RL05时变重力场模型数据初步比较分析[J]. 大地测量与地球动力学, 2020, 40(5): 546-550 (Guo Feixiao, Sun Zhongmiao, Ren Feilong, et al. Preliminary Comparative Analysis of GRACE RL06 and RL05 Time-Variable Gravity Models[J]. Journal of Geodesy and Geodynamics, 2020, 40(5): 546-550)
(  0) 0) |
| [10] |
Werth S, Güntner A, Schmidt R, et al. Evaluation of GRACE Filter Tools from a Hydrological Perspective[J]. Geophysical Journal International, 2010, 179(3): 1 499-1 515
(  0) 0) |
| [11] |
Okada Y. Surface Deformation Caused by Shear and Tensile Faults in a Half-Space[J]. Bulletin of the Seismological Society of America, 1985, 75(4): 1 135-1 154 DOI:10.1785/BSSA0750041135
(  0) 0) |
| [12] |
Han S C, Shum C K, Bevis M, et al. Crustal Dilatation Observed by GRACE after the 2004 Sumatra-Andaman Earthquake[J]. Science, 2006, 313(5 787): 658-662
(  0) 0) |
2. 2 National Institute of Natural Hazards, MEM, 1 Anningzhuang Road, Beijing 100085, China
 2021, Vol. 41
2021, Vol. 41


