2. 中国地震局地震大地测量重点实验室,武汉市洪山侧路40号,430071;
3. 湖北省地震局,武汉市洪山侧路48号,430071
地震预测的难度在于地球内部的不可入性、地震的非频发性及地震发生机理的复杂性。科学合理地进行地震数据预测,对于救灾物资的有效配置及国计民生具有重要的指导意义[1-3]。随着计算机硬件设备和智能算法的发展,利用计算机的高速计算能力和智能学习算法对地震活动进行建模预测成为地震预测领域的主流研究方向。现今的地震预测领域已成为横跨多门基础学科的综合研究领域[4],有学者利用机器学习算法从储层预测、地震灾害信息预测、地震死亡人数评估等方面进行研究[5-8],并采用统计学方法和机器学习方法对股票价格进行建模预测[9-10]。
目前地震数据预测仍面临诸多问题,如当预测时间和地理区域范围较大时,特征指标数据不能很好地描述地震的发生状况,预测性能较差;神经网络等需要训练的算法,需要大量的异常数据集进行训练,否则容易出现过拟合问题。针对这些问题,本文提出一种基于核混合效应的回归模型,并应用于湖北地震台站地球物理数据的预测仿真,结果表明,相较于传统的神经网络机器学习算法,该模型预测效果较好,预测精度较高[11-12]。
1 核混合效应回归模型 1.1 最小二乘支持向量机与线性混合模型内核提供了一种有效的方法来制定基于内部乘积的线性算法的非线性概括,基于内核的学习已越来越多地用于各个学科的数据分析程序中。支持向量机(SVM)是一种受监督的基于内核的算法,可用于分类和回归应用程序。SVM找到约束优化问题的解,该解以原始形式用非线性特征映射函数φ(x)表示,通过引入拉格朗日乘数和满足Mercer条件的核函数K(xi, xj)=φ(xi)Tφ(xj),可将原始形式转换为通常更易于求解的对偶形式。
最近引入了最小二乘支持向量机(LS-SVM)作为经典SVM分类器的一种变体,其中不等式约束由等式约束代替,这种重构允许通过将相应的凸二次规划问题简化为线性方程组来解决SVM问题。除了提供简单的软件实现和增加数值稳定性外,这种方法还可将经典的SVM扩展到解决数据分析和模式识别中的更多问题。
使用内核可以通过在特征空间中执行岭回归来解决回归问题。给定代表N点坐标的输入矩阵X∈RN×d、d维空间中的x1, x2, …, xN和对应的输出向量y∈RN×1,并假设每个观测值都与对应的输入有关。
| $ \boldsymbol{y}_{i}=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\varphi}\left(x_{i}\right)+b+e_{i}, i=1,2, \cdots, N $ | (1) |
式中,yi为输出向量观测值,φ(xi)为输入矩阵的坐标,wT、b、ei为约束条件参数。
通过最小化目标函数
| $ f(x)=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\varphi}(x)+b $ | (2) |
在式(1)中给出的N个约束条件下,使用惩罚参数γ。格朗日函数写为:
| $ \begin{gathered} L(\boldsymbol{w}, b, \boldsymbol{e}, \boldsymbol{\alpha})=\frac{1}{2} \boldsymbol{w}^{\mathrm{T}} \boldsymbol{w}+\frac{\gamma}{2} \boldsymbol{e}^{\mathrm{T}} \boldsymbol{e}- \\ \sum\limits_{i=1}^{N} \alpha_{i}\left[\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\varphi}\left(x_{i}\right)+b+e_{i}-y_{i}\right] \end{gathered} $ | (3) |
式中,αi(i=1, …, N)为拉格朗日乘数,e=[e1, e2, …, eN]T,α=[α1, α2, …, αN]T。通过定位静止点找到w、b、ei、αi的最佳值,即为式(3)的拉格朗日函数点。使用S=[φ(x1), φ(x2), …, φ(xN)]T,最优条件可总结为:
| $ \left[\begin{array}{cccc} \boldsymbol{I}_{k} & {\bf{0}}_{k} & {\bf{0}}_{k \times N} & -\boldsymbol{S}^{\mathrm{T}} \\ {\bf{0}}_{k}^{\mathrm{T}} & 0 & {\bf{0}}_{N}^{\mathrm{T}} & {\bf{1}}_{N}^{\mathrm{T}} \\ {\bf{0}}_{N \times k} & {\bf{0}}_{N} & \gamma \boldsymbol{I}_{N} & -\boldsymbol{I}_{N} \\ \bf{S} & {\bf{1}}_{N} & \boldsymbol{I}_{N} & {\bf{0}}_{N} \end{array}\right]\left[\begin{array}{c} \boldsymbol{w} \\ b \\ \boldsymbol{e} \\ \boldsymbol{\alpha} \end{array}\right]=\left[\begin{array}{c} {\bf{0}}_{k} \\ 0 \\ {\bf{0}}_{N} \\ \boldsymbol{y} \end{array}\right] $ | (4) |
式中,Ip为大小为p的恒等矩阵,0p×q为0的p×q维矩阵,1p和0p分别为1和0的p×1维向量,k为特征空间的维数。消除向量w和e得到:
| $ \left[\begin{array}{cc} 0 & {\bf{1}}_{N}^{\mathrm{T}} \\ {\bf{1}}_{N} & \boldsymbol{\varOmega}+\left(\frac{1}{\gamma}\right) \boldsymbol{I}_{N} \end{array}\right]\left[\begin{array}{c} b \\ \boldsymbol{\alpha} \end{array}\right]=\left[\begin{array}{c} 0 \\ \boldsymbol{y} \end{array}\right] $ | (5) |
式中,Ω=SST为大小为N×N维的核矩阵,Ωij=K(xi, xj)。如果式(5)中的矩阵是可逆的,则b和α 可以唯一确定,表示计算量
| $ \hat{\boldsymbol{f}}\left(x_{*}\right)=\sum\limits_{i=1}^{N} \hat{\alpha}_{i} \boldsymbol{K}\left(x_{*}, x_{i}\right)+\hat{b} $ | (6) |
线性混合模型的观测值可以写为:
| $ \boldsymbol{y}=\boldsymbol{X} \boldsymbol{\beta}+\boldsymbol{Z} \boldsymbol{u}+\boldsymbol{e} $ | (7) |
式中,y为观测向量,β为固定效应向量(其中包括一个常数项),u~N(0, G)为未观察到的随机效应向量,e~N(0, R)为随机误差的向量,X和Z分别为固定效应和随机效应设计矩阵。向量 u和e不相关,u和y的联合密度最大化:
| $ \begin{gathered} p(\boldsymbol{u}, \boldsymbol{y} \mid \boldsymbol{\beta}, \boldsymbol{G}, \boldsymbol{R}) \propto \\ \exp \left\{-\frac{1}{2}\left[\boldsymbol{e}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{e}+\boldsymbol{u}^{\mathrm{T}} \boldsymbol{G}^{-1} \boldsymbol{u}\right]\right\} \end{gathered} $ | (8) |
产生亨德森的混合模型方程式(MME):
| $ \left[\begin{array}{c} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{X} & \boldsymbol{X}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{Z} \\ \boldsymbol{Z}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{X} & \boldsymbol{Z}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{Z}+\boldsymbol{G}^{-1} \end{array}\right]\left[\begin{array}{c} \hat{\boldsymbol{\beta}} \\ \hat{\boldsymbol{u}} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{y} \\ \boldsymbol{Z}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{y} \end{array}\right] $ | (9) |
式中,
考虑一个包含N次地震记录的数据集,数据集中记录的总数为
| $ \begin{gathered} \boldsymbol{y}_{i j}=\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{x}_{i j}+\boldsymbol{h}\left(\boldsymbol{s}_{i j}\right)+\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{z}_{i j}+\boldsymbol{e}_{i j}, \\ i=i: N, j=i: n_{i} \end{gathered} $ | (10) |
式中,yij为与第i次地震的第j次记录相对应的目标变量,xij为固定效应协变量矢量,β为固定效应矢量,sij为包含与目标变量没有特定关系的预测变量的矢量,zij为随机效应协变量向量,ui为随机效应向量,eij为与yij相关的随机误差项。向量β包含常数项作为其第1项,向量 xij的第1项为1。假定向量ui和ei=[ei1, ei2, …, ein]T遵循正态分布,分别具有均值零和协方差矩阵Gi和Ri,向量ui和ei不相关,则式(10)可用矩阵形式写为:
| $ \boldsymbol{y}=\boldsymbol{X} \boldsymbol{\beta}+\boldsymbol{\varOmega} \boldsymbol{\alpha}+\boldsymbol{Z} \boldsymbol{u}+\boldsymbol{e} $ | (11) |
式中,y为Nn×1维向量,αi~N(0, Ai)为通过堆叠αij获得的拉格朗日乘子的向量,X为矩阵堆叠 xijT,Ω为核矩阵,G、R和A是分别定义为 G=diag(G1, G2, …, GN)、R=diag(R1, R2, …, RN)和A=diag(A1, A2, …, AN)的块对角矩阵。给定协方差矩阵G、A和R,通过最大化对数似然来找到 β、u和α的最佳值:
| $ \begin{gathered} \boldsymbol{l}(\boldsymbol{\beta}, \boldsymbol{u}, \boldsymbol{\alpha})=-\frac{1}{2}\left[(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\beta}-\boldsymbol{Z} \boldsymbol{u}-\boldsymbol{\varOmega} \boldsymbol{\alpha})^{\mathrm{T}}\right.\cdot \\ \left.\boldsymbol{R}^{-1}(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\beta}-\boldsymbol{Z} \boldsymbol{u}-\boldsymbol{\varOmega} \boldsymbol{\alpha})+\boldsymbol{u}^{\mathrm{T}} \boldsymbol{G}^{-1} \boldsymbol{u}+\boldsymbol{\alpha}^{\mathrm{T}} \boldsymbol{A}^{-1} \boldsymbol{\alpha}\right] \end{gathered} $ | (12) |
设定l(β, u, α)关于β、u和α的偏导数为零,则得出以下方程组:
| $ \begin{array}{c} {\left[\begin{array}{ccc} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{X} & \boldsymbol{X}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{Z} & \boldsymbol{X}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{\varOmega} \\ \boldsymbol{Z}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{X} & \boldsymbol{Z}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{Z}+\boldsymbol{G}^{-1} & \boldsymbol{Z}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{\varOmega} \\ \boldsymbol{\varOmega}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{X} & \boldsymbol{\varOmega}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{Z} & \boldsymbol{\varOmega}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{\varOmega}+\boldsymbol{A}^{-1} \end{array}\right] \cdot} \\ {\left[\begin{array}{c} \hat{\boldsymbol{\beta}}\\ \hat{\boldsymbol{u}}\\ \hat{\boldsymbol{\alpha}} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{y} \\ \boldsymbol{Z}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{y} \\ \boldsymbol{\varOmega}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{y} \end{array}\right]} \end{array} $ | (13) |
在前面的推导中,假设协方差矩阵G、A和R是已知的,并且已选择具有相关参数的适当核函数。但在大多数实际情况下,协方差矩阵和核函数必须由用户确定,可以使用多种方法来估计这3个协方差矩阵,例如最小化广义交叉验证得分法或最大化残差最大似然(REML)法。一旦确定了 G、A、R和 Ω,就可利用式(13)确定固定效应、随机效应和拉格朗日乘数的最佳值,并将其代入式(11)。模型对(x(i), s(i), z(i))描述的第i个观测点的估计为:
| $ \begin{gathered} E\left[y^{(i)} \mid x^{(i)}, s^{(i)}, z^{(i)}\right]= \\ x^{(i)} \hat{\boldsymbol{\beta}}+\sum\limits_{j=1}^{N_{n}} \boldsymbol{K}\left(s^{(i)}, s^{(j)}\right) \hat{\alpha}_{j}+z^{(i)} \hat{\boldsymbol{u}} \end{gathered} $ | (14) |
未观测点(x*, s*)的预测方程为:
| $ E\left[y_{*} \mid x_{*}, s_{*}\right]=x_{*} \hat{\boldsymbol{\beta}}+\sum\limits_{j=1}^{N_{n}} \boldsymbol{K}\left(s_{*}, s^{(j)}\right) \hat{\alpha}_{j} $ | (15) |
由于对条件期望的核估计可能存在偏差,因此必须注意以正确置信区间为中心。假设观测值可以写成均值函数f(x)和标准偏差函数σ(x):
| $ y_{i}=f\left(x_{i}\right)+\sigma\left(x_{i}\right) \varepsilon_{i}, i=1,2, \cdots, n $ | (16) |
其中,E[εi|xi]=0, var[εi|xi]=1,以x为条件的期望和方差为E[y|x]=f(x)、var[y|x]=σ2(x)。f(x)的100(1-a)%置信区间对应于边界qa:
| $ P\left(|\hat{f}(x)-f(x)| \leqslant q_{a}\right) \geqslant 1-a $ | (17) |
其中,P(·)表示概率。
可以证明式(17)为最小二乘支持向量机器模型,式(6)为线性平滑器。也就是说,存在一个向量L(x)=[l1(x), l2(x), …, ln(x)]T。
| $ \hat{f}(x)=\sum\limits_{i=1}^{n} l_{i}(x) y_{i} $ | (18) |
估计量
| $ E\left[\hat{f}(x) \mid x=x_{*}\right]=\sum\limits_{i=1}^{n} l_{i}(x) f\left(x_{i}\right) $ | (19) |
| $ \operatorname{var}\left[\hat{f}(x) \mid x=x_{*}\right]=\sum\limits_{i=1}^{n} l_{i}(x)^{2} \sigma^{2}\left(x_{i}\right) $ | (20) |
对于式(19),
| $ \begin{gathered} \operatorname{bias}\left[\hat{f}(x) \mid x=x_{*}\right]= \\ \sum\limits_{i=1}^{n} l_{i}(x) f\left(x_{i}\right)-f\left(x_{*}\right) \end{gathered} $ | (21) |
可以使用估算器近似为:
| $ \hat{\operatorname{bias}}\left[\hat{f}(x) \mid x=x_{*}\right]=\boldsymbol{L}^{\mathrm{T}}\left(x_{*}\right) \hat{\boldsymbol{F}}-\hat{f}\left(x_{*}\right) $ | (22) |
式中,
| $ \hat{\operatorname{var}}\left[\hat{f}(x) \mid x=x_{*}\right]=\boldsymbol{L}^{\mathrm{T}}\left(x_{*}\right) \hat{\boldsymbol{\varSigma}} \boldsymbol{L}\left(x_{*}\right) $ | (23) |
式中,Σ为由训练点处的预测方差组成的对角矩阵。使用式(22)和式(23)得到条件均值的近似及偏差校正的100(1-a)%点状置信区间为:
| $ \begin{gathered} \hat{f}\left(x_{*}\right)-\hat{\operatorname{bias}}\left[\hat{f}(x) \mid x=x_{*}\right] \pm\\ z_{1-\frac{\alpha}{2}} \sqrt{\hat{\operatorname{var}}\left[\hat{f}(x) \mid x=x_{*}\right]} \end{gathered} $ | (24) |
式中,
| $ \begin{gathered} \hat{f}\left(x_{*}\right)-\hat{\operatorname{bias}}\left[\hat{f}(x) \mid x=x_{*}\right] \pm \\ z_{1-\frac{\alpha}{2}} \sqrt{\hat{\sigma}^{2}\left(x_{*}\right)+\hat{\operatorname{var}}\left[\hat{f}(x) \mid x=x_{*}\right]} \end{gathered} $ | (25) |
式中,
对于本文得出的半参数模型,第i个观测值由3种类型的预测变量
| $ \begin{array}{c} \boldsymbol{L}(\tilde{x})=x^{(i)} \boldsymbol{U} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{V}^{-1}+\left(\boldsymbol{\varOmega}^{(i)} \boldsymbol{A} \boldsymbol{\varOmega} \boldsymbol{V}^{-1}+\right. \\ \left.z^{(i)} \boldsymbol{G} \boldsymbol{Z}^{\mathrm{T}}\right)\left(\boldsymbol{I}_{N_{n}}-\boldsymbol{X}^{\mathrm{T}} \boldsymbol{U} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{V}^{-1}\right) \end{array} $ | (26) |
式中,U=(XTV-1X)-1和Ω(i)为矩阵Ω的第i行。为了评估新点
| $ \begin{gathered} \boldsymbol{L}\left(\tilde{x}^{*}\right)=x^{(i)} \boldsymbol{U} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{V}^{-1}+ \\ \boldsymbol{\varOmega}_{*} \boldsymbol{A} \boldsymbol{\varOmega} \boldsymbol{V}^{-1}\left(\boldsymbol{I}_{N_{n}}-\boldsymbol{X}^{\mathrm{T}} \boldsymbol{U} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{V}^{-1}\right) \end{gathered} $ | (27) |
式中,Ω*=[K(s*, s1), K(s*, s2), …, K(s*, sNn]。
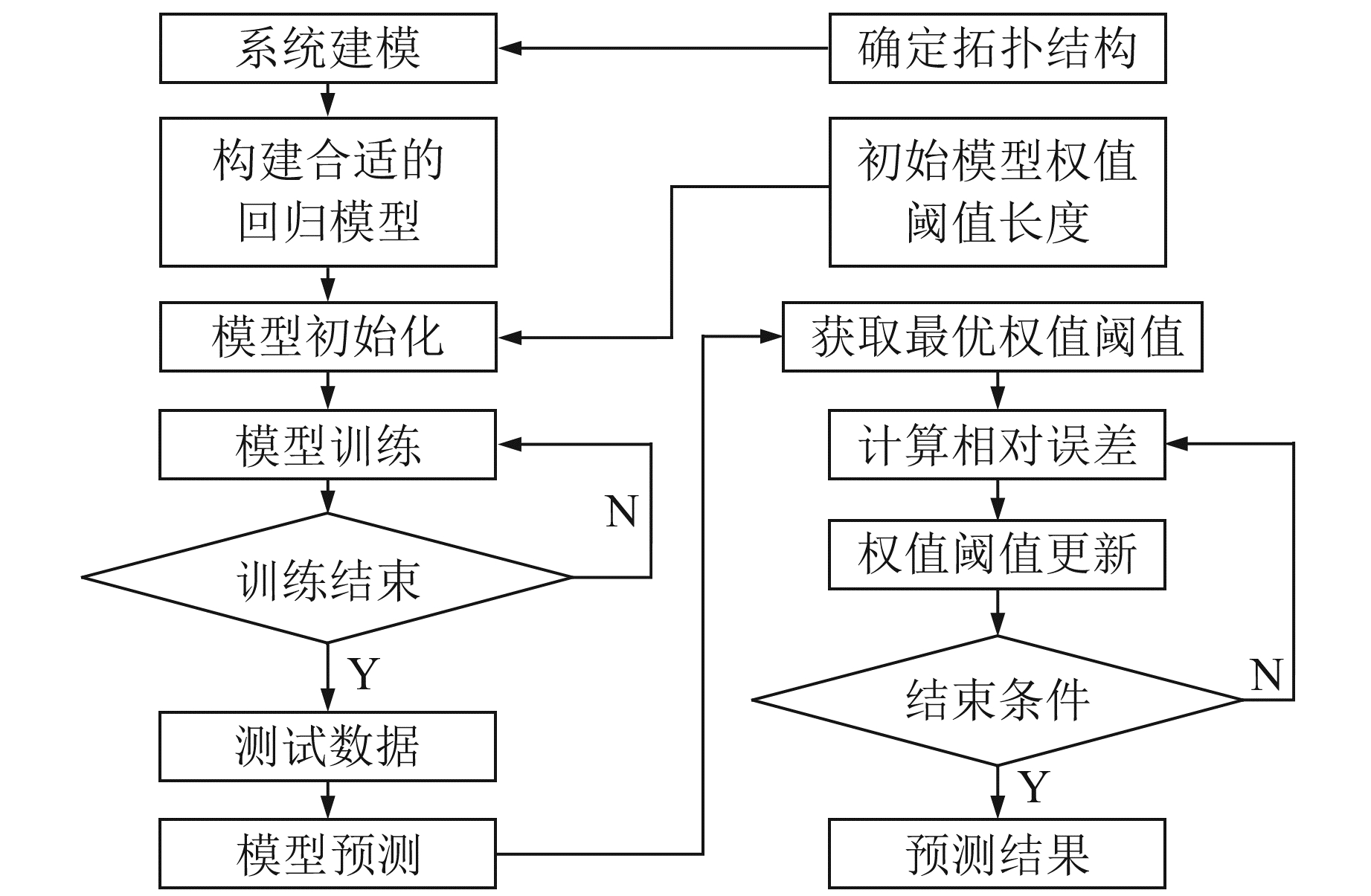
以上算法在MATLAB 9.0软件上测试通过,算法流程见图 1。
|
图 1 算法流程 Fig. 1 Algorithm flowchart |
为验证本文模型算法的可行性和准确性,选用地震地球物理观测数据在此算法基础上开展仿真实验,并与传统的经典神经网络算法实例作比较。首先选取水温分钟观测值训练该神经网络模型,用训练数据进化200次,训练过程中神经网络模型预测误差变化趋势见图 2。

|
图 2 网络进化过程 Fig. 2 Network evolution |
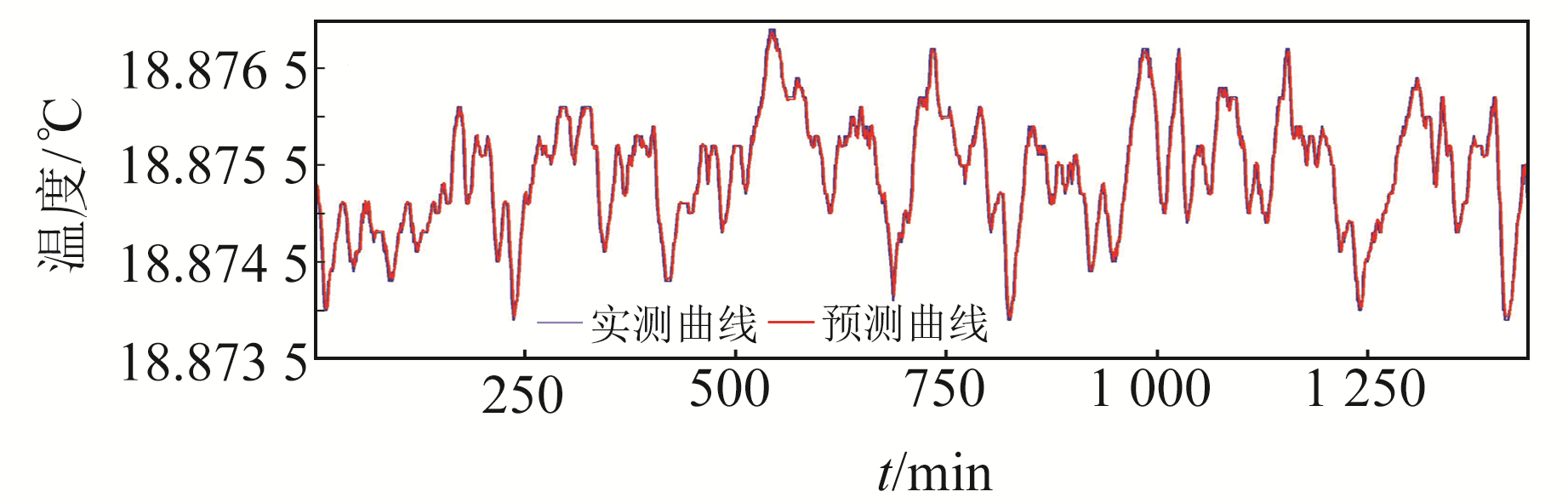
当训练次数达到200次时,预测误差小于2.37×10-3,达到训练要求的目标误差0.01。随机选取2020-10-11湖北省荆门地震台4测点的水温仪实测时序数据作为测试数据,图 3为BP神经网络预测、RBF神经网络预测、模糊神经网络预测及线性神经网络预测结果对比,图 4为基于核混合效应回归模型预测。

|
图 3 几种神经网络预测算法的预测结果(荆门) Fig. 3 Prediction results of several neural network prediction algorithms(Jingmen) |
|
图 4 基于核混合效应回归模型的预测结果(荆门) Fig. 4 Prediction results of regression model prediction based on nuclear mixed effects(Jingmen) |
由图 3和图 4可知,本文回归模型预测效果较好,其预测曲线的拟合度明显高于其他算法。BP神经网络预测、RBF神经网络预测、模糊神经网络预测、线性神经网络预测及基于核混合效应回归模型预测的相对误差分别为0.92%、0.83%、0.78%、0.54%、0.05%,本文算法模型的相对误差曲线见图 5,其他几种算法的相对误差曲线类似,不再赘述。

|
图 5 基于核混合效应回归模型预测的相对误差(荆门) Fig. 5 Predicting relative error based on the regression model of nuclear mixed effects(Jingmen) |
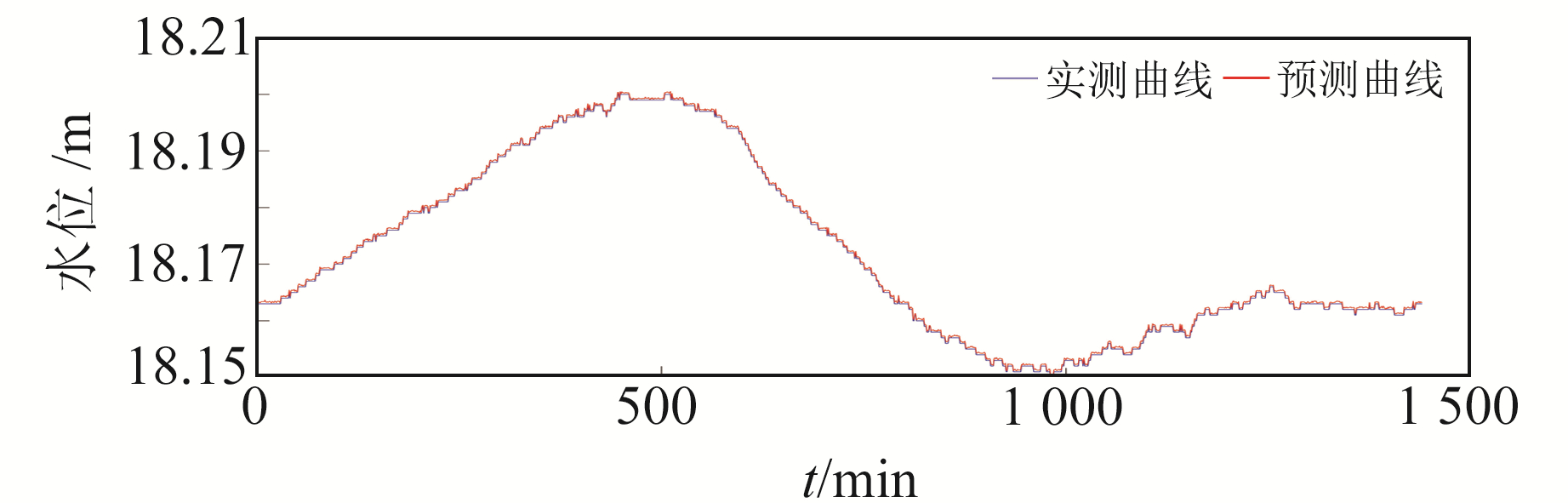
同理,选取2020-09-24湖北省房县三海村地震台1测点水位仪实测时序数据,结合上述5种神经网络算法进行仿真实验,结果见图 6~7。

|
图 6 几种神经网络预测算法的预测结果(房县) Fig. 6 Prediction results of several neural network prediction algorithms(Fangxian) |
|
图 7 基于核混合效应回归模型的预测结果(房县) Fig. 7 Prediction results of regression model prediction based on nuclear mixed effects(Fangxian) |
经计算,对于水位数据预测而言,BP神经网络预测、RBF神经网络预测、模糊神经网络预测、线性神经网络预测及基于核混合效应回归模型预测的相对误差分别为2.26%、1.78%、1.59%、1.34%、0.48%,其中基于核混合效应回归模型预测的相对误差曲线见图 8。对于其他地球物理观测手段(形变、重力、电磁等)产出的观测数据资料,分析方法相同。

|
图 8 基于核混合效应回归模型预测的相对误差(房县) Fig. 8 Predicting relative error based on the regression model of nuclear mixed effects(Fangxian) |
本文提出一种基于核混合效应回归模型的数据预测新方法,并将该方法用于地震地球物理观测数据的预测。对不同神经网络算法进行仿真实验对比,结果表明,本文算法能很好地预测未来曲线趋势,且相对误差较低。结论如下:
1) 本文方法使用最小二乘支持向量机来扩展线性混合模型方程,该扩展为复杂关系的建模提供了灵活的工具,同时考虑到观测值之间的相关性,提出的方法在计算上是有效的,其将优化问题简化为线性方程组。
2) 当前常用的参数最小二乘法是普通最小二乘模型的扩展,该模型旨在用于线性模型。对于线性模型,已知最小二乘估计量是无偏的,并且在所有线性无偏估计量中方差最低,但像LS-SVM估计器这样的有偏估计器可能会比最小二乘估计器获得更低的均方误差。
3) 通过仿真研究,假设线性数据生成函数,并将本文方法与参数最小二乘法的精度进行比较,仿真结果表明,使用本文模型可以更好地处理涉及相关预测变量的问题。关于LS-SVM的许多结论都适用于非线性模型,这是因为LS-SVM使用非线性核处理非线性问题,并且一旦选择了核,LS-SVM模型就相当于分配给每个点的权重保持线性。
4) 本文模型算法还可应用于地震地球物理其他测项(地磁、形变、重力等)的数据预测,应用前景广泛,同时也可为较复杂的深度学习类算法框架模型的构建提供实践基础。
| [1] |
张研, 邝贺伟. 地震震级预测的相关向量机模型[J]. 世界地震工程, 2020, 36(1): 212-221 (Zhang Yan, Kuang Hewei. Relevance Vector Machine Model for Earthquake Magnitude Prediction[J]. World Earthquake Engineering, 2020, 36(1): 212-221)
(  0) 0) |
| [2] |
王晨晖, 刘立申, 任佳, 等. 主成分分析法和遗传算法优化的支持向量机模型在地震伤亡人数预测中的应用[J]. 地震, 2020, 40(3): 142-152 (Wang Chenhui, Liu Lishen, Ren Jia, et al. Application of Support Vector Machine Model Optimized by Principal Component Analysis and Genetic Algorithm in the Prediction of Earthquake Casualties[J]. Earthquake, 2020, 40(3): 142-152)
(  0) 0) |
| [3] |
Yu H, Qiang M, Liu S Q. Territorial Suitability Assessment and Function Zoning in the Jiuzhaigou Earthquake-Stricken Area[J]. Journal of Mountain Science, 2019, 16(1): 195-206 DOI:10.1007/s11629-017-4741-0
(  0) 0) |
| [4] |
周天祥. 基于特异性免疫机制的地震预测模型[D]. 武汉: 武汉大学, 2019 (Zhou Tianxiang. The Earthquake Prediction Model Based on the Adaptive Immune Mechanism[D]. Wuhan: Wuhan University, 2019)
(  0) 0) |
| [5] |
鲍彬彬. 基于地震数据的储层预测自动寻优模型研究[D]. 厦门: 厦门大学, 2017 (Bao Binbin. Research on Reservior Prediction Automatic Optimization Model Based on Seismic Data[D]. Xiamen: Xiamen University, 2017)
(  0) 0) |
| [6] |
景国勋, 邢丽华, 邓奇根. 基于PCA-ELM的地震死亡人数评估[J]. 安全与环境学报, 2020, 20(2): 617-623 (Jing Gouxun, Xing Lihua, Deng Qigen. Evaluation of the Earthquake Death Toll Based on the PCA-ELM Analysis[J]. Journal of Safety and Environment, 2020, 20(2): 617-623)
(  0) 0) |
| [7] |
魏赛拉加, 辛倩男, 隋嘉, 等. 青海地区环境的地震灾害信息预测模型研究[J]. 华南地震, 2019, 39(4): 40-45 (Wei Sailajia, Xin Qiannan, Sui Jia, et al. Research on Earthquake Disaster Information Prediction Model of Qinghai Region[J]. South China Journal of Seismology, 2019, 39(4): 40-45)
(  0) 0) |
| [8] |
Naik P P S, Gopal T V. Particle Swarm Optimization(PSO) Based K-Means Image Segmentation Algorithm[J]. International Journal of Scientific Research, 2016, 5(1)
(  0) 0) |
| [9] |
Xiong R X, Nichols E P, Shen Y. Deep Learning Stock Volatility with Google Domestic Trends[EB/OL]. https://arxiv.org/abs/1512.04916v3, 2016
(  0) 0) |
| [10] |
Selvin S, Vinayakumar R, Gopalakrishnan E A, et al. Stock Price Prediction Using LSTM, RNN and CNN-Sliding Window Model[C]. International Conference on Advances in Computing, Dehradun, 2017
(  0) 0) |
| [11] |
Tezcan J, Hazirbaba Y D, Cheng Q. A Kernel-Based Mixed Effect Regression Model for Earthquake Ground Motions[J]. Advances in Engineering Software, 2018, 120: 26-35 DOI:10.1016/j.advengsoft.2016.06.002
(  0) 0) |
| [12] |
顾艳春. MATLAB R2016a神经网络设计应用27例[M]. 北京: 电子工业出版社, 2018 (Gu Yanchun. Design and Application of MATLAB r2016a Neural Network[M]. Beijing: Publishing House of Electronics Industry, 2018)
(  0) 0) |
2. Key Laboratory of Earthquake Geodesy, CEA, 40 Hongshance Road, Wuhan 430071, China;
3. Hubei Earthquake Agency, 48 Hongshance Road, Wuhan 430071, China
 2021, Vol. 41
2021, Vol. 41

