随着卫星重力测量技术的发展,利用重力卫星观测数据反演地球重力场已成为普遍的重力场研究手段[1]。针对重力卫星观测特点,众多学者提出不同的重力场反演方法,总体上分为空域法和时域法[2],时域法又可分为能量守恒方法[3-5]、短弧法[1, 6-8]、动力学法[9]等。时域法反演地球重力场时,在处理海量观测数据、获取观测方程以及构建并解算法方程的过程中存在计算量巨大、计算耗时长的问题[10]。针对以上问题,许多学者基于并行计算平台,分析反演方法的并行潜力,设计了并行算法,以提高计算效率。文献[10]总结并行技术提高反演效率的关键任务,提出了OpenMP并行算法;文献[11]实现了OpenMP并行快速解算重力场模型,反演得到60阶模型,解算耗时减少75%;文献[12-13]在曙光集群高性能计算系统上实现了MPI并行算法,解算120、240阶模型时,法矩阵求逆耗时仅为229 s、7 359 s,解算总耗时分别为40 min、7 h;文献[14]综合OpenMP和MKL(Math Kernel Library)库二者优势,有效提高了反演效率;文献[15]分析基于超级计算机平台的并行技术应用于卫星重力测量的相关问题。
现今,反演重力场的并行算法研究主要针对OpenMP、MPI等CPU同构并行展开,存在并行算法硬件需求高、未充分挖掘反演方法并行潜力的问题。随着GPU(graphic processing unit)的发展,GPU单个核心运算能力和芯片核心集成数量都得到大幅提升,CPU+GPU组成的异构并行结构成为常见的异构并行运算平台,单台个人电脑即可构成其主体部分。相较于CPU,GPU具有多核心、高集成的特点,能够同时开辟上千条线程进行运算,从而实现密集运算的高度并行化。
基于以上分析,本文针对卫星跟踪卫星观测模式,在能量守恒方法的基础上,提出一种重力场反演快速异构并行算法(后文简称快速反演算法),利用CUDA在GPU端实现了并行计算观测方程设计矩阵与自由项向量,结合MKL库与分区平差法[16]、预处理共轭梯度法[17]在CPU端完成了低内存消耗下的法方程的快速构建和解算。用该算法处理GRACE-FO卫星2020-01-01~06-30期间共13.77 GB观测数据,反演获得120阶重力场模型GM-GraceFO2020h(GM为gravity model缩写,后缀GraceFO表示解算采用GRACE-FO数据,2020代表所用数据年份,h为heterogeneous parallelism的首字母),并与现有GRACE模型和算法相对比。结果表明,快速反演算法所得模型与现有模型精度相当,且相较于传统串行算法,反演耗时减少98.479%,内存消耗减小1个量级。算法在保证反演精度的同时,能有效提高计算效率,缩短反演时间,降低对计算平台的硬件需求,可以为大规模处理卫星重力数据提供经济、高效的实施方案。
1 能量守恒方法原理能量守恒方法反演地球重力场,在惯性系下可得单星能量守恒积分式[5]:
| $ \begin{gathered} T-E_{0}=\frac{1}{2} \dot{\boldsymbol{r}}^{2}-\omega\left(r_{x} \dot{r}_{y}-r_{y} \dot{r}_{x}\right)- \\ \int \dot{\boldsymbol{r}} \boldsymbol{f}_{\mathrm{non}} \mathrm{d} t-U_{0}-V_{\mathrm{conv}} \end{gathered} $ | (1) |
式中,T为扰动位;E0为积分常量,对应一个积分弧段;等号右侧第1项为动能,
| $ \begin{gathered} V_{\text {conv }}=V_{\text {solar-tide }}+V_{\text {lunar-tide }}+V_{\text {solid-tide }}+ \\ V_{\text {ocean-tide }}+V_{\text {atmosphere-tide }}+V_{\text {pole-tide }} \end{gathered} $ | (2) |
双星积分式由单星积分式作差获得:
| $ \begin{gathered} T_{12}-E_{012}=\frac{1}{2}\left(\dot{\boldsymbol{r}}_{1}-\dot{\boldsymbol{r}}_{2}\right)-U_{012}-V_{\text {conv12 }} \\ \omega\left[\left(r_{x} \dot{r}_{y}-r_{y} \dot{r}_{x}\right)_{1}-\left(r_{x} \dot{r}_{y}-r_{y} \dot{r}_{x}\right)_{2}\right]- \\ {\left[\left(\int \dot{\boldsymbol{r}} \boldsymbol{f}_{\text {non }} \mathrm{d} t\right)_{1}-\left(\int \dot{\boldsymbol{r}} \boldsymbol{f}_{\text {non }} \mathrm{d} t\right)_{2}\right]} \end{gathered} $ | (3) |
式中,下标1、2为单星的编号,下标12表示1、2星对应项相减。将扰动位T球谐展开:
| $ \begin{gathered} T=\frac{G M}{r} \sum\limits_{n=2}^{\text {maxDegree }}\left(\frac{R}{r}\right)^{n} \sum\limits_{m=0}^{n}\left(\bar{C}_{{nm }}^{*} \cos m \lambda+\right. \\ \left.\bar{S}_{n m} \sin m \lambda\right) \bar{P}_{n m}(\sin \varphi) \end{gathered} $ | (4) |
式中,(r, φ, λ)为卫星的地心球坐标,maxDegree为模型最大阶数,G为引力常量,M为地球质量,Pnm(sinφ)为完全正常化连带Legendre函数,Cnm*、Snm即为待求位系数。
综合式(1)~(4),顾及球坐标与直角坐标的转换关系,基于单星和双星能量守恒方程可构建统一的观测方程:
| $ \begin{gathered} {\left[\underset{1 \times 2 n}{\boldsymbol{A}(\boldsymbol{r})} \quad 1\right]_{i}\left[\begin{array}{c} \underset{n \times 1}{\overline{\boldsymbol{C}}^{*} }\\ \underset{n \times 1}{\overline{\boldsymbol{S}}} \\ E_{0} \end{array}\right]=} \\ {\left[\boldsymbol{F}(\boldsymbol{r}, \dot{\boldsymbol{r}})-\int \dot{\boldsymbol{r}} \boldsymbol{f}_{\mathrm{non}} \mathrm{d} t\right]_{i}+v_{i}} \end{gathered} $ | (5) |
式中,A(r)为卫星位置r的函数向量,F(r,
并行算法的设计主要围绕两个方面,分别为观测方程的并行计算和法方程的并行计算,下面围绕这两点进行讨论。
2.1 观测方程的并行计算观测方程的并行计算由CUDA实现。CUDA将计算任务划分为如图 1所示格网,每个GPU线程完成对应格网的任务,线程通过索引值index获取对应历元的观测数据,索引值index的计算方式如下:
| $ \begin{gathered} \text { index }=\text { blockIdx. x} * \text { blockDim. x} +\\ \text { threadIdx. x} \end{gathered} $ | (6) |
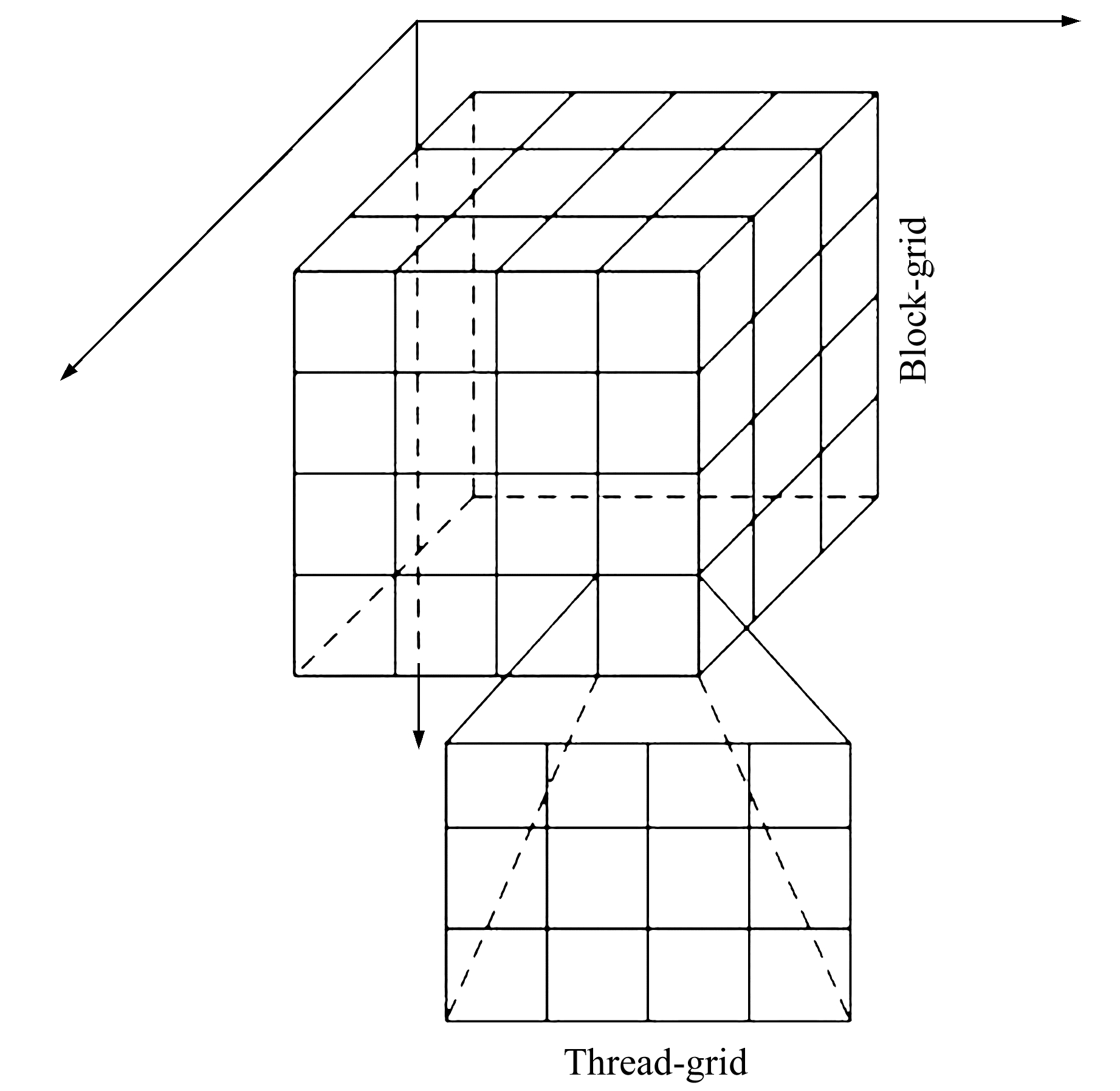
|
图 1 任务格网 Fig. 1 Task-grid |
式中,blockDim为线程块格网的维度,blockIdx为线程块在格网中的编号,threadIdx为线程在线程块中的编号。
GPU可开辟与其核心数同样多的线程。以GTX1080为例,其拥有2 560个核心,可开辟2 560个线程同时进行运算,故GPU可充分利用能量守恒方法设计矩阵各行向量的独立性,实现观测方程构建过程的高度并行化,在单位时间内完成更多的计算。同时,为减少计算过程中的循环次数,参考文献[19],将中间变量向量化:
| $ \begin{gathered} \boldsymbol{\eta}^{\mathrm{T}}=\left[\begin{array}{c} \sin 0 \cdot \lambda \\ \sin 0 \cdot \lambda \\ \sin 1 \cdot \lambda \\ \vdots \\ \left.\begin{array}{c} \sin 0 \cdot \lambda \\ \vdots \\ \sin (N-1) \cdot \lambda \end{array}\right\}N\\ \left.\begin{array}{c} \sin 0 \cdot \lambda \\ \vdots \\ \sin N \cdot \lambda \end{array}\right\}N+1 \end{array}\right], \boldsymbol{\mu}^{\mathrm{T}}=\left[\begin{array}{c} \cos 0 \cdot \lambda \\ \cos 0 \cdot \lambda \\ \cos 1 \cdot \lambda \\ \vdots \\ \left.\begin{array}{c} \cos 0 \cdot \lambda \\ \vdots \\ \cos (N-1) \cdot \lambda \end{array}\right\}N\\ \left.\begin{array}{c} \cos 0 \cdot \lambda \\ \vdots \\ \cos N \cdot \lambda \end{array}\right\}N+1 \end{array}\right],\\ \boldsymbol{\phi}^{\mathrm{T}}=\left[\begin{array}{c} \bar{P}_{00}(\cos \theta) \\ \bar{P}_{10}(\cos \theta) \\ \bar{P}_{11}(\cos \theta) \\ \vdots \\ \bar{P}_{N N-1}(\cos \theta) \\ \bar{P}_{N N}(\cos \theta) \end{array}\right], \boldsymbol{\gamma}^{\mathrm{T}}=\left[\begin{array}{c} 1 / r \\ R / r^{2} \\ R / r^{2} \\ \vdots \\ \left.\begin{array}{c} R^{N-1} / r^{N} \\ \vdots \\ R^{N-1} / r^{N} \end{array}\right\}N \\ \left.\begin{array}{c} R^{N} / r^{N+1} \\ \vdots \\ R^{N} / r^{N+1} \end{array}\right\}N +1 \end{array}\right],\\ \boldsymbol{C}=\left[\begin{array}{ccccc} \bar{C}_{00} & \bar{C}_{10} & \bar{C}_{11} & \cdots & \bar{C}_{N N} \end{array}\right]^{\mathrm{T}}, \\ \boldsymbol{S}=\left[\begin{array}{ccccc} \bar{S}_{00} & \bar{S}_{10} & \bar{S}_{11} & \cdots & \bar{S}_{N N} \end{array}\right]^{\mathrm{T}} \end{gathered} $ | (7) |
进而设计矩阵行向量Ai及自由项元素li,皆可由向量运算获得(其中符号“·”表示向量内积,符号“
| $ \left\{\begin{array}{l} \boldsymbol{A}_{i}=G M[\boldsymbol{\phi} \circ \boldsymbol{\gamma} \circ \boldsymbol{\mu} \quad \boldsymbol{\phi} \circ \boldsymbol{\gamma} \circ \boldsymbol{\eta}]_{i} \\ \boldsymbol{l}_{i}=\frac{1}{2} \dot{\boldsymbol{r}}_{i}^{2}-\omega\left(r_{x} \dot{r}_{y}-r_{y} \dot{r}_{x}\right)_{i}-\left(\int \dot{\boldsymbol{r}} \boldsymbol{f}_{\mathrm{non}} \mathrm{d} t\right)_{i}- \\ \quad (\boldsymbol{\phi} \circ \boldsymbol{\gamma}) \cdot\left(\boldsymbol{\mu} \circ \boldsymbol{C}_{\mathrm{conv}}+\boldsymbol{\eta} \circ \boldsymbol{S}_{\mathrm{conv}}\right)_{i}^{\mathrm{T}} \end{array}\right. $ | (8) |
MKL(math kernel library)库是由Intel提供的函数库,经过了高度优化,并实现了CPU上的并行计算,能提供包括线性代数在内的各类数学运算,具有较高的性能和稳定性。利用MKL库中的cblas_dgemm函数可实现大型矩阵的乘法快速并行运算。
在构建法方程时,传统算法需要将设计矩阵整体记录在内存,当面对海量观测数据时,设计矩阵将占用巨大的内存空间。以卫星182 d数据、60 s采样间隔反演120阶模型为例,此时将获得262 080条数据记录,设计矩阵需28.12 G内存空间进行存储,个人电脑难以提供足够大小的内存。针对大型设计矩阵在
存储时存在内存需求大的问题,可采用分区平差的方法,对观测数据按时序进行分区处理。将观测数据分区后,可得各分区的误差方程:
| $ \left\{\begin{array}{c} \boldsymbol{V}_{1}=\boldsymbol{A}_{1} \boldsymbol{X}+\boldsymbol{B}_{1} \boldsymbol{Y}_{1}+\boldsymbol{L}_{1} \\ \vdots \\ \boldsymbol{V}_{k}=\boldsymbol{A}_{k} \boldsymbol{X}+\boldsymbol{B}_{k} \boldsymbol{Y}_{k}+\boldsymbol{L}_{k} \end{array}\right. $ | (9) |
式中,Ai、Bi和Li分别为i分区的设计矩阵和自由项向量。各分区分别构建法方程,消去区域性未知数Yi,得到仅含联系未知数的约化法方程:
| $ \begin{gathered} \left(\boldsymbol{A}_{i}^{\mathrm{T}} \boldsymbol{A}_{i}-\boldsymbol{A}_{i}^{\mathrm{T}} \boldsymbol{B}_{i}\left(\boldsymbol{B}_{i}^{\mathrm{T}} \boldsymbol{B}_{i}\right)^{-1} \boldsymbol{B}_{i}^{\mathrm{T}} \boldsymbol{A}_{i}\right) \boldsymbol{X}= \\ \boldsymbol{A}_{i}^{\mathrm{T}} \boldsymbol{L}_{i}-\boldsymbol{A}_{i}^{\mathrm{T}} \boldsymbol{B}_{i}\left(\boldsymbol{B}_{i}^{\mathrm{T}} \boldsymbol{B}_{i}\right)^{-1} \boldsymbol{B}_{i}^{\mathrm{T}} \boldsymbol{L}_{i}, i=1, \cdots, k \end{gathered} $ | (10) |
将各联系未知数的约化法方程系数和自由项相加,获得总体约化法方程的法矩阵与自由项:
| $ \left\{\begin{array}{l} \boldsymbol{N}=\sum\limits_{i=1}^{k} \boldsymbol{A}_{i}^{\mathrm{T}} \boldsymbol{A}_{i}-\sum\limits_{i=1}^{k} \boldsymbol{A}_{i}^{\mathrm{T}} \boldsymbol{B}_{i}\left(\boldsymbol{B}_{i}^{\mathrm{T}} \boldsymbol{B}_{i}\right)^{-1} \boldsymbol{B}_{i}^{\mathrm{T}} \boldsymbol{A}_{i} \\ \boldsymbol{U}=\sum\limits_{i=1}^{k} \boldsymbol{A}_{i}^{\mathrm{T}} \boldsymbol{L}_{i}-\sum\limits_{i=1}^{k} \boldsymbol{A}_{i}^{\mathrm{T}} \boldsymbol{B}_{i}\left(\boldsymbol{B}_{i}^{\mathrm{T}} \boldsymbol{B}_{i}\right)^{-1} \boldsymbol{B}_{i}^{\mathrm{T}} \boldsymbol{L}_{i} \end{array}\right. $ | (11) |
解算总体约化法方程便能求得联系未知数X,若需进一步求取区域性未知数,则将X回代至各分区法方程中即可。利用分区平差法,每次计算仅需原有内存需求的ni/n(n为总观测数,ni为各分区观测数)。与MKL库结合后,在减小对硬件资源消耗的同时能够快速完成法矩阵及自由项计算。
在解算法方程时,采用预处理共轭梯度法[17],并引入MKL库并行加速相关线性代数运算,可以兼顾解算精度和计算效率。
3 实验结果与分析 3.1 实验平台与数据准备实验计算平台为戴尔Precision 7530移动工作站,CPU为Intel Xeon(频率为2.9 GHz,6核12线程),内存容量32 GB,GPU为NVIDIA Quadro P3200(6 G显存,1 792个CUDA核心)。程序编译环境为Visual Studio 2015-Visual C++,CUDA10.0,OpenMP2.0并行库与MKL19.0科学计算库。实验所涉及算法都在Debug模式下进行测试。
本文数据来源如下:1)由德国GFZ(German Research Centre for Geosciences) ISDC(Information System and Data Center for Geoscientific Data) 数据中心提供的GRACE-FO卫星1 Hz精密轨道数据GNV1B、加速度计数据ACT1B、卫星姿态数据SCA1B以及0.5 Hz星间激光干涉测距数据LRI1B、0.2 Hz Ka/K波段测距数据KBR1B(测距数据主要用于双星动能差的计算[6, 17]),各类数据都以每天一个文件的形式保存;2)海洋潮汐数据来自于EOT11a模型;3)日月星历数据由DE430模型计算获得。
对于卫星数据,首先利用观测数据标准差依据3σ准则进行粗差剔除;然后用5阶牛顿插值填补跨度小于30 s的缺失历元数据,对于无法内插的历元则用0补足;同时舍弃缺失历元数过半的数据,最终获得166 d的可用数据,每天有86 400个观测历元,总数据量为13.77 GB。
3.2 反演精度分析利用本文算法处理GRACE-FO卫星2020-01-01~06-30共166 d的可用数据,反演获得120阶重力场模型GM-GraceFO2020h。为检验反演精度,将ITU_GRACE16、HUST-Grace2016s、Tongji-Grace02s、GGM05S等GRACE重力场模型作为对比组,与GM-GraceFO2020h进行对比分析。同时选取2 190阶模型EIGEN-6C4(该模型综合了LAGEOS-1/2、GRACE、GOCE以及地形数据,具有较高的精度[20])作为基准,对比检验模型内符合精度。
用GM-GraceFO2020h与4个对比组模型(截断至120阶)分别计算全球1°×1°高程异常与重力异常格网,并求取各自相较于EIGEN-6C4的差值,统计结果如表 1所示。
|
|
表 1 各重力场模型与EIGEN-6C4模型间高程异常、重力异常差值 Tab. 1 Differences between EIGEN-6C4 and other gravity models in height anomaly and gravity anomaly |
由表 1可知,GM-GraceFO2020h与EIGEN-6C4的模型高程异常、重力异常差值相较于对比组,在数值上相近,差值最小值的差异分别在7 cm和1.2 mGal以内,最大值的差异分别在15 cm和11 mGal以内,平均值和标准差的差异分别在0.1 cm、0.001 mGal和0.2 cm、0.003 mGal以内。图 2为GM-GraceFO2020h与对比组模型相较于EIGEN-6C4的阶方差。由图 2可见,GM-GraceFO2020h与GRACE重力场模型在各阶位系数上的差异较小,总体上精度相近。图 3为GM- GraceFO2020h阶方差曲线,其与Kaula曲线基本吻合,说明该模型与Kaula准则符合度较高,具有较高的内符合精度。图 4为该模型的重力异常、纬向垂线偏差和高程异常。
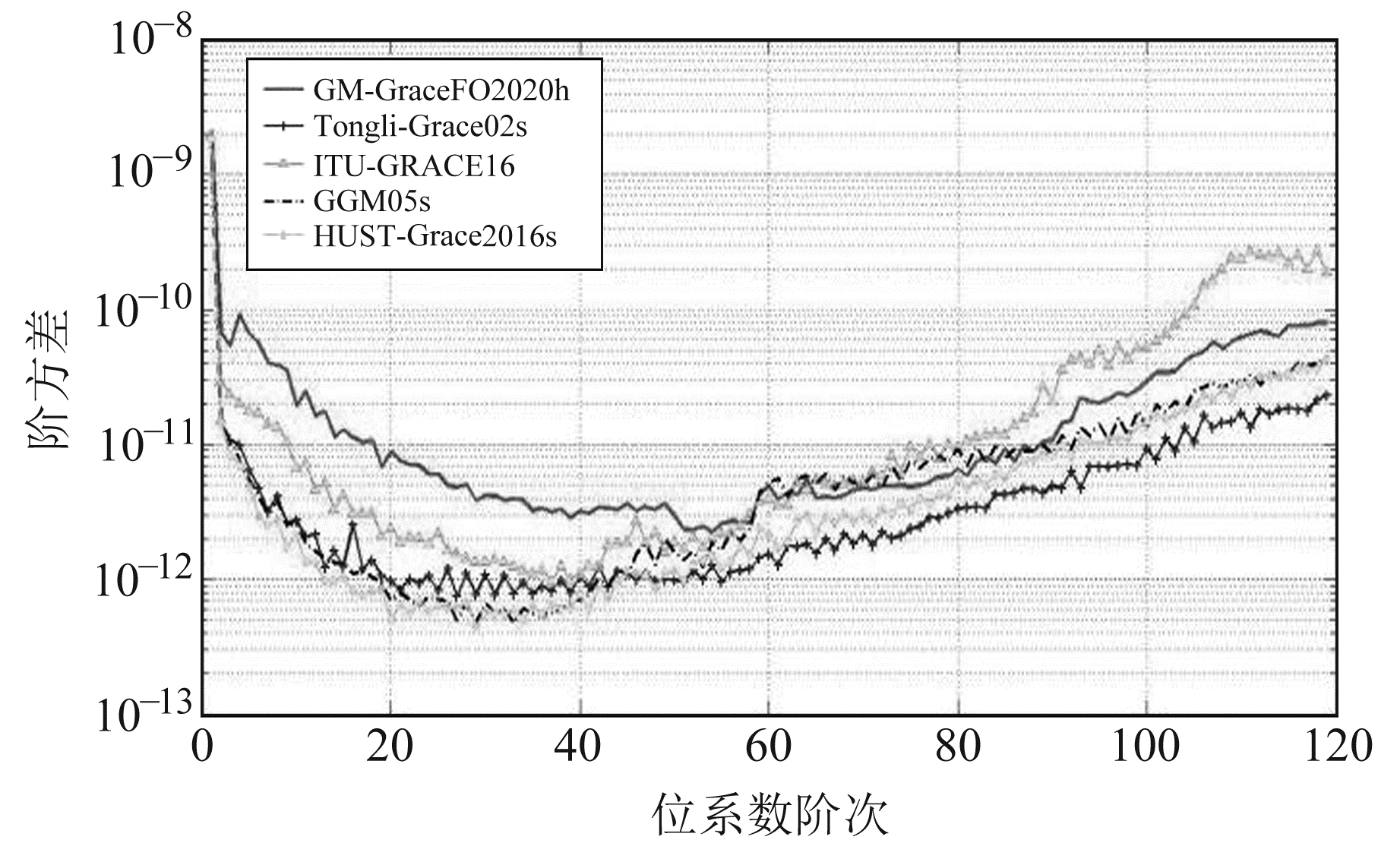
|
图 2 各模型与EIGEN-6C4位系数差的阶方差 Fig. 2 Difference degree with EIGEN-6C4 |
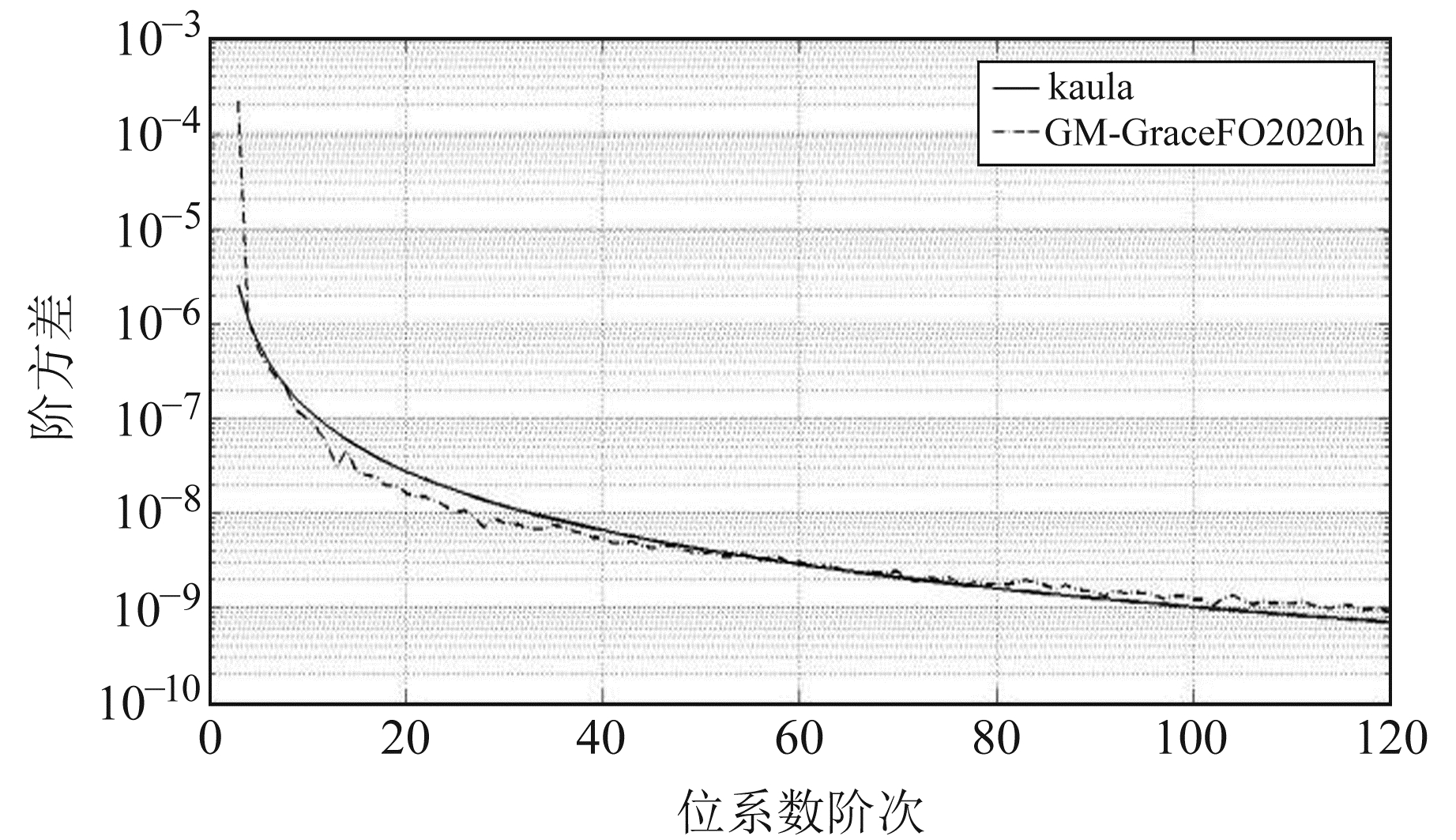
|
图 3 GM-GraceFO2020h模型阶方差 Fig. 3 Degree variance of GM-GraceFO2020h |

|
图 4 GM-GraceFO2020h模型重力异常、纬向垂线偏差、高程异常 Fig. 4 Gravity anomaly, deflection of the vertical and height anomaly derived from GM-GraceFO2020h |
从观测方程构建、法矩阵计算、法方程解算3个方面对快速反演算法的计算效率进行分析。同时,引入并行加速比Sn[21]作为量化加速效果的参数:
| $ S_{n}=\frac{t_{1}}{t_{n}} $ | (12) |
式中,n表示参与运算的线程数,tn表示有n个线程参与时完成运算所需的时间。
3.3.1 观测方程构建在对数据进行60 s间隔采样条件下,分别利用串行算法与快速反演算法完成如下计算任务:1)处理卫星23 d数据(共29 011条记录),构建60阶模型3 716个待求参数的观测方程;2)处理75 d数据(共100 960条记录),构建96阶模型9 404个待求参数的观测方程;3)处理166 d数据(共225 341条记录),构建120阶模型14 636个待求参数的观测方程。表 2为各任务耗时情况。
|
|
表 2 不同数据规模的计算任务耗时对比 Tab. 2 Comparison of computing time of tasks |
对比结果显示,传统串行算法耗时随着计算量的增大呈线性递增趋势;而本文提出的算法在构建观测方法时,相较于串行算法,能有效提高计算效率,其并行加速比达到20以上,但随着计算量的增加,加速比会逐渐减小到10左右。
3.3.2 法矩阵计算分别用串行算法、OpenMP算法[11]、快速反演算法计算956阶(设计矩阵维度为8 862×956)、3 716阶(设计矩阵维度为29 011×3 716)、9 404阶(设计矩阵维度为100 960×9 404)、14 636阶(设计矩阵维度为225 341×14 636)法矩阵,时间消耗情况如表 3,内存空间消耗情况如图 5。
|
|
表 3 不同阶法矩阵计算耗时情况 Tab. 3 Computing time of constructing normal matrix |
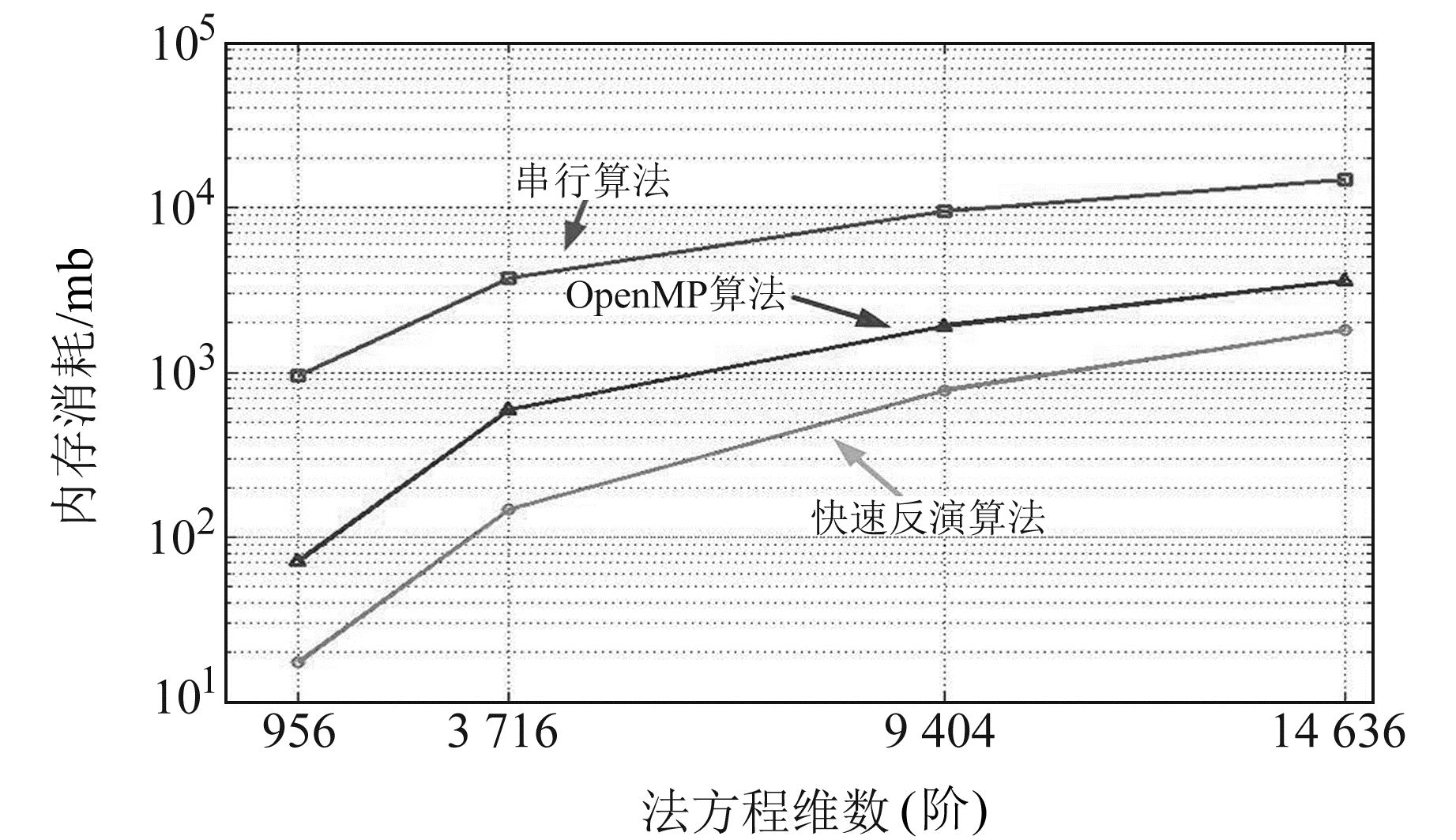
|
图 5 内存空间消耗情况 Fig. 5 Memory consumption |
结合表 3和图 5可见,快速反演算法完成各计算任务所需时间分别是串行算法的7.660%、2.753%、1.763%和1.537%,并行加速比在13~66之间,是OpenMP算法的52.078%、17.756%、11.869%和10.186%,其计算效率优于二者。本文算法的内存消耗是串行算法的1/20,较之小一个量级,也是OpenMP算法的1/2;同时,串行算法的内存消耗会随着法矩阵和设计矩阵维度的增加而快速增大,而本文算法的增速较小。通过以上分析可得,快速反演算法综合MKL库与分区平差法二者优势,相较于现有算法,在快速计算法矩阵的同时有效限制了对内存资源的消耗,大幅降低了模型反演对计算平台硬件水平的要求,使得在内存资源有限的普通PC上处理大规模卫星重力数据成为可能。
3.3.3 法方程解算分别利用串行算法(Gauss-Jordan法)、MKL算法[14](LU分解求逆法)、快速反演算法,求解不同维数的法方程,计算耗时情况如表 4。
|
|
表 4 不同维数法方程解算耗时对比 Tab. 4 Comparison of computing time of solving equations |
由表 4可见,快速反演算法在法矩阵阶数为116时的解算耗时略多于MKL算法0.004 s,其主要原因在于,计算量较小时内存读写耗时具有较大占比;而在其余情况下其耗时皆低于前两种算法,说明该算法将MKL库与预处理共轭梯度法相结合,能有效加快法方程的解算速度。但需要注意,共轭梯度法并不对法矩阵求逆,故需估计所求位系数的精度时,仍推荐使用MKL算法。
3.3.4 反演计算总体情况分别利用串行算法和快速反演算法处理卫星166 d数据,反演120阶重力场模型,计算耗时总体情况如表 5所示。
|
|
表 5 反演计算总体耗时 Tab. 5 Total computing time of gravity recovery |
由表 5可见,串行算法反演耗时超过19 h,而快速反演算法仅需约17 min,反演耗时缩减98.479%,并行加速比超过65。算法耗时最多的计算过程为法方程的构建,可采用仅计算法矩阵下三角部分、引入斯特拉森(Strassen)算法等方式来进一步优化算法,提高计算效率。
4 结语本文基于能量守恒方法,提出重力场反演快速异构并行算法。该算法实现了GPU并行计算设计矩阵与自由项向量,通过结合MKL库与分区平差、预处理共轭梯度法来快速构建并解算法方程。利用本文算法处理GRACE-FO卫星2020-01-01~06-30期间数据,反演获得120阶重力场模型GM-GraceFO2020h。通过对比实验,分析验证了算法的反演精度与计算效率。
在反演精度方面,快速反演算法所得模型与现有GRACE重力场模型在前120阶精度相当,具有较高的内符合精度。在计算效率方面,该算法在重力场反演各主要计算过程的计算效率都优于现有算法,相较于传统串行算法,反演耗时缩减98.479%,内存消耗减小1个量级。综上所述,本文提出的重力场反演快速异构并行算法,能在保证反演精度的同时,有效提高计算效率,减少反演耗时,降低硬件需求,可以为大规模处理卫星重力数据提供经济高效的计算实施方案。
致谢: 感谢德国GFZ ISDC数据中心提供GRACE-FO卫星轨道、姿态、激光干涉测距及加速度计数据。
| [1] |
陈秋杰, 沈云中, 张兴福, 等. 基于GRACE卫星数据的高精度全球静态重力场模型[J]. 测绘学报, 2016, 45(4): 396-403 (Chen Qiujie, Shen Yunzhong, Zhang Xingfu, et al. GRACE Data-Based High Accuracy Global Static Earth's Gravity Field Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 396-403)
(  0) 0) |
| [2] |
张传定, 吴晓平. 卫星重力空域调和分析方法与技术指标可行性分析[C]. 中国地球物理学会第十九届年会, 南京, 2003 (Zhang Chuanding, Wu Xiaoping. Feasibility Analysis of Satellite Gravity Space Domain Harmonic Analysis Method and Technical Index[C]. 19th Annual Meeting of Chinese Geophysical Society, Nanjing, 2003)
(  0) 0) |
| [3] |
王正涛, 李建成, 姜卫平, 等. 基于GRACE卫星重力数据确定地球重力场模型WHU-GM-05[J]. 地球物理学报, 2008, 51(5): 1364-1371 (Wang Zhengtao, Li Jiancheng, Jiang Weiping, et al. Determination of Earth Gravity Field Model WHU-GM-05 Using GRACE Gravity Data[J]. Chinese Journal of Geophysics, 2008, 51(5): 1364-1371 DOI:10.3321/j.issn:0001-5733.2008.05.010)
(  0) 0) |
| [4] |
徐天河, 杨元喜. 基于能量守恒方法恢复CHAMP重力场模型[J]. 测绘学报, 2005, 34(1): 1-6 (Xu Tianhe, Yang Yuanxi. CHAMP Gravity Field Recovery Using Energy Conservation Method[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(1): 1-6 DOI:10.3321/j.issn:1001-1595.2005.01.001)
(  0) 0) |
| [5] |
Jekeli C. The Determination of Gravitational Potential Differences from Satellite-to-Satellite Tracking[J]. Celestial Mechanics and Dynamical Astronomy, 1999, 75(2): 85-101 DOI:10.1023/A:1008313405488
(  0) 0) |
| [6] |
冉将军, 许厚泽, 钟敏, 等. 利用GRACE重力卫星观测数据反演全球时变地球重力场模型[J]. 地球物理学报, 2014, 57(4): 1032-1040 (Ran Jiangjun, Xu Houze, Zhong Min, et al. Global Temporal Gravity Field Recovery Using GRACE Data[J]. Chinese Journal of Geophysics, 2014, 57(4): 1032-1040)
(  0) 0) |
| [7] |
苏勇, 范东明, 游为. 利用GOCE卫星数据确定全球重力场模型[J]. 物理学报, 2014, 63(9): 448-456 (Su Yong, Fan Dongming, You Wei. Gravity Field Model Calculated by Using the GOCE Data[J]. Acta Physica Sinica, 2014, 63(9): 448-456)
(  0) 0) |
| [8] |
苏勇, 范东明. 利用短弧积分法和GOCE轨道数据确定地球重力场模型[J]. 地球物理学进展, 2014, 29(5): 2072-2076 (Su Yong, Fan Dongming. Gravity Field Modeling by Using the Short-Arc Integral Approach and GOCE Orbits[J]. Progress in Geophysics, 2014, 29(5): 2072-2076)
(  0) 0) |
| [9] |
张兴福, 沈云中. 联合GRACE卫星轨道及距离变率数据反演地球重力场方法研究[J]. 大地测量与地球动力学, 2011, 31(2): 66-70 (Zhang Xingfu, Shen Yunzhong. Method of Gravity Field Inversion with Combining GRACE Orbits and Range-Rate Observations[J]. Journal of Geodesy and Geodynamics, 2011, 31(2): 66-70)
(  0) 0) |
| [10] |
邹贤才, 李建成, 汪海洪, 等. OpenMP并行计算在卫星重力数据处理中的应用[J]. 测绘学报, 2010, 39(6): 636-641 (Zou Xiancai, Li Jiancheng, Wang Haihong, et al. Application of Parallel Computing with OpenMP in Data Processing for Satellite Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 636-641)
(  0) 0) |
| [11] |
周浩, 钟波, 罗志才, 等. OpenMP并行算法在卫星重力场模型反演中的应用[J]. 大地测量与地球动力学, 2011, 31(5): 123-127 (Zhou Hao, Zhong Bo, Luo Zhicai, et al. Application of Parallel Algorithms Based on OpenMP to Satellite Gravity Field Recovery[J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 123-127)
(  0) 0) |
| [12] |
周浩, 罗志才, 钟波. 大规模矩阵的MPI并行求逆算法设计与分析[J]. 大地测量与地球动力学, 2014, 34(5): 120-124 (Zhou Hao, Luo Zhicai, Zhong Bo. Design and Analysis of MPI Parallel Algorithm for Large-Scale Matrix Inversion[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 120-124)
(  0) 0) |
| [13] |
周浩, 罗志才, 钟波, 等. 利用最小二乘直接法反演卫星重力场模型的MPI并行算法[J]. 测绘学报, 2015, 44(8): 833-839 (Zhou Hao, Luo Zhicai, Zhong Bo, et al. MPI Parallel Algorithm in Satellite Gravity Field Model Inversion on the Basis of Least Square Method[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 833-839)
(  0) 0) |
| [14] |
陈秋杰, 沈云中, 张兴福. MKL和OpenMP多核并行算法解算高阶地球重力场的效率分析[J]. 大地测量与地球动力学, 2012, 32(5): 118-123 (Chen Qiujie, Shen Yunzhong, Zhang Xingfu. Analysis of Efficiency of Applying MKL and OpenMP Polynuclear Parallel Algorithms to Recovery of High Degree Earth's Gravity Field[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 118-123)
(  0) 0) |
| [15] |
聂琳娟, 申文斌, 王正涛, 等. 基于超级计算机平台的并行解算技术在卫星重力测量中的应用[J]. 大地测量与地球动力学, 2012, 32(2): 64-68 (Nie Linjuan, Shen Wenbin, Wang Zhengtao, et al. Applications of Parallel Solutions Technology in Satellite Gravity Measurement[J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 64-68)
(  0) 0) |
| [16] |
黄维彬. 近代平差理论及其应用[M]. 北京: 解放军出版社, 1992 (Huang Weibin. Modern Adjustment Theory and Its Application[M]. Beijing: PLA Publishing House, 1992)
(  0) 0) |
| [17] |
郑伟. 基于能量守恒原理的卫星重力反演理论与方法[M]. 北京: 科学出版社, 2015 (Zheng Wei. Theory and Method of Satellite Gravity Inversion Based on Energy Conservation Principle[M]. Beijing: Science Press, 2015)
(  0) 0) |
| [18] |
王正涛. 卫星跟踪卫星测量确定地球重力场的理论与方法[D]. 武汉: 武汉大学, 2005 (Theory and Methodology of Earth Gravity Field Recovery by Satellite-to-Satellite Tracking Data[D]. Wuhan: Wuhan University, 2005)
(  0) 0) |
| [19] |
周蓓, 黄永忠, 许瑾晨, 等. 向量数学库的向量化方法研究[J]. 计算机科学, 2019, 46(1): 320-324 (Zhou Bei, Huang Yongzhong, Xu Jinchen, et al. Study on SIMD Method of Vector Math Library[J]. Computer Science, 2019, 46(1): 320-324)
(  0) 0) |
| [20] |
Kostelecký J, Klokoǒník J, Bucha B, et al. Evaluation of Gravity Field Model EIGEN-6C4 by Means of Various Functions of Gravity Potential, and by GNSS/Leveling[J]. Geoinformatics FCE CTU, 2015, 14(1): 7-28 DOI:10.14311/gi.14.1.1
(  0) 0) |
| [21] |
吴建平, 王正华, 李晓梅. 利用混合编程改善SMP机群上并行矩阵乘法的性能[J]. 国防科技大学学报, 2006, 28(4): 68-72 (Wu Jianping, Wang Zhenghua, Li Xiaomei. Improve the Performance of Parallel Matrix Multiplication on Clustered SMP Systems through Hybrid Programming[J]. Journal of National University of Defense Technology, 2006, 28(4): 68-72 DOI:10.3969/j.issn.1001-2486.2006.04.015)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


