精密水准是用于测量地表点位高程的传统大地测量手段之一[1-2];GNSS测量则是近30 a来迅速发展起来的新技术,能快速给出地面点的三维坐标。研究表明,对于同一个点,二者给出的垂向坐标存在差异,但属于近似不变的系统性差异,其对点位垂向变化量计算的影响可以忽略。因此,通过分析不同时段观测结果的变化,二者都能较好地给出地表点的垂直形变量[3]。但实践中发现,不同来源的资料、不同技术手段得到的资料、相同资料用不同处理方法给出的结果往往不同,有时差异很大,甚至完全相反。对比以精密水准给出的全国垂直形变矢量图和GNSS给出的垂直形变矢量图发现,两者在天山构造带及塔里木盆地区域差异最大,在天山构造带甚至完全相反。本文针对这一差异进行分析与研究,探讨其中可能存在的问题,分析形成差异的原因。
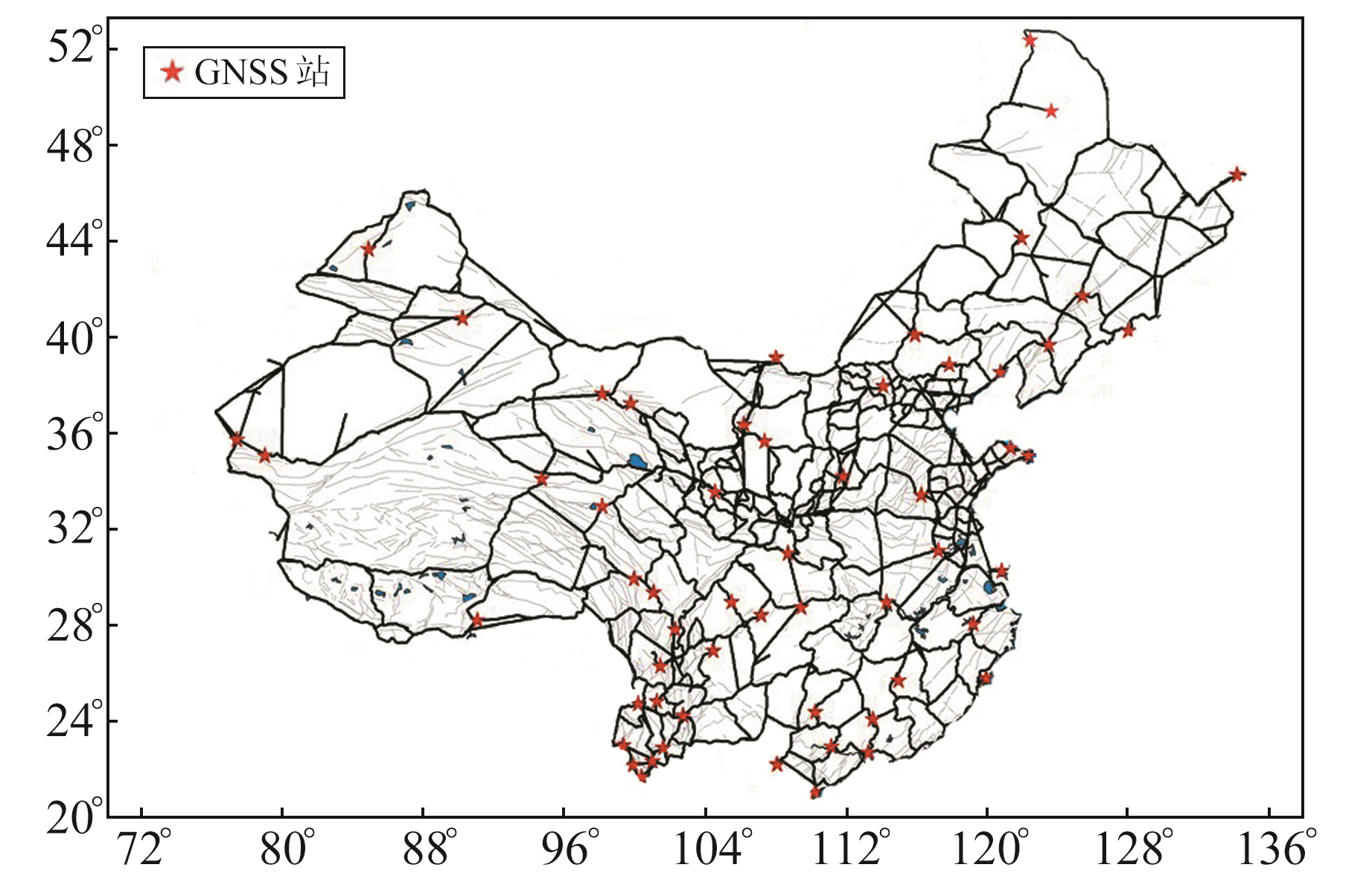
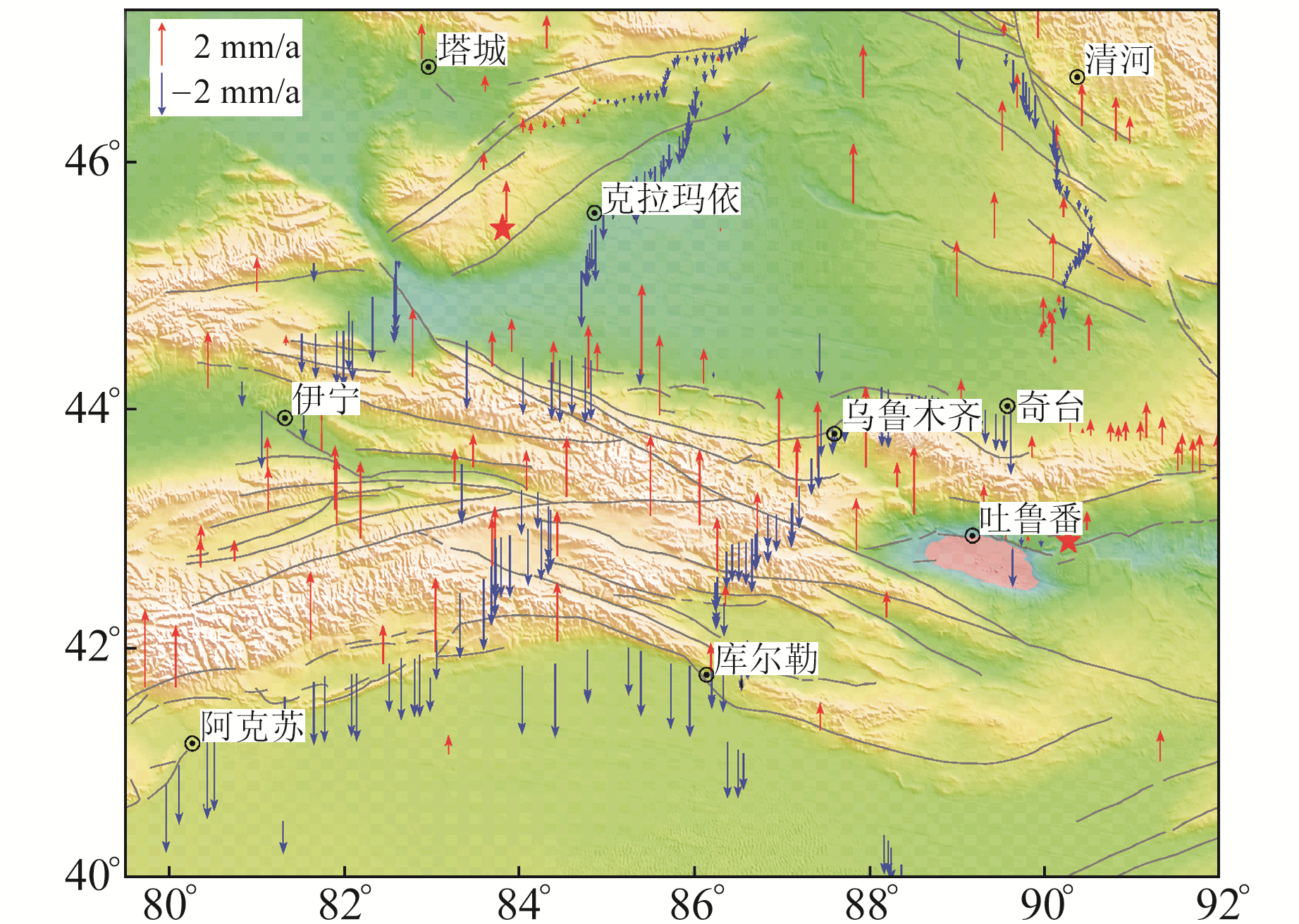
1 以精密水准为主给出的垂直形变矢量图图 1是以精密水准给出的天山构造带及塔里木盆地区域垂直形变矢量图(割圆锥投影)。所用资料为2期全国精密水准资料,第1期中心时刻为1980年,第2期中心时刻为2010年,获得该期间全国垂直形变图后,截取天山构造带区域部分,即为图 1。为了抑制精密水准随路线长度增加而导致的误差累积的影响,优选全国57个GNSS连续站垂向运动速率作为约束(均为与水准点有2期以上联测成果的GNSS连续站,其分布见图 2),利用赫尔默特平差方法[4]得到各个水准点的垂向运动速率。全部GNSS站点坐标运动速率是在全球GNSS参考框架下统一解算的,用57个GNSS连续站的垂向速率对全国水准网的速率平差进行约束,因GNSS站的垂向速率统计精度相对均匀且高于考虑误差传播和累积后由单一水准测量得到的垂向运动速率的精度,约束的结果相当于统一了精密水准与GNSS的垂向速率基准。当然这只有在地壳垂向速率为线性的前提下才是严密的,实际上地壳垂直运动速率的变化是非线性的,水准与GNSS资料覆盖的时段又不完全吻合,因此二者速率基准的统一是相对的和近似的,尚存在一定的误差。

|
图 1 以精密水准为主给出的天山构造带及塔里木盆地区域垂直形变速率矢量图(1980~2010年) Fig. 1 Vector diagram of vertical deformation rate in Tianshan tectonic belt and Tarim basin mainly based on precision leveling (1980-2010) |
|
图 2 精密水准路线及2期57个联测GNSS连续站分布示意图 Fig. 2 Schematic diagram of precision leveling routes and57GNSS stations with2times of joint measurement |
以精密水准为主给出的垂直形变图显示,该区域的水准点总体上以相对沉降运动为主。
由图 2可见,西部符合条件的GNSS联测点较少,本文研究范围内(天山构造带附近)只有2个点,扩大到塔里木盆地有4个点,这4个联测点的情况见表 1。
|
|
表 1 天山构造带及塔里木盆地区域4个GNSS联测点的相关参数 Tab. 1 Parameters of4joint measuring points of GNSS in Tianshan tectonic belt and Tarim basin |
对比表 1和图 1可见,XJHT、XJSS、XJYC站的垂向速率都对附近的水准速率起到了很好的约束作用;而XJKL站的GNSS垂向速率为7.0 mm/a,在图 1中似乎对附近的水准速率失去了约束作用,经核查发现,该站的垂向运动速率确实高。7.0 mm/a的运动速率是真实的,水准联测数据也恰好证明了这一点。大面积形变重点研究空间上相对低频的垂直形变信息,在GNSS垂向形变图中通过统一的判别标准将XJKL点作为奇异点进行剔除,因此在后面的GNSS形变图中未体现该点突出的垂直运动。但该点恰好有2期与水准联测的成果,资料完整,考虑该区域缺少符合条件的联测点,故在联合平差中仍将其作为联测点使用,同样起到了很好地约束于统一速率基准的作用。
2 GNSS给出的垂直形变速率矢量图GNSS垂向分量精度较低,但与精密水准相比,不存在长距离误差累积和传递的问题,各GNSS点之间具有一定的相对独立性,当GNSS资料足够丰富时,给出的垂向形变信息具有一定的可信性。中国大陆近20 a来积累了比较丰富的GNSS资料,笔者尝试用GNSS资料给出一张中国大陆GNSS垂直形变速率矢量图,截取其中天山构造带及塔里木盆地区域得到图 3。

|
图 3 GNSS给出的天山构造带及塔里木盆地区域垂直形变速率矢量图(1999~2018年) Fig. 3 Vector diagram of vertical deformation rate in Tianshan tectonic belt and Tarim basin based on GNSS (1999-2018) |
对比图 1和图 3可以看出,精密水准给出的垂向形变几乎是整体沉降,GNSS给出的垂向形变几乎是整体抬升,即使所跨时段稍有不同,也不应该有如此明显的差异。
首先考虑两者测点空间分布差异的影响。GNSS测点要求尽量选在稳定的地方,且希望能同时收到尽可能多的卫星信号,一般要远离断层、河流、低洼等不稳定和卫星高度角不满足要求的地方,因此,GNSS观测站点多选在山头等视线开阔、海拔相对较高的地方;而水准路线的布设则要重点考虑便于观测的问题,往往沿道路两边选点,尤其在山区,遇到高山能绕开必须绕开,往往要从高山之间的峡谷穿过。这就使GNSS和水准的重合点非常少,仅有少量几个经过联测并用于平差约束的GNSS连续站可作为二者的重合点。但就是这少量重合点,也可将二者的垂直形变速率基准统一起来,不应该有如此大的差异。
将二者的矢量合在一起,直接绘到同一张图上(图 4,墨卡托投影, 单位mm/a)则可以看出,二者虽然总体上升降相互矛盾,但具体的点位分布却相互错开。正如前文所述,水准点多为沉降,处于相对低的位置;GNSS点多为隆升,处于相对高的位置。高低之差形成的原因主要是垂向构造活动存在差异所致,因此正常情况下点位垂直运动速率存在差异也在情理之中。仔细分析可见,图 4中仍有少量相互矛盾的地方,考虑到观测误差、图 1和图 3观测数据所跨时段的差异以及地壳构造活动在空间的非均匀性和时间上的非线性等多因素影响,存在少量相互矛盾的地方是可以理解的。
|
图 4 天山构造区垂直形变速率矢量图(图 1和图 3资料合并绘制,墨氏投影) Fig. 4 Vector diagram of vertical deformation rate in Tianshan tectonic region(combined drawing of data in Fig. 1 and Fig. 3, Mercator projection) |
利用图 4数据,采用克里金插值算法绘制等值线图(见图 5,单位mm/a)。图 5显示,虚线勾画出的沉降区恰好为海拔相对低的区域,实线勾画出的隆起区多为山区,与构造地貌吻合较好,在一定程度上较好地反映了该区域在该时段垂向构造活动的空间差异。

|
图 5 天山构造区垂直形变速率等值线图 Fig. 5 Contour map of vertical deformation rate in Tianshan tectonic region (combined drawing of data in Fig. 1 and Fig. 3, Mercator projection) |
图 5给出的结果是用纯数学方法通过空间内插得到的等值线。目前常用的通过内插数据绘制等值线的方法有多种,如最小二乘配置方法[2, 5]、面函数法[6]等。不同方法给出的等值线分布具有很大差异。分析认为,不同的方法和模型各有利弊,所用的数学模型不同,实际上对应着不同的物理意义,有的偏向于低频形变信息,会滤掉很多高频形变成分;有的偏向中高频信息,则掩盖了低频形变信息的变化。因此需要根据实际情况选择相对匹配的方法或方法组合,以得到更为理想的结果。对于图 4分布的垂向矢量,有的两点间距离很近,但高差相差很大,垂向速率相反;有的两点间距离较远,实际上垂向速率陡变的地方大多在盆岭地形的陡变带上,而陡变带难以布设测量点进行控制,靠纯数学的方法内插很难给出理想的拟合结果。基于上述考虑,针对图 4的速率矢量数据进行进一步的融合计算,再给出垂直形变等值线。具体方案如下:
1) 盆岭之间垂直形变零值线的确定。根据点位已有速率分布和构造地形分布,首先确定盆岭构造间垂直形变速率的陡变带。因地形差异就是长期垂向构造运动差异造成的,而水准覆盖时间都在10 a以上,这样确定的垂直形变陡变带比计算机在不考虑构造地形的情况下均匀内插的结果更合理、更接近实际情况。零值线就从陡变带的中间穿过,将该零值线作为约束再绘制等值线图,就会得到更接近实际情况的形变等值线图。
2) 在零值线的约束下,分别用最小二乘配置和多核面函数方法内插拟合图 4的速度矢量数据。
3) 最小二乘配置方法有利于提取低频形变信息,特殊地形造成点位空间密度差异较大时其削峰填谷作用较强,容易失真;多面函数利用核点作控制,利于拟合陡变带的高频形变信息。为使二者互补,基于多核函数给出经典平差分量(用于替代最小二乘配置中经典平差部分)建立最小二乘配置的误差方程,再利用赫尔默特迭代方法确定水准和GNSS两类资料的最佳权重,得到最佳的带权平均结果作为最后的融合计算结果。
4) 利用融合计算结果绘制垂直形变等值线图(图 6,单位mm/a)。由图可见,最终融合结果的垂直形变速率等值线图与实际地形构造分布的吻合度较高,较好地反映了该区域地壳垂向的继承性构造活动。

|
图 6 天山构造区垂直形变速率等值线图(最终融合的结果,墨氏投影) Fig. 6 Vertical deformation rate isoline map of the Tianshan tectonic region (final fusion results, Mercator projection) |
因篇幅限制,本文就几个问题进行初步的讨论。
1) GNSS与水准垂向速率的差异。GNSS和精密水准给出的高程值一个是法线上的高程,一个是垂线上的高程,二者的差异包括大地水准面差距和垂线偏差对高程的影响。理论研究表明,大地水准面差距虽未知,但对于同一个点在相当长的时间内可近似认为是一个常数,其对点位垂向运动速率计算的影响可以忽略;垂线偏差通常是一个很小的角度,对垂向高程变化速率的影响也很微小[3],可以忽略不计。
实际观测和计算研究发现,在同一区域GNSS和水准得到的垂向速率差异有时是比较大的。这一差异是多种因素的综合影响,至于哪一个结果更可靠,还要具体问题具体分析。GNSS垂向坐标测量精度远低于水平向坐标的测量精度,其中气象要素中的周期性干扰影响比较显著,但多年观测的平均垂向运动速率可较好地消除周期性干扰的影响;精密水准的近距离两点高差测量精度较高,对计算垂向形变速率在空间上的变化梯度有较好的控制作用,但高程和垂向运动速率观测和计算结果中的误差则会随着水准路线长度的增加而累积传播。因此,对地壳垂直形变研究来说,二者各有千秋,综合利用,进行融合计算,可达到有益互补的作用。
2) 同区域、同类资料获得的空间形变场的差异。在同一区域,不同的学者使用同一类资料和相同的数据处理方法,也会得到不同的形变场图像,让人感到困惑。这个问题的根源是,资料类别虽然相同,但资料来源可能不同;甚至资料来源相同,但经过预处理和筛选,最后采用的资料并不完全一样。
3) 相同资料不同数据处理方法获得的形变场的差异。有时发现,所用资料完全一样,但不同学者给出的形变场也存在一定的差异,进一步比对发现,常与所用的数据处理方法、绘制形变场图的软件或采用的相关参数不同有关。比如测量平差的方法、程序、参数,数据内插的方法、模型、软件和参数等,每个环节有变化,最后得到的形变场图都会存在一定的差异,有时差异还比较显著。
4) 地壳形变在地震预报中的意义。从前面的讨论得知,不同的资料得到的形变场图肯定不同;而资料相同,用不同方法、程序或参数得到的形变场图像也会不同,因此,不同学者给出的形变场研究结果往往存在一定的差异。这会给用形变图进行地震预测研究带来困惑,尤其是相关专业的研究人员在引用形变研究结果时,往往感到无所适从。
地壳结构十分复杂,地壳应力场发生变化时,因地壳介质各向异性,又被很多尚未认识到的断层切割,地壳形变的响应也必然十分复杂。从频谱分析的角度讲,地壳形变信息的频谱成分十分丰富,不同测点的观测资料包含的空间信息成分不同;不同观测周期的资料包含的时间频谱成分不同;不同的数据处理方法(各种平差、拟合、融合计算等),其数学模型在某种程度上都能起到滤波的作用,对不同频谱的形变信息有不同的选择或抑制作用,有的侧重于低频长周期时空形变信息,有的侧重于中频信息,也有些侧重于高频信息,所以处理结果都不相同。哪一种数据处理方案最好,难以给出定论,因为不同构造环境下孕育不同地震的形变异常信息在时间和空间上的频谱成分不可能一样。
因为测量点位的时空分布不一样,所以研究者用不同资料、不同方法给出的地震形变异常图像会存在差异,这是必然的结果。但基于同一空间分布的同一种资料,用同一套数据处理方法,在同一地区给出长时间的地形变研究的系列成果,往往会发现与地震对应的异常变化,这对研究地震形变前兆具有十分重要的意义。根据多年的研究经验,类似本文给出的形变图对中长期形变异常信息有比较好的体现,在几年到几十年的强震中长期预测研究中可起到较为重要的作用[7-14]。
| [1] |
董鸿闻, 顾旦生, 李国智, 等. 中国大陆现今地壳垂直运动研究[J]. 测绘学报, 2002, 31(2): 100-103 (Dong Hongwen, Gu Dansheng, Li Guozhi, et al. Research on Vertical Recent Crustal Movement of the Chinese Mainland[J]. Acta Geodaetica et Cartographic Sinica, 2002, 31(2): 100-103 DOI:10.3321/j.issn:1001-1595.2002.02.002)
(  0) 0) |
| [2] |
郭春喜, 聂建亮, 王斌, 等. 利用自适应最小二乘配置的GPS水准与重力似大地水准面的拟合[J]. 武汉大学学报: 信息科学版, 2013, 38(1): 44-47 (Guo Chunxi, Nie Jianliang, Wang Bin, et al. The Fitting of GPS-Level and Gravity Quasigeoid Based on Adaptive Collocation[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1): 44-47)
(  0) 0) |
| [3] |
黄立人, 韩月萍, 高艳龙, 等. GNSS连续站坐标的高程分量时间序列在地壳垂直运动研究中应用的若干问题[J]. 大地测量与地球动力学, 2012, 32(4): 10-14 (Huang Liren, Han Yueping, Gao Yanlong, et al. Several Issues in Application of Elevation Component Time Series of GNSS CORS in Vertical Crustal Movement Studying[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 10-14)
(  0) 0) |
| [4] |
Xu P L, Liu J N. Variance Components in Errors-in-Variables Models: Estimability, Stability and Bias Analysis[J]. Journal of Geodesy, 2014, 88(8): 719-734 DOI:10.1007/s00190-014-0717-9
(  0) 0) |
| [5] |
江在森, 刘经南. 应用最小二乘配置建立地壳运动速度场与应变场的方法[J]. 地球物理学报, 2010, 53(5): 1 109-1 117 (Jiang Zaisen, Liu Jingnan. The Method in Establishing Strain Field and Velocity Field of Crustal Movement Using Least Squares Collocation[J]. Chinese Journal of Geophysics, 2010, 53(5): 1 109-1 117)
(  0) 0) |
| [6] |
杨国华, 黄立人. 速率面拟合法中多面函数几个特性的初步数值研究[J]. 地壳形变与地震, 1990, 10(4): 70-82 (Yang Guohua, Huang Liren. Primary Numerical Study of Several Characteristics about Multi-Surface Function in Fitting Method of Velocity Surface[J]. Crustal Deformation and Earthquake, 1990, 10(4): 70-82)
(  0) 0) |
| [7] |
薄万举, 杨国华, 郭良迁, 等. 地壳形变与地震预测研究[M]. 北京: 地震出版社, 2001 (Bo Wanju, Yang Guohua, Guo Liangqian, et al. Research on Crustal Deformation and Earthquake Prediction[M]. Beijing: Seismological Press, 2001)
(  0) 0) |
| [8] |
薄万举, 章思亚, 刘宗坚, 等. 大地形变资料用于地震预测的回顾与思考[J]. 地震, 2007, 27(4): 68-76 (Bo Wanju, Zhang Siya, Liu Zongjian, et al. Review and Thinking about the Application of Geodetic Data to Earthquake Prediction[J]. Earthquake, 2007, 27(4): 68-76)
(  0) 0) |
| [9] |
薄万举. 用流动点资料进行地震中短期预报的方法和尝试[J]. 地壳形变与地震, 1988, 8(4): 359-369 (Bo Wanju. The Method and Trial of Mid-Short-Range Forecast of Earthquake by Use of the Geodetic Data at Sites[J]. Crustal Deformation and Earthquake, 1988, 8(4): 359-369)
(  0) 0) |
| [10] |
薄万举. 用非线性动力学的观点分析形变异常与干扰初探[J]. 地壳形变与地震, 1992, 12(4): 44-48 (Bo Wanju. Preliminary Study for Abnormal Deformation by the Viewpoint of Nonlinear Dynamics[J]. Crustal Deformation and Earthquake, 1992, 12(4): 44-48)
(  0) 0) |
| [11] |
薄万举. 昆仑山口大地震与地形变异常的讨论[J]. 大地测量与地球动力学, 2003, 23(1): 22-28 (Bo Wanju. Discussion of Kunlun Mountain Large Earthquake and Related Anomalies of Crustal Deformation[J]. Journal of Geodesy and Geodynamics, 2003, 23(1): 22-28)
(  0) 0) |
| [12] |
薄万举. 中国大陆地壳形变及孕震机制研究[J]. 山西地震, 2003(3): 37-45 (Bo Wanju. A Study on Crustal Deformation of Continent of China and Mechanism Seismogenic Process[J]. Earthquake Research in Shanxi, 2003(3): 37-45 DOI:10.3969/j.issn.1000-6265.2003.03.015)
(  0) 0) |
| [13] |
薄万举. 形变异常与干扰关系的再认识[J]. 大地测量与地球动力学, 2010, 30(1): 5-8 (Bo Wanju. Study on Relation between Crust Deformation Anomaly and Disturbances[J]. Journal of Geodesy and Geodynamics, 2010, 30(1): 5-8)
(  0) 0) |
| [14] |
薄万举, 郭良迁. "坝体决口"孕震模式[J]. 地壳形变与地震, 2001, 21(4): 103-109 (Bo Wanju, Guo Liangqian. ASeismogenic Pattern Like "Dam Bursting"[J]. Crustal Deformation and Earthquke, 2001, 21(4): 103-109 DOI:10.3969/j.issn.1671-5942.2001.04.014)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

