2. 福州大学土木工程学院,福州市学园路2号,350116
2018-11-26 07:57:24台湾海峡发生6.2级强震,中国地震台网中心发布的震源深度为22 km,台湾省气象局发布的震源深度为12.3 km, 福建台网的编目结果为8 km。准确测定地震震源深度不但对认识震源过程、断层构造、壳幔结构、应力作用、板块运动等一系列问题有重要作用,也对区域内地震活动性研究和地震危害的评价具有重要意义[1-2]。因此,有必要重新精确测定台湾海峡M6.2主震的震源深度。本文使用sPn震相计算震源深度。
1 sPn震相特征和走时方程 1.1 震相特征sPn震相是一种反射转换波,指从震源发出的S波入射地表,其中SV成分会发生反射并转换成P波后入射到莫霍面。当入射角为临界角时,形成Pn波,此时的Pn波是由S波转换而来的,所以记为sPn波。sPn波的观测范围一般在250~1 000 km,是测定近距离浅源地震震源深度值比较实用的震相[3],其振幅通常比Pn波强。虽然其动力学特征保持横波性质(即振幅和周期均大于纵波Pn),但最终以纵波形式出现在地震记录上,所以垂直分量显示比较清晰。若初动清晰可见,波形记录到的sPn波和Pn波反向,sPn波周期一般比Pn波长,出现在Pn和Pg震相之间。
sPn震相识别率取决于信噪比,如果记录信噪比较高,那么sPn震相识别率也高。但sPn震相易受噪音和尾波影响,单台识别可靠性不高;其次,sPn震相较其他近震深度震相(如sPg、sPmP震相等)特征要弱[4-5], 受地壳结构复杂等因素影响较难准确识别,而且地壳的横向不均匀性使得不同方位的台站接收到的sPn与Pn震相的走时差存在些许差别[5]。即便是将多台Pn波对齐后再人工进行sPn震相测定,也会因为sPn与Pn同属首波性质,初动振幅较微弱,到时位置模糊,无法避免人为拾取震相的误差。因此波形互相关技术成为识别sPn震相较为优选的方法。
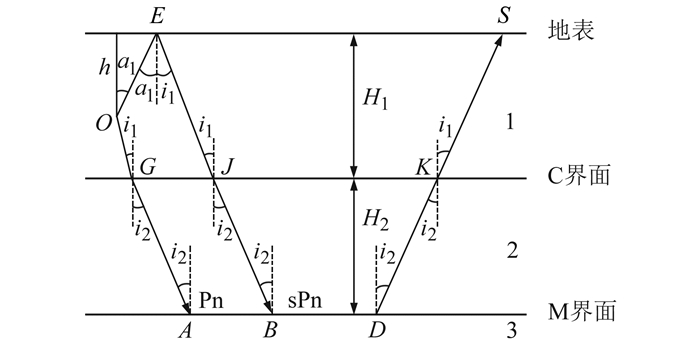
1.2 走时方程本文简单地从双层模型来考虑。首先当震源位于上地壳时(图 1,图中O点表示震源),用v1和v2分别表示P波在上地壳和下地壳内的传播速度,v3表示上地幔顶部P波的传播速度,用vS1和vS2分别表示S波在上地壳和下地壳内的传播速度,h表示震源深度,H1和H2分别表示上下地壳的厚度:
| $ \Delta t=h\left[\frac{\sqrt{v_{3}^{2}-v_{\mathrm{S}_{1}}^{2}}}{v_{3} \cdot v_{\mathrm{S}_{1}}}+\frac{\sqrt{v_{3}^{2}-v_{1}^{2}}}{v_{3} \cdot v_{1}}\right] $ | (1) |
|
图 1 双层模型sPn传播路径(震源在上地壳) Fig. 1 The porpagation path of sPn in double-layer model(epicenter in upper crust) |
式中, Δt为sPn震相与Pn震相的走时差。
当震源位于下地壳时(图 2):
| $ \begin{gathered} \Delta t= \frac{h_{1} \cdot v_{3}}{v_{\mathrm{S}_{2}} \cdot \sqrt{v_{3}^{2}-v_{\mathrm{S}_{2}}^{2}}}+\frac{H_{1} \cdot v_{3}}{v_{\mathrm{S}_{1}} \cdot \sqrt{v_{3}^{2}-v_{\mathrm{S}_{1}}^{2}}}+\\ \frac{H_{1} \cdot v_{3}}{v_{1} \cdot \sqrt{v_{3}^{2}-v_{1}^{2}}}+\frac{h_{1} \cdot v_{3}}{v_{2} \cdot \sqrt{v_{3}^{2}-v_{2}^{2}}}\\ \frac{1}{v_{3}}\left[\frac{h_{1} \cdot v_{2}}{\sqrt{v_{3}^{2}-v_{2}^{2}}}+\frac{H_{1} \cdot v_{1}}{\sqrt{v_{3}^{2}-v_{1}^{2}}}+\right. \\ \left.\frac{h_{1} \cdot v_{\mathrm{S}_{2}}}{\sqrt{v_{3}^{2}-v_{\mathrm{S}_{2}}^{2}}}+\frac{H_{1} \cdot v_{\mathrm{S}_{1}}}{\sqrt{v_{3}^{2}-v_{\mathrm{S}_{1}}^{2}}}\right] \end{gathered} $ | (2) |

|
图 2 双层模型sPn传播路径(震源在下地壳) Fig. 2 The porpagation path of sPn in double-layer model(epicenter in lower crust) |
式中, h1表示震源与上地壳和下地壳分界面的距离,其余量的意义同式(1)。
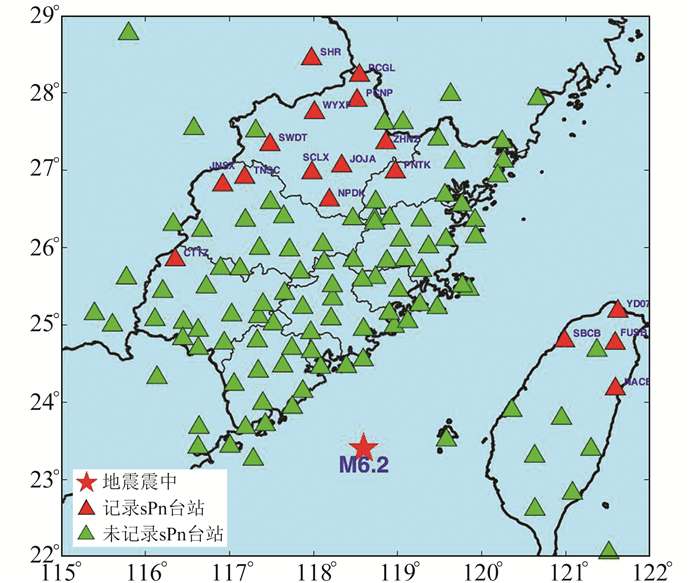
2 数据选取福建台网(图 3)完整记录了此次M6.2地震的过程。福建台网由88个测震台站、16个台湾交换台以及20个江西、广东、浙江共享台组成。经过分析处理,整理出记录到sPn震相的17个震中距大于280 km的台站,此次地震完全具备分辨sPn震相且计算震源深度的能力。
|
图 3 台湾海峡M6.2地震震中和台站分布 Fig. 3 Epicenter of M6.2 Taiwan strait earthquake and distribution of the stations |
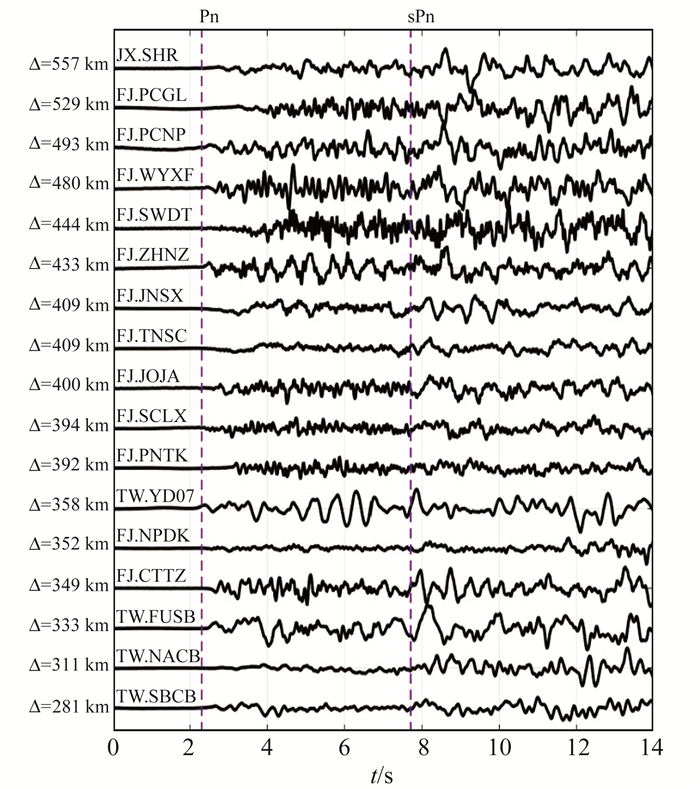
由震相特征得知,sPn震相在垂直分量记录更清晰,因此本文将17个台站垂直分量按不同震中距进行Pn震相对齐排序(图 4),台湾SBCB台是最先识别到sPn震相的台站,排列在波形图最下方,距离震中281 km;江西上饶台相对这些台站是最后识别到较清晰sPn震相的台站,排列在波形图最上方,距离震中557 km。由于sPn与Pn同属于首波性质,分析17个台站的波形记录发现,初动振幅都较微弱,到时位置模糊,只有少数台站能识别出sPn震相,无法避免人为拾取sPn震相的到时误差,所以精确度不够,无法精确测定台湾海峡M6.2的震源深度。
|
图 4 17个台站的波形记录 Fig. 4 Waveforms recordings of 17 stations |
为了提高sPn与Pn震相的走时差测定的准确性,本文采用波形互相关技术获得Pn震相准确到时,然后应用滑动时窗相关法来获取sPn与Pn震相的走时差,进而精确测定台湾海峡主震的震源深度。
3 研究方法与模型选取 3.1 研究方法波形互相关技术是比较2个信号序列相似程度的有效方法,在处理地震数据时,互相关函数被广泛地应用于地震信号检测和震相到时的准确拾取。为了避免人工拾取震相到时误差,本研究采用波形互相方法对齐Pn震相[6-9]。
以时域为例,假设一个地震事件有N条波形记录,对于其中的一对波形i和j的震相到时差tij为:
| $ C_{i j}\left(t_{i j}\right)=\max _{t} C_{i j}(t) $ | (3) |
其中,
| $ C_{i j}(t)=a_{i}^{-1} a_{j}^{-1} \int u_{i}\left(t^{\prime}\right) u_{j}\left(t^{\prime}-t\right) \mathrm{d} t^{\prime} $ | (4) |
| $ a_{i}^{2}=\int u_{i}^{2}\left(t^{\prime}\right) \mathrm{d} t^{\prime} $ | (5) |
式中,Cij是一个地震事件在不同台站记录到的震相波形ui和uj的相关系数。当2条波形完全相同时,maxCij为1;完全不同时,则其逼近于0。Cij为关于到时差t的函数(t的范围即震相互相关窗口),当Cij达到最大值时,tij即为2条波形通过互相关确定的到时差。
滑动时窗相关法可避免发震时刻和震中定位误差的影响,常常用来估计信号之间相关性大小随时间变化的程度。为了提高sPn-Pn测定的准确性,本研究应用滑动时窗相关法来提取sPn震相[6-7]。其原理是,对于一个地震事件的2条波形记录,从某一起始时间计算一定时窗范围内的相关性。对于一个地震的N条波形,计算每2个波形的相关系数,最后进行总体叠加。得出的相关系数中,正峰值大小反映波形相同极性的相似度,反之反映波形之间相反极性的相似度。
3.2 模型选取选用金震等[10]根据福建及台湾海峡地区2008~2016年M>1地震以及福建陆域的18次人工爆破实验数据,利用Kissling等[11]提出的最小一维速度结构方法联合反演福建及台湾海峡地区的一维速度模型(表 1)。
|
|
表 1 福建及台湾海峡地区一维速度模型 Tab. 1 1D velocity model for Fujian and Taiwan strait |
将表 1中的参数分别代入式(1)和式(2)进行计算,得到震源位于上地壳时的震源深度为:
| $ h=2.764 \Delta t $ | (6) |
震源位于下地壳时的震源深度为:
| $ h=3.39 \Delta t-4.743 $ | (7) |
震源深度会影响区域地震波的记录,较深地震的波形脉冲性较强。台湾省气象局发布的震源深度为12.3 km,结合图 4初步得出,台湾海峡M6.2地震的震源深度较浅。因此,本文采用走时方程式(1)进行计算。
4 计算结果分析与对比根据上文17条记录到sPn震相的垂直通道,利用互相关技术筛选出8条波形信噪比较高、震中距在3.0°~6.0°、初至震相清晰的垂直向波形资料进行处理。
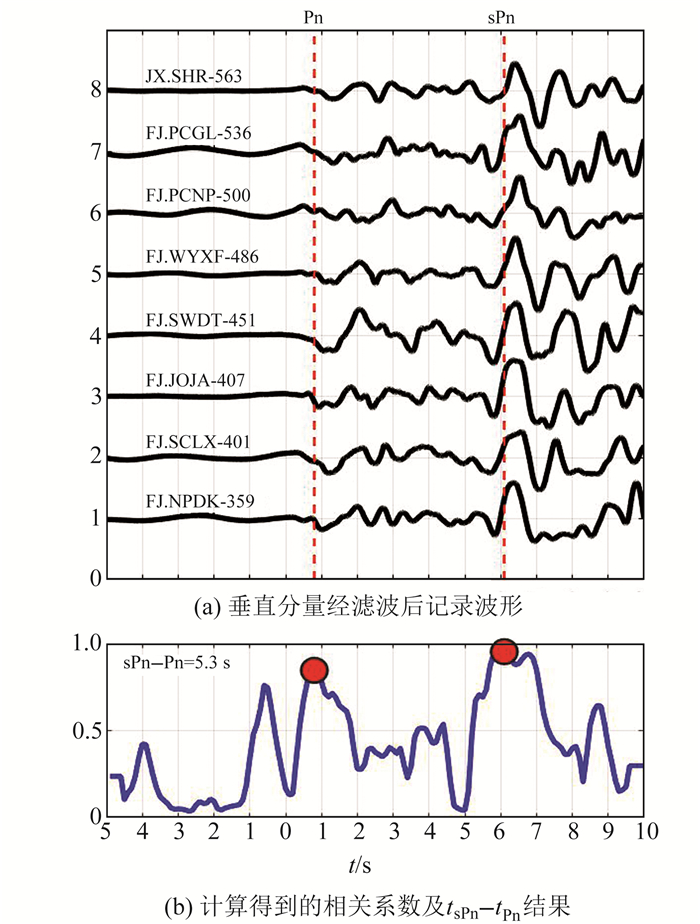
福建台网分布均处于此次海峡主震的北西方向,因此排除不同方位的台站接收到的sPn与Pn震相的走时差问题,只需将8个台站垂直向记录的地震波形去除仪器响应,并进行滤波处理,滤波范围选取0.1~1.0 Hz。然后利用波形互相关技术,把记录到有sPn震相的8个台站初至对齐后,按照震中距大小由下而上排列(图 5(a))。最后利用滑动时窗相关法(取窗长1 s),分别计算每组数据间的互相关系数,并进行叠加来提高相关系数的信噪比,归一化后得到结果(图 5(b))。
|
图 5 垂直分量经滤波后记录波形和计算得到的相关系数及tsPn-tPn结果 Fig. 5 Waveforms recorded by vertical component after filtering and the calculated correlation coefficient and the results of tsPn-tPn |
分析图 5(a)、5(b)得出,8条波形经处理后振幅较明显。在0.8 s有一个较高的峰值,其对应的相关系数为0.92;Pn之后的这个震相经过处理后呈脉冲型,在6.1 s是最高峰,其对应的相关系数为0.98,根据图 5(a)得出波形中的同极性相似度较高,也正好与sPn震相为区域地震P波后面的一个主要震相且振幅相对Pn较大的特性相对应,由此得出第2个峰值就是sPn。图 5(b)搜索出走时差Δt=tsPn-tPn=5.3 s,直接代入式(6)得到海峡M6.2主震的震源深度为14.7 km。
洪星等[12]根据台湾海峡南部一次5.0级地震的sPn震相分析结果认为,用sPn震相计算震源深度时,不同的速度模型对结果影响不大。因此本文不再进行不同速度模型对计算震源深度的影响研究。
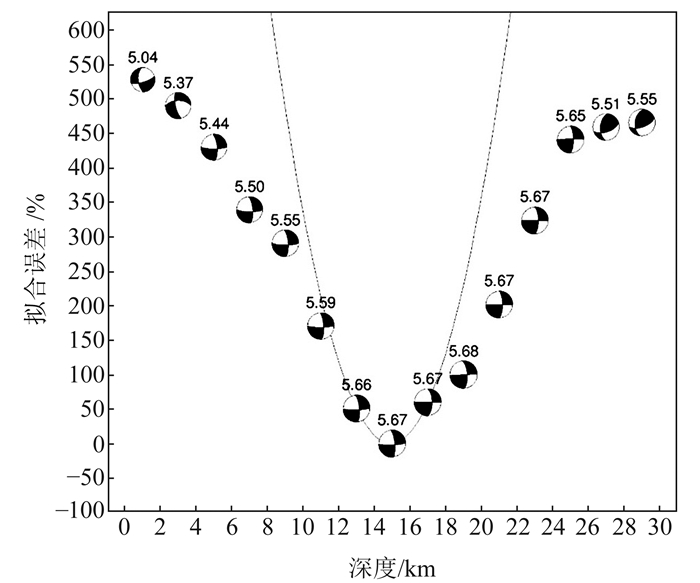
采用近几年来国内较广泛使用的CAP(cut and paste)方法进一步检验前文利用tsPn-tPn求得的震源深度结果的可靠性。CAP方法是一种全波形反演方法,主要将理论地震图和实际观测图进行比对拟合,进而判断出合适的震源机制解和深度[13]。基于这种方法,对台湾海峡M6.2地震事件进行CAP方法反演,其中速度模型采用Crust2.0,速度模型控制参数值设置为1,分别计算出它们的合成波形和真实记录的误差函数,搜索出最佳深度和震源机制解(图 6~8)。
|
图 6 M6.2地震震源深度结果(H=14.9 ± 0.3 km) Fig. 6 Focal depth of M6.2 earthquake (H=14.9 ± 0.3 km) |
|
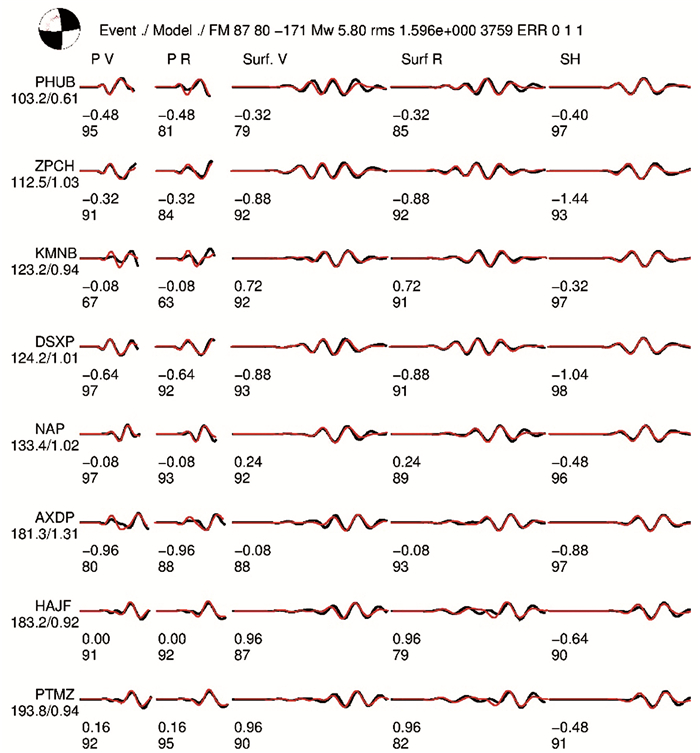
图 7 M6.2地震波形拟合结果 Fig. 7 Seismic waveform fitting results of M6.2 earthquake |
|
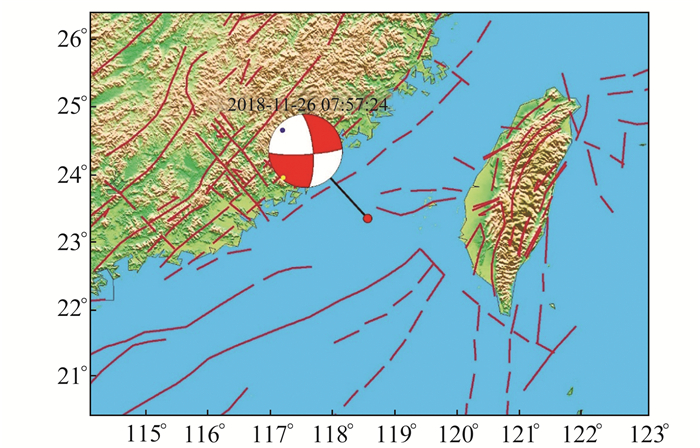
图 8 震源机制解空间分布 Fig. 8 The spatial distribution of the focal mechanism solutions |
图 6为台湾海峡M6.2地震的深度搜索图,深度搜索步长设为2 km。图中曲线即深度拟合曲线,可以看出,深度在10~20 km间的震源机制解基本一致,H=14.9 km为最佳深度值,对应深度拟合曲线中的斜率最大点处的深度,0.3为深度误差(km)。图 7为台湾海峡M6.2地震的波形拟合图(限于篇幅,只提供部分波形拟合图),有13个台站65个震相参与反演,相关系数大于0.8的有47个,占72.2%,理论波形和观测波形拟合度较好,反演质量高,结果可信。图 8为台湾海峡M6.2地震震源机制解空间分布图,可以看出,此次主震以走滑性质为主,最佳双力偶解为:截面1走向87°、倾角82°、滑动角-163°;截面2走向354.6°、倾角73.2°、滑动角-8.4°,最佳深度为14.9±0.3 km。
5 结语本文基于sPn震相测定台湾海峡M6.2地震震源深度,其难度是sPn震相在单台波形中不易识别,易受噪音和尾波的影响。因此本文采用波形互相关技术,应用滑动时窗相关法精确获取sPn与Pn震相的走时差,有效解决了单台挑选的可靠性不高及人为拾取震相存在误差的问题。
利用本文研究方法准确测定出台湾海峡主震的震源深度为14.7 km,与CAP反演方法获得的最佳深度14.9±0.3 km基本一致,进一步证明了本文方法的有效性。且本文方法相对于波形拟合类方法更简捷、易操作,效率也更高。
| [1] |
Chen W P, Nábělek J L, Fitch T J, et al. An Intermediate Depth Earthquake beneath Tibet: Source Characteristics of the Event of September 14, 1976[J]. Journal of Geophysical Research: Atmospheres, 1981, 86(B4): 2 863-2 876 DOI:10.1029/JB086iB04p02863
(  0) 0) |
| [2] |
高原, 周蕙兰, 郑斯华, 等. 测定震源深度的意义的初步讨论[J]. 中国地震, 1997, 13(4): 321-329 (Gao Yuan, Zhou Huilan, Zheng Sihua, et al. Preliminary Discussion on Implication of Determination on Source Depth of Earthquake[J]. Earthquake Research in China, 1997, 13(4): 321-329)
(  0) 0) |
| [3] |
魏娅玲, 蔡一川. 采用sPn震相确定四川长宁地区M≥4.0地震震源深度[J]. 四川地震, 2014(3): 24-27 (Wei Yaling, Cai Yichuan. Calculation of the Focal Depth of the Sichuan Changning M≥4.0 Earthquakes Based on sPn Seismic Phases[J]. Earthquake Research in Sichuan, 2014(3): 24-27)
(  0) 0) |
| [4] |
Ma S T, Atkinson G M. Focal Depths for Small to Moderate Earthquakes (mN≥2.8) in Western Quebec, Southern Ontario, and Northern New York[J]. ulletin of the Seismological Society of America, 2006, 96(2): 609-623 DOI:10.1785/0120040192
(  0) 0) |
| [5] |
张瑞青, 吴庆举, 李永华, 等. 汶川中强余震震源深度的确定及其意义[J]. 中国科学: 地球科学, 2008, 38(10): 1 234-1 241 (Zhang Ruiqing, Wu Qingju, Li Yonghua, et al. Focal Depths for Moderate Sized Aftershocks of the Wenchuan Earthquake and Their Implication[J]. Science China: Earth Sciences, 2008, 38(10): 1 234-1 241)
(  0) 0) |
| [6] |
Laurent G, Davidowitz H. Encoding of Olfactory Information with Oscillating Neural Assemblies[J]. Science, 1994, 1 872-1 875
(  0) 0) |
| [7] |
Laurent G, Wehr M, Davidowitz H. Temporal Representations of Odors in an Olfactory Network[J]. The Journal of Neuroscience, 1996, 16(12): 3 837-3 847 DOI:10.1523/JNEUROSCI.16-12-03837.1996
(  0) 0) |
| [8] |
Saikia C K. A Method for Path Calibration Using Regional and Teleseismic Broadband Seismograms: Application to the 21 May 1997 Jabalpur, India Earthquake(MW5.8)[J]. Seismology, 2000, 79(9): 1 301-1 315
(  0) 0) |
| [9] |
孙茁, 吴建平, 房立华, 等. 利用sPn震相测定芦山MS7.0级地震余震的震源深度[J]. 地球物理学报, 2014, 57(2): 430-440 (Sun Zhuo, Wu Jianping, Fang Lihua, et al. Focal Depth Determination of Aftershocks of Lushan MS7.0 Earthquake from sPn Phase[J]. Chinese Journal of Geophysics, 2014, 57(2): 430-440)
(  0) 0) |
| [10] |
金震, 李山有, 蔡辉腾, 等. 福建及台湾海峡西侧地壳一维速度结构研究[J]. 地震工程与工程振动, 2018, 38(3): 81-93 (Jin Zhen, Li Shanyou, Cai Huiteng, et al. Inversion for the 1D Velocity Model of Onshore-Offshore in Fujian Area[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(3): 81-93)
(  0) 0) |
| [11] |
Kissling E, Ellsworth W L, Eberhart-Phillips D, et al. Initial Reference Models in Local Earthquake Tomography[J]. Journal of Geophysical Research: Solid Earth, 1994, 99(B10): 19 635-19 646 DOI:10.1029/93JB03138
(  0) 0) |
| [12] |
洪星, 叶雯燕, 邵平荣, 等. 台湾海峡南部一次5.0级地震的sPn震相分析[J]. 地震地磁观测与研究, 2006, 27(1): 26-31 (Hong Xing, Ye Wenyan, Shao Pingrong, et al. sPn Seismic Phase Analysis for a ML5.0 Earthquake in Southern Taiwan Strait[J]. Seismological and Geomagnetic Observation and Research, 2006, 27(1): 26-31 DOI:10.3969/j.issn.1003-3246.2006.01.005)
(  0) 0) |
| [13] |
陈惠芳, 段刚, 于培青, 等. 利用福建台网与全球其他台网计算台湾地震震源机制的对比研究[J]. 地震工程学报, 2019, 41(4): 991-998 (Chen Huifang, Duan Gang, Yu Peiqing, et al. A Comparative Study of Focal Mechanism Solutions of Earthquakes in Taiwan Region Calculated by Fujian Seismic Network and Other Seismic Networks[J]. China Earthquake Engineering Journal, 2019, 41(4): 991-998 DOI:10.3969/j.issn.1000-0844.2019.04.991)
(  0) 0) |
2. College of Civil Engineering, Fuzhou University, 2 Xueyuan Road, Fuzhou 350116, China
 2021, Vol. 41
2021, Vol. 41

