相对于同震形变而言,大地震震后形变的持续时间更长、影响范围更广。地震震后形变的研究有助于认识地震的震后形变机制,探索地球深部岩石圈流变结构,为判定后续地震危险性提供重要依据[1]。前人研究结果表明,震后形变机制主要包括发生在地壳浅部的孔隙弹性形变、发生在同震破裂面上的震后余滑形变和发生在下地壳和上地幔的粘弹性松弛形变[2-4]。
据中国地震台网测定,北京时间2015-04-25尼泊尔首都加德满都西北约80 km发生MW7.8地震,震中位于84.70°E、28.20°N,震源深度约为20 km[5-7],美国地质调查局(USGS)通过对全球数字地震台网地震波形数据进行反演,确定了断层破裂模型的滑动幅度和滑动方向,发现此次地震是一次以逆冲为主,兼少量右旋走滑运动的低倾角事件,最大同震位移达到3~4 m。地震发生后,各国研究机构迅速在尼泊尔及其周边地区新增了许多GPS站点,并对旧GPS站点进行复测,获得了大量的震后形变观测资料,为研究震后形变机制提供了数据基础。目前已有的关于尼泊尔地震震后形变机制的研究大多采用的是早期震后形变资料[8-14],研究对象也主要是早期的震后余滑,虽然有部分学者在研究尼泊尔地震震后形变机制时综合考虑了粘弹性松弛效应的影响,但使用的观测数据时间尺度相对较短;部分学者采用了较长时间的震后观测数据,但使用的观测站点较少,无法很好地约束反演模型。因此,本文收集了尼泊尔境内和中国藏南区域共32个GPS连续站震后3 a的观测资料,采用对数函数模型对位移时间序列进行拟合,分离区域构造运动和同震、余震活动的影响,获得尼泊尔地震震后3 a的累积形变场,再分别使用孔隙弹性回弹模型、震后余滑模型、粘弹性松弛模型和组合机制模型研究尼泊尔地震的震后形变机理。
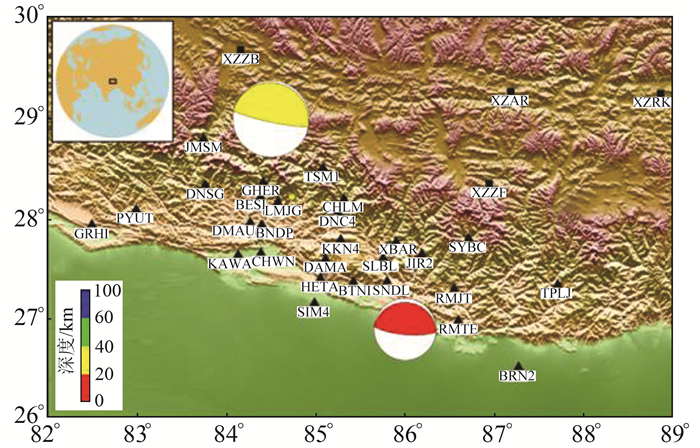
1 震后GPS观测数据处理本文收集了美国内华达州大地测量实验室(http://geodesy.unr.edu/)处理的尼泊尔境内28个测站的原始观测数据及中国地震局GNSS数据产品服务平台(http://www.cgps.ac.cn)处理的中国藏南区域4个测站的原始观测数据。图 1为32个测站的位置分布,图中的震源机制球分别为USGS测定的尼泊尔地震主震和最大余震的震中位置,黑色三角形为尼泊尔境内测站,黑色正方形为中国境内测站。
|
图 1 测站分布 Fig. 1 Distribution of the stations |
GPS时间序列中主要包含构造运动信号、非构造运动信号和季节性周期信号,其中非构造运动信号包含地震的同震和震后形变及其他因素引起的形变,一般可用式(1)表示:
| $ \begin{gathered} y\left(t_{i}\right)=y_{0}+v t_{i}+A \sin \left(2 {\rm{ \mathsf{ π} }} t_{i}\right)+B \cos \left(2 {\rm{ \mathsf{ π} }} t_{i}\right)+ \\ C \sin \left(4 {\rm{ \mathsf{ π} }} t_{i}\right)+D \cos \left(4 {\rm{ \mathsf{ π} }} t_{i}\right)+\sum\limits_{j=1}^{m} E_{j} H\left(t_{i}-t_{c j}\right)+ \\ F \ln \left(1+\left(t_{i}-t_{\mathrm{eq}}\right) / \tau_{i}\right) \end{gathered} $ | (1) |
式中,y(ti)为GPS站点在历元ti时刻的观测值,ti为历元数,v为长期线性速度值,A、B、C、D分别为周期信号振幅,E为由其他原因引起的阶跃,H(ti-tcj)为阶跃函数,F为震后形变振幅,τi为松弛时间常数。其中,F和τi存在较强的负相关性,不能同时估计。
为从原始坐标时间序列中分离出地震的震后形变信号,需要对时间序列中的构造运动信号、季节性周期信号和其他阶跃信号进行修正。由于周期性水平形变的幅度较小,本文在计算尼泊尔地震震后水平形变场时不考虑季节性周期信号的影响。而在构造运动信号获取方面,由于部分GPS测站是震后新增的,没有震前观测数据,可先利用最小二乘参数拟合的方法获取其他测站的震前速度场,再采用克里金插值的方法获得这些新增测站的震前速度场,计算结果见图 2(ITRF2014框架下,图中蓝色箭头表示利用震前时间序列计算的长期运动速率,红色箭头表示利用克里金插值估算的震前运动速率);对于同震及余震产生的阶跃信号的影响,可采用在拟合函数中添加初始常数的方法解决。

|
图 2 震前GPS速度场 Fig. 2 GPS velocity field before the earthquake |
利用计算的震前背景速度场可以对GPS原始坐标时间序列进行构造形变改正,得到改正后的震后坐标时间序列。由于各个GPS测站的观测时段不一,为计算每个测站震后3 a的位移量,需要对改正后的震后坐标时间序列进行函数拟合。本文采用式(2)对数模型进行拟合:
| $ y=F \ln \left(1+\frac{\Delta t}{\tau}\right)+k $ | (2) |
式中,F为震后形变振幅,Δt为震后逝去时间,τ为震后松弛时间,k为去除同震及余震阶跃影响添加的时间序列初始常数。
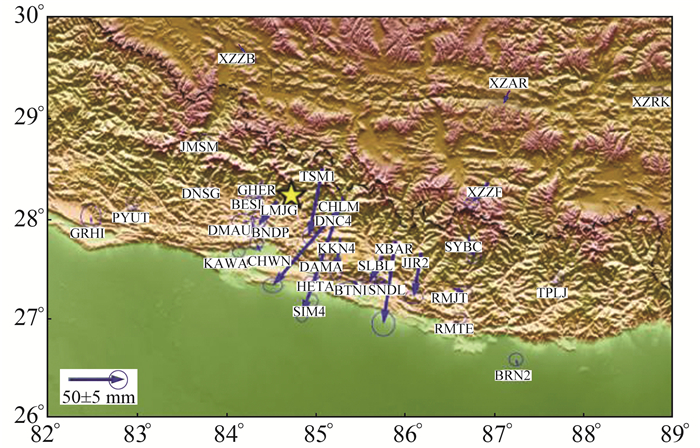
由于F和τ具有较强的负相关性,很难同时反演确定,本文通过大量试算,最终固定τ为38 d,将非线性方程转化为线性方程,拟合每个GPS站的观测分量,拟合的平均水平误差为2.6 mm,计算的震后水平位移如图 3所示。可以看出,震后形变主要集中在尼泊尔北部区域,且东西方向形变较小,南北方向形变较大,整体继续向南运动,最大震后地表水平位移发生在CHLM站,约10.93 cm,为西南方向。
|
图 3 尼泊尔地震震后3 a水平形变场 Fig. 3 Horizontal postseismic deformation field three years after Nepal earthquake |
一般来说,地球介质中都会有小到分子量级的孔隙,而这些孔隙的存在可以使某些分子顺利通过,这种存在大量密集微小孔隙的固体物质被称为孔隙介质或多孔介质。地震发生前,地壳介质处于未排空水状态;地震发生时,累积的地震应变能量迅速爆发,断层发生破裂,导致周围的孔隙水压力升高,岩体中孔隙水的平衡状态被破坏;震后短时间内孔隙水由高压力地区不断流向低压力地区,孔隙水压再次恢复到另一种平衡状态[15]。在这个过程中,孔隙水的流动使岩石间的应力发生变化,进而导致地表形变或发生余震。
考虑到孔隙流体的反弹时间尺度非常依赖于岩石的可渗透率,通常会持续数月到数年,且其时间衰减是非线性的,使得孔隙回弹形变的计算过程非常复杂。因此,通常利用同震破裂模型分别计算地震在未排空水状态和完全排空水状态下产生的地表形变,两者的差值即可近似为孔隙弹性回弹造成的地表形变,具体计算公式为:
| $ u_{i}(x)=u_{i}\left(t_{q}, v\right)-u_{i}\left(t_{q}, v_{u}\right) $ | (3) |
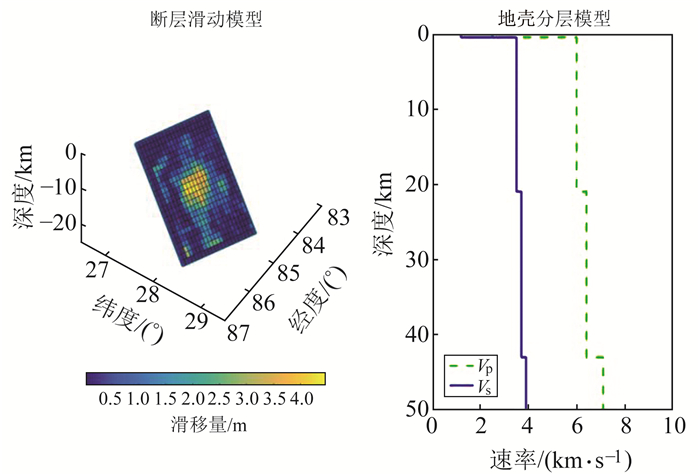
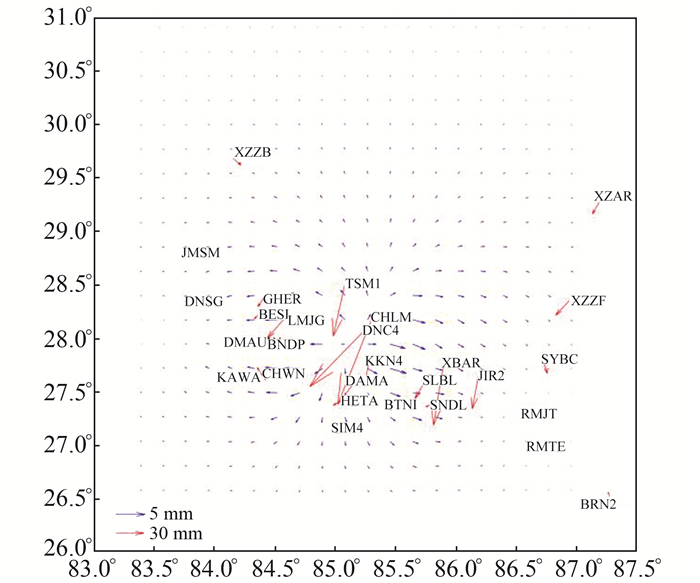
式中,ui(x)为x点在i方向上的位移,ui(tq, v)和ui(tq, vu)分别为未排空水状态和完全排空水状态下计算得到的地表形变。假定未排空水状态下的泊松比为0.27,完全排空水状态下的泊松比为0.25,采用Hayes等[16]公布的同震破裂模型和地壳分层模型(图 4)分别计算2种状态下的地表形变,并对其进行差分,得到孔隙弹性回弹引起的地表位移场,计算结果见图 5(图中红色箭头表示GPS观测的震后3 a位移,蓝色箭头表示孔隙弹性回弹引起的地表理论位移)。
|
图 4 断层滑动模型与地壳分层模型 Fig. 4 Fault slip model and crust model |
|
图 5 孔隙弹性回弹引起的地表形变 Fig. 5 Surface deformation induced by poroelastic rebound |
从图 5可以看出,孔隙弹性回弹引起的地表理论位移主要集中在同震破裂周围,最大形变量约为2.8 mm(27.72°N,85.46°E),向四周呈发散状,且离震中区域越远,形变量越小。此外,通过对比孔隙弹性回弹引起的地表理论位移与GPS观测的震后形变值可以发现,在多数站点二者没有一致性,尽管在有些站点二者的运动方向一致,但孔隙弹性回弹产生的形变量远小于GPS观测值。因此可以认为,使用该模型不能解释尼泊尔地震的震后形变,且由于孔隙弹性回弹引起的地表位移贡献量较小,在后续研究中不予考虑。
3 震后余滑模型设置反演的目标函数为[10]:
| $ F(\boldsymbol{s}, \beta)=\|\boldsymbol{W}(G \boldsymbol{s}-\boldsymbol{d})\|^{2}+\beta^{2}\left\|\nabla^{2} \boldsymbol{s}\right\|^{2} $ | (4) |
式中,W为观测值的权矩阵,G为格林函数,d为震后位移观测值,s为滑动量,β为平滑因子,用于调节模型粗糙度和数据拟合误差之间的关系,
本文采用熊维等[17]的研究成果建立尼泊尔地区地壳分层模型,以计算点源单位滑动对地表形变场的映射格林函数,具体参数见表 1。
|
|
表 1 尼泊尔地区地壳结构模型 Tab. 1 Crustal structure model in Nepal |
根据表 1的地壳分层模型,采用SDM程序附带的格林函数计算程序,基于分层半无限空间模型计算尼泊尔地区的位移格林函数。
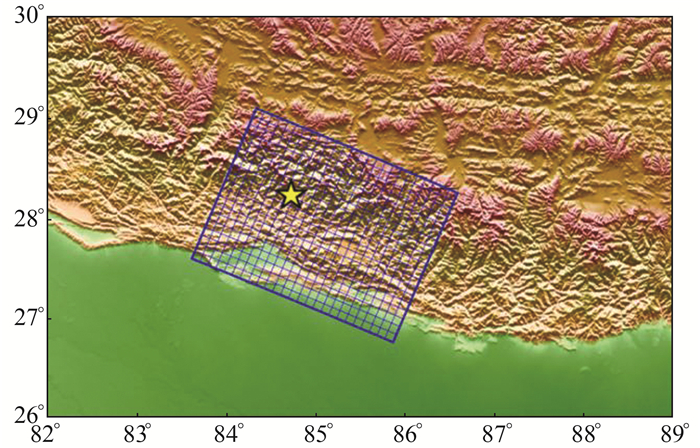
3.2 断层模型由于震后余滑通常发生在同震破裂面或其延伸面区域,因此在构建震后余滑反演模型时可以以同震破裂模型为基础,并在长度和宽度上进行适当延伸,以保证其能覆盖整个震后余滑的空间范围。本文以Hayes等[16]的同震破裂模型为基础,取长度为260 km、宽度为200 km,并将其沿断层走向和倾向离散成26×20个10 km×10 km的子断层,具体模型参数见表 2。断层模型的实际地理位置如图 6所示。
|
|
表 2 预设断层模型参数 Tab. 2 Preset fault model parameters |
|
图 6 有限断层模型 Fig. 6 Finite fault model |
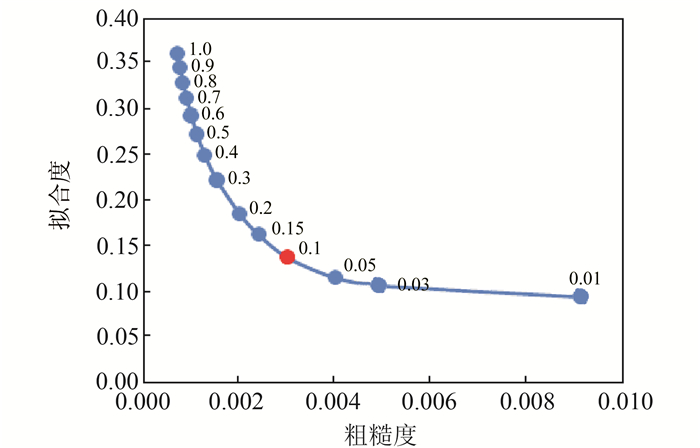
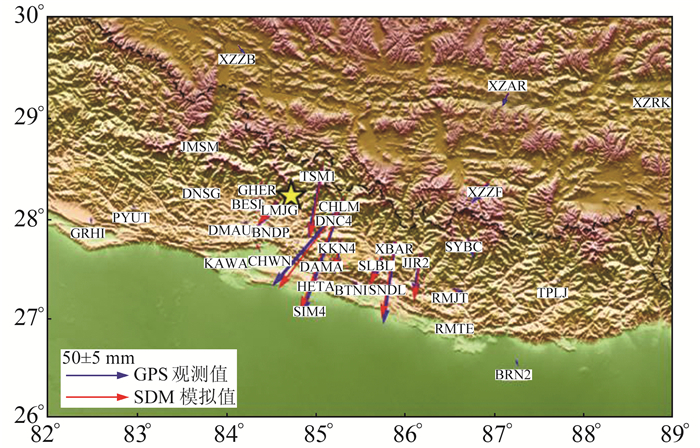
基于§3.1地壳分层模型计算的格林函数和断层模型参数,采用SDM反演程序对震后的断层余滑分布进行反演,反演过程中需要不断调整平滑因子,以平衡模型粗糙度和数据拟合误差之间的关系。图 7为余滑模型的模型粗糙度和数据拟合误差的折中曲线(图中圆点旁边的数字为对应的平滑因子),可以看出,当β=0.1时可较好地平衡模型粗糙度和数据拟合误差之间的关系,此时模型值与观测值的拟合误差为2.71 mm。从图 8可以看出,震后余滑模型可较好地解释GPS观测的震后地表水平位移。
|
图 7 余滑模型的模型粗糙度与数据拟合误差折中曲线 Fig. 7 Compromise curve between model roughness and data misfit of the afterslip model |
|
图 8 GPS观测值与震后余滑模型模拟值对比 Fig. 8 Comparison between GPS observation and post earthquake residual slip model simulation |
对应的震后余滑模型见图 9,可以看出,反演的平均滑动量约为8.6 cm,最大滑动量为34.39 cm,位于地下约26.6 km处, 震后余滑释放的地震矩为1.09×1020 Nm,对应的矩震级为MW7.33。对比同震破裂模型可以看出,震后余滑在浅部同震未破裂区域的分布极其有限,主要分布在20~30 km的同震破裂面下倾延伸部分,且分布范围广泛。Mencin等[18]采用应力驱动余滑模型反演的震后余滑发生在同震破裂面的正下方,而出现这种模型断层底端滑动的现象可能是由于忽略了粘弹性松弛效应导致的。

|
图 9 断层滑动三维及二维梯度 Fig. 9 Three-dimensional map of fault slip and two-dimensional gradient |
下地壳和上地幔的物质并不是完全的弹性体,通常视为粘性流体。地震发生后,受到同震和震后应力变化的影响,具有粘弹性质的中下地壳和上地幔应力状态随时间缓慢变化,使得上地壳的弹性层发生应力扰动,进而引发大范围的地表形变,这种震后形变称为震后粘弹性松弛。由于粘弹性松弛效应引起的震后形变的空间尺度和时间尺度都较大,因此在进行震后余滑反演时需要考虑其影响,否则会高估断层深部的震后余滑[19]。
4.1 地壳分层模型地震造成的震后粘弹性形变与上地壳弹性层厚度和粘弹性层粘滞系数的大小有很大的关系,当弹性层厚度越薄,也就是粘弹性层越接近地表或者粘滞系数越小时,震后产生的地表形变就越大,反之亦然。根据徐晶等[20]和万永革等[21]的研究,青藏高原中下地壳的粘滞系数在1019~1020 Pa·s之间,上地幔粘滞系数约为1.0×1020 Pa·s,由此可确定尼泊尔地区的地壳分层模型:0~20 km为上地壳弹性层;20~51 km为中下地壳;51 km以下为上地幔及以下区域。使用Maxwell流体模拟中下地壳和上地幔的流变结构,其中,中下地壳的粘滞系数取1.0×1019 Pa·s,上地幔的粘滞系数取1.0×1020 Pa·s。
4.2 断层模型使用Hayes等[16]的同震断层滑动分布模型(图 4),断层几何参数为:走向293°,倾角7°,顶部埋深4.3 km,沿走向和倾向划分为等间隔的23×24块子断层,分割成约8.4 km×7 km的子断层块,覆盖范围约193.2 km×168 km。
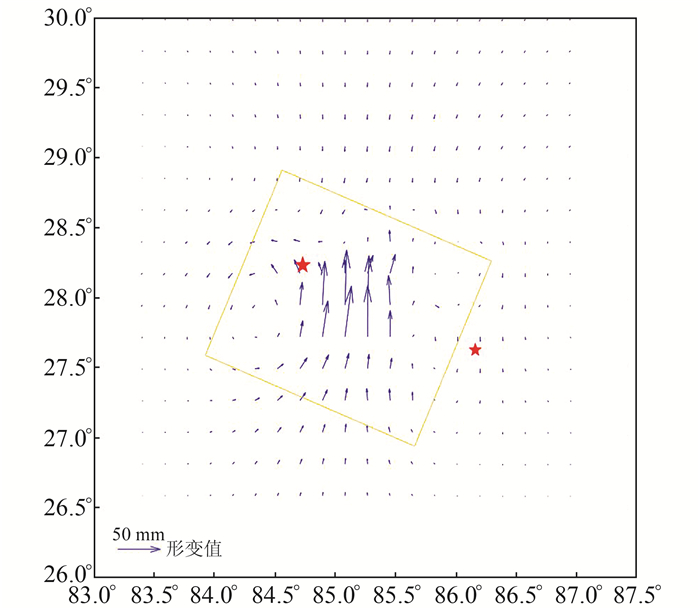
4.3 震后形变模拟使用Wang等[22]的PSGRN/PSCMP程序,基于§4.1的地壳分层模型和Hyaes等[6]的同震破裂模型计算粘弹性松弛引起的震后地表形变,计算结果见图 10(图中,蓝色箭头代表粘弹性松弛引起的地表形变理论值,红色五角星表示同震震中和余震震中,黄色方框表示同震破裂模型)。从图 10可以看出,粘弹性松弛引起的地表形变主要分布在同震破裂区域,最大位移量约为7.9 cm(27.95°N,85.08°E),整体表现为向北的运动趋势,与同震破裂面引起的地表形变变化趋势相反,但在同震破裂面的南部远场区域向北运动,在同震破裂面的北部远场区域向南运动,与同震引起的形变运动方向基本一致。
|
图 10 粘弹性松弛引起的地表形变 Fig. 10 Surficial deformation caused by viscoelastic relaxation |
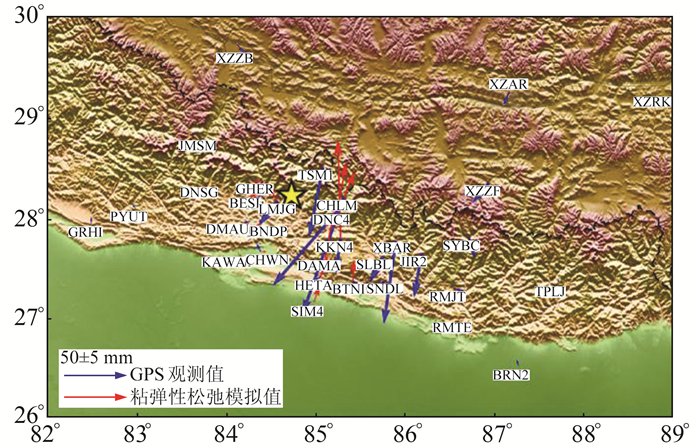
图 11为震后3 a的GPS观测值与粘弹性松弛模拟值的对比。可以看出,震后形变中,粘弹性松弛模型并不能解释近场的地表形变,其远场形变的运动方向与GPS观测值一致,但形变量小于GPS观测值,这可能是由尼泊尔地区和青藏高原地区地球模型的横向不均匀性导致的。
|
图 11 震后3 a累积形变值与粘弹性松弛模拟值比较 Fig. 11 Comparison between observed postseismic displacements in three years after earthquake and predicted viscoelastic displacements |
本文分别使用孔隙弹性回弹模型、粘弹性松弛模型和震后余滑模型来解释GPS观测到的震后形变。结果发现,单独的震后形变机理并不能合理地解释尼泊尔地震的GPS观测资料,其中孔隙弹性回弹引起的地表形变作用范围和量级均较小,无法解释GPS观测的震后形变;粘弹性松弛模型则可以解释远场的GPS观测值,但同样无法解释近场的地表形变;震后余滑模型的拟合程度最高,但反演的震后余滑主要分布在同震破裂的下倾延伸部分,最大余滑深度接近地下30 km,且分布范围广泛。
因此,为同时兼顾近场、远场、拟合误差和物理意义,本文采用震后余滑+粘弹性松弛组合机制模型进行研究。首先从图 3的GPS观测值中扣除图 11中粘弹性松弛引起的理论地表形变,然后以修正过的GPS观测值为约束条件,结合§3的地壳分层模型和断层滑动模型,利用SDM反演程序重新反演震后余滑分布模型。
图 12为去除粘弹性的余滑模型的模型粗糙度与数据拟合误差的折中曲线。可以看出,β=0.1为最佳光滑因子,此时的观测值与模拟值的拟合误差为2.72 mm。从图 13可以看出,组合机制模型同样可以很好地解释震后GPS观测值。

|
图 12 去除粘弹性后余滑模型的模型粗糙度与数据拟合误差的折中曲线 Fig. 12 Compromise curve between model roughness and data fitting error of residual slip model excluding viscoelasticity |

|
图 13 扣除粘弹性的GPS观测值与模拟值对比 Fig. 13 Comparison of GPS observations and simulated values excluding viscoelasticity |
图 14为经粘弹性松弛修正后的震后余滑模型。可以看出,修正后的震后余滑主要集中在17~26 km的同震破裂下倾部分,反演的最大滑动量为38.67 cm,深度约为21.17 km,整个断层面的平均滑动量约为8.5 cm,震后余滑释放的地震矩也下降到1.08×1020 Nm,对应的矩震级为MW7.32。修正后的震后余滑模型在保证数据拟合度的基础上,平均滑动量和地震矩较修正前都有所降低,且在空间分布上也有所升高和集中,这与Mencin等[18]采用应力驱动模型反演的结果更接近。

|
图 14 去除粘弹性后断层滑动三维及二维梯度 Fig. 14 Three-dimensional and two-dimensional ladder of fault slip excluding viscoelasticity |
本文收集2015年尼泊尔MW7.8地震震区附近的GPS连续站观测资料,获取尼泊尔地震震后3 a的水平形变场,并以此为约束,分别采用孔隙弹性回弹模型、震后余滑模型、粘弹性松弛模型和组合机制模型研究尼泊尔地震的震后形变机制。结果表明:
1) GPS观测到的尼泊尔地震震后形变主要集中在尼泊尔北部区域,且东西方向形变较小,南北方向形变较大,整体向南运动。地表最大震后位移发生在CHLM站,约为10.93 cm,向西南方向。
2) 分别采用孔隙弹性回弹模型、震后余滑模型和粘弹性松弛模型研究尼泊尔地震的震后形变机理,模拟结果显示,孔隙弹性回弹模型模拟计算的理论地表形变空间分布范围较小,且远小于GPS观测的震后形变;SDM程序反演的震后余滑模型虽然可以较好地拟合GPS观测值,但反演的震后余滑分布范围广泛,且主要集中在同震破裂面的下倾延伸部分;PSGRN/PSCMP程序计算的粘弹性松弛引起的理论地表形变无法解释近场形变,只有在远场区域其运动方向才与GPS观测值一致,这可能是尼泊尔地区和青藏高原地区地球模型的横向不均匀性导致的。
3) 利用震后余滑和粘弹性松弛的组合机制模型研究尼泊尔地震的震后形变机制后发现,组合机制模型在保证数据拟合度的基础上,其平均滑动量和地震矩较修正前都有所降低,且在空间分布上也有所升高和集中,与应力驱动模型的反演结果更为接近。
4) 组合机制模型反演的震后余滑主要发生在同震破裂面下倾部分,而同震未破裂断层的浅部未检测到滑动信息,说明断层浅部未发生破裂,未来的地震危险性较高。
| [1] |
孟国杰, 苏小宁, 徐婉桢, 等. 基于GPS观测研究2010年青海玉树MS7.1地震震后地壳形变特征及其机制[J]. 地球物理学报, 2016, 59(12): 4 570-4 583 (Meng Guojie, Su Xiaoning, Xu Wanzhen, et al. Postseismic Deformation Associated with the 2010 Yushu, Qinghai MS7.1 Earthquake by GPS Observations[J]. Chinese Journal of Geophysics, 2016, 59(12): 4 570-4 583)
(  0) 0) |
| [2] |
Azúa B M, DeMets C, Masterlark T. Strong Interseismic Coupling, Fault Afterslip, and Viscoelastic Flow before and after the Oct 9, 1995 Colima-Jalisco Earthquake: Continuous GPS Measurements from Colima, Mexico[J]. Geophysical Research Letters, 2002, 29(8): 1-4
(  0) 0) |
| [3] |
Barbot S, Fialko Y. A Unified Continuum Representation of Post-Seismic Relaxation Mechanisms: Semi-Analytic Models of Afterslip, Poroelastic Rebound and Viscoelastic Flow[J]. Geophysical Journal International, 2010, 182(3): 1 124-1 140 DOI:10.1111/j.1365-246X.2010.04678.x
(  0) 0) |
| [4] |
Bedford J, Moreno M, Li S Y, et al. Separating Rapid Relocking, Afterslip, and Viscoelastic Relaxation: An Application of the Postseismic Straightening Method to the Maule 2010 CGPS[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(10): 7 618-7 638 DOI:10.1002/2016JB013093
(  0) 0) |
| [5] |
张勇, 许力生, 陈运泰. 2015年尼泊尔MW7.9地震破裂过程: 快速反演与初步联合反演[J]. 地球物理学报, 2015, 58(5): 1 804-1 811 (Zhang Yong, Xu Lisheng, Chen Yuntai. Rupture Process of the 2015 Nepal MW7.9 Earthquake: Fast Inversion and Preliminary Joint Inversion[J]. Chinese Journal of Geophysics, 2015, 58(5): 1 804-1 811)
(  0) 0) |
| [6] |
张贝, 程惠红, 石耀霖. 2015年4月25日尼泊尔MS8.1大地震的同震效应[J]. 地球物理学报, 2015, 58(5): 1 794-1 803 (Zhang Bei, Cheng Huihong, Shi Yaolin. Calculation of the Co-Seismic Effect of MS8.1 Earthquake, Apirl 25, 2015, Nepal[J]. Chinese Journal of Geophysics, 2015, 58(5): 1 794-1 803)
(  0) 0) |
| [7] |
赵斌, 杜瑞林, 张锐, 等. GPS测定的尼泊尔MW7.9和MW7.3地震同震形变场[J]. 科学通报, 2015, 60(增2): 2 758-2 766 (Zhao Bin, Du Ruilin, Zhang Rui, et al. Co-Seismic Displacements Associated with the 2015 Nepal MW7.9 Earthquake and MW7.3 Aftershock Constrained by Global Positioning System Measurements[J]. Chinese Science Bulletin, 2015, 60(S2): 2 758-2 766)
(  0) 0) |
| [8] |
王东振, 赵斌, 余建胜, 等. 利用GPS观测资料分析2015年尼泊尔MS8.1地震震前及震后形变[J]. 大地测量与地球动力学, 2017, 37(6): 579-584 (Wang Dongzhen, Zhao Bin, Yu Jiansheng, et al. Pre- and Post-Seismic Deformation of Nepal MS8.1 Earthquake Derived from GPS Data[J]. Journal of Geodesy and Geodynamics, 2017, 37(6): 579-584)
(  0) 0) |
| [9] |
Sreejith K M, Sunil P S, Agrawal R, et al. Coseismic and Early Postseismic Deformation Due to the 25 April 2015 MW7.8 Gorkha, Nepal, Earthquake from InSAR and GPS Measurements[J]. Geophysical Research Letters, 2016, 43(7): 3 160-3 168 DOI:10.1002/2016GL067907
(  0) 0) |
| [10] |
赵斌, 王东振, 谭凯, 等. 顾及粘弹性松弛效应的2015年尼泊尔MW7.9地震震后早期余滑模型[J]. 大地测量与地球动力学, 2018, 38(3): 239-243 (Zhao Bin, Wang Dongzhen, Tan Kai, et al. Afterslip Model Following the 2015 Nepal MW7.9 Earthquake Considering Viscoelastic Relaxation Displacements[J]. Journal of Geodesy and Geodynamics, 2018, 38(3): 239-243)
(  0) 0) |
| [11] |
李宇磊, 张永志, 王帅, 等. 2015年尼泊尔MW7.8地震的震后形变机制: 震后余滑效应和粘滞性松弛效应[J]. 武汉大学学报: 信息科学版, 2020, 45(10): 1578-1587 (Li Yulei, Zhang Yongzhi, Wang Shuai, et al. Post-Seismic Deformation Processes: Afterslip and Vicoelastic Relaxation Following the 2015 Nepal MW7.8 Earthquake[J]. Geomatics and Information Science of Wuhan University, 2020, 45(10): 1578-1587)
(  0) 0) |
| [12] |
Wang K, Fialko Y. Observations and Modeling of Coseismic and Postseismic Deformation Due to the 2015 MW7.8 Gorkha(Nepal) Earthquake[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(1): 761-779 DOI:10.1002/2017JB014620
(  0) 0) |
| [13] |
苏小宁, 孟国杰. 基于GPS观测的2015年尼泊尔MS8.1地震多尺度震后形变特征[J]. 地震, 2018, 38(4): 1-13 (Su Xiaoning, Meng Guojie. Multiscale Postseismic Deformation Based on GPS Time Series Following the 2015 Gorkha Nepal MS8[J]. Earthquake, 2018, 38(4): 1-13)
(  0) 0) |
| [14] |
Tian Z, Freymueller J T, Yang Z Q. Spatio-Temporal Variations of Afterslip and Viscoelastic Relaxation Following the MW7.8 Gorkha(Nepal) Earthquake[J]. Earth and Planetary Science Letters, 2020, 532
(  0) 0) |
| [15] |
Jónsson S, Segall P, Pedersen R, et al. Post-Earthquake Ground Movements Correlated to Pore-Pressure Transients[J]. Nature, 2003, 424(6 945): 179-183
(  0) 0) |
| [16] |
Hayes G P, Briggs R W, Barnhart W D, et al. Rapid Characterization of the 2015 MW7.8 Gorkha, Nepal, Earthquake Sequence and Its Seismotectonic Context[J]. Seismological Research Letters, 2015, 86(6): 1 557-1 567 DOI:10.1785/0220150145
(  0) 0) |
| [17] |
熊维, 谭凯, 刘刚, 等. 2015年尼泊尔MW7.9地震对青藏高原活动断裂同震、震后应力影响[J]. 地球物理学报, 2015, 58(11): 4 305-4 316 (Xiong Wei, Tan Kai, Liu Gang, et al. Coseismic and Postseismic Coulomb Stress Changes on Surrounding Major Faults Caused by the 2015 Nepal MW7.9 Earthquake[J]. Chinese Journal of Geophysics, 2015, 58(11): 4 305-4 316)
(  0) 0) |
| [18] |
Mencin D, Bendick R, Upreti B N, et al. Himalayan Strain Reservoir Inferred from Limited Afterslip Following the Gorkha Earthquake[J]. Nature Geoscience, 2016, 9(7): 533-537 DOI:10.1038/ngeo2734
(  0) 0) |
| [19] |
Huang M H, Bürgmann R, Freed A M. Probing the Lithospheric Rheology across the Eastern Margin of the Tibetan Plateau[J]. Earth and Planetary Science Letters, 2014, 396: 88-96 DOI:10.1016/j.epsl.2014.04.003
(  0) 0) |
| [20] |
徐晶, 邵志刚, 马宏生, 等. 鲜水河断裂带库仑应力演化与强震间关系[J]. 地球物理学报, 2013, 56(4): 1 146-1 158 (Xu Jing, Shao Zhigang, Ma Hongsheng, et al. Evolution of Coulomb Stress and Stress Interaction among Strong Earthquakes along the Xianshuihe Fault Zone[J]. Chinese Journal of Geophysics, 2013, 56(4): 1 146-1 158)
(  0) 0) |
| [21] |
万永革, 沈正康, 盛书中, 等. 2008年汶川大地震对周围断层的影响[J]. 地震学报, 2009, 31(2): 128-139 (Wan Yongge, Shen Zhengkang, Sheng Shuzhong, et al. The Influence of 2008 Wenchuan Earthquake on Surrounding Faults[J]. Acta Seismologica Sinica, 2009, 31(2): 128-139 DOI:10.3321/j.issn:0253-3782.2009.02.002)
(  0) 0) |
| [22] |
Wang R J, Lorenzo-Martín F, Roth F. PSGRN/PSCMP—A New Code for Calculating Co- and Post-Seismic Deformation, Geoid and Gravity Changes Based on the Viscoelastic-Gravitational Dislocation Theory[J]. Computers and Geosciences, 2006, 32(4): 527-541 DOI:10.1016/j.cageo.2005.08.006
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


