岩石对地球内部力学作用的变形响应取决于岩石的流变属性,而岩石圈及软流圈的粘滞系数是理解板块以及块体边界带演化过程的重要参数[1]。地震可以看作是突然发生的自然岩石力学实验,其引起的应力变化导致下地壳及上地幔粘弹性弛豫,从而使地面发生长期形变[2-3]。目前,采用大地测量技术获取的震后形变已被广泛用于探测地球岩石圈的流变结构[4-5]。
2015-04-25青藏高原南缘的主喜马拉雅逆冲断裂带(main Himalayan thrust, MHT)发生MW7.8地震。该地震还伴随7级以上强余震,其中最大余震发生在主震震中东南约150 km处,矩震级为MW7.3[6-7]。布设在尼泊尔及藏南的GPS台站在震后记录到显著形变,为探测青藏高原南缘下地壳和上地幔流变特性提供了条件,也为进一步认识喜马拉雅逆冲断层的地震演化和青藏高原隆升机制提供了重要参考资料。
尼泊尔MW7.8地震发生后,大量学者利用大地测量资料对该区域的流变结构进行研究[3, 8-9],但使用的GPS观测数据局限于尼泊尔附近,缺少距离震中200 km以外的青藏高原南部地区的数据;且假设的印度板块和青藏高原板块垂直边界过于简单,因此模拟的下地壳及上地幔粘滞系数具有较大的不确定性。另外,尼泊尔-喜马拉雅地区的大地电磁、地震波层析成像、地热结构、有效岩石圈厚度等相关研究显示,喜马拉雅地区两侧的结构具有显著的横向不均匀性[10],而这种特性会对传统解析或半解析方法的结果造成很大影响[8]。有限元模拟方法在解决该类问题上具有较大优势。本文基于更多藏南远场GPS站点震后5 a的观测数据,采用有限元方法模拟尼泊尔地震的震后粘弹性松弛效应,并通过垂直边界和俯冲带结构边界来约束区域下地壳和上地幔的流变特性,该研究对评估喜马拉雅地震带的地震灾害、认识地震机理和岩石圈流变特性具有重大意义。
1 GPS数据与处理 1.1 数据处理本文共收集51个GPS站点的观测数据,其中包含近期新采集的距离破裂区150~250 km的13个位于藏南地区的连续站数据[11]和7个新增的流动站数据。采用GAMIT/GLOBK 10.7版本对所有的原始RINEX数据进行统一处理。首先利用IGS发布的精密星历估计测站坐标、卫星轨道、大气延迟等参数,得到无基准的自由网解;然后采用卡尔曼滤波方法计算区域单日松弛解与全球单日松弛解的组合解,并通过50个IGS追踪站将组合解归算至ITRF2014参考框架。由此得到的坐标时间序列中仍含有因长期构造运动、季节性的周年、半周年周期变化、同震或仪器变更等引起的阶跃信号[3],表达式为:
| $ \begin{array}{c} X(t)=A+B t+C_{1} \sin (2 {\rm{ \mathsf{ π} }} t)+C_{2} \cos (2 {\rm{ \mathsf{ π} }} t)+ \\ C_{3} \sin (4 {\rm{ \mathsf{ π} }} t)+C_{4} \cos (4 {\rm{ \mathsf{ π} }} t)+\sum\limits_{i=1}^{N} D_{i} H(t) \end{array} $ | (1) |
式中,A为震后形变;B为线性运动速率;C1、C2、C3、C4为描述季节性的周年、半周年周期信号的系数;Di为地震同震或仪器变更(如替换天线)等原因引起的阶跃信号;H(t)为阶跃函数。在提取震后形变时应将上述信号从原始时间序列中去除。
对于在尼泊尔地震之前已经开始观测的GPS站,本文直接估算其长期运动速率。部分GPS站由于损坏或在震后才建立,无震前观测数据,无法直接估计其长期运动速率,因此采用内插方法进行计算并从震后形变中去除[12]。此外,采用Zhao等[3]的方法改正2015-05-12 MW7.3余震引起的阶跃项以及季节性的周年、半周年周期变化。经过上述改正,获得每个GPS站点的震后位移时间序列。
1.2 震后形变由于不同测站观测资料时长不同,为得到GPS站点震后5 a的累积位移,对改正后的时间序列采用对数函数进行拟合:
| $ u(t)=a_{1}+a_{2} \ln \left(1+\frac{t-t_{0}}{\tau}\right) $ | (2) |
式中,u(t)为t时刻累积观测位移;a1为常数;a2为震后形变幅度;τ为震后松弛时间。图 1为本文所采用的GPS站点累积5 a的震后位移,其中蓝色箭头代表水平位移,颜色变化代表垂直位移。从图中可以看出,尼泊尔地震引起地面向南-西南方向运动,震后形变主要集中在尼泊尔北部和中尼边界区域,并向北衰减,靠近主前缘断裂带的GPS站点的位移较小。CHLM站的水平位移最大,约为121 mm,NAST站的垂直位移最大,为83 mm。
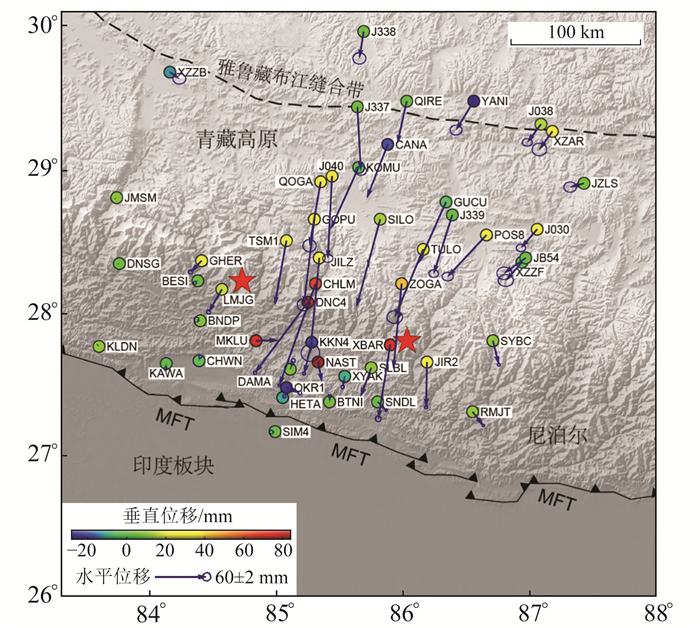
|
图 1 尼泊尔地震构造背景及震后5 a累积位移 Fig. 1 Tectonic setting of the study area and cumulative displacements of 5 years after the Nepal earthquake |
参考Elliott等[13]提出的“双断坡”断层模型,以断层面中心点在地面的投影为笛卡尔坐标系原点,建立三维粘弹性有限元模型(图 2)。模型南北方向长度为2 000 km,东西方向长度为1 500 km,厚度为800 km。为更好地计算断层破裂附近的应力场和位移,首先将断层面划分为边长约5 km的三角形,然后设置格网尺寸随距断层面的距离以1 ∶1的比例因子逐渐增大进行整体划分,最终共划分445 210个四面体单元。模型共包含95 130个节点,最小格网尺寸为5 km,最大格网尺寸为158 km。

|
图 2 有限元模型及格网划分 Fig. 2 The finite element model and grid division |
保持模型侧边界垂直及下边界水平,上边界可进行调整,采用文献[14]中P波和S波速度结构,并设置上地壳、下地壳和上地幔的密度分别为2 700 kg/m3、3 300 kg/m3和3 800 kg/m3。
2.2 岩石圈流变结构配置本文采用2种不同的印度板块与青藏高原板块边界(BL)来构建模型:一种为垂直边界模型(模型1,图 3(a)),另一种为印度弹性俯冲板片模型(模型2,图 3(b))。对于模型1,假设印度板块弹性地壳厚度为50 km,其下是粘滞系数为1×1020 Pa·s的Maxwell粘弹性上地幔;而在青藏高原南部,根据该地区地震震源深度分布,取弹性上地壳厚度为30 km,下地壳由30 km延伸至青藏高原莫霍面平均深度70 km[15],其下为Maxwell粘弹性上地幔,粘滞性系数固定为1×1020 Pa·s。对于模型2,根据Nábělek等[16]的研究成果,设定印度俯冲板片在MFT以南厚度为50 km,而在MFT以北,随着向青藏高原下地壳俯冲,其厚度逐渐减小为25 km,印度板块和青藏高原上地幔的边界由俯冲板片下边界扩展划分得到,其他参数与模型1保持一致。通过上述方法可构建考虑喜马拉雅区域尼泊尔中部的横向不均匀性的岩石圈流变结构模型。
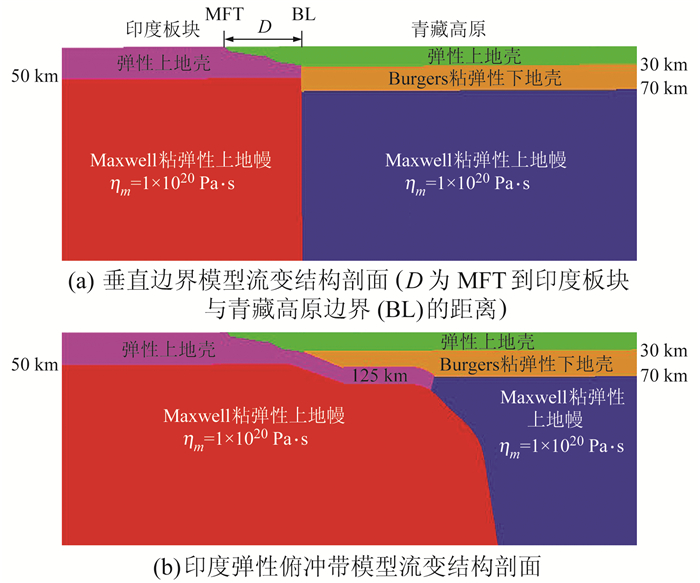
|
图 3 喜马拉雅区域尼泊尔中部的横向不均匀流变结构 Fig. 3 Lateral heterogeneous rheological structure across the central Nepal in Himalaya region |
采用Pylith有限元分析软件模拟尼泊尔地震震后粘弹性松弛效应[17],从而约束青藏高原南缘的流变参数。将Pylith中GenMaxwell体转换为双粘性Burgers体来表示青藏高原下地壳的流变属性[18],Burgers体可同时捕捉到震后早期形变的快速衰减和长期线性变化。本文定义稳态Maxwell粘滞系数ηm为瞬态Kelvin粘滞系数ηk的10倍[3]。考虑到主震和MW7.3最大余震的影响,为更可靠地模拟震后形变,本文基于“双断坡”断层模型重新反演主震和MW7.3余震的同震滑动。通过最邻近内插方法将同震滑动施加到断层面上以驱动粘弹性松弛的发生。岩石对粘弹性松弛效应的响应由区域流变结构决定,通过评估模拟值和观测值之间的加权均方根(WRMS)来搜索最优的流变参数,计算公式为:
| $ \chi^{2}=\sum\limits_{n=1}^{N} \sum\limits_{i=1}^{2} \sum\limits_{t=1}^{T} \frac{\left(\operatorname{obs}_{n, i, t}-c a l_{n, i, t}\right)^{2}}{\sigma_{n, i, t}^{2}} $ | (3) |
式中,N为GPS点数量; T为观测时间; obs和cal分别为观测值和模拟值; σ为GPS观测值的不确定度。
以往研究认为,尼泊尔地震的震后形变受多种机制影响(震后余滑、粘弹性松弛),而粘弹性松弛主要控制远场位移及整体震后形变的长期效应[3, 9]。因此,为更准确地探测青藏高原下地壳的粘滞系数,本文采用2种方案进行约束并相互验证:1)假设余滑在震后2 a内完全衰减[9],采用所有GPS站点震后2~5 a的观测数据进行约束;2)采用距同震破裂区200 km以外的9个远场GPS点(XZZB, XZAR、CANA、QIRE、YANI、J030、JZLS、J038、J338)震后5 a的观测数据进行拟合约束,由于远场点J337的观测位移比周围其他点偏大,从而使粘滞系数减小,因此计算时不采用该点数据。
3 结果分析 3.1 模型1结果采用模型1模拟粘弹性松弛并进行最优化分析,该过程中使用2个参数:青藏高原南缘下地壳的稳态Maxwell粘滞系数ηm(变化范围为1×1017~1×1019 Pa·s)以及MFT到印度板块与青藏高原板块垂直边界的距离D(变化范围为120~180 km)。为提高计算效率,首先设置较大的参数间隔进行搜索,然后在误差较小的范围内搜索最优的岩石圈流变参数。图 4(a)为采用所有GPS站点震后2~5 a的观测数据约束的最优参数D和ηm,图 4(b)为采用远场GPS站点震后5 a的数据约束的结果,2种方法约束的参数结果相等:D为130 km,ηm和ηk分别为3×1018 Pa·s和3×1017 Pa·s。图 4(c)为观测的GPS站点震后5 a累积位移(蓝色箭头)和模拟的地面节点累积位移(绿色箭头),图中颜色变化代表模拟的垂直位移。从图中可以看出,模拟结果整体显示为南-西南的水平地面运动模式,与观测数据基本一致,并且可以很好地解释远场点的观测位移,但中近场模拟的水平位移严重偏小,这可能是因为未考虑震后余滑的影响。
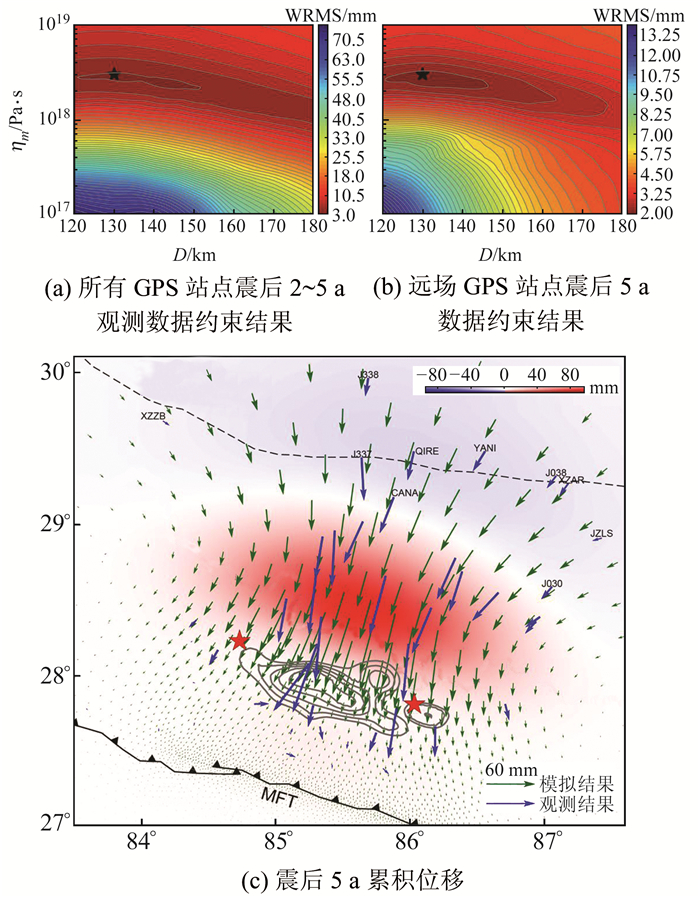
|
图 4 垂直边界模型的最优网格搜索结果和震后5 a累积位移 Fig. 4 The optimal grid search results and cumulative displacements of 5 years after the earthquake obtained by vertical boundary model |
对于模型2,由于印度板块与青藏高原板块的边界由印度俯冲板片的下边界来确定,因此只约束青藏高原下地壳稳态粘滞系数ηm。首先完成ηm变化范围在1×1017~1×1019 Pa·s之间的粘弹性松弛模拟,然后采用与§3.1相同的方法进行最优化网格搜索,2种方案的搜索结果如图 5(a)和5(b)所示。图 5(a)为采用所有GPS站点震后2~5 a的观测数据约束的结果,图 5(b)为采用远场GPS站点震后5 a的数据约束的结果,红色圆点代表最优参数,2种方法约束的青藏高原下地壳稳态粘滞系数均为1×1018 Pa·s,对应的瞬态粘滞系数为1×1017 Pa·s,比模型1约束的结果更小。图 5(c)为震后5 a的累积位移,蓝色箭头代表GPS观测位移,绿色箭头为模拟的地面格网节点位移,颜色变化代表模拟的垂直位移。从图中可以看出,其与观测数据和模型1具有非常接近的水平运动模式,可合理地解释远场GPS站点的水平观测位移,但中近场的模拟值远小于观测值。
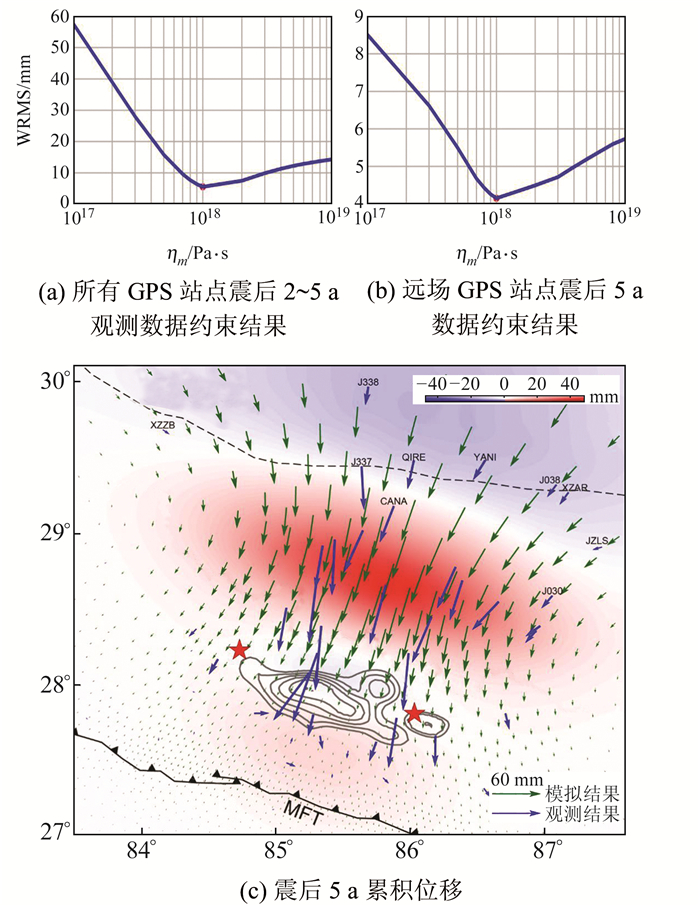
|
图 5 印度俯冲板片模型的最优网格搜索结果和震后5 a累积位移 Fig. 5 The optimal grid search results and cumulative displacements of 5 years after the earthquake obtained by India subduction slab model |
通过上述分析可知,2种边界模型均可产生南-西南水平方向运动模式,与观测的地面位移具有很好的一致性,但模型2约束的青藏高原下地壳粘滞系数略小于模型1,原因有2个方面:一是D和ηm之间的折中关系会导致印度板块与青藏高原板块的垂直边界更偏南,使得青藏高原下地壳向南延伸,范围变大;二是印度弹性俯冲板片向青藏高原下地壳推挤会降低粘弹性层的厚度。关于垂直形变(图 4(c)和5(c)中颜色变化),2种模型的模拟结果均显示了中尼边界附近及以北地区的隆升现象和雅鲁藏布江缝合带周围的沉降现象,但大小具有很大差异,模型1的垂直位移峰值约为80 mm,而模型2约为40 mm,模型2的垂直位移与GPS观测的垂直位移更为一致。而对于中尼边界以南的区域,粘弹性松弛模拟的垂直位移远小于观测值,这可能与其他机制有关(如震后余滑)。
模型1和模型2采用所有GPS站点震后2~5 a的水平位移拟合计算的WRMS分别为3.42 mm和6.78 mm,而采用远场点震后5 a的水平位移拟合计算的WRMS分别为2.13 mm和4.08 mm。相比之下,模型1的WRMS较模型2更小,虽然可以说明模型1能更好地解释观测的水平位移,但这主要是由于模型1中考虑了参数D和ηm之间的权衡问题。而事实上,由于印度板块俯冲碰撞欧亚板块的复杂性,仅以参数D来简化印度板块与青藏高原板块的边界位置并不合理。目前采用大地电磁、地震波层析成像及地质学等方法揭示的青藏高原南缘主前缘逆冲断裂带(MFT)、主中央逆冲断裂带(MCT)和主喜马拉雅逆冲断裂带(MHT)可为初步构建区域流变结构提供重大参考与约束。由于GPS垂直形变观测误差较大,影响因素较多,且模拟结果也难以完全解释垂直观测值,因此本文未计算其WRMS值,只能整体分析不同结果之间的差异。
如果只考虑粘弹性松弛机制的影响,则印度俯冲板片模型能更可靠地解释震后观测形变,尤其是垂直位移,且该模型也更接近其他方法(如接收函数法)推断的喜马拉雅-西藏碰撞带的地下岩石圈结构。总体来看,本文约束的青藏高原下地壳的稳态粘滞系数ηm约为(1~3)×1018 Pa·s,与前人的研究结果接近[8-9];但Zhao等[3]采用该地震震后1 a的形变数据约束得到的青藏高原南缘的粘滞系数更大,为8×1018 Pa·s,这是由于其考虑了更低粘滞系数的青藏高原上地幔,而本文仅固定其粘滞系数为1×1020 Pa·s。
4 结语本文基于尼泊尔及青藏高原南缘的GPS站点观测数据,采用有限元方法模拟分析2015年尼泊尔MW7.8地震震后5 a的粘弹性松弛效应,探测青藏高原南缘的岩石圈流变结构。采用Burgers体代表青藏高原下地壳的流变属性,并用2种不同的印度板块与青藏高原板块的边界结构(垂直边界结构和印度弹性俯冲板片结构)来构建模型。结果表明,2种结构均能很好地反映远场震后水平观测位移,并且约束的稳态粘滞系数较为接近,量级为1018,比瞬态Kelvin粘滞系数小1个数量级;但垂直形变差异较大,垂直边界结构的垂直位移严重偏离观测值,而采用俯冲板片结构模拟的垂直形变可以解释中尼边界及以北地区的震后隆升现象。后续研究可结合震后余滑机制进一步探测该区域的岩石圈流变特性。
| [1] |
赵斌. 利用震后GPS资料探测青藏高原东、南边界岩石圈流变结构[D]. 武汉: 武汉大学, 2017 (Zhao Bin. Probing the Rheological Structure across the Eastern and Southern Edges of the Tibetan Plateau Using GPS Observed Postseismic Displacements[D]. Wuhan: Wuhan University, 2017)
(  0) 0) |
| [2] |
Bürgmann R, Dresen G. Rheology of the Lower Crust and Upper Mantle: Evidence from Rock Mechanics, Geodesy, and Field Observations[J]. Annual Review of Earth and Planetary Sciences, 2008, 36(1): 531-567 DOI:10.1146/annurev.earth.36.031207.124326
(  0) 0) |
| [3] |
Zhao B, Bürgmann R, Wang D Z, et al. Dominant Controls of Downdip Afterslip and Viscous Relaxation on the Postseismic Displacements Following the MW7.9 Gorkha, Nepal, Earthquake[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(10): 8 376-8 401 DOI:10.1002/2017JB014366
(  0) 0) |
| [4] |
Huang M H, Bürgmann R, Freed A M. Probing the Lithospheric Rheology across the Eastern Margin of the Tibetan Plateau[J]. Earth and Planetary Science Letters, 2014, 396: 88-96 DOI:10.1016/j.epsl.2014.04.003
(  0) 0) |
| [5] |
Pollitz F, Banerjee P, Grijalva K, et al. Effect of 3-D Viscoelastic Structure on Post-Seismic Relaxation from the 2004 M=9.2 Sumatra Earthquake[J]. Geophysical Journal International, 2008, 173(1): 189-204 DOI:10.1111/j.1365-246X.2007.03666.x
(  0) 0) |
| [6] |
屈春燕, 左荣虎, 单新建, 等. 尼泊尔MW7.8地震InSAR同震形变场及断层滑动分布[J]. 地球物理学报, 2017, 60(1): 151-162 (Qu Chunyan, Zuo Ronghu, Shan Xinjian, et al. Coseismic Deformation Field of the Nepal MS8.1 Earthquake from Sentinel-1A/InSAR Data and Fault Slip Inversion[J]. Chinese Journal of Geophysics, 2017, 60(1): 151-162)
(  0) 0) |
| [7] |
Mendoza M M, Ghosh A, Karplus M S, et al. Duplex in the Main Himalayan Thrust Illuminated by Aftershocks of the 2015 MW7.8 Gorkha Earthquake[J]. Nature Geoscience, 2019, 12(12): 1 018-1 022 DOI:10.1038/s41561-019-0474-8
(  0) 0) |
| [8] |
Wang K, Fialko Y. Observations and Modeling of Coseismic and Postseismic Deformation Due to the 2015 MW7.8 Gorkha(Nepal) Earthquake[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(1): 761-779 DOI:10.1002/2017JB014620
(  0) 0) |
| [9] |
Tian Z, Freymueller J T, Yang Z Q. Spatio-Temporal Variations of Afterslip and Viscoelastic Relaxation Following the MW7.8 Gorkha(Nepal) Earthquake[J]. Earth and Planetary Science Letters, 2020, 532
(  0) 0) |
| [10] |
Unsworth M J, Jones A G, Wei W, et al. Crustal Rheology of the Himalaya and Southern Tibet Inferred from Magnetotelluric Data[J]. Nature, 2005, 438(7 064): 78-81
(  0) 0) |
| [11] |
Zeng J L, Zhang Z, Rollins C, et al. Postseismic Deformation Following the 2015 MW7.8 Gorkha(Nepal) Earthquake: New GPS Data, Kinematic and Dynamic Models, and the Roles of Afterslip and Viscoelastic Relaxation[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(9)
(  0) 0) |
| [12] |
赵斌, 王东振, 谭凯, 等. 顾及粘弹性松弛效应的2015年尼泊尔MW7.9地震震后早期余滑模型[J]. 大地测量与地球动力学, 2018, 38(3): 239-243 (Zhao Bin, Wang Dongzhen, Tan Kai, et al. Afterslip Model Following the 2015 Nepal MW7.9 Earthquake Considering Viscoelastic Relaxation Displacements[J]. Journal of Geodesy and Geodynamics, 2018, 38(3): 239-243)
(  0) 0) |
| [13] |
Elliott J R, Jolivet R, González P J, et al. Himalayan Megathrust Geometry and Relation to Topography Revealed by the Gorkha Earthquake[J]. Nature Geoscience, 2016, 9(2): 174-180 DOI:10.1038/ngeo2623
(  0) 0) |
| [14] |
Monsalve G, Sheehan A, Schulte-Pelkum V, et al. Seismicity and One-Dimensional Velocity Structure of the Himalayan Collision Zone: Earthquakes in the Crust and Upper Mantle[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B10)
(  0) 0) |
| [15] |
Kind R, Yuan X H, Sual J, et al. Seismic Images of Crust and Upper Mantle beneath Tibet: Evidence for Eurasian Plate Subduction[J]. Science, 2002, 298(5 596): 1 219-1 221
(  0) 0) |
| [16] |
Nábělek J, Hetényi G, Vergne J, et al. Underplating in the Himalaya-Tibet Collision Zone Revealed by the Hi-CLIMB Experiment[J]. Science, 2009, 325(5 946): 1 371-1 374
(  0) 0) |
| [17] |
Aagaard B T, Knepley M G, Williams C A. A Domain Decomposition Approach to Implementing Fault Slip in Finite-Element Models of Quasi-Static and Dynamic Crustal Deformation[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(6): 3 059-3 079 DOI:10.1002/jgrb.50217
(  0) 0) |
| [18] |
Müller G. Generalized Maxwell Bodies and Estimates of Mantle Viscosity[J]. Geophysical Journal International, 1986, 87(3): 1 113-1 141 DOI:10.1111/j.1365-246X.1986.tb01986.x
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


