2. 中国科学院大学,北京市玉泉路19号甲,100049
对TDOA定位模式下的LOS信号场景的算法研究很多[1-14],包括两步加权最小二乘(two-step weighted least squares,TSWLS)算法[1]、线性修正最小二乘(linear-correction least-squares,LCLS)算法[2]、约束加权最小二乘(constrained weighted least squares,CWLS)算法[3-4]、分离约束加权最小二乘(separated CWLS,SCWLS)算法[5]和迭代约束加权最小二乘(iterative CWLS,ICWLS)算法[6]等。但这些方法难以同时兼顾精度和抗噪性能。为此,本文提出一种简单有效的非约束迭代优化算法,并用实验验证其效果。
1 算法描述结合室内定位的特点,考虑采用N个UWB基准站去定位UWB标签的2维坐标。假设s i=[xi, yi]T为已知UWB基站坐标,u0=[x, y]T为待求标签位置,通常选择第1个基站作为参考站,则常规TDOA-LOS定位方程为:
| $ \begin{gathered} d_{i, 1}=\sqrt{\left(x-x_{i}\right)^{2}+\left(y-y_{i}\right)^{2}}- \\ \sqrt{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}+\eta_{i} \end{gathered} $ | (1) |
式中,di, 1为标签到第i个基站和到第1个基站之间的距离差,ηi为均值为0的高斯白噪声。对式(1)移项后进行平方展开,忽略高斯白噪声的影响,可将其转化为线性形式Gu1= h,其中,
| $ \boldsymbol{G}=\left[\begin{array}{ccc} x_{2}-x_{1} & y_{2}-y_{1} & d_{2,1} \\ x_{3}-x_{1} & y_{3}-y_{1} & d_{3,1} \\ \vdots & \vdots & \vdots \\ x_{N}-x_{1} & y_{N}-y_{1} & d_{N, 1} \end{array}\right] $ | (2) |
| $ \boldsymbol{u}_{1}=[x, y, R]^{\mathrm{T}} $ | (3) |
| $ \boldsymbol{h}=\frac{1}{2}\left[R_{2}^{2}-R_{1}^{2}-d_{2,1}^{2} \quad \cdots \quad R_{N}^{2}-R_{1}^{2}-d_{N, 1}^{2}\right]^{\mathrm{T}} $ | (4) |
式中,
由于R与u0和s1之间存在如下关系:
| $ R^{2}=\left(\boldsymbol{u}_{0}-\boldsymbol{s}_{1}\right)^{\mathrm{T}}\left(\boldsymbol{u}_{0}-\boldsymbol{s}_{1}\right) $ | (5) |
| $ \begin{aligned} &\min \left(\boldsymbol{h}-\boldsymbol{G} \boldsymbol{u}_{1}\right)^{\mathrm{T}} \boldsymbol{W}\left(\boldsymbol{h}-\boldsymbol{G} \boldsymbol{u}_{1}\right) \\ &\mathrm{s} . \mathrm{t} . \quad R^{2}=\left(\boldsymbol{u}_{0}-\boldsymbol{s}_{1}\right)^{\mathrm{T}}\left(\boldsymbol{u}_{0}-\boldsymbol{s}_{1}\right) \end{aligned} $ | (6) |
式中,W为加权矩阵。
CWLS算法已有较为快速的解法,但在定位精度方面仍存在较大的提升空间。为进一步提高CWLS算法的定位精度和运算速度,并解决约束方程的非凸问题,Qu等[6]提出迭代约束加权最小二乘(ICWLS)算法。该算法通过新的等式变换,将具有非凸特性的CWLS算法表达式转化成具有凸性的新表达式。尽管仿真实验证实了该算法的有效性,但在大噪声环境下却存在定位发散的缺点。
为解决定位发散的问题,本文提出一种简单且适用于大噪声环境下的TDOA定位算法。首先假设基准站坐标位于笛卡尔坐标系原点(即便真实场景中基准站坐标不在原点,也可通过坐标变换来实现),因此,式(1)可被重新写为:
| $ d_{i, 1}=\sqrt{\left(x-x_{i}\right)^{2}+\left(y-y_{i}\right)^{2}}-\sqrt{x^{2}+y^{2}}+\eta_{i} $ | (7) |
通常在室内环境中,观测值不会很大且白噪声较小,而白噪声的分析常用于计算加权矩阵,由于本文算法不属于加权类算法,因此可忽略式(7)中噪声项的影响。利用勾股定理,可将式(7)转化为:
| $ \left(d_{i, 1}+R\right)^{2}=\left(x-x_{i}\right)^{2}+\left(y-y_{i}\right)^{2} $ | (8) |
展开移项后可得到:
| $ 2 d_{i, 1} R=x_{i}^{2}+y_{i}^{2}-d_{i, 1}^{2}-2 x_{i} x-2 y_{i} y $ | (9) |
令
| $ \boldsymbol{A}=\left[\begin{array}{ccc} d_{2,1} & \cdots & d_{N, 1} \end{array}\right]^{\mathrm{T}} $ | (10) |
| $ \boldsymbol{C}= {\left[\begin{array}{c} x_{2}^{2}+y_{2}^{2}-d_{2,1}^{2} \\ \vdots \\ x_{N}^{2}+y_{N}^{2}-d_{N, 1}^{2} \end{array}\right]} $ | (11) |
| $ \boldsymbol{B}=\left[\begin{array}{cc} x_{2} & y_{2} \\ \vdots & \vdots \\ x_{N} & y_{N} \end{array}\right] $ | (12) |
则式(9)可写为如下线性形式:
| $ 2 \boldsymbol{A} R=\boldsymbol{C}-2 \boldsymbol{B} \boldsymbol{X}_{*} $ | (13) |
式中,X*= [x y ]T为标签坐标。由于R和X*之间存在关系式
| $ \boldsymbol{B} \boldsymbol{X}_{*}=\frac{1}{2}\left(\boldsymbol{C}-2 \boldsymbol{A} \sqrt{\boldsymbol{X}_{*}^{\mathrm{T}} \boldsymbol{X}_{*}}\right) $ | (14) |
对于式(14),由于左右两边均含有未知的变量X*,故需要事先提供一个定位坐标初值X *(k),然后将其代入式(14)右边,将其转化为只含1个未知数的表达式,最后采用迭代解算策略,得到新的定位结果X*(k+1):
| $ \boldsymbol{X}_{*}^{(k+1)}=\frac{1}{2}\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}}\left(\boldsymbol{C}-2 \boldsymbol{A} \sqrt{\left(\boldsymbol{X}_{*}^{(k)}\right)^{\mathrm{T}} \boldsymbol{X}_{*}^{(k)}}\right) $ | (15) |
当式(15)多次迭代后达到式(16)的迭代停止准则时,即可停止迭代,从而输出最终定位结果:
| $ \sqrt{\left(\boldsymbol{X}^{(k+1)}-\boldsymbol{X}^{(k)}\right)^{\mathrm{T}}\left(\boldsymbol{X}^{(k+1)}-\boldsymbol{X}^{(k)}\right)} \leqslant \varepsilon $ | (16) |
式中,ε为误差阈值,数值一般比较小。
此外,计算X*(k+1)的期望可以得到:
| $ \begin{aligned} &E\left(\boldsymbol{X}_{*}^{(k+1)}\right)=\\ &E\left(\frac{1}{2}\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}}\left(\boldsymbol{C}-2 \boldsymbol{A} \sqrt{\left(\boldsymbol{X}_{*}^{(k)}\right)^{\mathrm{T}} \boldsymbol{X}_{*}^{(k)}}\right)\right)=\\ &E\left(\frac{1}{2}\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}}(\boldsymbol{C}-2 \boldsymbol{A} R)\right)=\\ &E\left(\frac{1}{2}\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}}\left(2 \boldsymbol{B} \boldsymbol{X}_{*}^{(k)}\right)\right)=\\ &\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{B} \cdot E\left(\boldsymbol{X}_{*}^{(k)}\right)=E\left(\boldsymbol{X}_{*}^{(k)}\right) \end{aligned} $ | (17) |
通常初值可以由最小二乘算法得到,而最小二乘解是无偏的,因此式(17)中每步迭代解的期望都等于最小二乘解,是无偏估计解。
2 仿真实验通常情况下,室内环境相对复杂,视距条件下的基站总数相对有限。为保证UWB定位算法的可行性,仅采用4个UWB基站定位标签的位置,坐标分别为A1(0, 0)、A2(10, 0)、A3(10, 10)和A4(0, 10),标签接收来自各个基站的信号中含有均值为0、方差为σ2的高斯白噪声ηi。由于本文的主要目的是评价算法在大噪声环境下的性能,故将噪声方差分别设置为0.1、0.25、0.5、0.75和1以进行综合评价,将每个噪声方差下的蒙特卡洛仿真实验次数和迭代阈值ε分别设置为2 000和0.000 01。
基于Qu等[6]的仿真实验结论可知,ICWLS算法的定位精度优于TSWLS算法、SDR算法、CWLS算法和迭代似然估计法,因此本文仅选择该算法与本文算法进行对比。在定位初值方面,2种算法均采用最小二乘解作为迭代初值;在精度评价指标方面,本文采用均方根误差(RMSE)来评估2种算法的性能,计算公式为:
| $ \mathrm{RMSE}=\frac{1}{2\ 000} \sum\limits_{i=1}^{2\ 000} \sqrt{\left(\boldsymbol{X}_{i^{*}}-\tilde{\boldsymbol{X}}_{i}\right)^{\mathrm{T}}\left(\boldsymbol{X}_{i^{*}}-\tilde{\boldsymbol{X}}_{i}\right)}。$ |
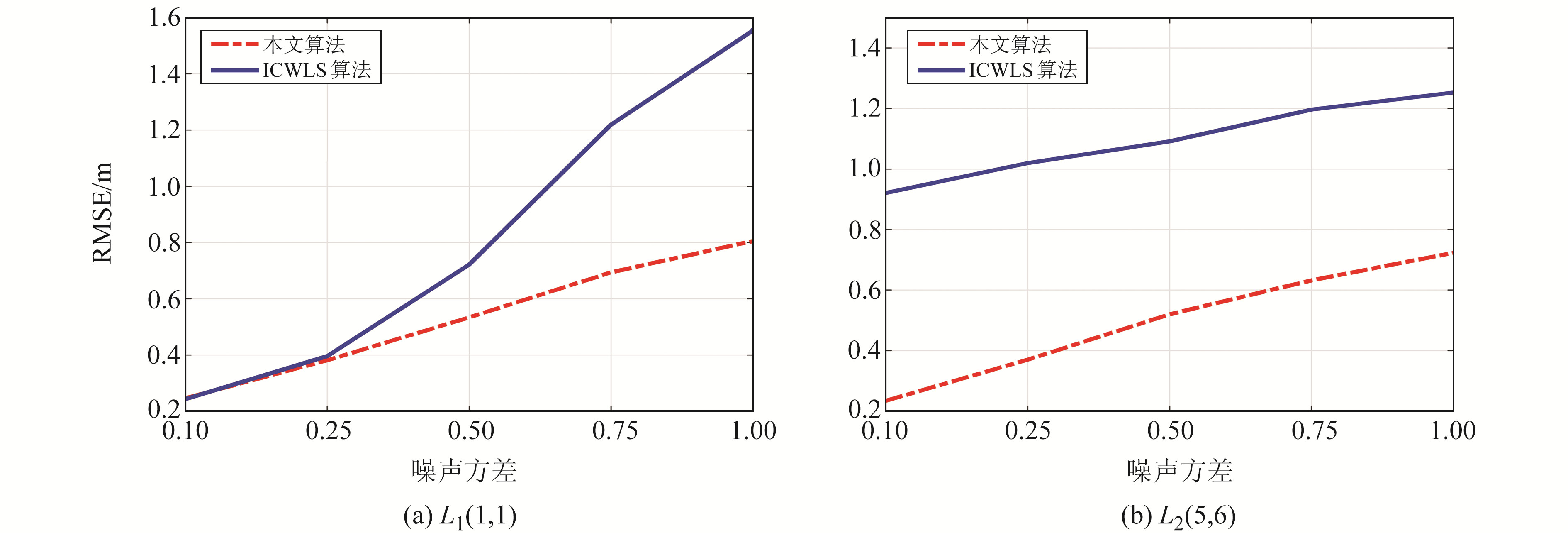
为充分对比2种算法在边缘点和中心点处的定位精度,在LOS信号环境下选择近基站点L1(1, 1)和近中心点L2(5, 6)进行测试,2种算法在测试点处的定位精度见图 1。由图可知,当噪声方差σ2≤0.25时,ICWLS算法的精度性能与本文算法大致相同。然而,当σ2>0.25时,ICWLS算法的性能误差开始急剧上升,而本文算法则缓慢上升,且误差低于ICWLS算法。因此,总体而言,本文算法在定位精度和抗噪声性能方面表现更好。
|
图 1 2种算法在不同点处的定位精度 Fig. 1 RMSE of two methods at different points |
为进一步测试2种算法的定位精度,在4个基站围成的矩形区域中随机生成标签的位置,实验结果见图 2。可以看出,本文算法显著优于ICWLS算法,在数值方面,本文算法的相应误差大约只有ICWLS算法的一半。此外,实验发现,本文算法迭代到收敛的平均迭代次数为15次。

|
图 2 2种算法在随机点环境下的定位精度 Fig. 2 RMSE of two methods at random point |
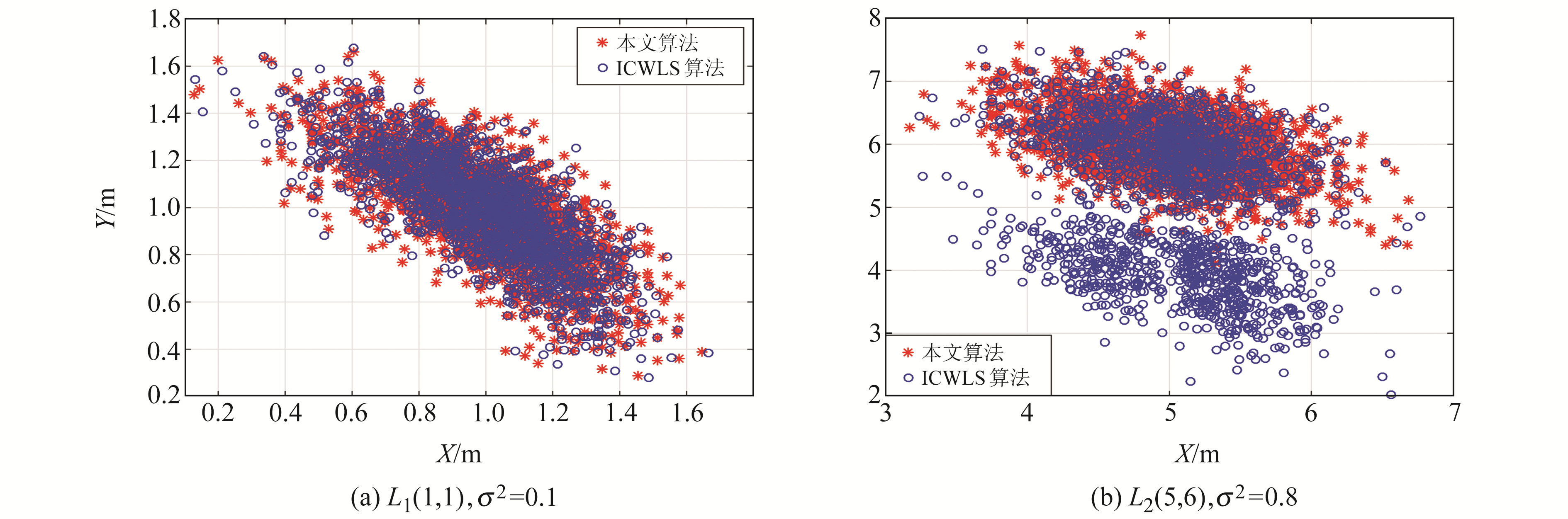
基于实验1和实验2的仿真结果,通过定位散点图来探究ICWLS算法定位性能较差的原因。将标签位置分别固定在L1(1, 1)和L2(5, 6)处,并将其噪声方差分别设为低噪声σ2=0.1和高噪声σ2=0.8,结果见图 3。从图中可以看出,在低噪声条件下,2种算法的定位坐标基本分布在同一区域内,变化不大;在高噪声条件下,本文算法的定位结果接近真值,但ICWLS算法的定位结果分布在2个不同的区域,产生严重的发散。结合2种实验场景的定位结果认为,ICWLS算法存在一定的发散现象,这种发散现象在低噪声环境下不明显,在高噪声环境下相对明显,而本文提出的定位算法具有良好的收敛性和抗噪声性能。
|
图 3 2种算法在不同点处的定位坐标 Fig. 3 Coordinates of two methods at different points |
由此认为:1)本文提出的算法优于ICWLS算法;2)无论噪声方差是多少,本文算法的定位结果都与真实位置更接近,说明本文算法具有良好的抗噪声性能;3)ICWLS算法存在定位发散的缺点,这可能是其定位性能不如本文算法的根本原因。
3 结语针对传统TDOA算法因抗噪性能弱而导致定位发散的缺点,本文提出一种简单的TDOA定位算法。该算法首先将TDOA定位方程转化为LS形式来得到初始解,然后通过迭代思想得到收敛坐标。本文算法原理简单、抗噪声性能好、易于实现,可推广到工业领域,且仿真结果也验证了本文算法具有可行性和有效性,定位精度优于ICWLS算法。
| [1] |
Chan Y T, Ho K C. A Simple and Efficient Estimator for Hyperbolic Location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905-1915 DOI:10.1109/78.301830
(  0) 0) |
| [2] |
Huang Y T, Benesty J, Elko G W, et al. Real-Time Passive Source Localization: A Practical Linear-Correction Least-Squares Approach[J]. IEEE Transactions on Speech and Audio Processing, 2001, 9(8): 943-956 DOI:10.1109/89.966097
(  0) 0) |
| [3] |
Yu H G, Huang G M, Gao J, et al. An Efficient Constrained Weighted Least Squares Algorithm for Moving Source Location Using TDOA and FDOA Measurements[J]. IEEE Transactions on Wireless Communications, 2012, 11(1): 44-47 DOI:10.1109/TWC.2011.102611.110728
(  0) 0) |
| [4] |
Quo F C, Ho K C. A Quadratic Constraint Solution Method for TDOA and FDOA Localization[C]. IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), Prague, 2011
(  0) 0) |
| [5] |
Lin L X, So H C, Chan F K W, et al. A New Constrained Weighted Least Squares Algorithm for TDOA-Based Localization[J]. Signal Processing, 2013, 93(11): 2872-2878 DOI:10.1016/j.sigpro.2013.04.004
(  0) 0) |
| [6] |
Qu X M, Xie L H, Tan W R. Iterative Constrained Weighted Least Squares Source Localization Using TDOA and FDOA Measurements[J]. IEEE Transactions on Signal Processing, 2017, 65(15): 3990-4003 DOI:10.1109/TSP.2017.2703667
(  0) 0) |
| [7] |
Li J Z, Guo F C, Yang L, et al. On the Use of Calibration Sensors in Source Localization Using TDOA and FDOA Measurements[J]. Digital Signal Processing, 2014, 27: 33-43 DOI:10.1016/j.dsp.2013.12.011
(  0) 0) |
| [8] |
Qiao T Z, Zhang Y, Liu H P. Nonlinear Expectation Maximization Estimator for TDOA Localization[J]. IEEE Wireless Communications Letters, 2014, 3(6): 637-640 DOI:10.1109/LWC.2014.2364023
(  0) 0) |
| [9] |
Jia T Y, Wang H Y, Shen X H, et al. Target Localization Based on Structured Total Least Squares with Hybrid TDOA-AOA Measurements[J]. Signal Processing, 2018, 143: 211-221 DOI:10.1016/j.sigpro.2017.09.011
(  0) 0) |
| [10] |
Qu X M, Xie L H. An Efficient Convex Constrained Weighted Least Squares Source Localization Algorithm Based on TDOA Measurements[J]. Signal Processing, 2016, 119: 142-152 DOI:10.1016/j.sigpro.2015.08.001
(  0) 0) |
| [11] |
Xu B, Qi W D, Wei L, et al. Turbo-TSWLS: Enhanced Two-Step Weighted Least Squares Estimator for TDOA-Based Localization[J]. Electronics Letters, 2012, 48(25): 1597-1598 DOI:10.1049/el.2012.2848
(  0) 0) |
| [12] |
Zou Y B, Liu H P, Wan Q. An Iterative Method for Moving Target Localization Using TDOA and FDOA Measurements[J]. IEEE Access, 2018, 6: 2746-2574 DOI:10.1109/ACCESS.2017.2785182
(  0) 0) |
| [13] |
Wang G, Li Y M, Ansari N. A Semidefinite Relaxation Method for Source Localization Using TDOA and FDOA Measurements[J]. IEEE Transactions on Vehicular Technology, 2013, 62(2): 853-862 DOI:10.1109/TVT.2012.2225074
(  0) 0) |
| [14] |
Noroozi A, Oveis A H, Hosseini S M, et al. Improved Algebraic Solution for Source Localization from TDOA and FDOA Measurements[J]. IEEE Wireless Communications Letters, 2018, 7(3): 352-355 DOI:10.1109/LWC.2017.2777995
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2021, Vol. 41
2021, Vol. 41

