由于GEO卫星的高轨道特性以及静地几何特征,其轨道的确定和预报难度较大,卫星轨道精度较低。但同时其拥有更高的区域可见性,能有效增加卫星数,进一步提高区域导航性能。研究表明,目前BDS的GEO卫星的精密定轨精度为dm级[1-5]。许多学者对GEO卫星位置计算、广播星历误差、卫星钟差、BDS服务性能以及定位精度进行了研究,然而对GEO卫星的引入对BDS高精度定位性能的改善的详细分析较少,特别是在BDS高精度相对定位方面。因此,本文基于非差观测模型推导BDS长距离相对定位模型,利用长距离基线估计测站位置坐标、整周模糊度和对流层延迟误差参数; 通过MGEX测站BDS观测数据,设计BDS IGSO+MEO组合星座以及BDS全星座相对定位的静态与动态对比实验; 同时,对GEO卫星的精密轨道精度进行研究,重点分析GEO卫星对BDS高精度长距离相对定位性能的影响。
1 BDS基本观测模型 1.1 BDS非差观测模型非差伪距观测值和载波相位观测值是BDS最基本的观测值,BDS相对定位采用多频伪距和载波相位非差观测值[6],其观测方程为:
| $ \begin{array}{l} {\lambda _i} \cdot \mathit{\Phi }_i^s = {{\boldsymbol{H}}^s} \cdot \delta {\boldsymbol{X}} + \rho _0^s - {\lambda _i} \cdot N_i^s - I_i^s + \\ \;\;\;\;\;\;\;\;\;\;\;{T^s} + {O^s} + {t_R} - {t^s} + \varepsilon _i^s \end{array} $ | (1) |
| $ P_i^s = {{\boldsymbol{H}}^s} \cdot \delta {\boldsymbol{X}} + \rho _0^s + I_i^s + {T^s} + {O^s} + {t_R} - {t^s} + \varepsilon _{ic}^s $ | (2) |
式中,Φ为载波相位观测值; P为伪距观测值; ρ0为测站到卫星间的几何距离; λ为载波相位波长; N为载波相位整周模糊度; 下标i为频率; I为电离层延迟误差; T为对流层延迟误差; ts为卫星钟差; tR为接收机钟差; O为卫星轨道误差; δX为坐标初值改正量,即位置参数; H为未知参数的系数向量; 上标s为卫星号; ε为观测噪声。
1.2 随机模型BDS相对定位中,多项误差对观测值的影响与高度角有关[7]。本文根据卫星高度角大小来确定观测值的权重,采用基于高度角的随机模型:
| $ {\sigma ^2} = \left\{ \begin{array}{l} {a^2}, E \ge 30^\circ \\ 2{\sin ^2}E, 10^\circ < E < 30^\circ \end{array} \right. $ | (3) |
式中,σ为观测值噪声; a为因子; E为卫星高度角。
根据卫星高度角进行定权,其权值可表示为:
| $ P\left( E \right) = \left\{ \begin{array}{l} 1.0, E \ge 30^\circ \\ 2\sin E, 10^\circ < E < 30^\circ \end{array} \right. $ | (4) |
通过BDS非差观测方程获得相对定位模型。首先固定一个测站R为参考站,其非差载波相位观测方程为[8]:
| $ L_{iR}^s = \rho _R^s - {\lambda _i}N_{iR}^p + {t_R} - {t^s} - I_R^s + T_R^s + \varepsilon _{iR}^s $ | (5) |
参考站R载波相位观测值的非差误差改正数coriRs可表示为:
| $ \begin{array}{l} {\rm{cor}}_{iR}^s = L_{iR}^s - \rho _R^s = - {\lambda _i}N_{iR}^s + {t_R} - \\ \;\;\;\;\;\;\;\;\;\;{t^s} - I_{iR}^s + T_R^s + \varepsilon _{iR}^s \end{array} $ | (6) |
用户站U经过误差改正数coriRs改正后的观测方程为:
| $ \begin{array}{l} L_{iU}^s - {\rm{cor}}_{iR}^s = {\boldsymbol{H}}_U^s\delta {\boldsymbol{X}} + \rho _{oU}^s - \\ \;\;\;\;{\lambda _i}N_{iR}^s + t - \delta {I^s} + \delta {T^s} \end{array} $ | (7) |
式中各符号与式(1)和式(2)相同; δT和δI分别为对流层误差和电离层误差的残差; t=tU-tR; 将2个接收机钟差合并进行参数估计,参考站模糊度包含在模糊度参数NiURs中,下标R和U表示测站。同理可得到误差改正后的伪距观测方程,如果参考站与用户站的距离较短,则残差δIs和δTs较小,不影响载波相位整周模糊度的确定,未知参数和载波相位模糊度参数解算时可不考虑残差的影响。由此得到用户站其他卫星经过误差改正数改正后的观测方程,进而根据高度角相关的随机模型求解未知参数。最后确定载波相位整周模糊度浮点解和方差-协方差矩阵,使用LAMBDA方法搜索并确定载波相位整周模糊度,并对相对定位位置进行解算。
2.2 残余误差的处理对于式(7),考虑到电离层延迟误差以及对流层延迟误差随基线长度的增加会存在残余影响,因此将对流层延迟误差用单颗卫星和测站天顶对流层延迟误差的对流层投影函数表示。对流层投影函数可用与卫星高度角E有关的函数map表示:
| $ {\rm{map = }}\frac{{1.001}}{{\sqrt {0.002001 + {\rm{si}}{{\rm{n}}^2}E} }} $ | (8) |
天顶对流层延迟误差参数估计可采用分段线性函数。基线两端测站的共视卫星高度角相差很小,由于GEO和IGSO卫星的高轨道特性,基线两端测站同一卫星的高度角相差更小,投影函数差值也较小。考虑到式(8)计算得到的2个测站的投影函数数值相近,因此对其进行合并估计。对于中长距离基线,对流层延迟误差的残差为:
| $ \delta {T^s} = {\rm{ma}}{{\rm{p}}^s} \cdot {\rm{RZTD}} $ | (9) |
式中,RZTD为基线两端测站的相对天顶对流层延迟误差参数。电离层延迟误差残差的处理可采用参数估计的方式进行改正,电离层延迟误差可作为参数来估计,历元间电离层延迟误差参数变化可采用随机游走过程进行约束。
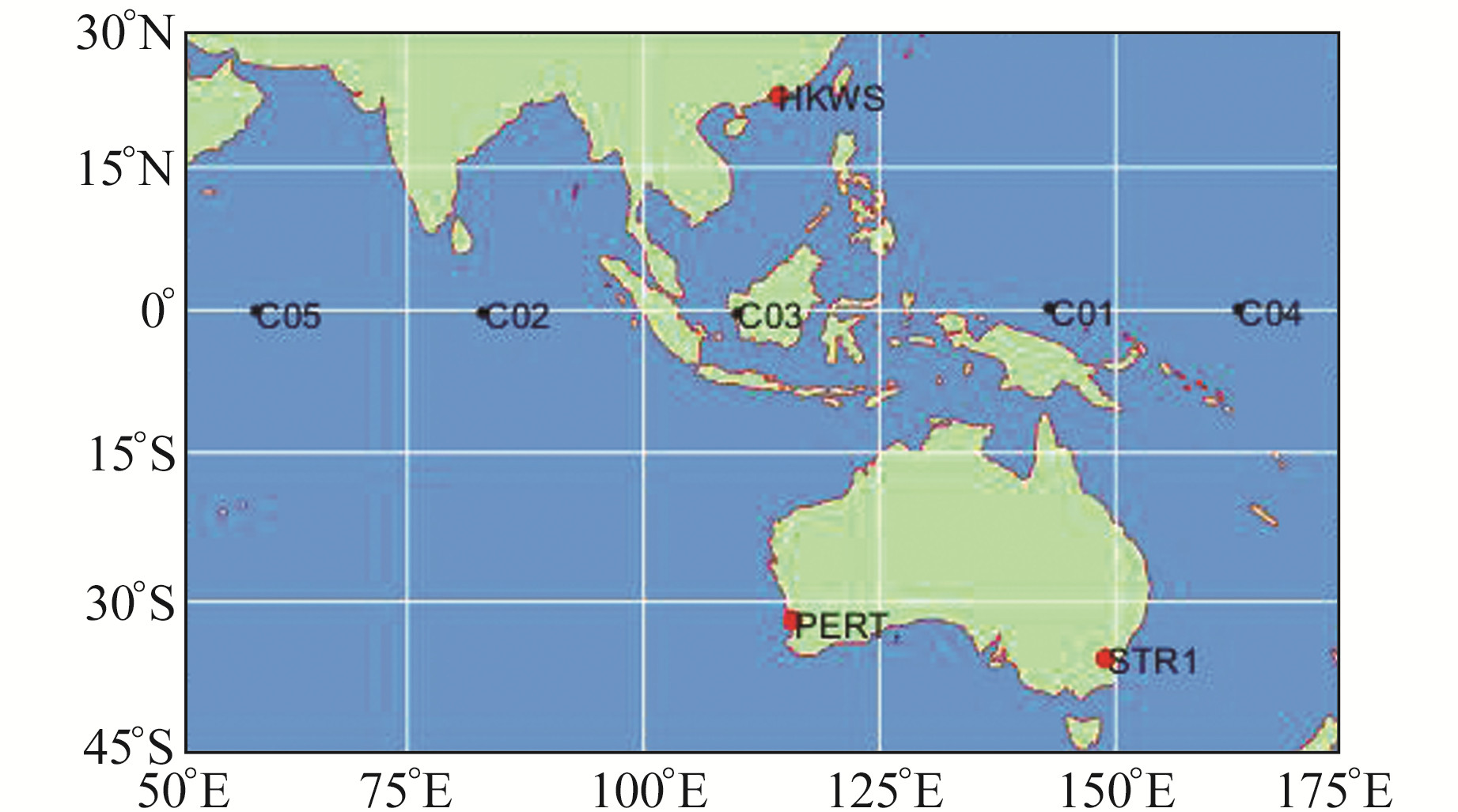
3 实验与结果分析采用香港、澳大利亚地区MGEX测站中的3组基线观测数据,观测时间为2018年doy050~075,详细情况见表 1。分别以STR1、HKWS、PERT站为基准站,对3组实验数据进行静态和动态BDS高精度相对定位实验,测站位置以及GEO卫星分布见图 1。以GFZ精密星历产品为参考验证BDS卫星精密轨道精度,以SLR数据作为参考值,根据GEO/IGSO/MEO卫星轨道的径向误差进行分析。选取GEO卫星C01、IGSO卫星C08和C10、MEO卫星C11进行统计分析,4颗卫星径向误差的STD和RMS值见表 2。
|
|
表 1 实验数据 Tab. 1 The experimental data |
|
图 1 测站分布 Fig. 1 Distribution of the stations |
|
|
表 2 径向误差的RMS和STD比较 Tab. 2 Comparison of RMS and STD of radial errors |
由表 2可知,GEO卫星轨道精度明显低于IGSO和MEO卫星。但GEO卫星在特定地区可被长期稳定地观测到,能够增加BDS卫星星座的可用卫星数量,改善卫星观测条件,增强观测模型的几何构型。在数据解算过程中,可通过采用降低GEO卫星观测值权重的方法降低GEO卫星的影响。
3.1 静态相对定位结果分析利用不同地区3条基线的观测数据分析GEO卫星对BDS静态相对定位的影响,以IGS周解的测站坐标作为参考值,采用2种BDS静态相对定位实验方案:方案1采用IGSO+MEO组合,方案2采用IGSO+MEO+GEO全星座组合。3组测站在各观测时段均包含3颗以上GEO卫星的观测数据。
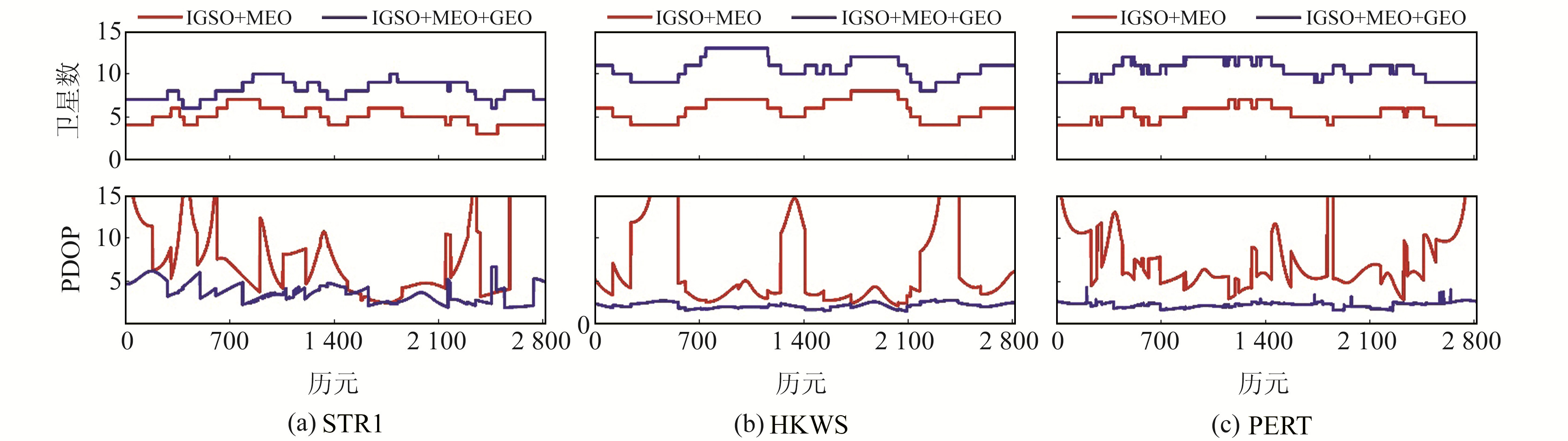
以doy056为例分析3个基准站可见卫星数和PDOP值,结果见图 2。可以看出,加入GEO卫星后,在卫星数较少时,GEO卫星能够显著改善几何构型,对加快解算收敛速度和提高定位精度有提升作用。
|
图 2 可见卫星数量和PDOP值 Fig. 2 The visible satellite numbers and PDOP values |
图 3为方案1和方案2静态相对定位单天解,定位结果统计信息见表 3。

|
图 3 静态基线单天解偏差 Fig. 3 The bias of single day solution of static baselines |
|
|
表 3 静态基线精度统计 Tab. 3 Statistics of static baselines accuracy |
可以看出,方案2各方向静态基线单天解精度均优于方案1。2种方案各测站平面精度均优于0.01 m,达到mm级; U方向上,2种方案均优于0.03 m。但因为单天24 h的观测数据时间较长,不使用GEO卫星的MEO+IGSO组合的定位精度相对于全星座差别较小。
将24 h分为12个观测时段,每段2 h,以doy056为例进行静态基线解算,定位结果见图 4,统计结果见表 4。

|
图 4 2 h静态基线误差对比 Fig. 4 Comparison of static baselines errors with 2 h |
|
|
表 4 2 h静态基线精度统计 Tab. 4 Statistics of static baselines accuracy with 2 h |
可以看出,加入GEO卫星对静态相对单天解和2 h解中U方向精度提升最为明显,E、N方向也有不同幅度提升。观测时长越短,GEO卫星对静态相对定位性能的提升越显著。相对定位模型对卫星轨道误差具有一定削弱作用,因此GEO卫星的轨道精度对相对定位,特别是中短基线的影响较小。
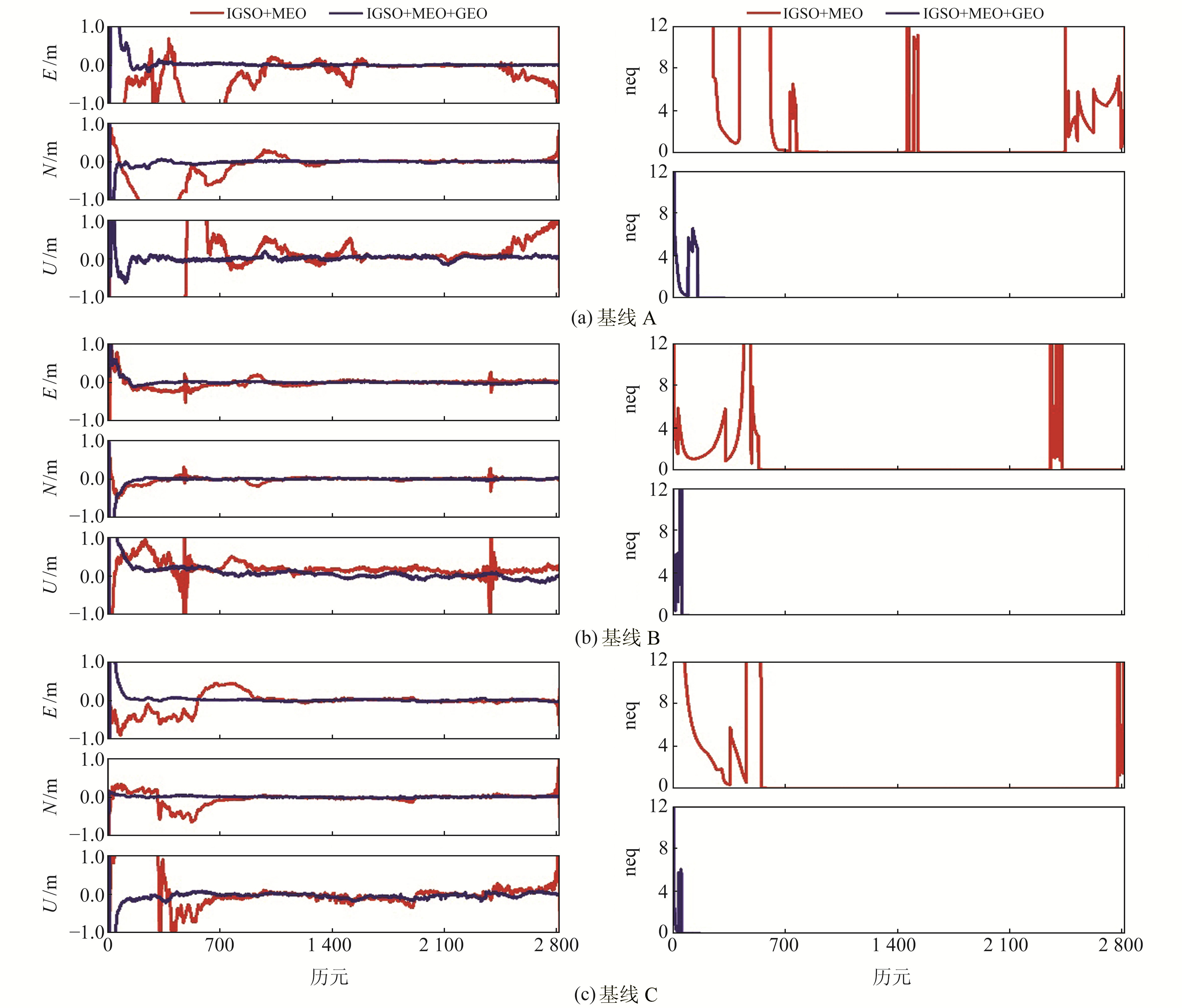
3.2 动态相对定位结果分析为了更准确地对模拟实时动态基线解算结果的收敛时间进行分析,以实时动态方式处理3条基线doy056的数据,定位结果见图 5(图中neq为法方程协因数主对角线上3个元素的矢量和)。可以看出,2种组合的法方程差异较大,加入GEO卫星后能有效改善卫星几何构型,提高定位精度。以doy056为例,对动态相对定位收敛后精度进行统计,统计结果见表 5。
|
图 5 动态基线误差比较 Fig. 5 Comparison of dynamic baselines errors |
|
|
表 5 动态相对定位精度统计 Tab. 5 Statistics of dynamic relative positioning accuracy |
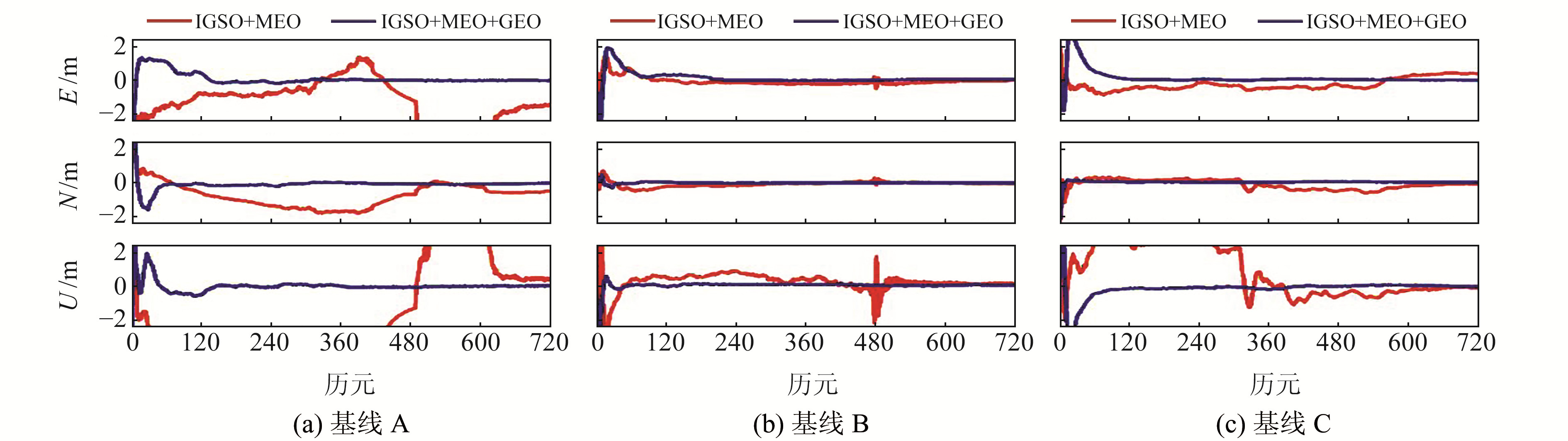
从图 5和表 5可以看出,加入GEO卫星后,3条基线动态解算结果均有大幅提升。图 6为doy056第1时段BDS动态相对定位偏差。对3个方向的误差进行RMS统计得到收敛时间,统计结果见表 6(单位min)。从表中可以看出,GEO卫星能显著提升BDS实时动态相对定位的定位性能,其中基线C在方案1动态模式下不收敛,方案2中,3个方向在60 min左右就可收敛到0.1 m以内,动态相对定位的结果和收敛速度大幅提升。
|
图 6 第1时段BDS动态相对定位偏差 Fig. 6 BDS dynamic relative positioning bias in period 1 |
|
|
表 6 收敛时间统计 Tab. 6 Statistics of convergence time |
基于高精度相对定位方法,利用静态和动态2种数据处理模式对包含GEO卫星的BDS全星座模式和不包含GEO卫星数据处理模式的2种实验方案的定位精度、PDOP值、收敛速度以及法方程等方面进行性能分析。结果表明,BDS全星座的卫星个数较多,各测站定位结果、PDOP值和几何构型均较为稳定; 不包含GEO卫星的数据处理中,观测时长较短或动态定位时,定位结果以及PDOP值起伏较大,平面精度优于U方向,N方向精度最高。静态相对定位单天解和2 h解中,缺失GEO卫星的定位精度低于全星座,其中2 h解算结果更为明显。缺少GEO卫星的动态定位相对于全星座的定位性能降低明显。虽然GEO卫星的轨道径向误差相对于IGSO和MEO卫星较大,但卫星数量和观测值的增加可明显提升定位性能,特别是卫星数较少的时段和动态定位数据处理模式,在较短的观测时间内可显著提升定位效果。而且相对定位中,通过差分组合降低了卫星轨道误差的影响,GEO卫星轨道径向误差大的缺陷可以通过相对定位的方式克服。
| [1] |
尹斌权, 岳东杰, 陈健, 等. 北斗GEO卫星多路径特性在SPP中的应用[J]. 地理空间信息, 2019, 17(3): 31-34 (Yin Binquan, Yue Dongjie, Chen Jian, et al. Application of the Multi-Path Characteristics of Beidou GEO Satellite in SPP[J]. Geospatial Information, 2019, 17(3): 31-34 DOI:10.3969/j.issn.1672-4623.2019.03.009)
(  0) 0) |
| [2] |
刘季. 北斗GEO卫星位置计算方法探究[J]. 测绘地理信息, 2012, 37(5): 33-36 (Liu Ji. Beidou GEO Satellite Orbit Algorithm[J]. Journal of Geomatics, 2012, 37(5): 33-36)
(  0) 0) |
| [3] |
郭睿, 刘利, 李晓杰, 等. 卫星与测站钟差支持条件下的GEO卫星精密定轨[J]. 空间科学学报, 2012, 32(3): 405-411 (Guo Rui, Liu Li, Li Xiaojie, et al. Precise Orbit Determination for GEO Satellites Based on both Satellite Clock Offsets and Station Clock Offsets[J]. Chinese Journal of Space Science, 2012, 32(3): 405-411)
(  0) 0) |
| [4] |
刘俊宏. 基于双差模型的北斗GEO/IGSO/MEO混合星座精密轨道和钟差确定[D]. 长沙: 国防科学技术大学, 2016 (Liu Junhong. Precise Orbit and Clock Determination of Beidou GEO/IGSO/MEO Mixed Constellation with Double-Difference Method[D]. Changsha: National University of Defense Technology, 2016)
(  0) 0) |
| [5] |
曹芬. 基于转发测距数据的GEO导航卫星定轨方法研究[D]. 西安: 中国科学院国家授时中心, 2014 (Cao Fen. Research on Precise Orbit Determination by Transfer for GEO Navigation Satellites[D]. Xi'an: National Time Service Center, CAS, 2014)
(  0) 0) |
| [6] |
祝会忠, 郭钰铂, 张凯, 等. GEO对BDS精密单点定位的影响分析[J]. 测绘科学, 2020, 45(10): 1-9 (Zhu Huizhong, Guo Yubo, Zhang Kai, et al. Impact Analysis of GEO Satellite on BDS PPP Performance[J]. Science of Surveying and Mapping, 2020, 45(10): 1-9)
(  0) 0) |
| [7] |
张玉爽, 黄张裕, 张文祥. 北斗伪距单点定位的随机模型影响评估[J]. 测绘工程, 2017, 26(8): 24-28 (Zhang Yushuang, Huang Zhangyu, Zhang Wenxiang. The Impact Assessment of Beidou Pseudo Range Point Positioning Stochastic Model[J]. Engineering of Surveying and Mapping, 2017, 26(8): 24-28)
(  0) 0) |
| [8] |
高猛, 徐爱功, 祝会忠, 等. 非差观测模型的北斗系统实时动态定位算法[J]. 测绘科学, 2016, 41(3): 3-7 (Gao Meng, Xu Aigong, Zhu Huizhong, et al. BDS RTK Algorithm Using Undifferenced Observation Model[J]. Science of Surveying and Mapping, 2016, 41(3): 3-7)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

