2. 武汉大学卫星导航定位技术研究中心,武汉市珞喻路129号,430079
天顶对流层延迟(ZTD)是GNSS定位中的主要误差项,由于对流层不具备色散效应,因此无法像电离层那样采用双频改正的方法来消除延迟,一般采用模型或者参数估计进行改正[1]。在精密单点定位(PPP)中,对流层模型误差和气象元素误差都会对定位结果产生很大的影响,因此通常将ZTD作为待定参数进行估计。高精度的ZTD产品可以反演水汽含量,用于气象学研究[2-3],因此研究PPP反演ZTD具有重要意义。
2020-06-23北斗最后一颗全球组网卫星发射成功,至此形成了7 GEO+10 IGSO+27 MEO的星座结构。2020-07-31北斗三号全球卫星导航系统(BDS-3)正式开通,北斗进入全球服务新时代。国内外学者对BDS-2的区域服务能力和其估计ZTD的精度进行过广泛的评估分析,但缺乏对BDS全星座服务能力及ZTD估计性能的系统研究[4-6]。本文选取全球均匀分布的9个MGEX观测站的实测数据,利用自行解算的事后精密轨道和钟差产品,对BDS-3正式开通后BDS全星座的全球定位服务能力和ZTD估计性能进行评估。
1 实验方案选取全球均匀分布的9个MGEX观测站连续5 d的观测数据(2020年doy192~196)进行分析,测站分布见图 1。其中大部分测站可以观测到所有BDS-3卫星发射的信号,个别测站由于接收机硬件没有及时更新,无法跟踪2019年后发射的部分BDS-3卫星。
|
图 1 站点分布 Fig. 1 Distribution of the stations |
本文中的PPP实验基于开源的GAMP软件[7],解算策略见表 1。实验期间尚未有MGEX分析中心发布BDS全星座的精密轨道和钟差产品,因此本文采用基于武汉大学PANDA软件自行解算的GPS/BDS精密轨道和钟差产品进行PPP解算。用于GPS/BDS全星座定轨的测站分布和定轨处理策略与文献[8]一致。
|
|
表 1 PPP解算策略 Tab. 1 PPP processing strategy |
首先进行GPS静态PPP解算,评估GPS PPP收敛后的定位精度和ZTD估计精度,以验证该软件PPP算法的可靠性; 然后进行BDS静态PPP解算,将PPP定位以及ZTD估计精度与GPS进行对比,评估BDS的全球定位服务能力和ZTD估计性能。以MGEX的SNX文件中的测站坐标为坐标参考真值,以IGS提供的300 s的ZTD产品为ZTD参考真值,PPP收敛的判定采用均值变化法[9]。
2 GAMP软件PPP算法可靠性验证为了验证GAMP软件PPP算法的可靠性,对所选测站的观测数据进行GPS静态PPP解算,分析其定位精度和ZTD估计精度。
2.1 定位精度验证图 2给出了2020年doy194的PPP定位误差结果。从E、N、U误差序列可以看出,前8个测站PPP的结果都能收敛,但LMMF站高程方向和KRGG、RGDG站的E方向收敛后存在一定的系统性偏差,WUH2站高程方向在15 h后有一定程度的发散。

|
图 2 GPS PPP定位误差 Fig. 2 Positioning errors of GPS PPP |
表 2(单位mm)给出了各站PPP收敛后E、N、U方向定位误差RMS 5 d的平均值。可以看出,E方向大部分测站的RMS均值小于1 cm,KRGG站略大于1.5 cm,RGDG和WUH2站略大于1 cm,与图 2给出的单天结果一致; N方向RMS均值均小于7 mm; FFMJ、LMMF、RGDG以及WUH2站高程方向RMS均值为1~2 cm,其余测站均在1 cm以内。
|
|
表 2 GPS PPP定位误差RMS平均值 Tab. 2 Average RMS of positioning errors of GPS PPP |
图 3给出了2020年doy194的ZTD估计结果。可以看出,基于GAMP软件估计的ZTD值和IGS的对流层产品具有很好的一致性,结果相近。表 3(单位mm)给出了ZTD误差RMS 5 d的均值。可以看出,8个站的RMS均值小于1 cm,只有WUH2站的RMS均值大于1 cm,这与WUH2站的高程方向定位结果发散相关(图 2,表 2)。

|
图 3 GPS PPP估计ZTD结果 Fig. 3 ZTD values estimated by GPS PPP |
|
|
表 3 GPS PPP估计的ZTD误差RMS均值 Tab. 3 Average RMS of errors of ZTD estimated by GPS PPP |
综上分析,GAMP软件具有可靠的PPP定位结果及较优的ZTD估计精度。
3 BDS全球定位服务能力评估为评估BDS全星座的全球定位服务能力,首先对不同地区有代表性的3个测站(WUH2、KIR8以及RGDG站)2020年doy194的观测数据进行BDS-2、BDS-3和BDS-2/3的静态PPP单天解算。E、N、U方向上定位误差、可视卫星数和PDOP值见图 4,PPP收敛之后E、N、U方向的定位误差的RMS值统计见表 4(单位mm)。

|
图 4 E、N、U方向定位误差、可视卫星数和PDOP值 Fig. 4 Positioning errors in E, N, and U directions, visible satellite numbers and PDOP values |
|
|
表 4 PPP定位误差RMS Tab. 4 RMS of positioning errors of PPP |
结果显示,WUH2站BDS-2和BDS-3的可视卫星数及PDOP值相当,PPP收敛后定位精度接近,但BDS-3的收敛速度更快,这主要是因为BDS-2主要以GEO和IGSO卫星为主,卫星的几何构型变化较慢,因此PPP的收敛速度较慢。BDS-2/3组合后可视卫星数量明显增多,PDOP值也相应降低,水平方向精度与BDS-3相当,高程方向精度略优。KIR8站BDS-2可视卫星数只有5颗左右,PDOP值变化较大,收敛后N方向精度大于1 cm、高程方向精度大于2 cm,部分时间段卫星数少于4颗,进而无法单独依赖BDS-2完成连续可靠的定位解算。而BDS-3和BDS-2/3可视卫星数保持在10颗以上,其PDOP值和定位精度接近,各方向收敛后定位精度均优于1 cm。RGDG站BDS-2可视卫星数少于4颗,基本无法依赖BDS-2系统提供定位服务。而其BDS-3可视卫星数与WUH2、KIR8站基本一致,平均保持为10颗。其PPP解算收敛后水平方向上精度优于1 cm,高程方向上略大于1 cm,与BDS-2/3组合PPP定位结果相当。
表 5(单位mm)统计了各测站定位误差RMS 5 d的均值。结果显示,BDS-3和BDS-2/3 PPP收敛后定位精度接近,部分测站BDS-2/3比BDS-3 PPP收敛后的定位误差RMS值略大。已有研究证明,BDS-2与BDS-3之间存在与接收机有关的系统性偏差[14-15],由于本文没有考虑此偏差,可能会使得BDS-2/3组合结果比BDS-3单系统结果略差。除CEDU站以外,BDS-2/3水平精度整体小于1 cm,其中N方向小于8 mm; U方向精度在1 cm左右,但WIND站U方向存在明显的系统性偏差,应是接收机端的北斗天线相位中心改正不精确导致的。整体来看,BDS的定位精度已与GPS相当。
|
|
表 5 BDS-3和BDS-2/3 PPP定位误差RMS值的平均值 Tab. 5 Average RMS of positioning errors of BDS-3 and BDS-2/3 PPP |
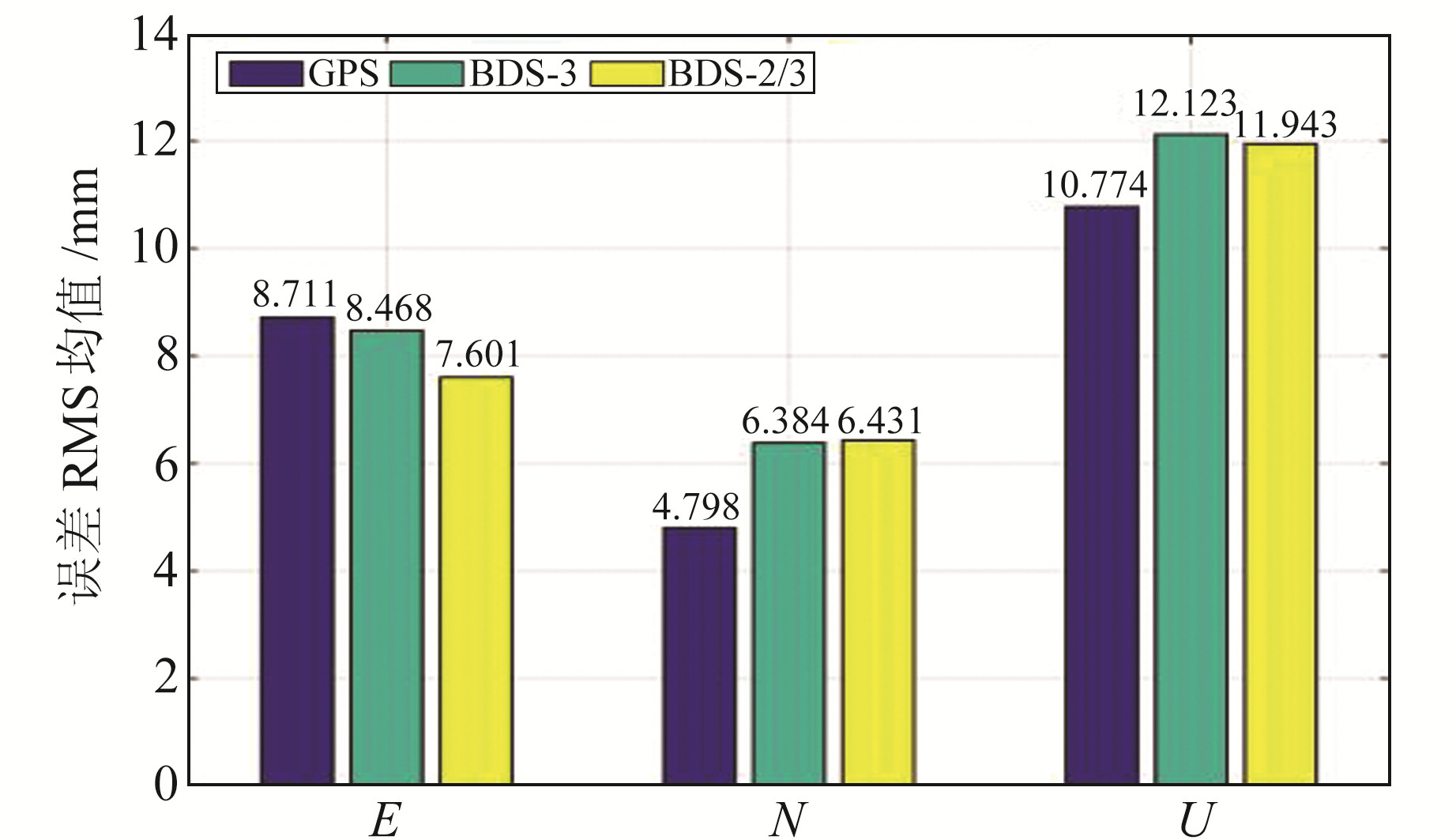
图 5给出了GPS和BDS所有测站PPP定位误差RMS 5 d的均值。整体来看,BDS的定位精度已与GPS相当,其中水平精度优于1 cm,高程精度在1 cm左右,与GPS的差值在1 mm左右。
|
图 5 PPP定位误差RMS均值 Fig. 5 Average RMS of positioning errors of PPP |
综上可知,BDS全星座已经具备了比较可靠的全球定位服务能力。
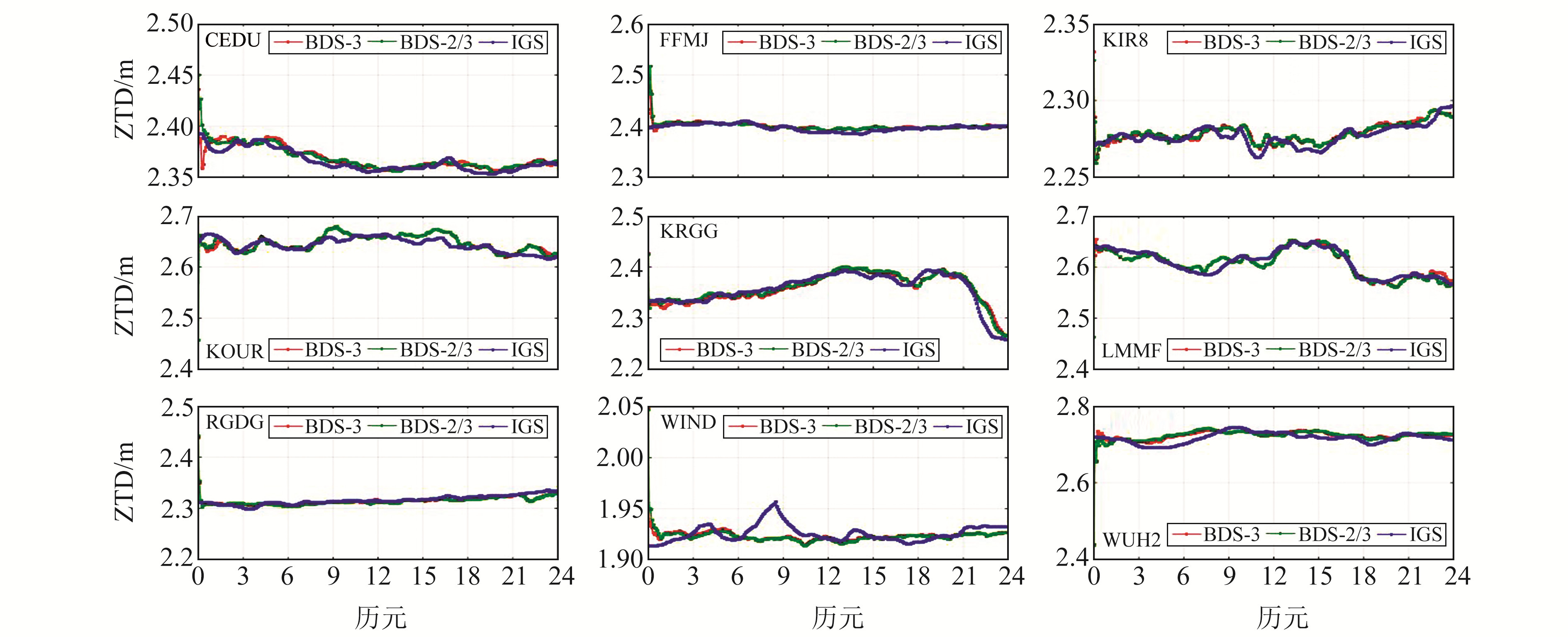
4 BDS估计ZTD性能评估图 6给出了9个MGEX观测站BDS-3、BDS-2/3在2020年doy194的ZTD估计结果。可以看出,基于BDS-3和BDS-2/3的PPP解算的ZTD值与IGS提供的对流层产品具有一致的变化趋势,且结果相近。
|
图 6 BDS PPP估计ZTD结果 Fig. 6 ZTD values estimated by BDS PPP |
表 6(单位mm)统计了BDS-3和BDS-2/3的PPP收敛后ZTD误差RMS 5 d的平均值。结果显示,基于BDS-3和BDS-2/3的ZTD估计误差接近,这与图 5的结果一致。除了LMMF和WUH2站外,其他站平均RMS值均小于1 cm。
|
|
表 6 BDS-3和BDS-2/3 PPP估计的ZTD误差RMS Tab. 6 RMS of errors of ZTD estimated by BDS-3 and BDS-2/3 PPP |
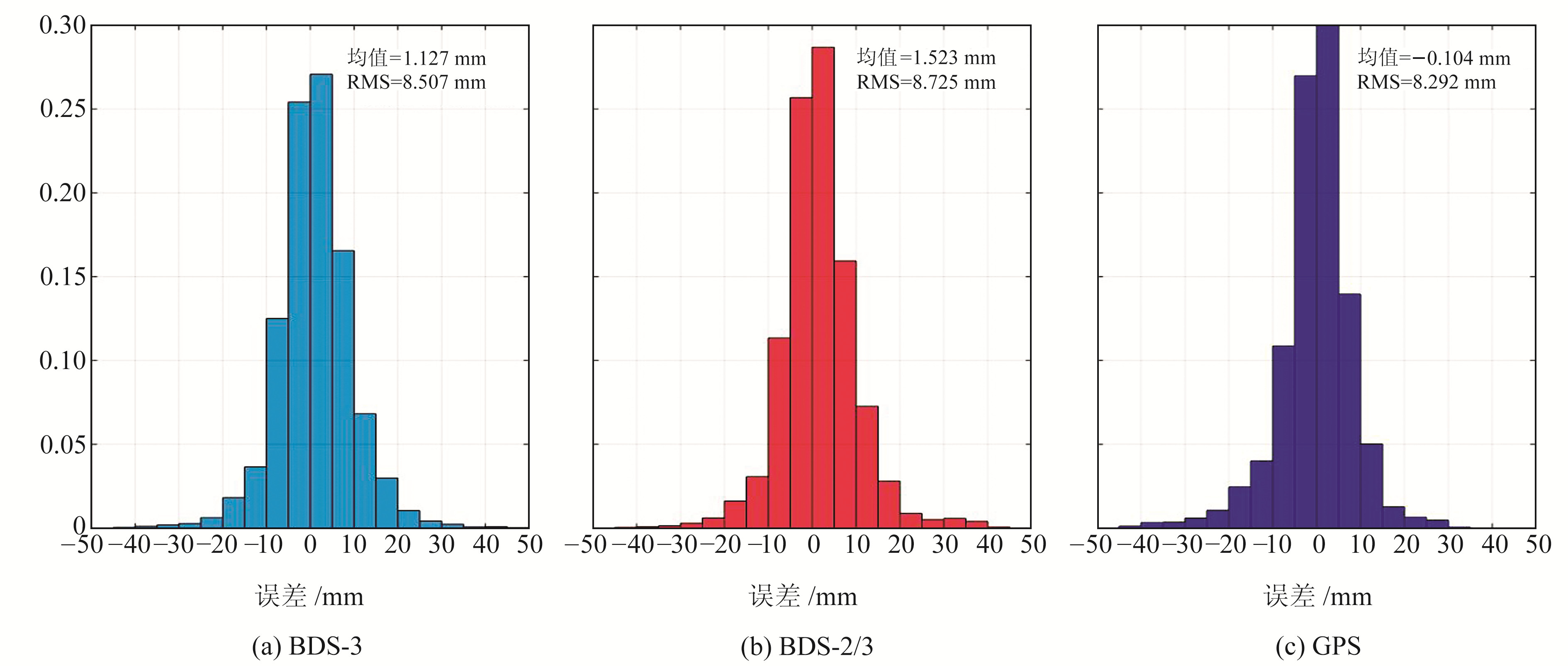
为了整体对比BDS和GPS在全球范围内的ZTD估计性能,统计9个测站PPP收敛后的ZTD估计误差,得到图 7。可以看到,BDS-3、BDS-2/3和GPS的ZTD估计误差分布基本一致,RMS值均小于1 cm。BDS-3和BDS-2/3估计的ZTD精度相当,且与GPS估计的ZTD的误差RMS差值在1 mm以内; BDS-3和BDS-2/3估计的ZTD误差均值均为1~2 mm,而GPS估计的ZTD误差均值为-0.1 mm左右,更接近0,这主要是因为当前缺乏接收机端的北斗天线相位中心改正,且IGS的对流层产品估计策略主要依赖于GPS[16]。
|
图 7 ZTD误差分布 Fig. 7 Distribution of errors of ZTD |
本文评估了BDS-3正式开通后BDS全星座的全球定位服务能力及其ZTD反演性能。首先对使用的PPP数据处理软件平台GAMP进行可靠性测试。基于GAMP软件的GPS静态PPP水平方向定位精度可以达到mm级,高程方向精度在1 cm左右,ZTD的估计精度为mm级,验证了GAMP软件PPP算法的高可靠性。然后基于GAMP软件对所选测站数据进行BDS-2、BDS-3和BDS-2/3的静态PPP解算。结果表明,BDS-2的服务范围和精度有限,BDS-3和BDS-2/3的定位精度接近,部分测站BDS-2/3比BDS-3 PPP收敛后的定位误差RMS值略大。BDS-3和BDS-2/3静态PPP水平方向精度整体优于1 cm,大部分测站高程方向精度在1 cm左右,其ZTD反演精度与GPS相当,整体可以达到mm级。总体来说,BDS系统已具备与GPS相媲美的全球定位服务能力和ZTD反演性能。
| [1] |
李征航. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2013 (Li Zhenghang. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2013)
(  0) 0) |
| [2] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15787-15801 DOI:10.1029/92JD01517
(  0) 0) |
| [3] |
Rocken C, Hove T V, Johnson J, et al. GPS/STORM—GPS Sensing of Atmospheric Water Vapor for Meteorology[J]. Journal of Atmospheric and Oceanic Technology, 1995, 12(3): 468-478 DOI:10.1175/1520-0426(1995)012<0468:GSOAWV>2.0.CO;2
(  0) 0) |
| [4] |
Xu A G, Xu Z Q, Ge M R, et al. Estimating Zenith Tropospheric Delays from Beidou Navigation Satellite System Observations[J]. Sensors, 2013, 13(4): 4514-4526 DOI:10.3390/s130404514
(  0) 0) |
| [5] |
Jiao G Q, Song S L, Ge Y L, et al. Assessment of Beidou-3 and Multi-GNSS Precise Point Positioning Performance[J]. Sensors, 2019, 19(11): 2496 DOI:10.3390/s19112496
(  0) 0) |
| [6] |
Feng P, Li F, Yan J G, et al. Evaluation of the Zenithal Total Delay Estimates from Beidou/GPS Combined Signals in the Frame of the IGS MGEX Project[J]. Acta Geodaetica et Geophysica, 2019, 54(1): 71-87 DOI:10.1007/s40328-018-0240-1
(  0) 0) |
| [7] |
Zhou F, Dong D N, Li W W, et al. GAMP: An Open-Source Software of Multi-GNSS Precise Point Positioning Using Undifferenced and Uncombined Observations[J]. GPS Solutions, 2018, 22(2): 1-10
(  0) 0) |
| [8] |
Xia F Y, Ye S R, Chen D Z, et al. Estimation of Antenna Phase Center Offsets for Beidou IGSO and MEO Satellites[J]. GPS Solutions, 2020, 24(4): 1-15 DOI:10.1007/s10291-020-01002-0
(  0) 0) |
| [9] |
周承松, 彭月, 张小红, 等. 精密单点定位收敛时间的确定方法研究[J]. 导航定位学报, 2016, 4(1): 80-87 (Zhou Chengsong, Peng Yue, Zhang Xiaohong, et al. A Study of Methods in Determining the Precise Point Positioning Convergence Time[J]. Journal of Navigation and Positioning, 2016, 4(1): 80-87)
(  0) 0) |
| [10] |
Niell A E. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B2): 3227-3246 DOI:10.1029/95JB03048
(  0) 0) |
| [11] |
Li Z S, Yuan Y B, Li H, et al. Two-Step Method for the Determination of the Differential Code Biases of COMPASS Satellites[J]. Journal of Geodesy, 2012, 86(11): 1059-1076 DOI:10.1007/s00190-012-0565-4
(  0) 0) |
| [12] |
Wang N B, Yuan Y B, Li Z S, et al. Determination of Differential Code Biases with Multi-GNSS Observations[J]. Journal of Geodesy, 2016, 90(3): 209-228 DOI:10.1007/s00190-015-0867-4
(  0) 0) |
| [13] |
Petit G, Luzum B. The IERS Conventions(2010)[R]. Bureau International des Poids et Mesures Sevres, 2010
(  0) 0) |
| [14] |
Jiao G Q, Song S L, Jiao W H. Improving BDS-2 and BDS-3 Joint Precise Point Positioning with Time Delay Bias Estimation[J]. Measurement Science and Technology, 2019, 31(2)
(  0) 0) |
| [15] |
Song Z Y, Chen J P, Wang B, et al. Analysis and Modeling of the Inter-System Bias between BDS-2 and BDS-3[C]. China Satellite Navigation Conference, Chengdu, 2020
(  0) 0) |
| [16] |
Byun S H, Bar-Sever Y E. A New Type of Troposphere Zenith Path Delay Product of the International GNSS Service[J]. Journal of Geodesy, 2009, 83(3-4): 1-7 DOI:10.1007/s00190-008-0288-8
(  0) 0) |
2. GNSS Research Center, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2021, Vol. 41
2021, Vol. 41

