2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
大气加权平均温度(Tm)是GNSS对流层水汽反演过程中计算水汽转化系数的关键参数[1],高精度的Tm可以提高可降水量(precipitation water vapor, PWV)的计算精度[2-3]。高精度的Tm可通过实测气象数据和气象数值预报资料计算获取,前者难以满足实时水汽监测的需求,而后者已被诸多学者广泛使用。
ERA5和MERRA-2再分析资料分别是ECMWF和NASA提供的最新大气再分析产品。目前对二者在中国区域内计算的Tm的精度的研究较少。因此,本文利用中国区域89个探空站2017年资料,对ERA5和MERRA-2再分析资料积分计算的Tm的精度进行评估,并分析2种资料计算的Tm的bias和RMSE的时空变化特性,为后续利用2种资料开展中国区域Tm模型构建以及水汽反演等研究提供参考。
1 数据来源 1.1 ERA5和MERRA-2再分析资料ERA5大气再分析资料(https://apps.ecmwf.int/datasets/data/interim-full-daily)可提供分层资料和地表资料,其中分层资料的水平分辨率为0.25°×0.25°(纬度×经度),时间分辨率为1 h(UTC 00:00, 01:00, …, 23:00),垂直分辨率为37层(顶层高度约为47 km); 地表资料的水平分辨率和时间分辨率与分层资料相同。选用70°~135°E、15°~50°N区域内2017年ERA5分层资料以及相应的地表资料。
MERRA-2大气再分析资料(https://goldsmr4.gesdisc.eosdis.nasa.gov/data/MERRA2) 同样提供分层资料和地表资料,其中分层资料的水平分辨率为0.5°×0.625°(纬度×经度),时间分辨率为6 h(UTC 00:00, 06:00, 12:00和18:00),垂直分辨率为42层(顶层高度约为50 km); 地表资料的水平分辨率与分层资料相同,时间分辨率为1 h(UTC 00:00, 01:00, …, 23:00)。选用70°~135°E、15°~50°N区域内2017年MERRA-2分层资料以及相应的地表资料。
1.2 无线电探空资料无线电探空资料(http://weather.uwyo.edu/upperair/sounding.html) 可提供从地面到约30 km高度范围内相应的实测分层气象数据,时间分辨率为12 h,其常作为独立观测值用来评价其他大气再分析产品和模型的精度。本文选用中国区域89个探空站2017年无线电探空资料实测数据,将利用积分法计算获得的Tm作为参考值。
2 计算原理采用积分法计算2种再分析资料中分层资料高度范围内的Tm值:
| $ {T_m} = \frac{{\int_{{h_L}}^{{h_{{\rm{top}}}}} {\left( {e/T} \right){\rm{d}}H} }}{{\int_{{h_L}}^{{h_{{\rm{top}}}}} {\left( {e/{T^2}} \right){\rm{d}}H} }} = \frac{{\sum {\left( {{e_i}/{T_i}} \right)\Delta {H_i}} }}{{\sum {\left( {{e_i}/T_i^2} \right)\Delta {H_i}} }} $ | (1) |
式中,e为水汽压,T为温度,ei为第i层大气的平均水汽压,Ti为第i层大气的平均温度,ΔHi为第i层大气的厚度,htop、hL分别为分层资料积分计算的最顶层高度和最底层高度。
| $ e = hp/0.622 $ | (2) |
式中,h为比湿,P为气压。
| $ H_p^i = \frac{{{h_{{\rm{upper}}}} - {h_{{\rm{lower}}}}}}{{\ln \left( {{P_{{\rm{lower}}}}/{P_{{\rm{upper}}}}} \right)}} $ | (3) |
式中,hupper和hlower分别为上、下层的位势高,Pupper和Plower分别为上、下层的气压。
| $ P_z^i = {P^i}\exp \left( { - \frac{{z - {h^i}}}{{{H_P}}}} \right) $ | (4) |
式中,Pz为高度z处的气压,Pi为高度h处的气压。
| $ Z = \frac{{g\left( {0, \varphi } \right)}}{{{g_0}}}\frac{{z{R_E}}}{{{R_E} + z}} $ | (5) |
式中,g0为9.806 65 J/(kg ·gpm),g(0, φ)为纬度φ处海平面g值,RE为地球半径,Z为海拔高。
利用探空站数据检验积分法计算的Tm的精度,通常先计算出探空站位置处最近4个格网点的Tm值,然后进行插值得到探空站位置处Tm,由于探空站点与再分析资料的格网点所处高度不同,水平位置也不同,若直接采用反距离加权法或双线性插值法等进行插值,会引入较大的插值误差,进而影响再分析资料的精度评估结果。因此,针对再分析资料的特性,本文提出以探空站高度为积分起算高度的方法进行积分计算,从而消除或削弱高程不同对插值的影响。但该方法需要解决2个问题:一是ERA5和MERRA-2再分析资料与探空站资料高程基准的统一; 二是再分析资料在探空站高度处的气象参数的获取。对于前者,再分析资料的高程系统为位势高,探空站的高程系统为海拔高,位势高与海拔高之间可采用式(5)进行换算,根据标准大气特性值可知,即使在50 km高度处,两者之间的偏差也小于0.8%,由此引起的大气差异可以忽略不计[4-5]; 而后者可利用再分析资料中分层资料的气象参数进行垂直插值获取,当探空站高度高于格网点高度时,气压可采用式(3)、(4)计算获得,比湿和温度等参数可采用线性内插计算获得,反之则外推,气压和比湿等参数可利用分层资料最底部3层参数外推至相应高度,温度可取平均递减率常数-6.5 K/km进行外推获得[6]。反距离加权法在Tm水平方向的插值具有较高精度[7],因此通过上述方法积分计算出探空站高度处最近4个格网点的Tm值后,采用反距离加权法对Tm水平方向进行插值可获取探空站位置处Tm值。
3 Tm精度检验 3.1 总体年均精度利用2017年中国区域89个探空站时间分辨率为12 h的数据检验2种再分析资料积分计算的Tm的精度。首先计算每个探空站在UTC 00:00和12:00时刻的Tm数据,进而得到2种再分析资料积分计算的Tm在每个探空站点处的日均bias和RMSE,最终统计得到每个探空站点处2种再分析资料积分计算的Tm的年均bias和RMSE,结果如表 1和图 1所示。bias和RMSE计算公式为:
| $ {\rm{bias = }}\frac{1}{N}\sum\limits_i^N {\left( {X_m^{{M_i}} - X_m^{{R_i}}} \right)} $ | (6) |
| $ {\rm{RMSE = }}\sqrt {\frac{1}{N}\sum\limits_i^N {{{\left( {X_m^{{M_i}} - X_m^{{R_i}}} \right)}^2}} } $ | (7) |
|
|
表 1 探空站资料检验2种再分析资料计算的Tm的精度 Tab. 1 Accuracy of Tm calculated by ERA5 and MERRA-2 reanalysis data tested by radiosonde data |
|
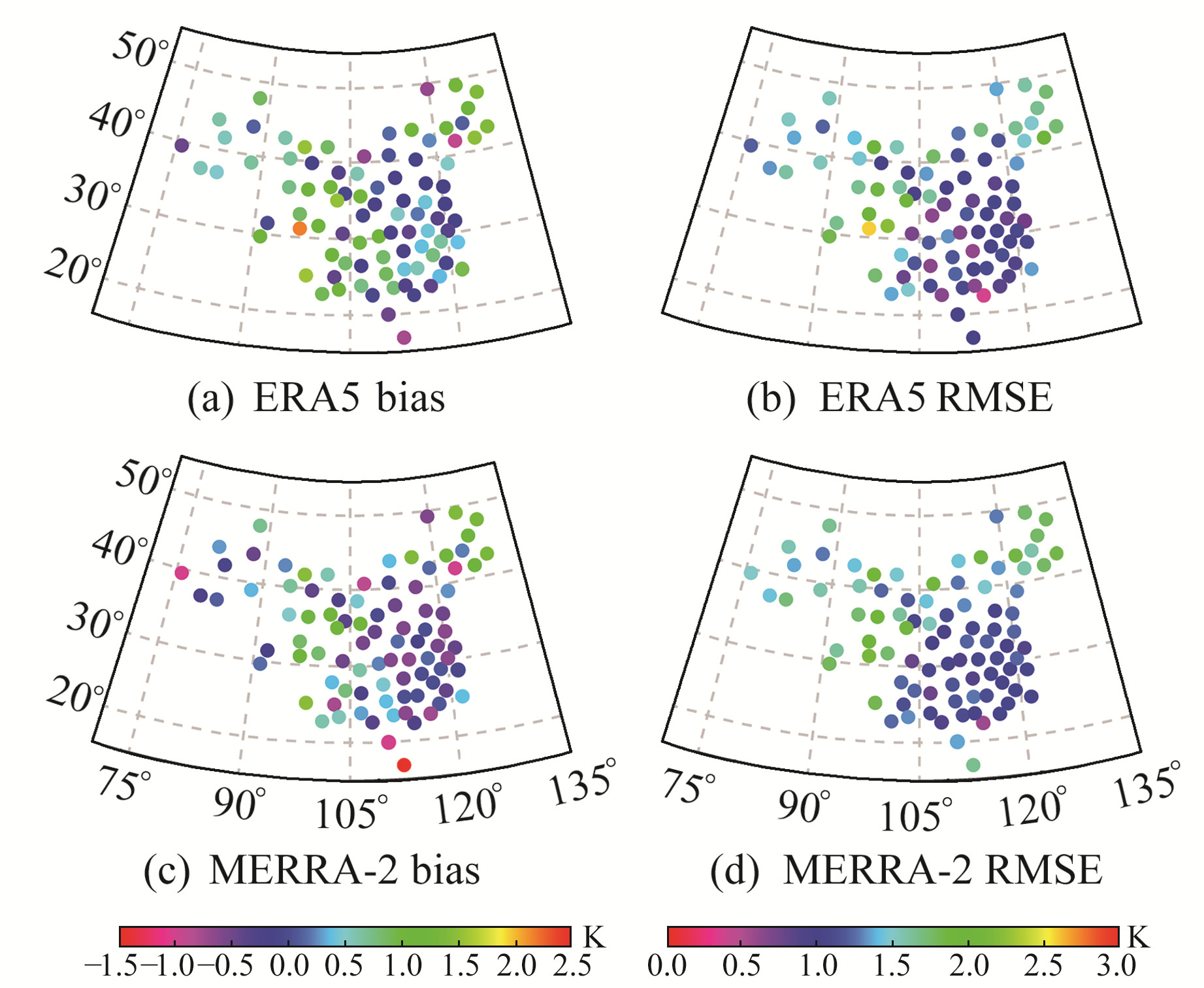
图 1 探空站数据检验2种再分析资料计算的Tm的bias和RMSE分布 Fig. 1 Distribution of bias and RMSE of Tm calculated by ERA5 and MERRA-2 reanalysis data tested by radiosonde station data |
式中,N为样本数,XmMi为再分析资料计算值,XmRi为参考值。
由表 1可知,ERA5和MERRA-2再分析资料在中国区域计算的Tm的bias变化范围分别为-0.91~2.16 K和-1.48~1.46 K,平均bias分别为0.41 K和0.10 K。由此可以看出,ERA5和MERRA-2再分析资料计算的Tm的bias均较小,其中后者的bias更小。在RMSE方面,2种再分析资料变化范围分别为0.38~2.57 K和0.58~2.12 K,平均值分别为1.26 K和1.34 K。由此表明,ERA5和MERRA-2再分析资料在中国区域计算的Tm均具有较高的精度,而前者计算的Tm的精度略高于后者,其原因可能为ERA5再分析资料的水平分辨率更高。
由图 1可以看出,ERA5再分析资料计算的Tm的bias在中国西部和北部地区主要表现为正值,表明计算的Tm值偏大,而在低纬度地区主要表现为相对较小的正值和少数较小的负值; MERRA-2再分析资料计算的Tm的bias在中国西部和北部地区主要表现为正值,表明计算的Tm值偏大,而在低纬度地区主要表现为相对较小的负值和少数较小的正值。总体上看,MERRA-2再分析资料在中国区域计算的Tm的bias更小。在RMSE方面,2种再分析资料表现相似,在低纬度地区均较小,而在中国西部和北部地区相对较大,其原因可能为中国西部和北部地区探空站稀少且分布不均,以及受到高原山地和温带季风等复杂气候的影响[8],但RMSE均在2.5 K以内。由此进一步表明,2种再分析资料在中国区域计算的Tm具有较高的精度和稳定性。
3.2 精度的时间变化特性分别在中国北部、西部和低纬度地区选取4个具有代表性的探空站,站号分别为50774(128.9°E, 47.7°N, 232 m)、51839(82.7°E, 37.1°N, 1 409 m)、58606(115.9°E, 28.6°N, 50 m)和59431(108.2°E, 22.6°N, 126 m),对2种再分析资料计算的Tm的日均bias和RMSE进行统计,结果如图 2、3所示。
|
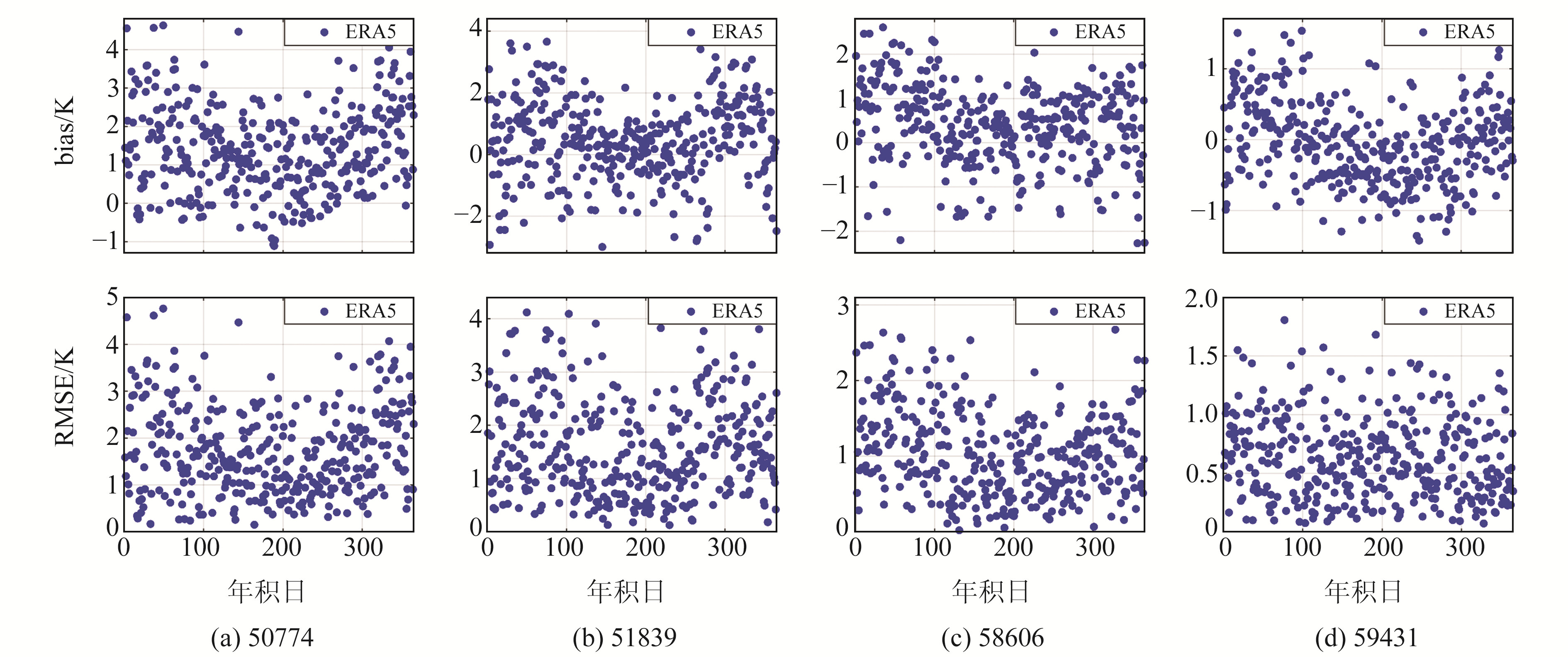
图 2 4个探空站ERA5再分析资料计算的Tm的日均bias和RMSE变化 Fig. 2 Daily bias and RMSE of Tm calculated by ERA5 reanalysis data at four radiosonde stations |

|
图 3 4个探空站MERRA-2再分析资料计算Tm的日均bias和RMSE变化 Fig. 3 Daily bias and RMSE of Tm calculated by MERRA-2 reanalysis data at four radiosonde stations |
由图 2、3可知,在中国北部和西部地区的50774站和51839站,2种再分析资料计算的Tm的日均bias表现相似,夏季bias较小,冬季bias相对较大,且主要表现为正bias,RMSE无明显变化,bias和RMSE在全年主要表现为相对较大的数值,其原因可能与前述相似; 在低纬度地区的58606站和59431站,其日均bias变化与北部和西部地区站点表现相似,但日均bias相对较小,在RMSE方面无明显变化,基本保持在2 K以内。
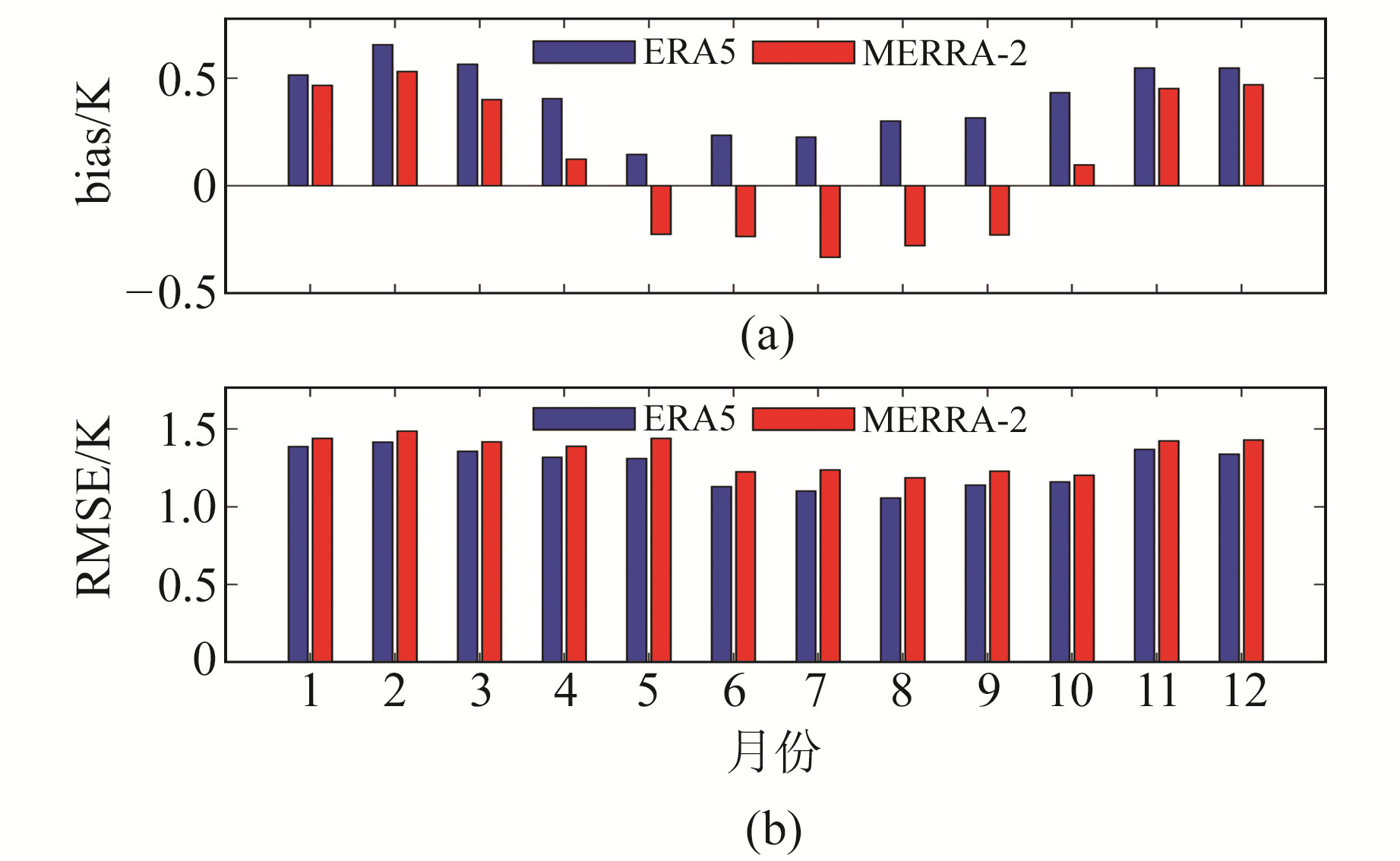
利用89个探空站数据,得到2种再分析资料计算的Tm的bias和RMSE月均值,结果如图 4所示。由图 4可知,2种再分析资料在中国区域计算的Tm的月均bias均表现出明显的季节性变化,其中ERA5再分析资料计算的Tm的月均bias在全年所有月份中均表现为正值,在夏季月份中最小,而在冬季月份中相对较大; MERRA-2再分析资料计算的Tm的月均bias在5~9月表现为负值,其余月份表现为正值,其季节性变化与ERA5再分析资料相似。总体上看,MERRA-2再分析资料计算的Tm的bias在全年大部分时间小于ERA5再分析资料。在RMSE方面,2种再分析资料计算的Tm的月均RMSE的季节性变化特征相似,即在6~10月数值较小,最小值在8月,其余月份数值相对较大。ERA5再分析资料计算的Tm的RMSE在全年均略小于MERRA-2再分析资料。综上,2种再分析资料在中国区域计算的Tm具有较高的精度。
|
图 4 中国区域探空站数据检验2种再分析资料计算的Tm的月均bias和RMSE Fig. 4 Monthly bias and RMSE of Tm calculated by ERA5 and MERRA-2 reanalysis data tested by radiosonde station data over China |
为了分析2种再分析资料计算的Tm的bias和RMSE在高程上的变化特征,根据高程对89个探空站计算的Tm的bias和RMSE进行统计,结果如图 5和表 2所示。
|
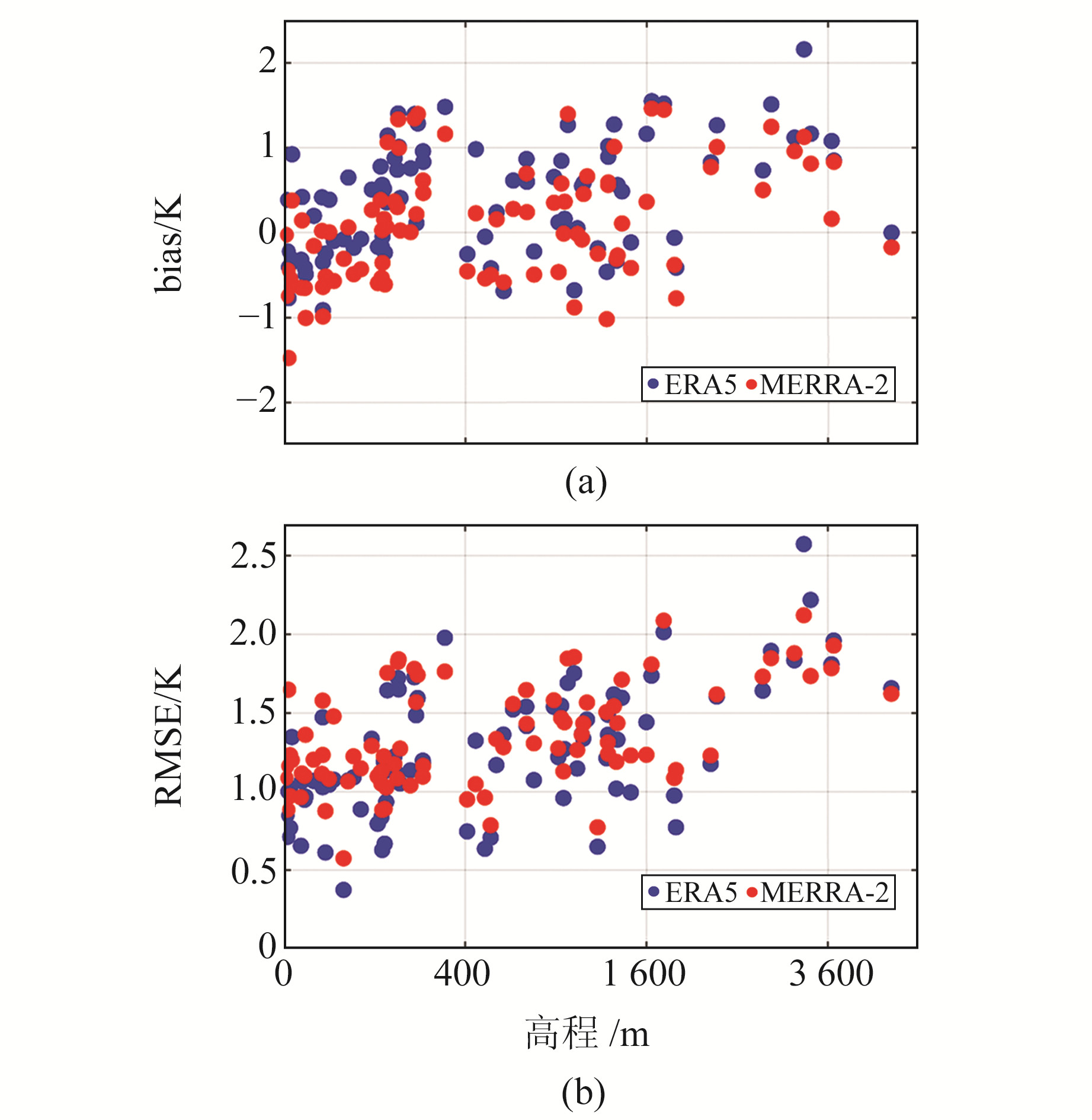
图 5 中国区域2种再分析资料计算的Tm的bias和RMSE在高程上的分布 Fig. 5 Distribution of bias and RMSE of Tm calculated by ERA5 and MERRA-2 reanalysis data at different altitudes over China |
|
|
表 2 中国区域2种再分析资料计算的Tm的bias和RMSE在不同高度区间内的统计 Tab. 2 Statistics of bias and RMSE of Tm calculated by ERA5 and MERRA-2 reanalysis data at different altitudes range over China |
由图 5和表 2可知,2种再分析资料计算的Tm的bias和RMSE在高程上均无特别明显的变化,其中位于中国西部青藏高原地区高程在3 600 m左右的极少数探空站具有相对较大的RMSE,其原因可能与前述相似。由此表明,本文提出以探空站高度为积分起算高度计算其最近4个ERA5和MERRA-2再分析资料格网点的Tm值可取得较好的效果,能极大削弱Tm在高程上插值引起的误差。在高程范围内2种再分析资料的绝对bias值基本保持在1.5 K以内,RMSE保持在2.5 K以内。尽管ERA5再分析资料的水平分辨率和时间分辨率优于MERRA-2再分析资料,但MERRA-2再分析资料计算的Tm的精度仍与ERA5再分析资料计算的Tm的精度相当,稳定性较为相似。
为了分析2种再分析资料计算的Tm的bias和RMSE在纬度上的变化,根据纬度对89个探空站计算的Tm的bias和RMSE进行统计,结果如图 6和表 3所示。

|
图 6 中国区域2种再分析资料计算的Tm的bias和RMSE在纬度上的分布 Fig. 6 Distribution of bias and RMSE of Tm calculated by ERA5 and MERRA-2 reanalysis data at different latitudes over China |
|
|
表 3 中国区域2种再分析资料计算的Tm的bias和RMSE在不同纬度区间内的统计 Tab. 3 Statistics of bias and RMSE of Tm calculated by ERA5 and MERRA-2 reanalysis data at different latitudes range over China |
由图 6和表 3可知,2种再分析资料计算的Tm的bias在纬度上分布均相对稳定,无明显变化趋势,其绝对bias值基本保持在1.5 K以内; RMSE在纬度上均表现出随纬度增加而逐渐变大的趋势,总体上仍保持在2.5 K以内。纬度上的分布特征进一步表明,MERRA-2再分析资料计算的Tm的精度和稳定性与ERA5再分析资料相似。
4 结语以中国区域89个探空站资料为参考值,ERA5和MERRA-2再分析资料计算的Tm的年均bias分别为0.41 K和0.10 K,年均RMSE分别为1.26 K和1.34 K,计算结果的精度均较高,其中ERA5再分析资料计算的Tm的精度略高于MERRA-2。
总体上看,2种再分析资料在低纬度地区精度高,在西部和北部地区精度稍低。在时间上,2种再分析资料计算的Tm的bias和RMSE均具有季节性变化,总体为夏季精度高,冬季精度稍低,其最高精度均出现在8月份,其中ERA5再分析资料计算的Tm的bias在全年均为正值,而MERRA-2再分析资料计算的Tm的bias在夏季为负值,其余时间为正值。在空间上,2种再分析资料计算的Tm的RMSE均表现出随纬度增加而逐渐变大的趋势,其中ERA5再分析资料的水平分辨率和时间分辨率均略优于MERRA-2。
利用本文提出的以探空站高度为积分起算高度的方法对再分析资料进行积分计算,可极大削弱Tm在高程上插值引起的误差。2种再分析资料计算的Tm均具有较高的精度和良好的稳定性,可作为构建中国区域Tm模型的数据源。
| [1] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15787-15801 DOI:10.1029/92JD01517
(  0) 0) |
| [2] |
王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报: 信息科学版, 2011, 36(4): 412-416 (Wang Xiaoying, Dai Ziqiang, Cao Yunchang, et al. Weighted Mean Temperature Tm Statistical Analysis in Ground-Based GPS in China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 412-416)
(  0) 0) |
| [3] |
姚宜斌, 孙章宇, 许超钤, 等. 顾及非线性高程归算的全球加权平均温度模型[J]. 武汉大学学报: 信息科学版, 2019, 44(1): 106-111 (Yao Yibin, Sun Zhangyu, Xu Chaoqian, et al. Global Weighted Mean Temperature Model Considering Nonlinear Vertical Reduction[J]. Geomatics and Information Science of Wuhan University, 2019, 44(1): 106-111)
(  0) 0) |
| [4] |
章传银, 郭春喜, 陈俊勇, 等. EGM 2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283-289 (Zhang Chuanyin, Guo Chunxi, Chen Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289 DOI:10.3321/j.issn:1001-1595.2009.04.001)
(  0) 0) |
| [5] |
Jiang P, Ye S R, Chen D Z, et al. Retrieving Precipitable Water Vapor Data Using GPS Zenith Delays and Global Reanalysis Data in China[J]. Remote Sensing, 2016, 8(5): 389 DOI:10.3390/rs8050389
(  0) 0) |
| [6] |
Wang X M, Zhang K F, Wu S Q, et al. Water Vapor-Weighted Mean Temperature and Its Impact on the Determination of Precipitable Water Vapor and Its Linear Trend[J]. Journal of Geophysical Research: Atmospheres, 2016, 121(2): 833-852
(  0) 0) |
| [7] |
谢劭峰, 黎峻宇, 刘立龙, 等. 新疆地区GGOS Atmosphere加权平均温度的精化[J]. 大地测量与地球动力学, 2017, 37(5): 472-477 (Xie Shaofeng, Li Junyu, Liu Lilong, et al. Refinement of GGOS Atmosphere Weighted Mean Temperature in Xinjiang[J]. Journal of Geodesy and Geodynamics, 2017, 37(5): 472-477)
(  0) 0) |
| [8] |
Huang L K, Liu L L, Chen H, et al. An Improved Atmospheric Weighted Mean Temperature Model and Its Impact on GNSS Precipitable Water Vapor Estimates for China[J]. GPS Solutions, 2019, 23(2)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2021, Vol. 41
2021, Vol. 41


