2. 上海市地震局,上海市兰溪路87号,200062;
3. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077
随着我国地震监测网络不断加密,地震观测数据成倍增长,传统地震检测方法如人工识别和基于长短时间平均(STA/LTA)[1]已无法满足大数据时代地震数据自动化和智能化处理的要求。有关学者基于波形相似性提出波形互相关[2]以及指纹和相似性阈值[3](FAST)等方法,但这些方法均具有一定的局限性,因此发展新的快速及自动化地震检测方法成为大数据时代海量地震数据处理和应用的关键之一。
随着人工智能技术的快速发展,机器学习在地震学中具有广泛的应用前景[4]。深度卷积神经网络(CNN)已被成功应用于地震拾取、震相判别等方面,如ConvNetQuake[5]、PhaseNet[6]、Unet_cea[7]等,这些模型在检测精度、计算速度、自动化程度等方面均大大超越传统算法。目前已有关于各类地震检测机器学习模型的研究,但均基于海量地震数据,只有在地震活跃、测震台站密集且连续观测时间长的地区才有可能收集到足够多的地震数据,且海量地震事件的整理、人工标注和筛选工作需要消耗大量人力和时间,成本较高。训练数据来源区较为单一也可能造成部分已有模型的泛化性能不佳。
针对上述问题,从研究适用小样本情况即采用较少地震数据进行训练的新模型出发,本文提出本地地震检测机器学习模型CCLSN(CWT-CNN local seismological network)。首先阐述联合应用连续小波变换和轻量化卷积神经网络的设计思路,然后在开源机器学习框架下实现模型,最后采用浙江文成珊溪水库监测台网中3个台站2014年的震群数据对模型进行测试和检验,并与深度卷积神经网络的代表模型ConvNetQuake进行对比,论证新模型的可行性和性能优势。
1 设计思路 1.1 应用连续小波变换降低检测问题的难度地震检测本质上为分类问题,对象特征信息越简明则难度越低,且所需的训练样本数量相对越少。大多数已发表的地震检测机器学习模型[5-7]将地震原始波形作为模型输入,地震原始波形为时序一维数据,其包含的地震信号和噪声信号的特征均被压缩在一维时域范围内,由于地震事件和噪声记录在本质上具有不同的频谱内容,通过学习波形数据的时频特征能降低区分地震事件和噪声信号的难度[8]。CCLSN应用连续小波变换将一维波形时序数据转化为二维时频矩阵数据,通过将输入的数据转换为对地震检测任务更为有利的状态来降低检测问题的难度,达到减少训练所需样本数量的目的。
1.2 轻量化卷积神经网络最新研究表明[9],对于卷积神经网络而言,地震特征不一定为高度抽象的对象,使用层数较少的神经网络也能获得与深度神经网络相近的性能。较少的网络层数和较简单的模型使模型参数相比于深度网络模型明显减少,从而使训练所需的样本数大幅降低。
目前已发表的各类地震检测机器学习模型层数大多为8~10层,ConvNetQuake为9层,Unet_cea为8层。CCLSN具有重新设计的轻量化卷积神经网络,该网络包含2个卷积单元层和1个全连接层以及输入端的连续小波时频转换层,层数较已有模型降低一半以上,模型的简化使参与计算的模型参数大幅减少。同时,对卷积单元进行重新设计,常见的卷积单元包含卷积层、激活函数和池化层,CCLSN在卷积层和激活函数之间增加1个批量标准化层(batch normalization, BN)。BN层可对前一层的输出项进行标准化操作,使每个卷积层的数值均能在有效范围内进行传递,增强网络的稳定性,降低对学习速率的要求,从而加快训练速度;同时也可以取消dropout(随机失活)和L2正则项参数,减少需要人为设定的超参数数量。减轻训练数据可减少过拟合现象,确保模型性能不会随着训练数据的减少而降低。
2 模型实现 2.1 概述CCLSN模型结构可分为4层,第1层为连续小波时频转换(continuous wavelet transform, CWT)层,其他3层为轻量化卷积神经网络(lightweight CNN),包括2个卷积单元层和1个全连接层,最后通过Sigmoid函数输出检测概率。
2.2 CWT层CWT层通过连续小波变换将输入的三分量一维时序数据转换为三分量二维时频矩阵数据。除必要的归一化和窗口化之外,既有模型常对输入数据进行额外预处理操作,如带通滤波等。滤波可改善信噪比,但也可能造成波形形态变化,甚至是相移[10],不利于后续的震相判断和拾取工作。为了尽可能准确地反映原始信号的时频特性,CCLSN将原始采样信号作为CWT层的输入,小波基选择Complex Morlet小波[11],该小波为单频复正弦调制高斯波,在时频两域均具有良好的分辨率,常用于地震资料分析领域。图 1为地震事件和背景噪声时序数据通过CWT变换后的对比情况。

|
(b)为该站同日记录的背景噪声; (c)~(e)为(a)中地震事件的CWT变换; (f)~(h)为(b)中背景噪声的CWT变换 图 1 2014-09-15浙江HL台记录到ML1.2地震事件 Fig. 1 ML1.2 earthquake recorded by HL station in Zhejiang province on 2014-09-15 |
考虑到测震仪器的响应特性和地震信号的频域特点,同时兼顾计算效率,计算频域取0~45 Hz。为使后续轻量化卷积神经网络的输入数组结构更加规整,输出端在时域内进行适当降采样处理。
2.3 轻量化卷积神经网络CCLSN轻量化卷积神经网络包含2个卷积单元层和1个全连接层,每个卷积单元包括卷积层、BN层、激活函数和池化层。卷积层(conv)将输入数据与卷积过滤器作卷积运算进行特征提取,本文使用尺寸为5×5×m的卷积滤波器,表达式为:
| $ \begin{array}{l} U_{f, t, c}^i = b_c^i + \sum\limits_{f' = 1}^5 {\sum\limits_{t' = 1}^5 {\sum\limits_{c' = 1}^m {Z_{f + f', t + t', c'}^{i - 1}} } } \cdot \\ W_{f', t', c', c}^i, i \in \left\{ {1, 2} \right\} \end{array} $ | (1) |
式中,上标i为卷积层数,Zi-1和Ui分别为第i层的输入和输出数据,Wi为储存该层卷积滤波器的权重,bi为储存该层的偏差,下标f、t、c分别为数组的频域轴、时域轴和通道轴索引,m为输入数据的通道数。所有卷积均使用零填充(zero padding)作为边界条件,卷积滤波器的个数取12个。
BN层可对卷积层输出数组进行标准化,即使其均值接近0、标准差接近1,可表示为:
| $ {\rm{BN}}\left( U \right) = \gamma \frac{{U - \bar U}}{{\sqrt {{\rm{var}}\left( U \right)} }} + \beta $ | (2) |
式中,
池化层(pooling)可用于压缩参数数量,CCLSN池化层采用最大池化(max pooling),表达式为:
| $ \begin{array}{l} Z_{f, t, c}^i = {\rm{max}}\{ R_{pf + f', qt + t', c}^i|f' \in \left[ {0, p - 1} \right], \\ t' \in \left[ {0, q - 1} \right]\} \end{array} $ | (3) |
式中,[p, q]为频域轴和时域轴的池化步长。
卷积神经网络通常侧重于数组特征的空间相关性而对位置不敏感[12],地震事件的信号特征在频率域上具有相似的分布,而在时间域上,训练样本的人工标注必然存在一定偏差。为了使模型对频域敏感而对时域不敏感,CCLSN在池化层中对频域和时域设置不同的下采样步幅,即式(3)中步长[p, q]设置为[1, 2],每一池化层之后数组沿时间轴维度减半而频域轴保持不变。
卷积单元的输出数组降维平整化后将传递到完全连接(fully connected, FC)层,该层具有与普通神经网络相同的形式,用于将之前2个卷积单元获得的特征表达向量映射到最终的输出函数。
2.4 输出函数FC层的输出反馈到输出函数可用于计算样本适当归一化的类别概率分布,输出函数选择Sigmoid函数,输出样本[0, 1]之间的检测概率,据此判别样本属于地震事件还是背景噪声。CCLSN模型结构如图 2所示。
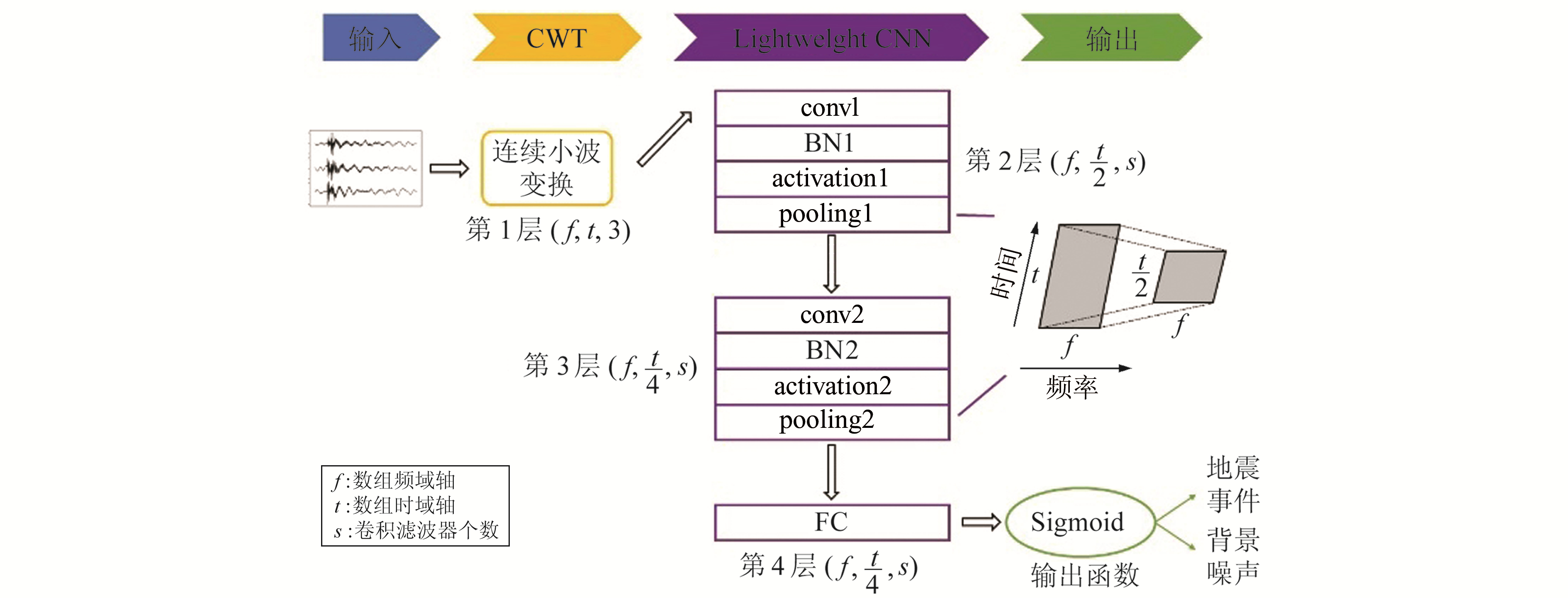
|
图 2 CCLSN模型结构 Fig. 2 Model structure of CCLSN |
CCLSN采用二元交叉熵(binary_crossentropy)损失函数,通过梯度下降法最小化代价函数来更新模型的网络参数。为了加快模型的训练速度并提高其鲁棒性,采用Adam算法优化训练过程,使用mini-batch梯度下降法将训练集分批次输入模型进行训练,每个批次的训练集样本数均设定为128,训练轮次设定为30。为了使模型能够适应不同样本数量、不同难度的训练任务,通过设置提前结束(early stopping)使其在精度不再提高时自动结束训练过程,提前结束的条件设置为连续2轮训练代价函数降低小于0.03。由于采用Adam优化算法和设置提前结束,该模型具有较大的学习速率,因此将学习速率设定为0.01。
本文使用TensorFlow及Keras框架来实现CCLSN,在NVIDIA GeForce GTX 1070Ti图形处理单元上进行训练和测试。模型源码储存在https://github.com/abcdef1991/CCLSN.git。
3 性能测试 3.1 测试数据本文使用浙江省文成县珊溪水库监测台网中YS、HL、TSH三个台站2014-09的震群记录作为测试数据。珊溪水库位于浙东南褶皱带温州-临海坳陷南部,2014-09~12震群主要呈NW向分布在双溪-焦溪垟断裂南侧[13],3个台站距震群中心约8 km、11 km和15 km(图 3)。YS台地震计型号为FSS-3B,采样率为100 Hz;HL台地震计型号为BBVS-60,采样率为50 Hz;TSH台地震计型号为BBVS-60,采样率为100 Hz。每个台站的波形记录包含3个通道,分别对应3个空间维度:HN为南北向、HE为东西向、HZ为垂直向。
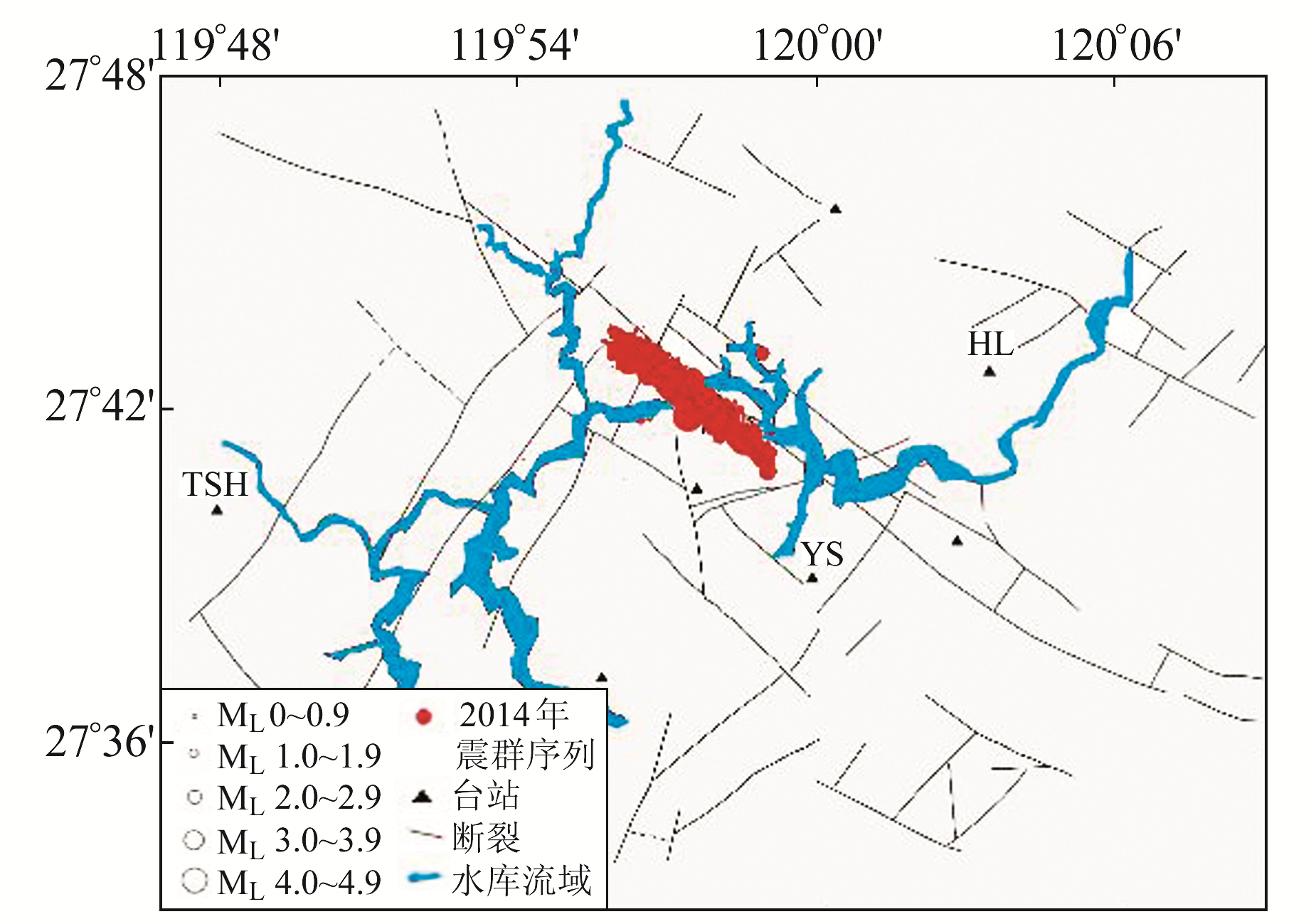
|
图 3 珊溪水库监测台网及水库2014年震群活动分布 Fig. 3 Shanxi reservoir monitoring network and earthquake swarm activity in 2014 |
通过窗口化与归一化预处理从连续波形数据中提取数据集样本,从数据流中提取2种类型的40 s时长窗口——地震事件窗口和背景噪声窗口,对每个窗口进行归一化(三通道独立)。通过地震目录选择事件窗口,在目录地震之间选择噪声窗口,每个台站在2014-09-12~2014-09-26共产生500个事件窗口和同等数量的噪声窗口,根据窗口类型对每个窗口按事件/噪声进行分类,共计1 000个带标签的窗口样本组成实验数据集,该训练集中带标签的样本数量相比于已发表模型的样本数低一个以上数量级。
将实验数据集划分为训练集和测试集2个独立的分布集,训练集包括前400个事件和同等数量的噪声窗口,测试集包括后100个事件和同等数量的噪声窗口。不同于许多已有研究中训练集和测试集来自同一分布[5-7],本文训练集和测试集按时间先后采用不同分布划分,这样可更接近实际应用中采用过去数据训练模型然后检测未来数据的模式,测试的结果更具有实际参考价值。
3.3 小型训练集下的性能检测将训练集数据作为输入进行模型训练,训练完成后在测试集上进行检测,以检测结果与测试集真实标签之间的差异程度来反映模型的检测性能。图 4为3个台站测试集的检测概率及其分布。

|
检测概率[0, 0.5)判别为噪声,[0.5, 1]判别为地震 图 4 测试集检测概率及其分布 Fig. 4 Prediction probability of test set and its distribution |
表 1为测试结果的混淆矩阵,从表中可以看出,模型对于地震事件的识别精度平均为97.69%,对背景噪声的识别精度平均为98.66%,均高于ConvNetQuake在俄克拉荷马州94.8%的检测精度;地震事件的召回率平均为98.67%,背景噪声的召回率平均为97.67%。对于单个台站,模型的识别精度分别为98.02%(HL)、97.00%(TSH)、99.51%(YS),召回率分别为98.00%(HL)、97.00%(TSH)、99.50%(YS),平均精度为98.18%,平均召回率为98.17%,超过98%的测试集窗口被正确分类,模型的检测性能在已发表的各种机器学习方法中处于领先水平。
|
|
表 1 HL、TSH、YS台测试集混淆矩阵 Tab. 1 Confusion matrix of test set for HL, TSH, YS |
3个台站测试集精度的极差为2.51%,平均差为0.887%;召回率的极差为2.50%,平均差为0.889%。虽然3个台站的位置、震中距各不相同,安装的仪器型号和采样率也存在差异,但模型在3个台站均具有高精度的检测性能,不同台站间检测性能波动较小,体现出较好的一致性和鲁棒性。图 5为模型在连续波形上检测到的地震事件。
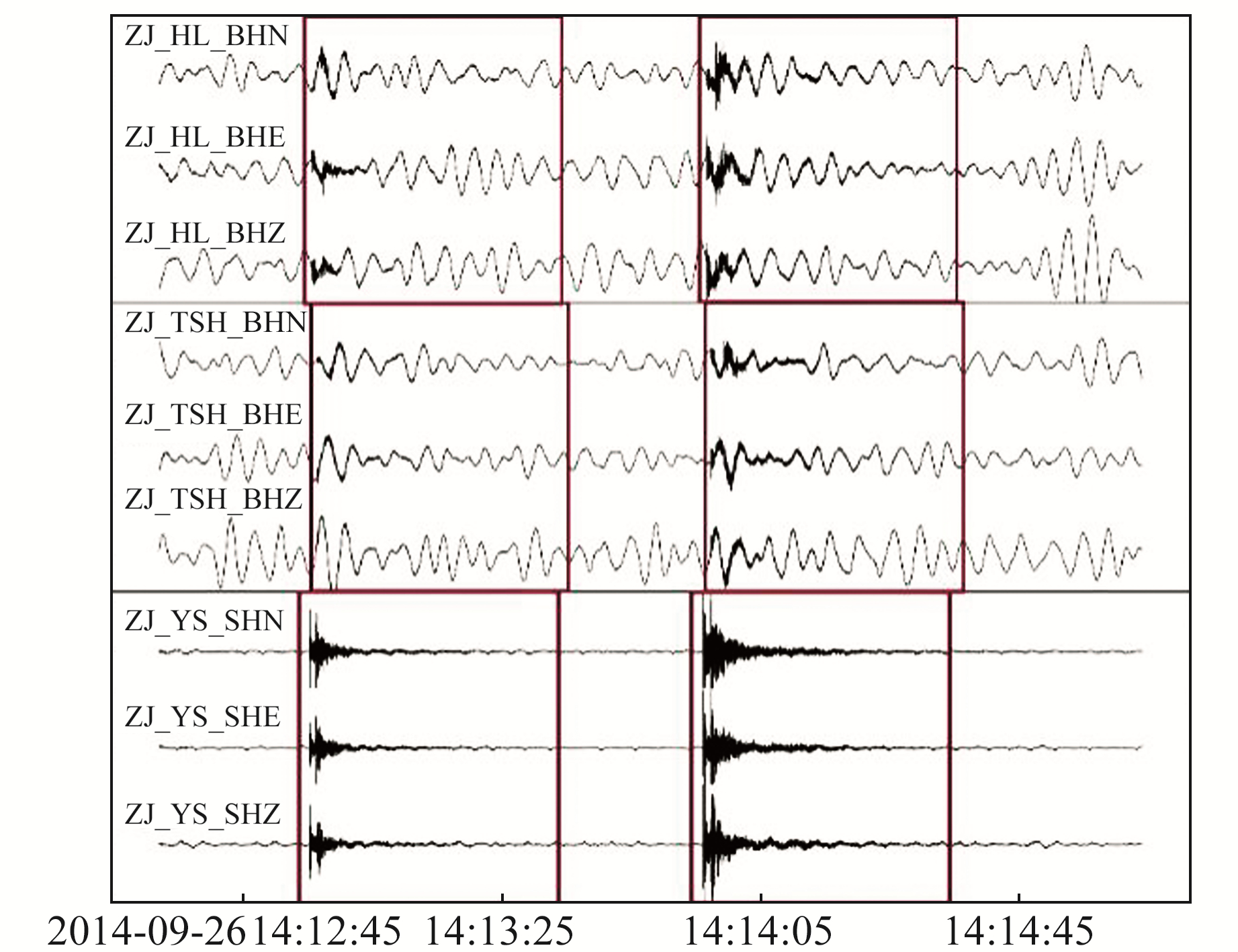
|
红框为检测到的地震事件窗 图 5 CCLSN在连续波形上检测到地震事件示例 Fig. 5 An example of seismic detection in continuous waveform using CCLSN |
在相同平台上采用同样训练集训练Perol等[5]提出的ConvNetQuake模型并进行测试,表 2为训练和测试对比情况。ConvNetQuake在3个台站的平均精度和召回率比CCLSN低16%以上,在HL、TSH台的精度和召回率小于80%,表明在数百样本量的小样本情况下,ConvNetQuake无法获得理想性能。在单台训练时间方面,ConvNetQuake为29 s,CCLSN为18 s,这与模型深度的减少和提前结束等技术的应用有关,CCLSN的训练时间成本较ConvNetQuake有进一步下降。
|
|
表 2 CCLSN与ConvNetQuake性能对比 Tab. 2 Performance comparison between CCLSN and ConvNetQuake |
本文提出一种地震检测机器学习新模型CCLSN,通过对地震原始波形进行连续小波时频变换和使用重新设计的轻量化卷积神经网络,实现适用于小样本情况和大幅度降低训练所需样本数量的目标。测试结果表明,CCLSN仅用包含数百个地震事件窗和背景噪声窗的小型数据集,可实现稳定和高精度的检测性能。在数据集样本数上,该模型比已有的各种机器学习模型降低至少一个数量级,训练的时间成本也有所降低;在检测性能上,精度和召回率均在98%以上,不同台站间波动较小,体现出良好的鲁棒性和稳定性。在使用小样本数据进行训练的情况下,CCLSN在模型性能和训练成本上具有明显优势。
对于实验区以外的地区,CCLSN可利用其适用小样本的特性,使用本地较少的有标注的地震数据训练本地地震检测模型,以获得理想的检测性能,实现本地地震数据的自动化和智能化处理。对于我国中东部等少震弱震地区,现有的有标注的地震数据往往不足以建立大型地震数据集,CCLSN可为这些地区实现自动化地震检测提供一种新的技术途径。模型的部署方式,即基于单台还是区域台网,需根据模型的迁移性能和实际需求情况决定,这有待在后续应用研究中进一步讨论。
致谢: 感谢浙江省地震局地震监测预报研究中心提供测试数据。
| [1] |
Allen R V. Automatic Earthquake Recognition and Timing from Single Traces[J]. Bulletin of the Seismological Society of America, 1978, 68(5): 1 521--1 532
(  0) 0) |
| [2] |
Schaff D P, Richards P G. Lg-Wave Cross Correlation and Double-Difference Location: Application to the 1999 Xiuyan, China, Sequence[J]. Bulletin of the Seismological Society of America, 2004, 94(3): 867-879 DOI:10.1785/0120030136
(  0) 0) |
| [3] |
Yoon C E, O'Reilly O, Bergen K J, et al. Earthquake Detection through Computationally Efficient Similarity Search[J]. Science advances, 2015, 1(11): 1 501-1 057
(  0) 0) |
| [4] |
Pezzo E, Esposito A, Giudicepietro F, et al. Discrimination of Earthquakes and Underwater Explosions Using Neural Networks[J]. Bulletin of the Seismological Society of America, 2003, 93(1): 215-223 DOI:10.1785/0120020005
(  0) 0) |
| [5] |
Perol T, Gharbi M, Denolle M. Convolutional Neural Network for Earthquake Detection and Location[J]. Science Advances, 2018, 4(2): 1 700 578 DOI:10.1126/sciadv.1700578
(  0) 0) |
| [6] |
Zhu W Q, Beroza G C. PhaseNet: A Deep-Neural-Network-Based Seismic Arrival-Time Picking Method[J]. Geophysical Journal International, 2019, 216(1): 261-273
(  0) 0) |
| [7] |
赵明, 陈石, 房立华, 等. 基于U形卷积神经网络的震相识别与到时拾取方法研究[J]. 地球物理学报, 2019, 62(8): 3 034-3 042 (Zhao Ming, Chen Shi, Fang Lihua, et al. Earthquake Phase Arrival Auto-Picking Based on U-Shaped Convolutional Neural Network[J]. Chinese Journal of Geophysics, 2019, 62(8): 3 034-3 042)
(  0) 0) |
| [8] |
Vaezi Y, van der Baan M. Comparison of the STA/LTA and Power Spectral Density Methods for Microseismic Event Detection[J]. Geophysical Journal International, 2015, 203(3): 1 896-1 908 DOI:10.1093/gji/ggv419
(  0) 0) |
| [9] |
Mignan A, Broccardo M. Neural Network Applications in Earthquake Prediction (1994-2019): Meta-Analytic and Statistical Insights on Their Limitations[J]. Seismological Research Letters, 2020, 91(4): 2 330-2 342 DOI:10.1785/0220200021
(  0) 0) |
| [10] |
Diehl T, Kissling E, Bormann P. Tutorial for Consistent Phase Picking at Local to Regional Distances[M]//Bormann P. New Manual of Seismological Observatory Practice (NMSOP-2). Potsdam: GFZ, 2012
(  0) 0) |
| [11] |
Goupillaud P, Grossmann A, Morlet J. Cycle-Octave and Related Transforms in Seismic Signal Analysis[J]. Geoexploration, 1984, 23(1): 85-102 DOI:10.1016/0016-7142(84)90025-5
(  0) 0) |
| [12] |
Nakano M, Sugiyama D, Hori T, et al. Discrimination ofSeismic Signals from Earthquakes and Tectonic Tremor by Applying a Convolutional Neural Network to Running Spectral Images[J]. Seismological Research Letters, 2019, 90(2): 530-538
(  0) 0) |
| [13] |
王鹏, 孙冬军, 任烨, 等. 浙江珊溪水库2014年震群活动发震机理研究[J]. 地震学报, 2017, 39(5): 648-658 (Wang Peng, Sun Dongjun, Ren Ye, et al. Investigation on the Seismogenic Mechanism of the 2014 Earthquake Swarm in Shanxi Reservoir, Zhejiang Province[J]. Acta Seismologica Sinica, 2017, 39(5): 648-658)
(  0) 0) |
2. Shanghai Earthquake Agency, 87 Lanxi Road, Shanghai 200062, China;
3. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China
 2021, Vol. 41
2021, Vol. 41


