地球重力场信息可反映地球表面载荷以及内部物体质量的分布变化,是大地测量学、地球物理学等学科研究的重要组成部分[1]。2002-03美国宇航局NASA以及德国航空航天中心DLR联合研制发射GRACE地球重力场观测卫星,以前所未有的精度绘制全球静态重力场[2]。由全球时变重力场模型反演得到的等效水高等数据,已在区域地下水存量、冰川融化、地表载荷变化趋势等领域取得广泛应用[3-5]。因此对等效水高以及地表形变量进行精准预测,能够极大推进地表水存储量、地表质量变化等各方面预测研究。
由于时间序列特征复杂,基于统计学的传统方法难以具备较好的预测效果。循环神经网络(recurrent neural network, RNN)可提供一种全新的预测方法, 但RNN网络在训练过程中容易出现梯度消失或梯度爆炸的现象,并且无法学习到时间序列之间长时期的依赖特征[6]。Hochreiter等[7]对RNN网络进行改进,推出LSTM长短时记忆网络,可克服相关问题, 预测效果显著提升。基于LSTM的时间序列预测在各个领域蓬勃发展, 改进的LSTM网络在地震横波速度预测方面具有较高的精度和较强的泛化能力[8], 在海洋畸形波预测方面比传统支持向量机算法更加精准[9];在自然灾害领域,LSTM可用于预测降水、干旱等气象灾害[10-13]。目前关于GRACE反演产品的研究主要集中在应用方面, 在预测方面的研究较少, 此外LSTM在地球科学方面的应用大部分采用单层LSTM结合传统方法或改进网络内部结构的方法,从而忽视了LSTM能够拓展成深层网络的特点。基于以上情况,本文利用GRACE月时变重力场信息,反演等效水高及地表位移量的月序列值;通过拼接多个LSTM网络构成深度LSTM网络,使用遗传算法预训练优化网络结构,再对等效水高等数据进行预测;并以长江、三峡和亚马逊流域作为实验区域开展实验,验证深度网络的泛化能力。
1 GRACE数据处理本文采用德克萨斯大学空间研究中心CSR推出的Level-2-Rlease-06数据集,包含2002-04~2017-06共163个月(部分月份数据缺失)最高阶为60的月球谐系数集。GRACE卫星无法确定球谐系数C20项的精确值,需用卫星激光测距SLR(satellite laser ranging)得到的解来代替[14],球谐系数一阶项需要替换为由Swenson等[15]的方法得到的计算值, 采用半径300 km的高斯滤波对高阶噪声进行去噪处理[16],同时采用P4M6去条带方法去除球谐系数的相关性[17],地表等效水高的具体计算公式可参考文献[18]。
此外, 球谐系数的频谱域截断相当于空间域的低通滤波,并且去条带和高斯滤波都可能会使目标区域的信号向外泄露或周围区域的信号泄露至目标区域,使给定区域的平均估计值出现偏差, 因此需要进行校正。本文研究的主要目标是针对给定的等效水高序列,如何更为精准地由该序列的本身规律去推知其未来趋势,因此对于获得给定序列的处理方式较为粗糙,并且未考虑气候变化、地震等因素对地表位移量的影响, 而在实际应用中需要更为精准地处理并考虑具体因素的影响。地表垂直、水平方向位移量的计算公式可参考文献[19]。
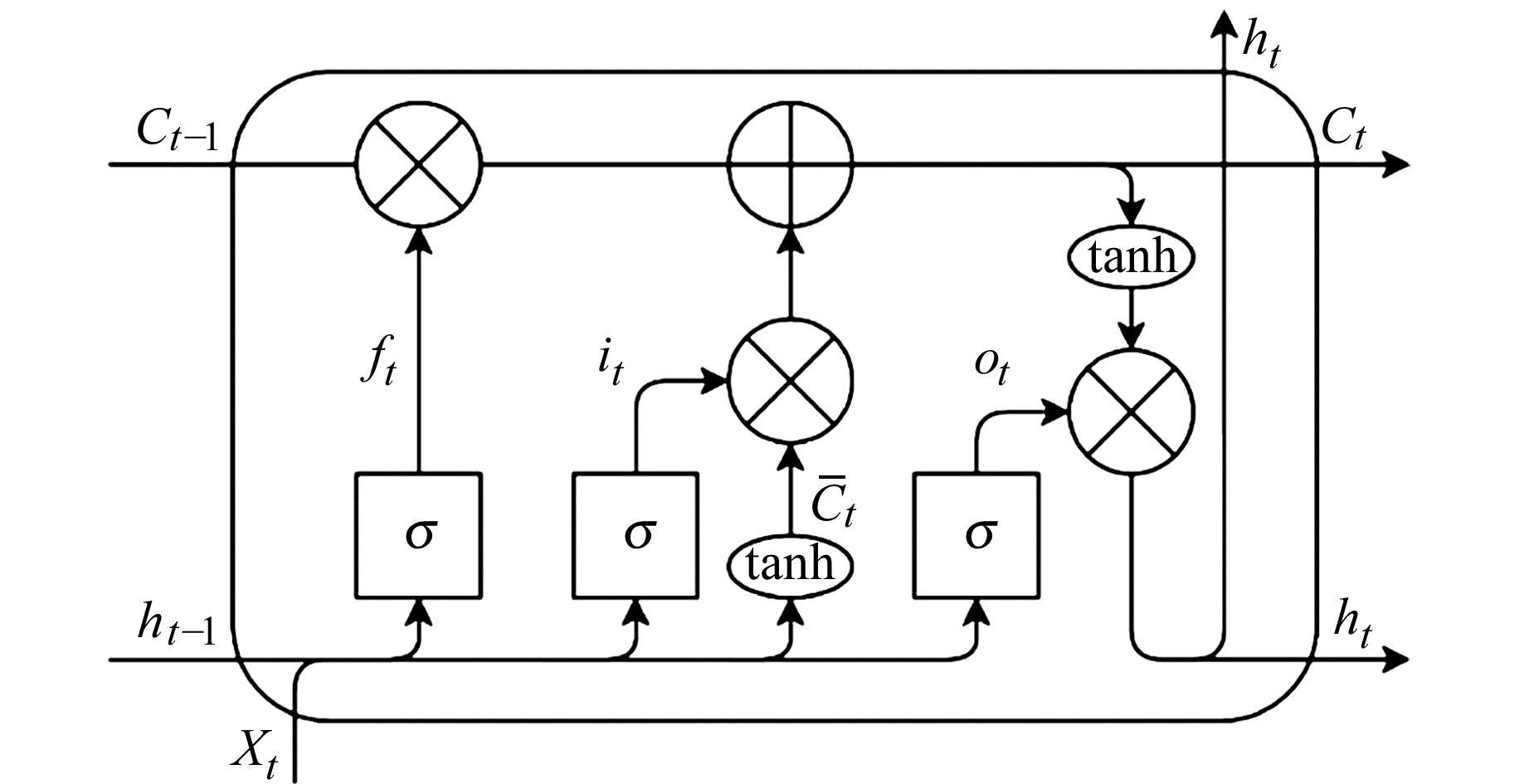
2 模型搭建 2.1 LSTM网络基本原理简单RNN结构只能记录相邻间隔的时间信息,LSTM在RNN基础结构上具有较大革新,可克服长期依赖问题, 具有长期记忆力。LSTM的核心是记忆细胞状态以及决定记忆细胞记住或忘记哪些信息的门结构,决定记忆的信息会沿着时间线向后传播,网络的内部结构如图 1所示。
|
图 1 LSTM结构 Fig. 1 LSTM structure |
LSTM结构包含遗忘门ft、输入门it和输出门ot。ft决定上一时刻细胞状态值Ct-1被遗忘的程度,it则决定记住哪些信息,当前细胞状态值Ct的更新需要ft、it的共同作用,输出层ot根据细胞状态Ct以及输入值Xt来决定最终的输出值ht。每层的输出如下:
| $ {f_t} = \sigma ({W_f} \cdot [{h_{t - 1}}, {X_t}] + {b_f}) $ | (1) |
| $ {i_t} = \sigma ({W_i} \cdot [{h_{t - 1}}, {X_t}] + {b_i}) $ | (2) |
| $ {{\bar C}_t} = {\rm{tanh}}({W_C} \cdot [{h_{t - 1}}, {X_t}] + {b_C}) $ | (3) |
| $ {C_t} = {f_t} \otimes {C_{t - 1}} \otimes {i_t} \otimes {{\bar C}_t} $ | (4) |
| $ {o_t} = \sigma ({W_o} \cdot [{h_{t - 1}}, {X_t}] + {b_o}) $ | (5) |
| $ {h_t} = {o_t} \otimes {\rm{tanh}}({C_t}) $ | (6) |
式中,ht-1为t-1时刻的隐藏层权重,Ct-1为t-1时刻的细胞状态值,σ为Sigmoid激活函数,W、b分别为不同层的权重、偏置值。
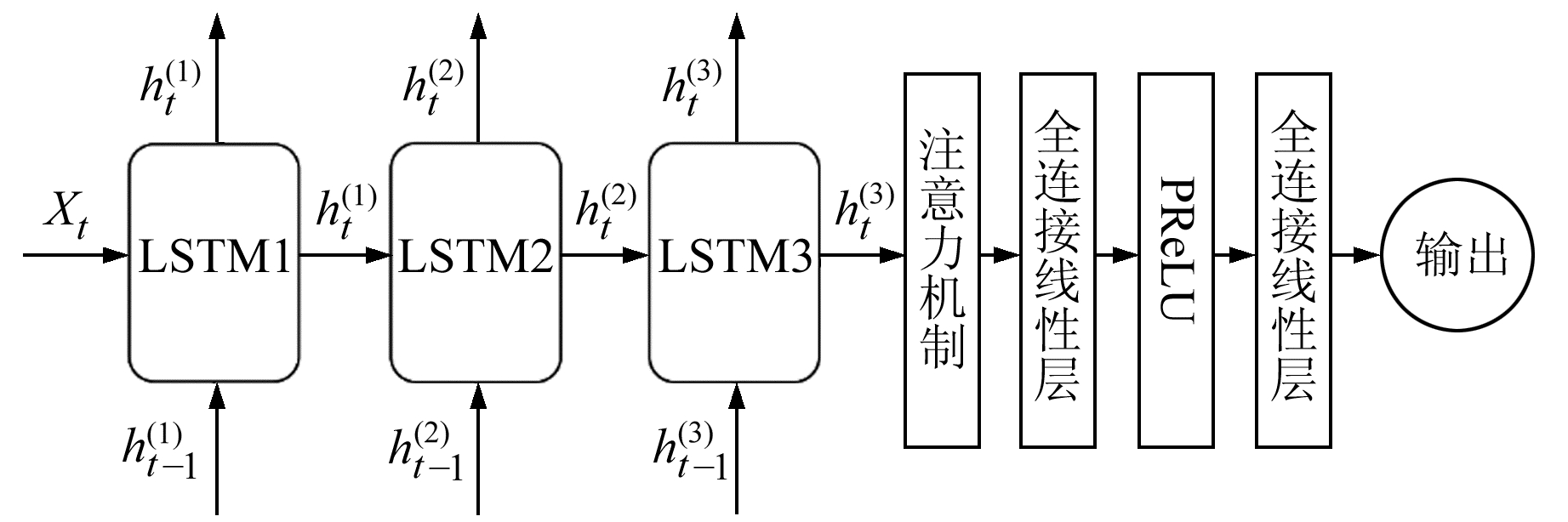
2.2 深度LSTM网络浅度LSTM网络相比于RNN可克服长期依赖的问题,但由于层数较少,难以直观地表示时间序列的复杂特征,特别是处理高度非线性和长时间间隔的数据。从理论上来说,深度和分层的神经网络相比于浅层网络可学习到更高维度、更复杂的特征。从时间轴上来看,RNN是随着时间增加而增加的深度网络,但RNN结构网络仍然可以从输入层-隐藏层、隐藏层-隐藏层、隐藏层-输出层3个方面增加网络层数[20]。本文提出的深度网络结构堆叠多个LSTM以增加隐藏层到隐藏层之间的层数,其目的是使模型在每个循环结构中能够在不同时间尺度上运行并学习不同的特征(图 2)。此外,隐藏层到输出层之间具有深层结构,有助于确定隐藏状态中的变化因素,能够更有效地总结输入历史,从而更容易预测输出。因此,在最后一个LSTM输出层中添加全连接线性层以加深隐藏层到输出层的深度。与BP前馈神经网络类似,RNN结构网络也得益于非饱和激活和Dropout层的使用[21],本文在每层LSTM结构后均添加Dropout层,并在输出层中使用更为先进的PReLU非饱和激活函数[22],以减小过拟合概率。此外,还特别添加注意力(attention)机制[23],以帮助深度网络注意某些重要的长期特征。
|
图 2 深度LSTM网络结构 Fig. 2 Deep LSTM network structure |
图 2为深度LSTM模型结构,将t时刻的输入Xt与前一时刻的隐藏状态ht-1(1)引入到第一个LSTM中。采用§2.1方法计算每个LSTM的隐藏状态输出,ht(1)计算后向上移动至下一个时间步,同时也向右移动至第二个LSTM中,依次类推,直到通过最后一个LSTM并由注意力机制处理,再通过全连接层经PReLU函数激活,最后输出预测数据。
3 模型训练 3.1 训练超参数设置深度LSTM网络训练中的超参数主要为时间间隔步长(预测下一值所用的序列长度)、各LSTM隐藏层神经元数量以及全连接输出层神经元数量。时间序列的统计特性随时间推移会以不可预见的方式变化,若每次输入所有时间序列进行训练相当于增加各种噪声,预测精度会下降,可尝试使用不同的时间步长进行较为准确的预测,因此时间步长也需要作为超参数进行优化。本文采用遗传算法(genetic algorithm, GA)优化网络结构与部分超参数,该算法是借鉴自然进化规律而设计的一种寻找全局最优解的模型,通过群体N代间的不断遗传、交叉、变异来确定问题的最优解。本文实验将LSTM层数分为1、2、3层共3种结构,时间步长为1~12,每层神经元为1~30,每种结构混合不同时间步长和神经元,随机产生40个群体,通过25代遗传进化寻找最优解,最后综合每种结构最优解的评价指标(见§4.1)选取最优模型(表 1)。
|
|
表 1 深度LSTM结构及超参数 Tab. 1 Deep LSTM structure and hyper parameters |
GRACE观测数据中部分月份数据缺失,本文采用三次样条插值法补全缺失的数据。对于明显呈周期特点的时间序列数据,如果采用原始数据进行训练并输出,可能会产生时间平移的现象,这是因为序列存在自相关性,如一阶自相关为当前时刻数值与其自身前一时刻数值之间的相关性。一般可使用差分预测的方式消除自相关性,即通过预测差分值间接预测原始数据值。此外,本文通过插值增大训练数据以减小网络模型的训练难度,在预测后进行降采样得到预测数据。由于LSTM内部采用tanh激活函数,输入数据需归一化到[-1, 1],以避免输入值较大时出现梯度更新较慢的问题。在得到总数据集后,将前157个月作为训练数据,占比85%,其余月份作为测试数据来检验模型的精确性。多次预训练结果表明,当模型初始学习率为10-4、权重优化方法为Adam时,训练效果较好。
4 结果分析 4.1 模型评价指标 4.1.1 均方根误差RMSE均方根误差是一种常用的估计测量方法,可用来表示预测值与实际值之间的差异。当预测值与实际值相同时,该值为0,误差值越大,该值越大。均方根误差值的尺度范围与预测数据一致,因此直接基于该误差的精度测量无法用于不同尺度数据之间的比较。均方根误差表达式为:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n ( {x_i} - {y_i}{)^2}} $ | (7) |
式中,xi为预测值,yi为实际值。
标准化的均方根误差R*,其定义为RMSE与实际值标准差的比值:
| $ {R^*} = \frac{{{\rm{RMSE}}}}{{\sqrt {{\rm{var}}(y)} }} $ | (8) |
NSE系数可以表示模型相对于实际数据平均值的预测能力,可表明实际值与模型预测数据曲线是否符合1 ∶1的线性关系。NSE被认为是评价预测值与观测值整体拟合情况的最佳目标函数[24],可用于对比不同模型对同一数据的拟合优度。NSE系数最佳值为1.0,计算公式为:
| $ {\rm{NSE}} = 1 - \frac{{\sum\limits_{i = 1}^n {{{({x_i} - {y_i})}^2}} }}{{\sum\limits_{i = 1}^n {{{({y_i} - \bar y)}^2}} }} $ | (9) |
式中, y为实际值均值。
本文使用Ahmed等[25]的预测模型的评价标准,将模型性能分为3个主要类别: 1)若NSE大于0.75且R*小于0.50,则性能非常好;2)若NSE大于0.65且R*小于0.60,则性能良好;3)若NSE大于0.65且R*小于0.75,则性能较好。
4.2 结果分析本节将分析深度LSTM网络模型的定量和可视化结果, 所有表格中结果为测试数据所对应模型的性能。模型预测方式有两种:静态更新模式与动态更新模式。在静态模式中,测试数据根据时间步长预测下一数值;在动态模式中,使用预测得到的新值代替测试数据中的实际值来预测下一数值。即得到当前预测值之后,动态模式使用该预测值进行下一序列值预测,而静态模式使用该值对应的实际值进行预测。表 2和表 3分别为深度LSTM模型在动态更新模式下和静态更新模式下各模型评价指标的计算结果,从表中可以看出,静态更新模式的各项指标均优于动态更新模式。动态模式采用预测值进行更新,当前预测值的极小误差会在预测下一序列值时被放大,因此会造成误差积累的现象。
|
|
表 2 动态模式 Tab. 2 Dynamic mode |
|
|
表 3 静态模式 Tab. 3 Static mode |
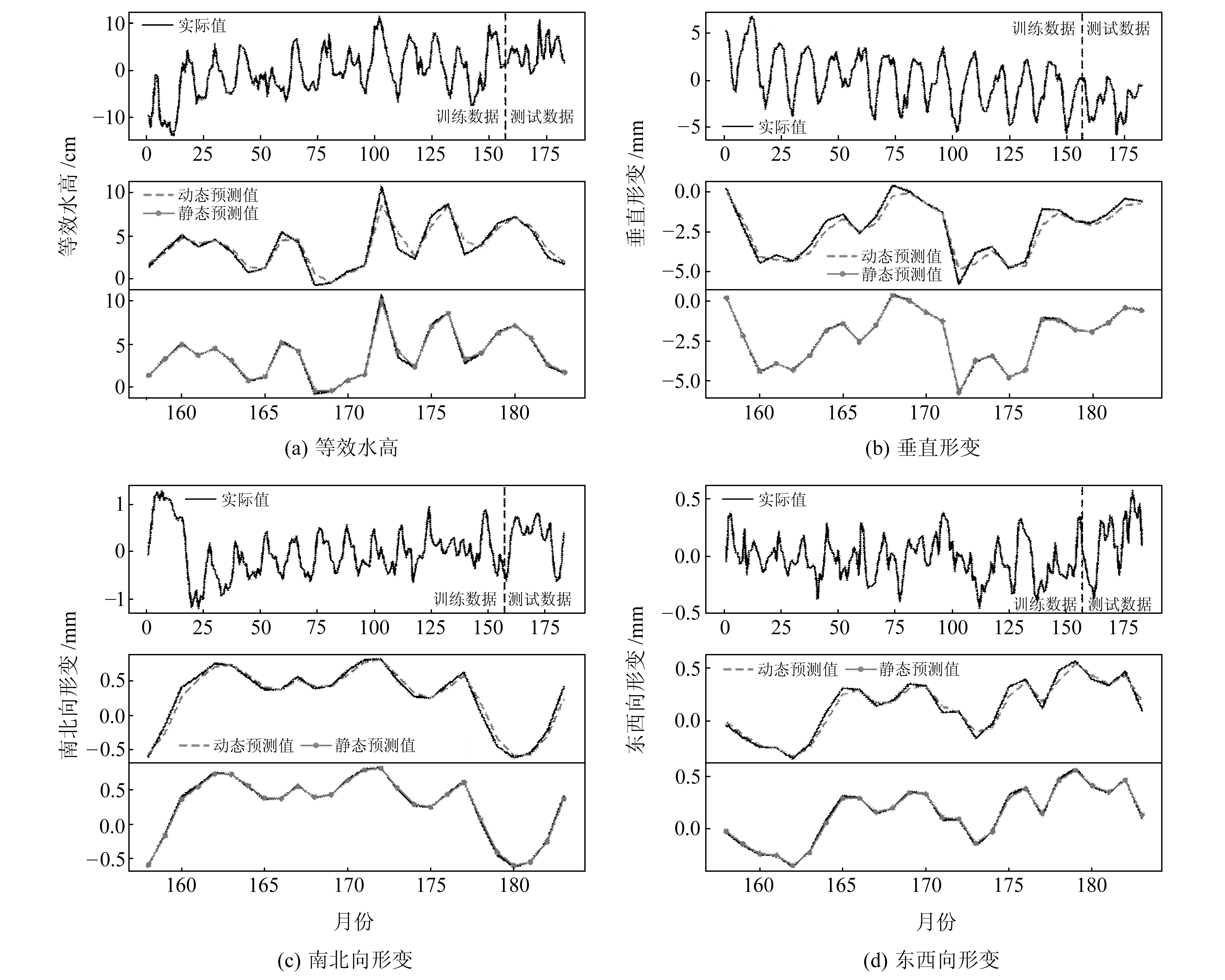
在两种模式中,亚马逊流域各项序列的评价指标R*、NSE均优于长江流域,三峡地区模型表现最差,这是因为三峡地区各项序列本身的复杂程度较高、模型学习难度更大, 但仍优于最佳评价指标。图 3为三峡水库区域等效水高和地表形变量实际值以及在两种不同预测模式下的结果对比,从图中可以看出,静态模式优于动态模式,即使是在动态预测模式下,深度LSTM模型仍具有良好的预测效果。从表 1可以看出,多层LSTM结构为8个,单层LSTM结构为4个,表明深层次的网络结构相对于浅层次更易从复杂序列中分离出时间特征,即深层LSTM网络在时间序列预测方面具有良好效果。
|
图 3 三峡区域预测结果 Fig. 3 Prediction results in the Three Gorges region |
本文使用深度LSTM神经网络预测方法预测GRACE等效水高以及地表垂直方向、水平南北和东西方向位移量。以亚马逊流域、长江流域以及三峡水库作为实验区域,反演2002-04~2017-06 GRACE月时变重力场信息,得到等效水高以及地表位移量月序列值。深度网络模型通过叠加LSTM以及在输出层中添加线性层来增加网络层数,并且在网络中添加注意力机制增加对某些特征的提取能力,同时还利用遗传算法对网络层数、部分超参数进行优化。实验发现,优化后的网络结构对不同地区不同月序列值均具有良好的预测效果。此外, 多层LSTM结构的数量远多于单层,表明深层LSTM网络结构提取复杂特征的能力更强,在时间序列预测上表现优异。
本文对实验序列的处理较为粗糙, 且未考虑气候、地震等因素的影响,因此在具体区域实际应用时需考虑各项因素的影响, 得到精准的时间序列值之后再进行预测。由于GRACE数据中部分月份数据缺失,本文利用三次样条插值法补全缺失值,插值结果并不能完全替代真实值,这可能会模糊部分时间特征。GRACE卫星的继任卫星GRACE-FO(gravity recovery and climate experiment follow-on)已于2018-05升空,将继续执行重力场探测任务,可提供更为丰富的训练数据,深度LSTM网络在这方面的预测结果将会更加精准。
| [1] |
宁津生. 卫星重力探测技术与地球重力场研究[J]. 大地测量与地球动力学, 2002, 22(1): 1-5 (Ning Jinsheng. The Satellite Gravity Surveying Technology and Research of Earth's Gravity Field[J]. Journal of Geodesy and Geodynamics, 2002, 22(1): 1-5)
(  0) 0) |
| [2] |
郑伟, 许厚泽, 钟敏, 等. 地球重力场模型研究进展和现状[J]. 大地测量与地球动力学, 2010, 30(4): 83-91 (Zheng Wei, Xu Houze, Zhong Min, et al. Progress and Present Status of Research on Earth's Gravitational Field Models[J]. Journal of Geodesy and Geodynamics, 2010, 30(4): 83-91)
(  0) 0) |
| [3] |
Frappart F, Papa F, Silva J S, et al. Surface Freshwater Storage and Dynamics in the Amazon Basin during the 2005 Exceptional Drought[J]. Environmental Research Letters, 2012, 7(4): 44 010 DOI:10.1088/1748-9326/7/4/044010
(  0) 0) |
| [4] |
Li S Y, Shen W B, Pan Y J, et al. Surface Seasonal Mass Changes and Vertical Crustal Deformation in North China from GPS and GRACE Measurements[J]. Geodesy and Geodynamics, 2020, 11(1): 46-55 DOI:10.1016/j.geog.2019.05.002
(  0) 0) |
| [5] |
赵少荣, 刘庆元, 朱建军. 联合GPS和GRACE卫星数据反演北美洲的冰川均衡调整模式[J]. 大地测量与地球动力学, 2013, 33(3): 34-40 (Zhao Shaorong, Liu Qingyuan, Zhu Jianjun. Glacial Isostatic Adjustment Models Constrained by Joint Inversion of GPS and GRACE Satellite Observations in North America[J]. Journal of Geodesy and Geodynamics, 2013, 33(3): 34-40)
(  0) 0) |
| [6] |
Bengio Y, Simard P, Frasconi P. Learning Long-Term Dependencies with Gradient Descent is Difficult[J]. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166 DOI:10.1109/72.279181
(  0) 0) |
| [7] |
Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1 735-1 780 DOI:10.1162/neco.1997.9.8.1735
(  0) 0) |
| [8] |
孙宇航, 刘洋. 利用GRU神经网络预测横波速度[J]. 石油地球物理勘探, 2020, 55(3): 484-492 (Sun Yuhang, Liu Yang. Prediction of S-Wave Velocity Based on GRU Neural Network[J]. Oil Geophysical Prospecting, 2020, 55(3): 484-492)
(  0) 0) |
| [9] |
赵勇, 苏丹, 邹丽, 等. 基于LSTM神经网络的畸形波预测[J]. 华中科技大学学报: 自然科学版, 2020, 48(7): 47-51 (Zhao Yong, Su Dan, Zou Li, et al. Rogue Wave Prediction Based on LSTM Neural Network[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2020, 48(7): 47-51)
(  0) 0) |
| [10] |
Shi X J, Chen Z R, Wang H, et al. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting[M]//Cortes C, Lawrence N D, Lee D D, et al. Advances in Neural Information Processing Systems 28. Cambridge: MIT Press, 2015
(  0) 0) |
| [11] |
张建海, 张棋, 许德合, 等. ARIMA-LSTM组合模型在基于SPI干旱预测中的应用——以青海省为例[J]. 干旱区地理, 2020, 43(4): 1 004-1 013 (Zhang Jianhai, Zhang Qi, Xu Dehe, et al. Application of a Combined ARIMA-LSTM Model Based on SPI for the Forecast of Drought: A Case Study in Qinghai Province[J]. Arid Land Geography, 2020, 43(4): 1 004-1 013)
(  0) 0) |
| [12] |
殷兆凯, 廖卫红, 王若佳, 等. 基于长短时记忆神经网络(LSTM)的降雨径流模拟及预报[J]. 南水北调与水利科技, 2019, 17(6): 1-9 (Yin Zhaokai, Liao Weihong, Wang Ruojia, et al. Rainfall-Runoff Modelling and Forecasting Based on Long Short-Term Memory(LSTM)[J]. South-to-North Water Transfers and Water Science and Technology, 2019, 17(6): 1-9)
(  0) 0) |
| [13] |
王国松, 王喜冬, 侯敏, 等. 基于观测和再分析数据的LSTM深度神经网络沿海风速预报应用研究[J]. 海洋学报, 2020, 42(1): 67-77 (Wang Guosong, Wang Xidong, Hou Min, et al. Research on Application of LSTM Deep Neural Network on Historical Observation Data and Reanalysis Data for Sea Surface Wind Speed Forecasting[J]. Acta Oceanologica Sinica, 2020, 42(1): 67-77 DOI:10.3969/j.issn.0253-4193.2020.01.008)
(  0) 0) |
| [14] |
Cheng M K, Tapley B D, Ries J C. Deceleration in the Earth's Oblateness[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(2): 740-747 DOI:10.1002/jgrb.50058
(  0) 0) |
| [15] |
Swenson S, Chambers D, Wahr J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B8)
(  0) 0) |
| [16] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B12): 30 205-30 229 DOI:10.1029/98JB02844
(  0) 0) |
| [17] |
Chen J L, Wilson C R, Li J, et al. Reducing Leakage Error in GRACE-Observed Long-Term Ice Mass Change: A Case Study in West Antarctica[J]. Journal of Geodesy, 2015, 89(9): 925-940 DOI:10.1007/s00190-015-0824-2
(  0) 0) |
| [18] |
Swenson S, Wahr J. Methods for Inferring Regional Surface-Mass Anomalies from Gravity Recovery and Climate Experiment(GRACE) Measurements of Time-Variable Gravity[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B9)
(  0) 0) |
| [19] |
Kusche J, Schrama E J O. Surface Mass Redistribution Inversion from Global GPS Deformation and Gravity Recovery and Climate Experiment (GRACE) Gravity Data[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B9)
(  0) 0) |
| [20] |
Pascanu R, Gulcehre C, Cho K, et al. How to Construct Deep Recurrent Neural Networks[C]. International Conference on Learning Representations, Banff, 2014
(  0) 0) |
| [21] |
Bayer J, Osendorfer C, Korhammer D, et al. On Fast Dropout and Its Applicability to Recurrent Networks[EB/OL]. 2013
(  0) 0) |
| [22] |
He K M, Zhang X Y, Ren S Q, et al. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification[C]. IEEE International Conference on Computer Vision, Santiago, 2015
(  0) 0) |
| [23] |
Vaswani A, Shazeer N, Parmar N, et al. Attention Is All You Need[C]. 31st Conference on Neural Information Processing Systems, Long Beach, 2017
(  0) 0) |
| [24] |
Servat E, Dezetter A. Selection of Calibration Objective Fonctions in the Context of Rainfall-Ronoff Modelling in a Sudanese Savannah Area[J]. Hydrological Sciences Journal, 1991, 36(4): 307-330 DOI:10.1080/02626669109492517
(  0) 0) |
| [25] |
Ahmed M, Sultan M, Elbayoumi T, et al. Forecasting GRACE Data over the African Watersheds Using Artificial Neural Networks[J]. Remote Sensing, 2019, 11(15): 1 769 DOI:10.3390/rs11151769
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


