2. 中国测绘科学研究院, 北京市莲花池西路28号, 100830
GRACE时变重力场在区域水负荷形变监测方面已取得重要进展,特别是在华北地区,不同深度含水层地下水的减少会对地面产生形变影响[1-2],该问题已引发国内学者高度关注。此外,对于冰川均衡调整(glacial isostatic adjustment, GIA)效应、气候变化引起的固体地球负荷形变等,GRACE也可实现有效监测[3],如南格陵兰岛冰盖消融引起的地面回弹[4]、云南地区大幅降水导致的地表位移以及La Niña事件与水循环引起的澳大利亚大陆弹性形变等[5]。
真实地壳存在分层性与粘滞性,但在地壳负荷形变模拟和理论计算时,通常可忽略该项影响,从而把真实地球简化成各向同性的理想弹性地球模型,采用表征球或椭球的几何参数,如几何形状、密度、拉梅常数等进行描述[6]。目前常用的地球模型有PREM、SNREI和Gutenberg-Bullen A,这3种地球模型计算得到的负荷勒夫数的一致性可达到1%[7-8]。在目前利用GRACE重力卫星反演地表负荷垂直形变的计算中,一般采用基于PREM地球模型得到的负荷勒夫数,但该模型使用的弹性结构参数无法很好地凸显中国大陆的地球结构[9]。PREM地球模型使用国际地震学收集的1964~1975年的体波传播时间和正常模式的数据,该模型自1981年被提出以来,已被广泛用于研究海洋潮汐、陆地水变化、冰融化和末级冰川作用的负荷响应。此外,随着地壳深度方向分辨率的提升,虽然Crust2.0已产生新的地壳弹性结构,但在模型建模过程中未被加载[10]。
GRACE-FO卫星于2018-05成功发射,将延续GRACE的科学计划,有望在水文大地测量学等领域发挥巨大作用。因此,本文利用GRACE-FO卫星数据估算近10个月陆地水负荷垂直形变。为定量研究区域地壳结构差异对GRACE-FO数据估算中国大陆地表垂直负荷形变的影响,本文对比分析PREM、含中国大陆地球结构的Hard-PREM与Soft-PREM三种地球模型的负荷勒夫数,计算每两者之间负荷勒夫数的差异,并对差异最大的负荷勒夫数进行应用分析,同时与PREM模型的结果进行比较,以反映地壳结构差异对新一代卫星重力估算结果的影响。
1 数据与方法 1.1 数据GRACE-FO项目发布的第一个RL06 Level-2数据产品包含JPL、GFZ、CSR的10个月重力场观测数据,以及相应的大气和海洋预处理(AOD)背景模型数据,包括GAC、GAD、GSM,其中2018-08、09数据缺失。月值二级产品于2019-07开始每月在PO.DAAC和ISDC更新发布,包含60阶与90阶球谐重力位系数,下载网址为https://podaac-tools.jpl.nasa.gov/drive/files/allData/gracefo。本文采用2018-06~2019-05的RL06 Level-2 GSM大地水准面球谐系数进行研究。GRACE-FO作为GRACE卫星重力测量的延续,在微波测距、距离变率、AOD背景场以及ACC、KBR、GNSS、SCA测量仪器等方面均与GRACE相同。
1.2 方法地表质量变化通常用等效水高变化来表示,等效水高可表示为Δh(θ, λ)=Δσ(θ, λ)/ρw:
| $ \begin{array}{l} \;\;\Delta h(\theta , \lambda ) = \frac{{a{\rho _e}}}{{3{\rho _w}}}\sum\limits_{n = 0}^\infty {\sum\limits_{m = 0}^n {\frac{{2n + 1}}{{1 + {k_n}}}} } \cdot \\ \left[ {\Delta {C_{nm}}\cos (m\lambda ) + \Delta {S_{nm}}\sin (m\lambda )} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\bar P}_{nm}}(\cos \theta ) \end{array} $ | (1) |
式(1)为时变重力场的基本方程之一,kn为位勒夫数。为减小GRACE高阶噪声的影响,需采用滤波方法进行抑制[11-13]。
地表质量变化引起的地球弹性负荷垂直形变可表示为[3]:
| $ {\mathop{\rm Vertical}\nolimits} (\varphi , \lambda ) = \frac{3}{{{\rho _e}}}\sum\limits_{n = 0}^\infty {\frac{{h{'_n}}}{{2n + 1}}} \cdot {Q_n}(\varphi , \lambda ) $ | (2) |
| $ \begin{array}{l} {Q_n}(\varphi , \lambda ) = \sum\limits_{m = 0}^n {\left[ {Q_{n, m}^c(\varphi , \lambda )\cos (m\lambda ) + } \right.} \\ \;\;\;\;\left. {Q_{n, m}^s(\varphi , \lambda )\sin (m\lambda )} \right] \cdot {P_{n, m}}(\sin \varphi ) \end{array} $ | (3) |
式中,φ、λ为计算点的余纬、经度,θ为待求计算点(φ, λ)到负荷点源之间的空间角距,h′n为径向负荷勒夫数,Qn(φ, λ)为球谐展开形式的负荷值,Qn, mc、Qn, ms为球谐展开的n阶m次斯托克斯系数,ρe为地球密度,Pn, m为缔合勒让德函数。
本文采用的负荷勒夫数基于PREM模型获得,与文献[14]相同,其阶次高达40 000。
2 我国陆地水储量近10个月时空变化特征GRACE-FO重力卫星可为研究我国陆地水质量迁移提供新型数据支持,本文采用3家机构的GRACE-FO卫星时变重力场模型研究2018-06~2019-05期间我国陆地水储量的时空变化特征,并对国际上不同机构发布的GRACE-FO时变重力场模型进行比较分析。
对60阶GSM数据进行预处理,GRACE-FO的GSM球谐数据预处理过程与GRACE类似,一阶项与C20替换文件均可从网址https://podaac-tools.jpl.nasa.gov下载。SLR提供的与GRACE-FO时间匹配的C20序列,可同时用于3家机构数据的替换;但对于一阶项,每个机构均有各自的替换文件,3家机构的一阶项球谐系数均由Jet Propulsion Laboratory(JPL)实验室按照各自机构的解算方法以及不同的数据处理策略进一步解算得到。采用相同的时间基准,获得相对于同一基准下GRACE-FO大地水准面球谐系数变化量。为减小重力场模型中的条带误差,采用组合滤波方法去除条带。
滤波平滑过程在降低重力场模型高阶项噪声影响的同时,不可避免会引起区域信号混叠与振幅衰减[15]。针对大尺度区域的陆地水反演,本文采用正向建模方法[16]对3家机构反演的陆地水储量变化进行泄漏误差改正。图 1、2分别为2018年、2019年3家机构GRACE-FO数据反演的陆地水储量变化。

|
图 1 2018年CSR、GFZ、JPL的GRACE-FO数据反演的陆地水储量变化 Fig. 1 TWS changes derived from GRACE-FO data from CSR, GFZ and JPL in 2018 |

|
图 2 2019年CSR、GFZ、JPL的GRACE-FO数据反演的陆地水储量变化 Fig. 2 TWS changes derived from GRACE-FO data from CSR, GFZ and JPL in 2019 |
从图 1、2可以看出,3家机构的反演结果都能较好地表征我国陆地水在2018-06~2019-05的时空变化信息,时空变化趋势整体具有很强的一致性。2018年下半年,我国陆地水变化最大幅值为±25 cm,陆地水空间分布具有明显的不均匀性。特别是在7月,长江沿线地区陆地水储量相比其他地区明显增多,陆地水整体以正变化为主;10月云南地区水储量增幅达到25 cm,而湖南和江西一带出现明显负异常,幅值为-25 cm;11月和12月,这两处质量集中的区域其信号强度均逐渐减弱。2019年上半年,我国陆地水储量变化幅值在-25~10 cm范围内,水储量增长幅度相比于2018年下半年有所放缓;2019-01~05云南地区与湖南和江西一带仍然出现正负异常的水文信号,同时质量逐渐累积,在5月达到上半年的最大幅值。此外,山东地区水储量也呈现由小幅盈余逐月减小至轻微亏损;青藏高原地区表现出陆地水质量随时间的迁移与再分布特征。
除具有很大程度的时空共性外,3家机构的反演结果在局部地区仍存在细微差别,主要体现在信号的变化幅值上。从图 1、2可以明显看出,2018-06黑龙江地区水储量处于减少状态,其中GFZ结果减少幅度最大,其次为JPL,CSR结果的信号强度最不明显。2018-10新疆地区西北部水储量信号表现为负异常,相比于JPL和CSR,GFZ结果特征最为显著。这些微小差异可能源自重力卫星观测数据在进行重力场模型解算时采用的轨道动力学模型之间的细微差别。
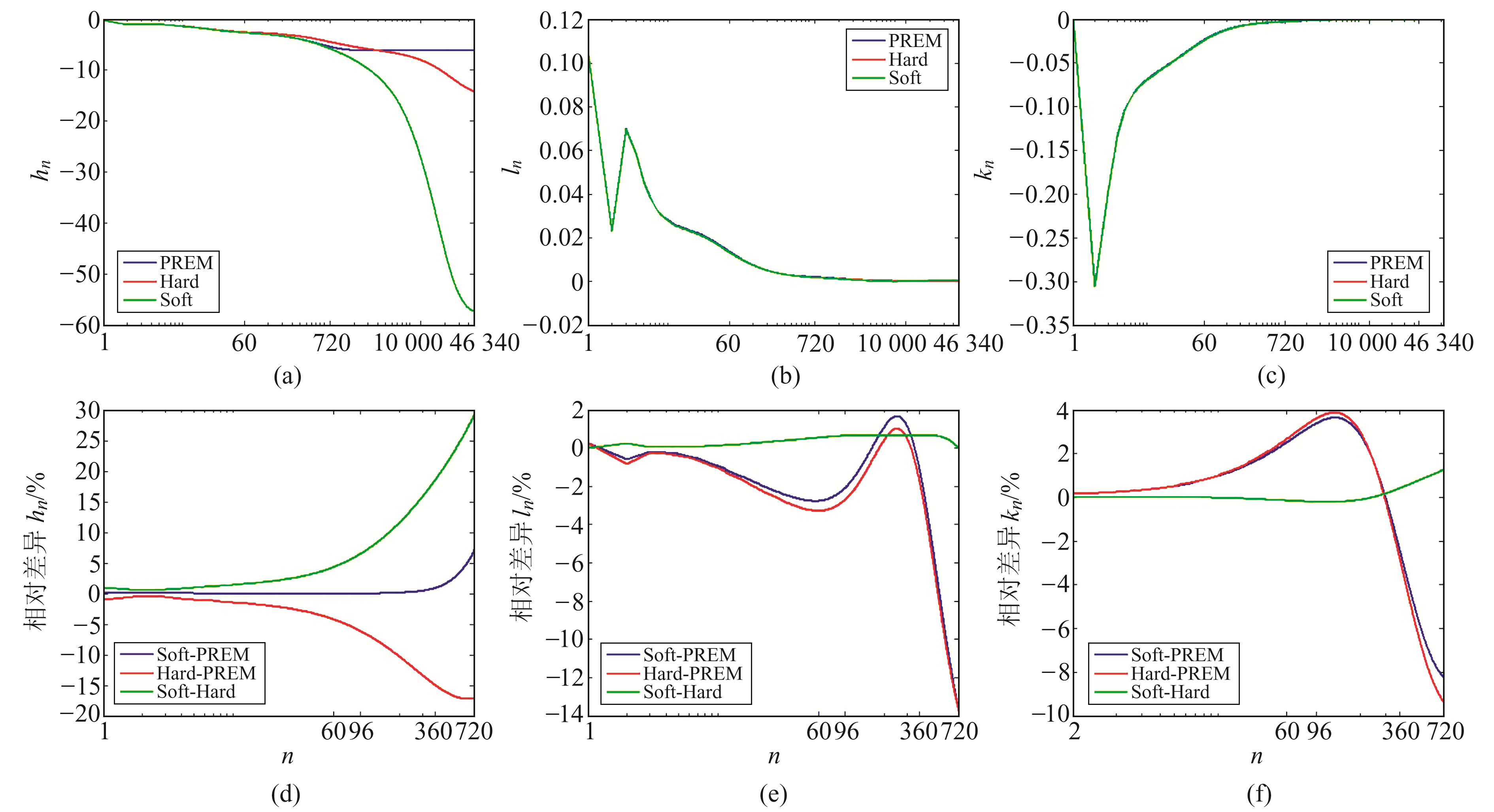
3 不同地球模型负荷勒夫数对比分析针对PREM模型及由此模型计算的负荷勒夫数不能较好地反映中国大陆地壳结构的问题,本文进一步采用Wang等[14]改进的M-PREM模型探讨地壳结构差异对GRACE-FO估算中国大陆地壳垂直负荷形变的影响。为研究这种差异的影响,Wang等[14]将Crust2.0地球结构最外层细分成软、硬沉积物层,相关的改进模型被称为“软”和“硬”模型,即Soft和Hard模型。根据PREM、Hard、Soft模型分别解算的径向位移负荷勒夫数、水平位移负荷勒夫数、位负荷勒夫数如图 3(a)~(c)所示。
|
图 3 PREM、Hard、Soft模型对应的LLNs及其相对差异 Fig. 3 LLNs corresponding to PREM, Hard and Soft models and relative differences |
Soft和Hard模型的地壳最外层相比于PREM模型均较软,Soft模型相比于Hard模型也较软,该差异会对高阶负荷勒夫数结果产生影响。从图 3(a)~(c)可以看出,Soft和Hard模型的径向负荷勒夫数在阶数大于720时,与PREM模型的差异较明显,随着阶数增加,差异也随之增大。相比之下,3个模型之间的水平位移负荷勒夫数、位负荷勒夫数的绝对差异较小。为更加清晰地比较3个模型负荷勒夫数之间的差异,基于上述不同模型所得到的负荷勒夫数,计算其相对差异,结果如图 3(d)~(f)所示。从图中可以看出,径向负荷勒夫数随着阶数增加,Soft与PREM模型的相对差异基本在0值上下浮动,而Hard与PREM模型的相对差异逐渐偏离0值;当阶数大于60时,偏离幅值呈发散式放大。水平位移负荷勒夫数随着阶数增加,Soft与PREM模型以及Hard与PREM模型的相对差异曲线均表现出较为一致的波动变化。3种模型的位负荷勒夫数的相对差异也均呈现出高度一致的起伏特征。表明Soft和Hard模型对应的水平位移负荷勒夫数与位负荷勒夫数无明显差异,而径向负荷勒夫数差异最为显著。
上述分析表明,Hard/Soft-PREM地球模型的水平位移负荷勒夫数和位负荷勒夫数与PREM模型的相对偏差很小,因此本文重点分析Hard/Soft-PREM模型对应的径向负荷勒夫数与PREM模型的差异(表 1)。
|
|
表 1 Soft和Hard模型对应的径向负荷勒夫数hn与PREM模型的相对差异 Tab. 1 The relative differences between radial LLNs hn from Soft, Hard and PREM models |
从表 1可以看出,当阶数为60时,Soft、Hard与PREM模型径向负荷勒夫数的相对偏差达到-0.132%、-4.267%,Soft与Hard模型径向负荷勒夫数的相对偏差达到4.32%。在高阶项720阶,Soft、Hard与PREM模型径向负荷勒夫数的相对偏差增加数倍,达到6.865%、-17.18%,Soft与Hard模型径向负荷勒夫数的相对偏差达到29.03%。相比于Soft模型,Hard与PREM模型径向负荷勒夫数的相对差异更为显著。
因此,本文重点关注Hard与PREM模型的差异对前60阶径向负荷勒夫数的影响,两者径向负荷勒夫数在60阶时相对差异为-4.267%,60阶之前呈现负增长趋势,随着阶数递增相对差异也随之增大,这对利用GRACE-FO数据估算中国陆地水负荷垂直形变可能会产生较大影响。
4 GRACE-FO估算地表垂直负荷形变特征分析为定量分析Hard与PREM模型的差异对GRACE-FO估算地表垂直负荷形变的影响,本文采用CSR发布的GRACE-FO卫星2018-06~2019-05的RL06数据(2018-08、09缺失),球谐系数为60阶,该数据主要体现陆地水质量变化信号。GRACE-FO重力场模型的预处理过程与前文相同。
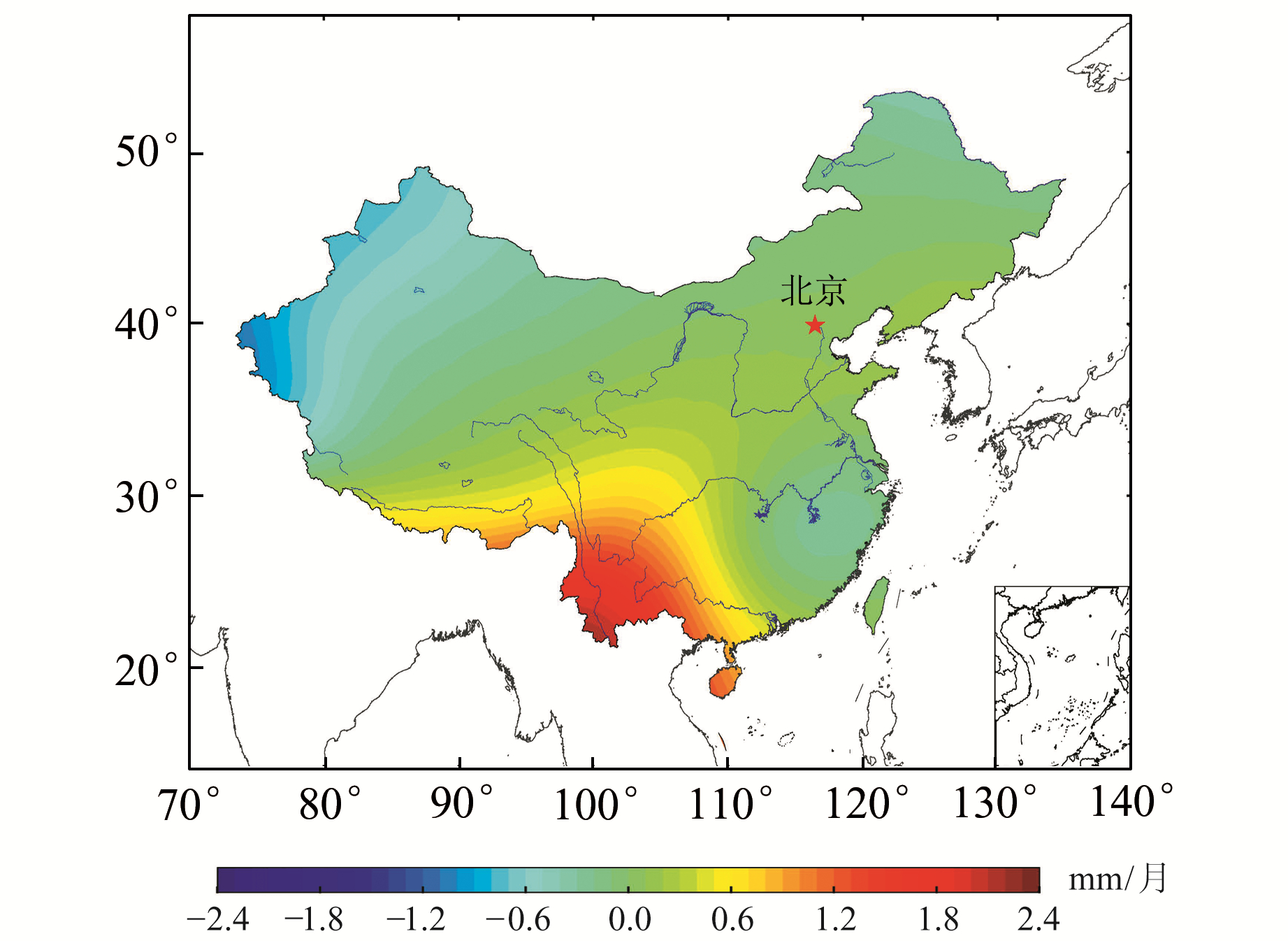
根据计算公式得到中国大陆垂直负荷形变的格网时间序列,通过一元线性回归分析方法计算GRACE-FO估算的前60阶垂直负荷形变线性速率分布,图 4为基于60阶Hard模型得到的结果。根据地球弹性负荷理论,图 4中垂直负荷形变速率为正值表示在监测时段内陆地水质量呈减少趋势(单位mm/月),而负值则表示陆地水质量呈增加趋势,主要反映气候驱动与人为因素综合影响下陆地水质量的分布状态。GRACE-FO估算的地表垂直负荷形变速率在各地区存在差异,总体来说,中国北方的垂直速率一般较小,而南方垂直速率较大,正速率最大值位于云南一带的澜沧江-金沙江-南盘江并流区,每月达到约2.4 mm的正变化,在长江流经区域的江西和湖南一带也呈现出地表逐月微弱下沉的趋势,约为-0.624 mm/月。
|
图 4 基于60阶Hard模型得到的陆地水负荷垂直形变的线性趋势 Fig. 4 Linear trend of vertical deformation of terrestrial water load based on 60-order Hard model |
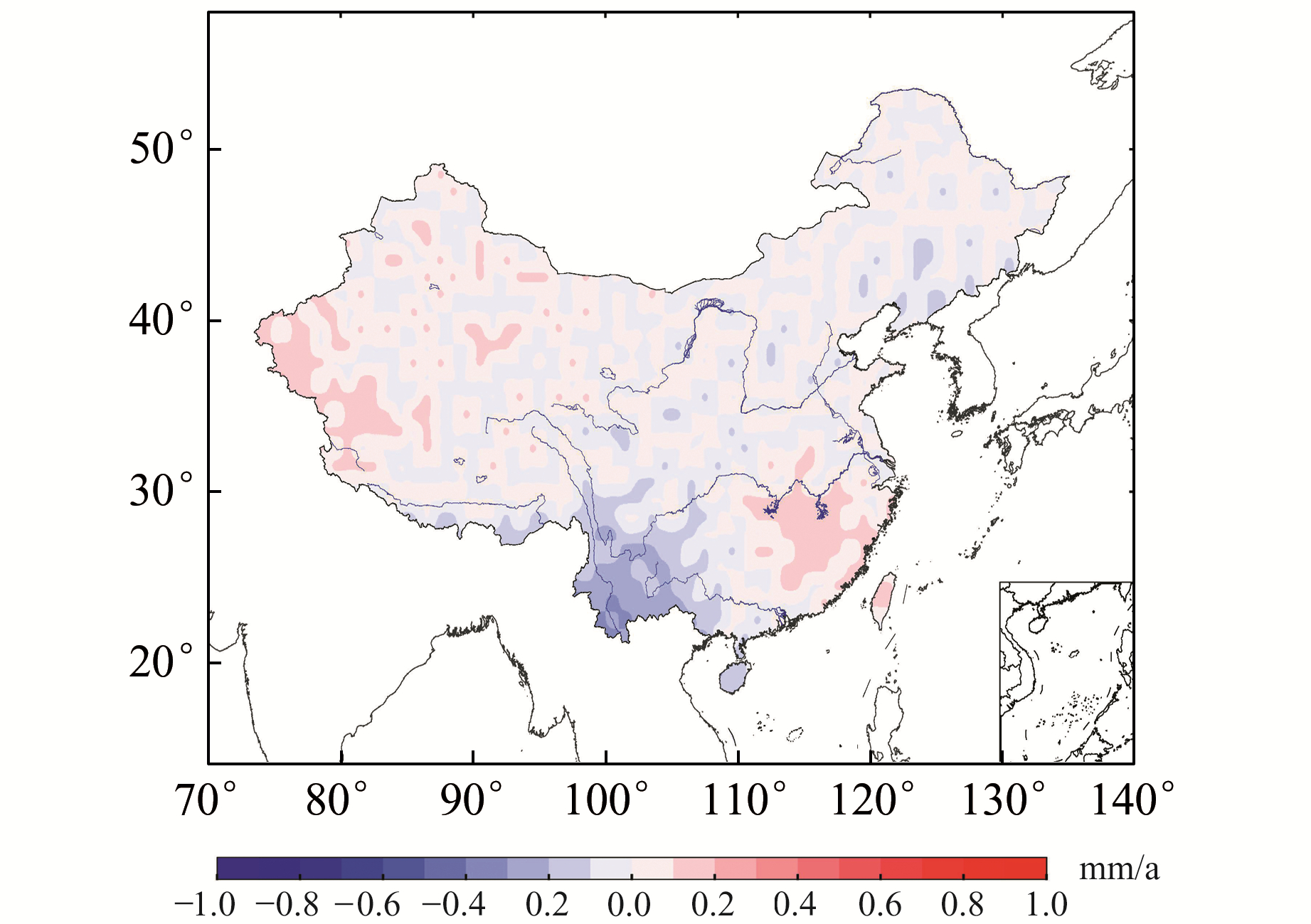
为进一步探讨区域地球结构的影响,采用PREM模型的负荷勒夫数计算研究区地表负荷形变速率,进一步分析两种不同地球结构模型的差异,结果如图 5所示。从图 5可以看出,基于两种不同地壳结构模型的地表垂直负荷形变差异相对较大,最大差异位于云南一带的澜沧江流域地区,幅值约为0.7 mm/a;湖南和江西地区其模型差异的幅值约为0.5 mm/a;新疆西南部地球结构模型的结果差异也较大,以0.5 mm/a为主。云南一带的澜沧江流域地区地质构造活动较明显且陆地水变化较为显著,这可能是引起地表垂直形变的重要因素,而Hard模型相比于PREM模型包含了不同的地球物理参数,更能体现该区域地壳结构特征,因此两种地球模型在该区域会表现出较大的地表垂直负荷形变差异。
|
图 5 Hard模型与PREM模型估算地表垂直负荷形变线性速率的差异 Fig. 5 Difference of linear rate of vertical defomation using Hard and PREM model |
本文主要探讨利用Hard与PREM模型分析区域地球结构差异对前60阶径向负荷勒夫数估算陆地水负荷垂直形变的影响。研究结果表明,径向负荷勒夫数在60阶时相对差异为-4.267%,60阶之前呈现负增长趋势,随着阶数递增相对差异也随之增大,这对利用GRACE-FO数据估算中国陆地水负荷垂直形变可能会产生较大影响。GRACE-FO估算的地表垂直负荷形变速率大小因地而异,中国北方的垂直速率一般较小,而南方垂直速率较大,正速率最大值位于云南一带的澜沧江-金沙江-南盘江并流区,每月达到约2.4 mm的正变化,在长江流经区域的江西和湖南一带也呈现出地表逐月微弱下沉的趋势,约为-0.624 mm/月。两种不同地壳结构模型的地表垂直负荷形变差异相对较大,最大差异位于云南一带的澜沧江流域地区,幅值约为0.7 mm/a;湖南和江西地区其模型差异的幅值约为0.5 mm/a;新疆西南部地壳结构模型的结果差异也较大,以0.5 mm/a为主。因此,在使用GRACE-FO重力卫星数据估算中国大陆地表垂直负荷形变时,区域地球结构的影响不容忽视。
| [1] |
Wang L S, Chen C, Du J S, et al. Detecting Seasonal and Long-Term Vertical Displacement in the North China Plain Using GRACE and GPS[J]. Hydrology and Earth System Sciences, 2017, 21(6): 2905-2922 DOI:10.5194/hess-21-2905-2017
(  0) 0) |
| [2] |
Liu R L, Zou R, Li J C, et al. Vertical Displacements Driven by Groundwater Storage Changes in the North China Plain Detected by GPS Observations[J]. Remote Sensing, 2018, 10(2): 259 DOI:10.3390/rs10020259
(  0) 0) |
| [3] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797 DOI:10.1029/RG010i003p00761
(  0) 0) |
| [4] |
贾路路, 汪汉胜, 相龙伟, 等. 冰川均衡调整对南极冰质量平衡监测的影响及其不确定性[J]. 地球物理学报, 2011, 54(6): 1466-1477 (Jia Lulu, Wang Hansheng, Xiang Longwei, et al. Effects of Glacial Isostatic Adjustment on the Estimate of Ice Mass Balance over Antarctica and the Uncertainties[J]. Chinese Journal of Geophysics, 2011, 54(6): 1466-1477 DOI:10.3969/j.issn.0001-5733.2011.06.006)
(  0) 0) |
| [5] |
Wang S Y, Chen J L, Wilson C R, et al. Reconciling GRACE and GPS Estimates of Long-Term Load Deformation in Southern Greenland[J]. Geophysical Journal International, 2018, 212(2): 1302-1313 DOI:10.1093/gji/ggx473
(  0) 0) |
| [6] |
Fu Y N, Freymueller J T. Seasonal and Long-Term Vertical Deformation in the Nepal Himalaya Constrained by GPS and GRACE Measurements[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B3)
(  0) 0) |
| [7] |
Dziewonski A M, Anderson D L. Preliminary Reference Earth Model[J]. Physics of the Earth and Planetary Interiors, 1981, 25(4): 297-356 DOI:10.1016/0031-9201(81)90046-7
(  0) 0) |
| [8] |
汪汉胜, 许厚泽, 李国营. SNREI地球模型负荷勒夫数数值计算的新进展[J]. 地球物理学报, 1996, 39(增): 182-189 (Wang Hansheng, Xu Houze, Li Guoying. Improvement of Computations of Load Love Numbers of SNREI Earth Model[J]. Chinese Journal of Geophysics, 1996, 39(S): 182-189)
(  0) 0) |
| [9] |
Wang H S, Xiang L W, Wu P, et al. Effects of the Tibetan Plateau Crustal Structure on the Inversion of Water Trend Rates Using Simulated GRACE/GPS Data[J]. Terrestrial Atmospheric and Oceanic Sciences, 2013, 24(4): 505-512
(  0) 0) |
| [10] |
贾路路, 相龙伟, 汪汉胜. 地壳结构对GRACE估算中国大陆地表垂直负荷形变的影响[J]. 地球科学进展, 2014, 29(7): 828-834 (Jia Lulu, Xiang Longwei, Wang Hansheng. Effects of Crustal Structure for Estimation of Vertical Load Deformation on the Solid Earth Using GRACE in China Mainland[J]. Advances in Earth Science, 2014, 29(7): 828-834)
(  0) 0) |
| [11] |
Han S C, Shum C K, Jekeli C, et al. Non-Isotropic Filtering of GRACE Temporal Gravity for Geophysical Signal Enhancement[J]. Geophysical Journal International, 2005, 163(1): 18-25 DOI:10.1111/j.1365-246X.2005.02756.x
(  0) 0) |
| [12] |
Zhang Z Z, Chao B F, Lu Y, et al. An Effective Filtering for GRACE Time-Variable Gravity: Fan Filter[J]. Geophysical Research Letters, 2009, 36(17)
(  0) 0) |
| [13] |
詹金刚, 王勇, 郝晓光. GRACE时变重力位系数误差的改进去相关算法[J]. 测绘学报, 2011, 40(4): 442-446 (Zhan Jingang, Wang Yong, Hao Xiaoguang. Improved Method for Removal of Correlated Errors in GRACE Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 442-446)
(  0) 0) |
| [14] |
Wang H S, Xiang L W, Jia L L, et al. Load Love Numbers and Green's Functions for Elastic Earth Models PREM, Iasp91, Ak135, and Modified Models with Refined Crustal Structure from Crust2.0[J]. Computers and Geosciences, 2012, 49: 190-199 DOI:10.1016/j.cageo.2012.06.022
(  0) 0) |
| [15] |
Zhong Y L, Zhong M, Mao Y N, et al. Evaluation of Evapotranspiration for Exorheic Catchments of China during the GRACE Era: From a Water Balance Perspective[J]. Remote Sensing, 2020, 12(3): 511 DOI:10.3390/rs12030511
(  0) 0) |
| [16] |
Chen J L, Wilson C R, Famiglietti J S, et al. Spatial Sensitivity of the Gravity Recovery and Climate Experiment (GRACE) Time-Variable Gravity Observations[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B8)
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China
 2021, Vol. 41
2021, Vol. 41


