2. 苏州科技大学北斗导航与环境感知研究中心,苏州市学府路99号,215009;
3. 江苏省气象科学研究所,南京市昆仑路16号,210009
水汽是大气中最活跃的成分,精确测量大气中水汽及其变化趋势对研究天气变化、预报天气具有重要意义[1]。PWV是衡量大气中水汽含量的重要指标之一。GPT系列模型不受实测数据限制、使用方便且适用范围广,能够提供反演PWV所必需的气压、温度等气象参数,是获取高精度PWV和进行短期降水预报的有效方法之一[2-6]。
本文利用2017年长三角地区7个探空站和2个GNSS站的实测数据,对GPT2w模型的主要经验气象元素(气压、温度和水汽压等)和ZTD精度进行验证,并评价其在长三角地区的适用性。针对GPT2w模型获取的ZTD精度较差的问题,本文将融合GNSS-ZTD与基于GPT2w模型获取的气象参数,以期改善PWV反演精度。
1 GPT2w模型GPT2w模型只需提供测站大地坐标(B、L、H)和年积日(doy)即可输出全球任意位置所需参数值(http://ggosatm.hg.tuwien.ac.at/DELAY/SOURCE/GPT2w/),计算公式为[2]:
| $ \begin{array}{l} {W_p} = {\alpha _0} + {\alpha _1}\cos \left( {2\pi \frac{{{\rm{ doy }}}}{{365.25}}} \right) + {\beta _1}\sin \left( {2\pi \frac{{{\rm{ doy }}}}{{365.25}}} \right) + \\ \;\;\;\;\;\;{\alpha _2}\cos \left( {4\pi \frac{{{\rm{ doy }}}}{{365.25}}} \right) + {\beta _2}\sin \left( {4\pi \frac{{{\rm{ doy }}}}{{365.25}}} \right) \end{array} $ | (1) |
式中,Wp为格网点处气压、温度、水汽压和Tm等气象参数值,α0为平均值,(α1,β1)为年周期振幅,(α2,β2)为半年周期振幅,这些模型系数可结合外部格网文件gpt2_1w.grd和测站坐标,采用双线性内插法获得。
式(1)得到的气象参数为格网点处数据,不同高度测得的数据可由式(2)获得:
| $ \left\{ {\begin{array}{*{20}{l}} {T = {T_0} + {\rm{d}}T(K) \times h \times 1000 - 273.15}\\ {P = {P_0} \times e\left\{ { - {g_m} \times \frac{{{\rm{d}}{{\rm{M}}_{tr}}}}{{\left[ {{R_g} \times {T_0} \times (1 + 0.6077Q)} \right]}} \times {\rm{dh}}} \right\}/100}\\ {{e_0} = Q \times \frac{{{P_0}}}{{(0.622 + 0.3780Q)}}/100}\\ {e = {e_0} \times {{\left( {100 \times P/{P_0}} \right)}^{(\lambda + 1)}}} \end{array}} \right. $ | (2) |
式中,P0、T0、e0分别为格网点处气压(单位hPa)、温度(单位℃)、水汽压(单位hPa),dT为温度递减率(单位K/km),h为高度(单位m),P、T、e为格网点处对应高度为h时的气压、温度和水汽压,gm为重力(单位m/s2),dMtr为干空气摩尔质量(单位kg/mol),Rg为气体常数(单位J/(K ·mol)),Q为比湿(单位g/kg),λ为水汽压垂直梯度,本文取gm=9.806 65 m/s2,dMtr=28.965×10-3 kg/mol,Rg=8.314 3 J/(K ·mol),Q与λ均可通过式(1)获得。
一般而言,探空站的ZHD可由Saastamoinen模型获得:
| $ {\rm{ ZHD }} = \frac{{0.0022768P}}{{1 - 0.00266\cos (2\varphi ) - 0.00000028H}} $ | (3) |
式中,φ为站点纬度(单位rad),H为测站高程(单位m)。GPT2w模型计算ZWD可由Askne-Nordius模型得到:
| $ {\rm{ZWD}} = {10^{ - 6}}\left( {k{'_2} + {k_3}/{T_m}} \right)\frac{{{R_d}}}{{(\lambda + 1){g_m}}}e $ | (4) |
式中,k′2、k3及Rd均为模型中的经验常数,本文取k3=3.776×105 K2/hPa,k′2=k2-k1×(mv/md) K/hPa,k1=77.604,k2=64.79,mv=18.015 2,md=28.964 4,Rd=287.054 J/(kg ·K)。
2 数据来源及处理方法 2.1 数据来源本文数据主要来自2017年长三角地区7个探空站(http://weather.uwyo.edu/upperair/sounding.html)和2个GNSS基准站,探空资料时间分辨率为12 h,每天08:00和20:00各采集1次,包括不同高度的实测温度、气压和露点温度等气象参数及大气水汽含量、位置参数等地面信息。探空站实测数据主要用来对比气压、温度和水汽压等气象参数及Tm精度,GNSS数据用来对比GPT2w模型ZTD精度。图 1和表 1为长三角地区7个探空站和2个GNSS站的位置信息,其中射阳站的GNSS基准站与探空站经纬度一致,安庆站的GNSS基准站与探空站位置相近,实际相距约10 km,对计算PWV影响较小,可用于PWV精度验证。

|
图 1 探空站和GNSS站分布 Fig. 1 Distribution of radiosonde stations and GNSS stations |
|
|
表 1 长三角地区探空站和GNSS站信息 Tab. 1 Information of radiosonde stations and GNSS stations in Yangtze River delta |
将探空站测得的气象参数进行分层处理,从不同高度对GPT2w模型进行精度评价。由于水汽分布主要集中于对流层的中下层,具有不均匀特性,并且平流层和对流层无明显的分层特性,因此采取垂直不均匀分层方法,按高度分为10层(表 2,单位km),高度表示距离地面的高程。
|
|
表 2 分层高度信息 Tab. 2 The height information of layers |
1) e计算方法。探空站上方的水汽压e可通过探空站提供的露点温度间接计算获得:
| $ e = 6.1078 \times {{\rm{e}}^{\frac{{a \times {T_d}}}{{b + {T_d}}}}} $ | (5) |
式中,Td为露点温度(单位℃),a为系数常数。温度高于0 ℃时,a=17.26,b=237.29;温度低于-40 ℃时,a=21.87,b=265.49;当温度在两者之间时,a和b可采用线性内插获得。
2) Tm计算方法。Tm无法从探空资料中直接获取,部分学者在分析Tm与T、e、P等气象参数关系的基础上已建立不同的Tm经验模型。在众多计算方法中,数值积分法以其容易实现、综合误差影响较小和精度高等优点被广泛使用,本文将以数值积分法获取的Tm作为真值:
| $ {T_m} = \frac{{\int {(e/T)} {\rm{d}}z}}{{\int {\left( {e/{T^2}} \right)} {\rm{d}}z}} $ | (6) |
式中,T为绝对温度(单位K),z为分层高度(单位km)。
3) GNSS-PWV计算方法。首先利用PPP技术,根据GNSS基准站的数据解算得到ZTD[7],再基于站点位置、气压和高程等信息采用Saastamoinen模型计算得到高精度ZHD,两者相减即可得到ZWD(ZWD=ZTD-ZHD),而ZWD乘以水汽转换系数K可得到GNSS-PWV。ZHD计算方法为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{ZHD}} = 0.0022768 \times \frac{{{P_c}}}{{f\left( {{\varphi _c}, {H_c}} \right)}}}\\ {f\left( {{\varphi _c}, {H_c}} \right) = 1 - 0.00266\cos 2{\varphi _c} - 0.00028{H_c}} \end{array}} \right. $ | (7) |
式中,Pc、φc和Hc分别为测站气压、纬度和海拔。
GNSS-PWV与ZWD的关系为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{PWV}} = K \times {\rm{ZWD}}}\\ {K = \frac{{{{10}^5}}}{{{R_v}\left( {{k_3}/{T_m} + k{'_2}} \right)}}} \end{array}} \right. $ | (8) |
式中,K为水汽转换系数,Rv为水汽的比气体常数,Rv=461 J/(kg ·K),其他参数同式(4)。
4) 探空站PWV计算方法。探空站PWV可采用垂直积分法计算获取:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{PWV}} = \frac{1}{{{g_m}}}\int_{{P_z}}^{{P_0}} q {\rm{d}}p}\\ {q = \frac{{622e}}{{p - 0.378e}}} \end{array}} \right. $ | (9) |
式中,q为地面空气比湿(单位g/kg),P0和Pz为地面高度和z高度的气压(单位hPa)。
2.3 统计方法采用偏差(bias)和均方根误差(RMS)对各测站的对流层参数进行精度评定,bias和RMS计算公式为:
| $ {\rm{bias }} = \frac{{\sum\limits_{i = 1}^n {\left( {{x_{{\rm{model }}, i}} - {x_{{\rm{real }}, i}}} \right)} }}{n} $ | (10) |
| $ {\rm{RMS}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{x_{{\rm{model }}, i}} - {x_{{\rm{real }}, i}}} \right)}^2}} }}{n}} $ | (11) |
式中,xmodel, i为GPT2w模型的气象参数值,xreal, i为探空站的气象参数值(视为真值),n为样本数。
3 精度分析 3.1 气象参数精度长三角地区位于中低纬度,春秋两季较短,呈现出以夏冬两季为主的气候特征。本文选取7月代表夏季,1月代表冬季,对GPT2w模型的气象参数进行分析,并分层评价bias和RMS。限于篇幅,仅列出2017年安庆站和阜阳站的分析结果。
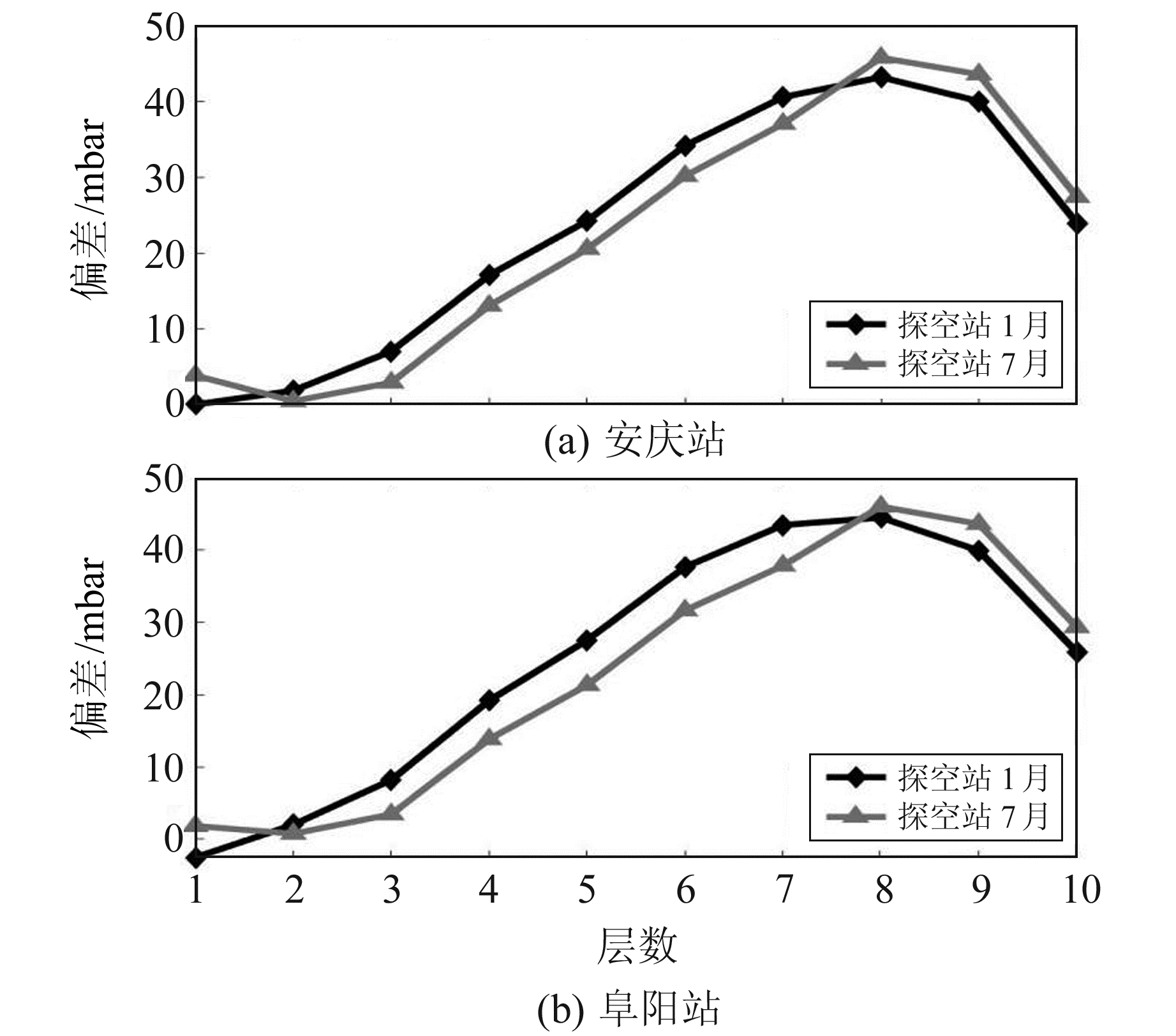
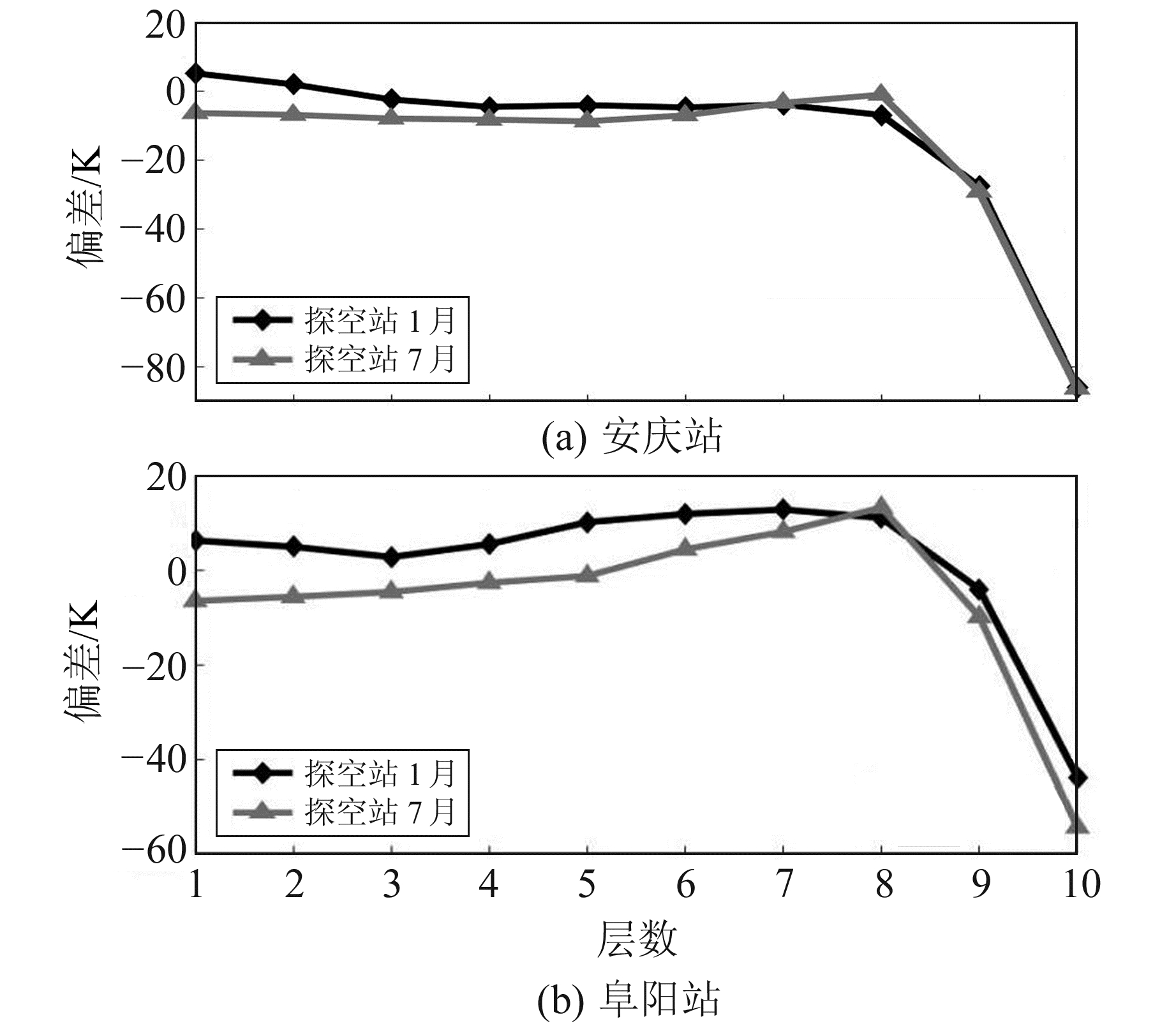
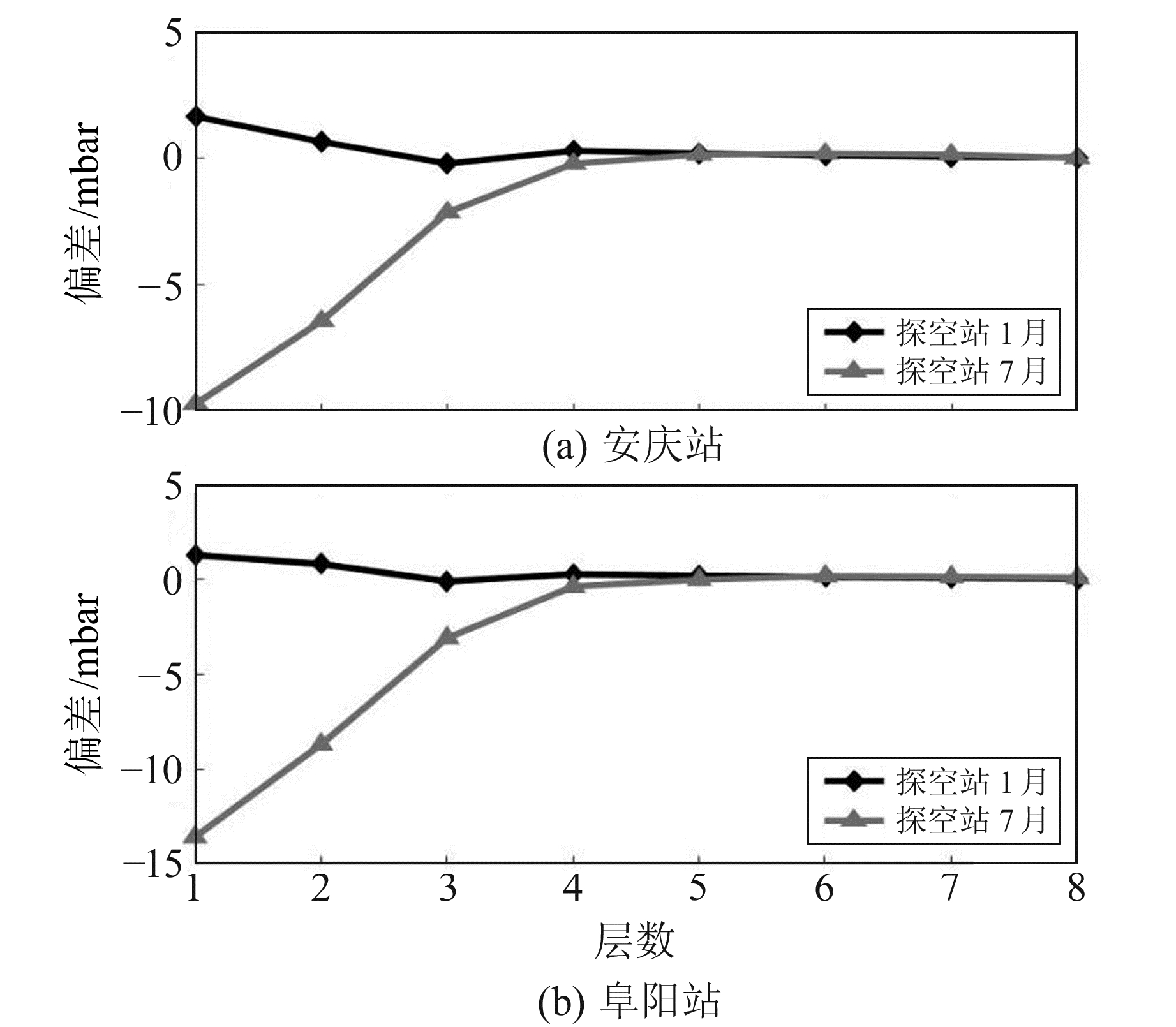
图 2~4分别为安庆站和阜阳站利用GPT2w模型获取的气压、温度、水汽压bias,从图中可以看出,GPT2w模型获取的气压、温度和水汽压在近地面处bias均较小。气压bias随高程增加开始增大,到第8层(14~18 km)时,bias值达到最大,数值为40~50 mbar;温度bias在1~8层波动较为平缓,但到达第8层时迅速增大,且其绝对值远大于近地面处数值。1月的水汽压在各高度处bias波动较小,幅度平缓且精度较高,bias最大为2 mbar;7月的水汽压在地面附近处精度较低,表现为负bias,其中安庆站、阜阳站在第1层(0~1 km)的水汽压bias分别为-10 mbar和-14 mbar,但随着高度增加bias逐渐减小,在第5层后bias逐渐趋于0 mbar。
|
图 2 安庆站和阜阳站气压偏差 Fig. 2 Bias of air pressure at Anqing and Fuyang stations |
|
图 3 安庆站和阜阳站温度偏差 Fig. 3 Bias of air temperature at Anqing and Fuyang stations |
|
图 4 安庆站和阜阳站水汽压偏差 Fig. 4 Bias of water vapor pressure at Anqing and Fuyang stations |
表 3和表 4分别为2017年安庆站和阜阳站的气压、温度和水汽压分层精度统计。从表中可以看出,气压bias和RMS随着层数增加均呈现增大趋势,1月和7月气压的RMS最小值出现在第2层(1~2 km),在2.7~3.5 mbar之间,RMS最大值出现在第8层(14~18 km),在43~46 mbar之间,第8层以上气压的RMS随高度增加逐渐降低;近地面处温度的RMS变化不明显,在5~7 K之间,精度较高,但随着层数增加,RMS值逐渐增大,最大值出现在第10层(>23 km),在45~89 K之间,这是由于GPT2w模型提供的气象参数通过高度归算得到,累积误差会导致精度下滑;水汽压在夏季精度低,冬季精度高,且随着层数增加,RMS一直在0 mbar附近波动,基本保持稳定状态,这是由于实测数据与GPT2w模型的水汽压均由先验指数模型计算得到,因此两者差别较小。
|
|
表 3 2017年安庆站气压、温度和水汽压精度统计 Tab. 3 Accuracy statistics of air pressure, temperature and water vapor pressure at Anqing station in 2017 |
|
|
表 4 2017年阜阳站气压、温度、水汽压精度统计 Tab. 4 Accuracy statistics of air pressure, temperature and water vapor pressure at Fuyang station in 2017 |
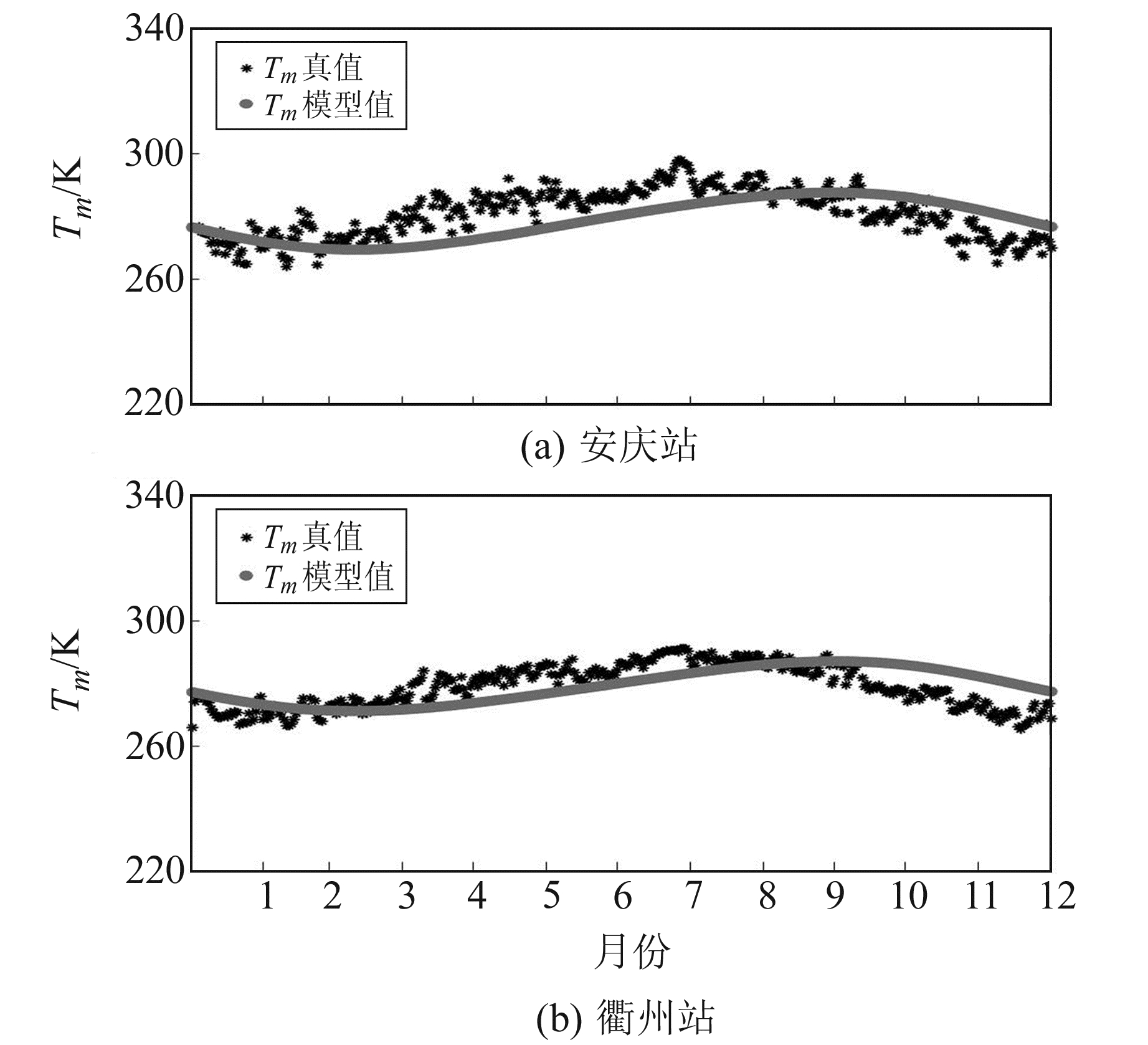
为研究GPT2w模型在长三角地区获取Tm的精度,以数值积分法计算的探空Tm作为真值,与2017年GPT2w模型所得的Tm进行比较。图 5为2017年Tm模型值和真值随时间的变化情况,限于篇幅,仅列出安庆站、衢州站Tm对比图。由图可知,模型值与真值总体变化趋势基本一致。
|
图 5 2017年安庆站与衢州站Tm对比分析 Fig. 5 Comparison of Tm at Anqing and Quzhou stations in 2017 |
表 5(单位K)为2017年长三角地区各探空站Tm全年的bias和RMS,从表中可以看出,GPT2w模型在长三角地区的Tm年均bias和RMS分别为-1.21 K和6.89 K。总体而言,GPT2w模型计算的Tm在长三角地区bias精度较高,RMS精度与文献[6]研究结果接近。
|
|
表 5 2017年7个探空站GPT2w模型Tm精度统计 Tab. 5 Accuracy statistics of Tm derived from GPT2w at 7 radiosonde stations in 2017 |
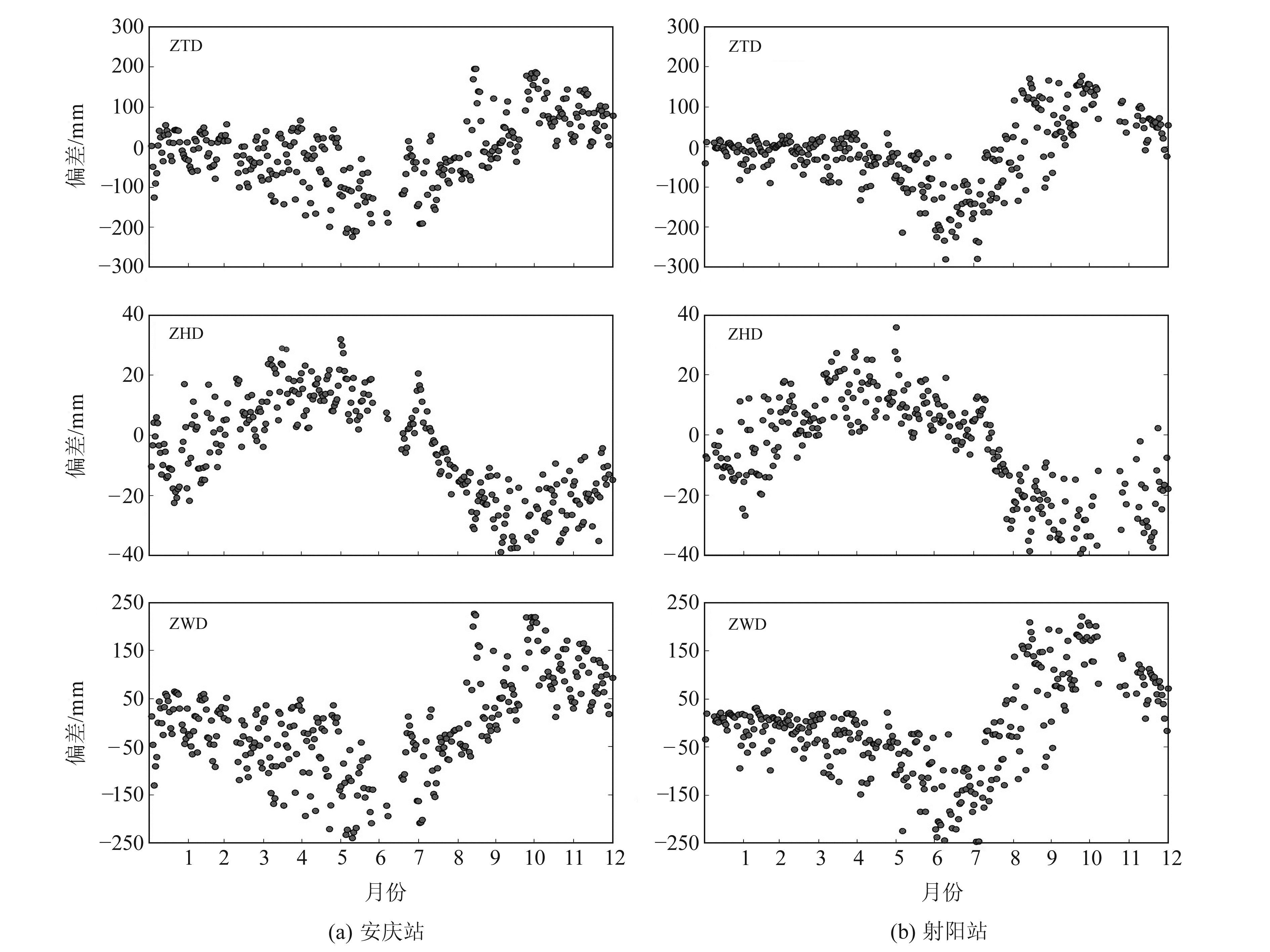
为研究GPT2w模型获取ZTD的精度,本文将2017年安庆站和射阳站2个GNSS站的位置及观测日期等信息代入GPT2w模型,获取相应的ZTD,并与利用GNSS精密单点定位方法[7]解算的GNSS-ZTD进行对比分析。从图 6可以看出,ZHD的bias在0值附近波动,ZTD和ZWD bias的变化趋势基本一致,冬季ZTD精度较高,夏季ZTD精度较低。由于ZHD模型值与真值均采用Saastamoinen模型,且ZHD与地面测站高程、站点纬度和气压具有良好的相关性,因此气压的模型值与实测数据在地面处误差较小。
|
图 6 2017年安庆站和射阳站ZTD、ZHD、ZWD偏差 Fig. 6 Bias of ZTD, ZHD and ZWD at Anqing and Sheyang stations in 2017 |
由表 6(单位cm)可知,安庆站和射阳站ZTD的bias分别为-1.0 cm和-1.7 cm,ZTD的RMS分别为9 cm和9.7 cm,ZTD精度偏低。这是由于GPT2w模型计算ZWD时采用Askne-Nordius模型法[7],该模型中e、Tm等参数与P、T以及高程均具有很强的相关性,多种气象误差累积和交叉影响会造成ZWD精度下滑,因此ZTD精度主要受ZWD精度影响。另外,长三角地区处于中低纬度,主要气候类型为亚热带季风气候,夏季高温多雨,大气中水汽含量比冬季高,因此冬季ZTD精度更高。由式(1)可知,GPT2w模型中基于模型气象元素的时间变化采用包含各参数半年周期和年周期的三角函数式[8],其中α1、β1为各参数的年均值,α2、β2为各参数的半年均值,时间分辨率较低,模型实时性差,仅在半年周期或年周期时间段内具有较高精度,具体的年积日模型数据与实测数据会存在较大差异。
|
|
表 6 2017年安庆站和射阳站ZTD、ZHD、ZWD精度统计 Tab. 6 Accuracy statistics of ZTD, ZHD and ZWD at Anqing and Sheyang stations in 2017 |
以上研究表明,GPT2w模型获取的气象元素具有较高的先验精度,但GPT2w模型在长三角地区的ZTD精度不高,缺乏时效性。本文提出参数互融法,根据式(8)将基于GPT2w模型获取的Tm与基于GNSS获取的ZWD相融合,从而得到更高精度的PWV。
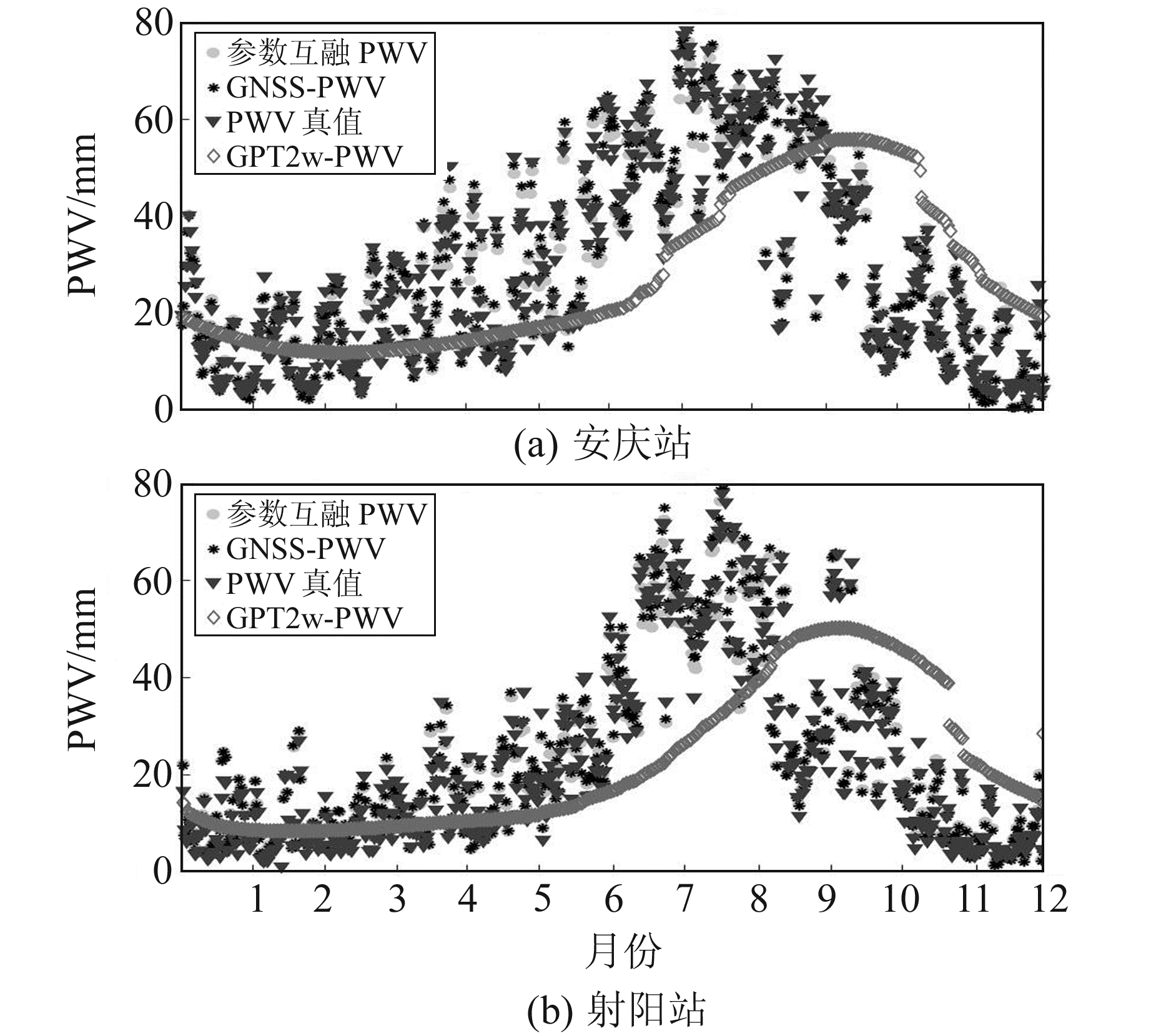
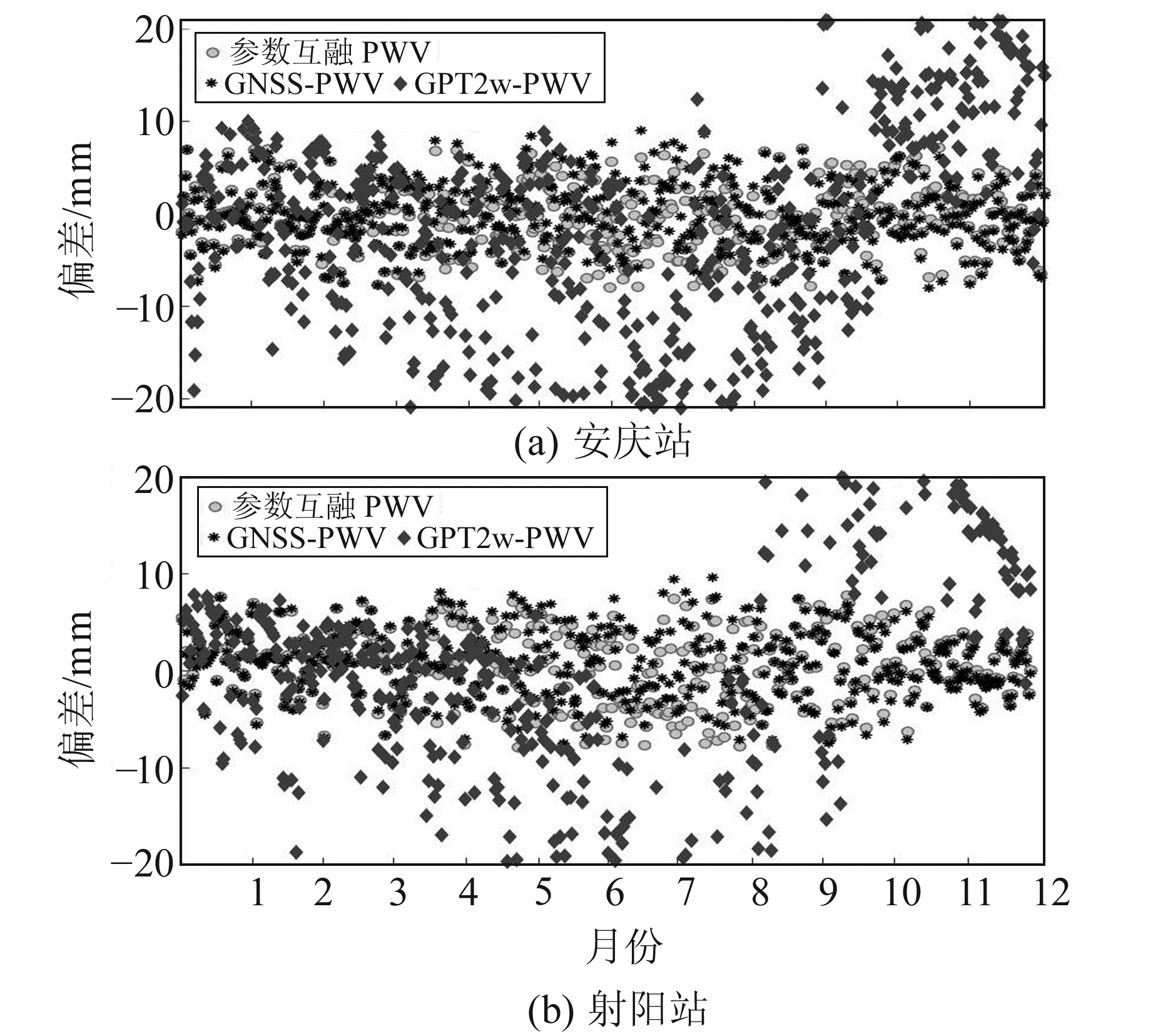
图 7和图 8为安庆站和射阳站基于GPT2w模型的PWV、基于参数融合法的PWV、GNSS-PWV与探空PWV的趋势变化和bias对比结果。由图可知,3种方法计算的PWV变化趋势接近,结合表 7(单位mm)可以看出,GPT2w模型提供的气象参数反演PWV的bias较大,精度较低,而利用参数融合方法和GNSS-ZWD反演PWV的bias大部分集中在5 mm以内。由此可见,基于参数融合法的PWV与GNSS-PWV精度相当,可有效解决GPT2w模型ZTD精度不高的问题。
|
图 7 安庆站和射阳站PWV对比 Fig. 7 Comparison of PWV at Anqing and Sheyang stations |
|
图 8 安庆站和射阳站PWV偏差 Fig. 8 PWV bias at Anqing and Sheyang stations |
|
|
表 7 安庆站和射阳站PWV精度统计 Tab. 7 Accuracy statistics of PWV at Anqing and Sheyang stations |
本文利用2017年长三角地区7个探空站的气象参数,对GPT2w模型的气温、气压、水汽压和Tm进行精度验证,并通过其中2个并址的GNSS基准站,检验GPT2w模型的ZTD精度。针对GPT2w模型误差累积所导致的ZTD和PWV精度不高的问题,提出将GNSS-ZTD与GPT2w模型参数互融,以提高PWV的反演精度。主要结论如下:
1) GPT2w模型的气压、温度在地面附近的bias分布在-3~4 mbar和-7~7 K之间,RMS分别约为4~6 mbar和7 K,随着高度增加,精度有所降低;水汽压的bias和RMS随着高度增加逐渐趋于0 mbar,且表现出明显的季节性特征,冬季精度较高,夏季精度较低。
2) GPT2w模型获取的Tm年均bias为-1.21 K,年均RMS为6.89 K,模型计算的Tm具有可适用性;GPT2w模型获取的ZTD平均bias和RMS分别为1.4 cm和9.4 cm,精度较低。
3) 基于参数融合法获取PWV的bias主要分布在5 mm以内,精度与GNSS-PWV相当。因此,利用GPT2w获得的基本气象要素与Tm具有较高的精度和稳定性,在缺乏实测气象参数时,可将其与GNSS-ZTD相互融合实现当地PWV的快速获取。
| [1] |
Baker H C, Dodson A H, Penna N T, et al. Ground-Based GPS Water Vapour Estimation: Potential for Meteorological Forecasting[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2001, 63(12): 1305-1314 DOI:10.1016/S1364-6826(00)00249-2
(  0) 0) |
| [2] |
Böhm J, Heinkelmann R, Schuh H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683 DOI:10.1007/s00190-007-0135-3
(  0) 0) |
| [3] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069-1073 DOI:10.1002/grl.50288
(  0) 0) |
| [4] |
Möller G, Weber R, Böhm J. Improved Troposphere Blind Models Based on Numerical Weather Data[J]. Navigation, 2014, 61(3): 203-211 DOI:10.1002/navi.66
(  0) 0) |
| [5] |
翟树峰, 吕志平, 李林阳, 等. 基于GPT2w模型化加权平均温度反演可降水量[J]. 大地测量与地球动力学, 2019, 39(7): 733-737 (Zhai Shufeng, Lü Zhiping, Li Linyang, et al. Precipitable Water Vapor Retrieval Based on Weighted Mean Temperature from GPT2w[J]. Journal of Geodesy and Geodynamics, 2019, 39(7): 733-737)
(  0) 0) |
| [6] |
黄良珂, 李琛, 王浩宇, 等. 基于GPT2w模型计算中国地区对流层加权平均温度的精度分析[J]. 大地测量与地球动力学, 2019, 39(5): 496-501 (Huang Liangke, Li Chen, Wang Haoyu, et al. Precision Analysis of the Tropospheric Weighted Mean Temperature Derived from GPT2w Model over China[J]. Journal of Geodesy and Geodynamics, 2019, 39(5): 496-501)
(  0) 0) |
| [7] |
李黎, 匡翠林, 朱建军, 等. 基于实时精密单点定位技术的暴雨短临预报[J]. 地球物理学报, 2012, 55(4): 1129-1136 (Li Li, Kuang Cuilin, Zhu Jianjun, et al. Rainstorm Nowcasting Based on GPS Real-Time Precise Point Positioning Technology[J]. Chinese Journal of Geophysics, 2012, 55(4): 1129-1136 DOI:10.6038/j.issn.0001-5733.2012.04.008)
(  0) 0) |
| [8] |
孟昊霆, 张克非, 杨震, 等. GPT2/GPT2w+Saastamoinen模型ZTD估计的亚洲地区精度分析[J]. 测绘科学, 2020, 45(8): 70-76 (Meng Haoting, Zhang Kefei, Yang Zhen, et al. The Determination of GNSS Zenith Tropospheric Delay by GPT2/GPT2w+Saastamoinen Model and Its Performance Analysis in Asia[J]. Science of Surveying and Mapping, 2020, 45(8): 70-76)
(  0) 0) |
2. Research Center of Beidou Navigation and Environmental Remote Sensing, Suzhou University of Science and Technology, 99 Xuefu Road, Suzhou 215009, China;
3. Jiangsu Institute of Meteorological Sciences, 16 Kunlun Road, Nanjing 210009, China
 2021, Vol. 41
2021, Vol. 41


