区域CORS站时间序列中不仅包含可表征测站多年运动趋势的线性项,也包含测站非线性项以及尚未模型化的残差项。测站线性变化主要由板块构造应力所引起,非线性变化则受地球物理因素影响较多,如热膨胀效应、水文负载、大气负载和无潮汐海洋负载等[1]。对于线性变化,可采用相关模型对参数进行拟合估计,然后对线性项进行建模分析。但对非线性变化而言,由于误差改正模型不完善和区域地理位置差异,非线性项难以完全模型化,这会对区域测站噪声分析、速度估计和负载模型建立等方面造成不利影响。因此,研究如何削弱测站非线性变化,不仅能够优化区域速度场模型,减小残差对区域CORS站噪声特性分析的影响,也对研究区域质量变迁、地壳形变和动态参考框架的建立等方面具有重要意义[2]。
针对如何有效地削弱时间序列中非线性项的问题,部分学者从谐波函数模型出发,利用最小二乘拟合模型中的各项参数,并结合引起测站非线性变化的地球物理因素对非线性项进行修正。王敏等[1]将计算得到的海潮、大气、积雪和土壤水、海洋非潮汐4种环境负载改正用于中国地壳运动观测网络测站中,结果表明负载模型改正效果优于谐波拟合改正效果,但涉及区域较大,并未评估省市级区域的改正效果;姜卫平等[3]研究中国区域及武汉区域环境负载的改正效果发现,环境负载可以削弱约70%测站E方向和U方向的非线性变化,但用于计算环境负载改正的软件较长时间未更新,对现今数据的适用性较差;龚国栋等[4]分析417个全球IGS站环境负载与地理位置的联系发现,环境负载改正具有较强的区域特征,因此研究区域测站非线性改正对精化区域参考框架和建立区域环境负载模型等具有重要意义[5]。
近年来,部分学者从周期项提取的角度提出削弱非线性项的方法。张双成等[6-7]利用经验模态分解(empirical mode decomposition,EMD)方法对测站坐标时间序列进行降噪分析和周期项提取,证实EMD方法可有效分解出噪声项并能够自适应地提取周期项;张恒璟等[8-9]基于EMD方法进行算法改良,提出整体经验模态分解(ensemble empirical mode decomposition,EEMD) 算法,该算法可削弱重构周期项时出现的模态混叠现象,更优地分离出噪声部分和周期部分,但EEMD算法会引入一定量的白噪声且无法完全消除模态混叠现象[10]。以上学者仅对测站坐标时间序列的非线性项进行分解,通过各种指标评定分解效果,但均未对分解重构后的周期项或噪声项作进一步分析。EMD分解可自适应地从复杂信号中提取周期项,环境负载又可对周期项进行改正,基于此本文提出EMD分解与环境负载相结合的方法削弱测站的非线性变化,利用徐州区域10个CORS站近2 a(2016-06~2018-05)的时间序列对此方法进行验证,并与谐波拟合加负载改正方法进行对比分析。
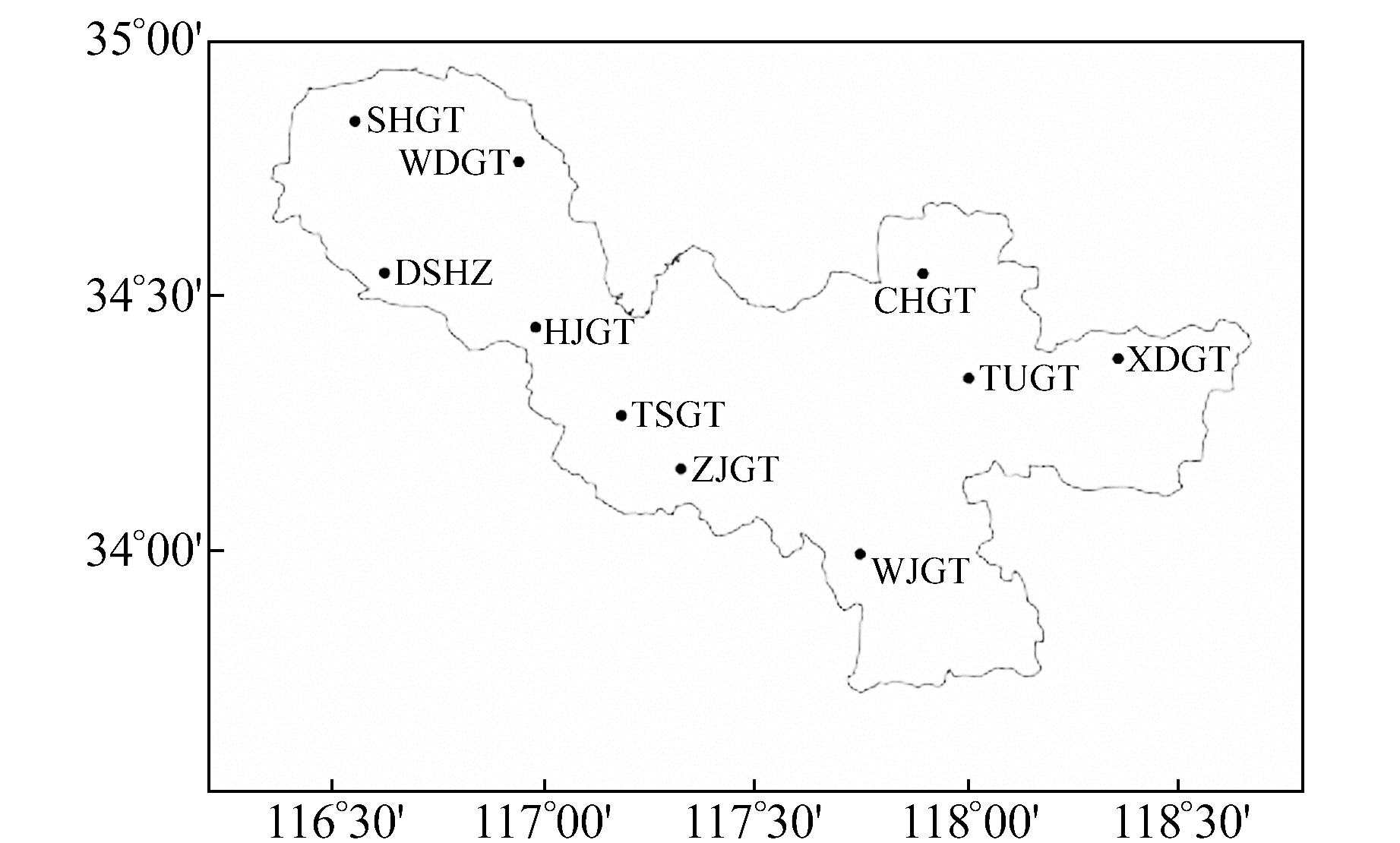
1 实验数据 1.1 XZCORS站数据本次实验数据选用徐州区域近2 a(2016-06~2018-05)10个CORS站的观测数据,分别为CHGT(岔河站)、HJGT(黄集站)、DSHZ(大沙河站)、SHGT(顺河站)、TSGT(铜山站)、TUGT(土山站)、WDGT(五段站)、WJGT(王集站)、XDGT(新店站)和ZJGT(张集站),各测站接收机型号均为LEICA GR10,天线型号均为LEIAR25.R4 LEIT,测站具体分布如图 1所示。
|
图 1 徐州市CORS站分布 Fig. 1 Distribution of CORS stations in Xuzhou city |
本次实验采用水文负载(HYDL,hydrological loading)、非潮汐大气负载(NTAL,non-tidal atmospheric loading)和无潮汐海洋负载(NTOL,non-tidal oceanic loading)3种负载改正产品。水文负载改正选用德国地学研究中心(GFZ)根据全球水文模型LSDM[11]得出的结果,已考虑积雪深度、土壤湿度和地表水,空间分辨率为0.5°×0.5°,时间分辨率为24 h;非潮汐大气负载(也称为大气负载)改正采用GFZ根据ECMWF模型得出的结果,空间分辨率为0.5°×0.5°,时间分辨率为3 h;无潮汐海洋负载改正选用GFZ根据MPIOM[12]模型得出的结果,空间分辨率为1.0°×1.0°,时间分辨率为3 h。
2 实验方案 2.1 数据处理本文利用Bernese软件(Linux 5.2)自动处理功能(BPE, Bernese processing engine)调用非差模块,对徐州市10个CORS站的坐标时间序列进行解算。具体解算策略为[13]:采用非差模式解算;截止高度角为10°,历元间隔为30 s;电离层折射采用LC观测值进行消除;对流层延迟采用Saastamoinen模型进行改正;对固体潮、海潮、极潮和大气潮进行改正;重力场模型采用EGM2008;加入震后形变模型。对解算后的数据进行粗差剔除和插值,由于较多测站数据缺失严重,本文仅选用数据较为连续的HJGT(黄集站)和SHGT(顺和站)为例进行说明。
2.2 评价指标本文利用EMD方法将去线性项的时间序列分解成从高频到低频的本征模态函数分量(intrinsic mode function,IMF),并将相关系数首次出现的局部极小值点作为分界点,分离出噪声项与非线性项。其中相关系数表达式为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;R(y, {\rm{IMF}}) = \\ \frac{{\mathop \sum \limits_m^U \left[ {y\left( t \right) - \bar y} \right]\left[ {{\rm{IM}}{{\rm{F}}_m}\left( t \right) - \overline {{\rm{IMF}}} } \right]}}{{\sqrt {\mathop \sum \limits_m^U {{\left[ {y\left( t \right) - \bar y} \right]}^2}} \sqrt {\mathop \sum \limits_m^U {{\left[ {{\rm{IM}}{{\rm{F}}_m}\left( t \right) - \overline {{\rm{IMF}}} } \right]}^2}} }} \end{array} $ | (1) |
式中,t代表时间,m代表采样个数,U代表采样总数,y(t)表示去线性项后的时间序列,IMFm(t)表示第m个IMF分量数值。其中,
均方根(root mean square, RMS)减少量可以衡量EMD与环境负载改正方法以及谐波拟合加环境负载改正方法对时间序列中非线性项的改正效果,在求取RMS值减少量之前,需要对时间序列进行去线性项处理。RMS表达式为:
| $ {\mathop{\rm RMS}\nolimits} = \sqrt {\frac{{\sum\limits_1^n {\left( {{G_i} - \frac{{\sum\limits_1^n {{G_i}} }}{n}} \right)} }}{{n - 1}}} $ | (2) |
式中,n代表观测值个数,即连续时间跨度;Gi表示EMD或环境负载改正的位移量,i代表天数。
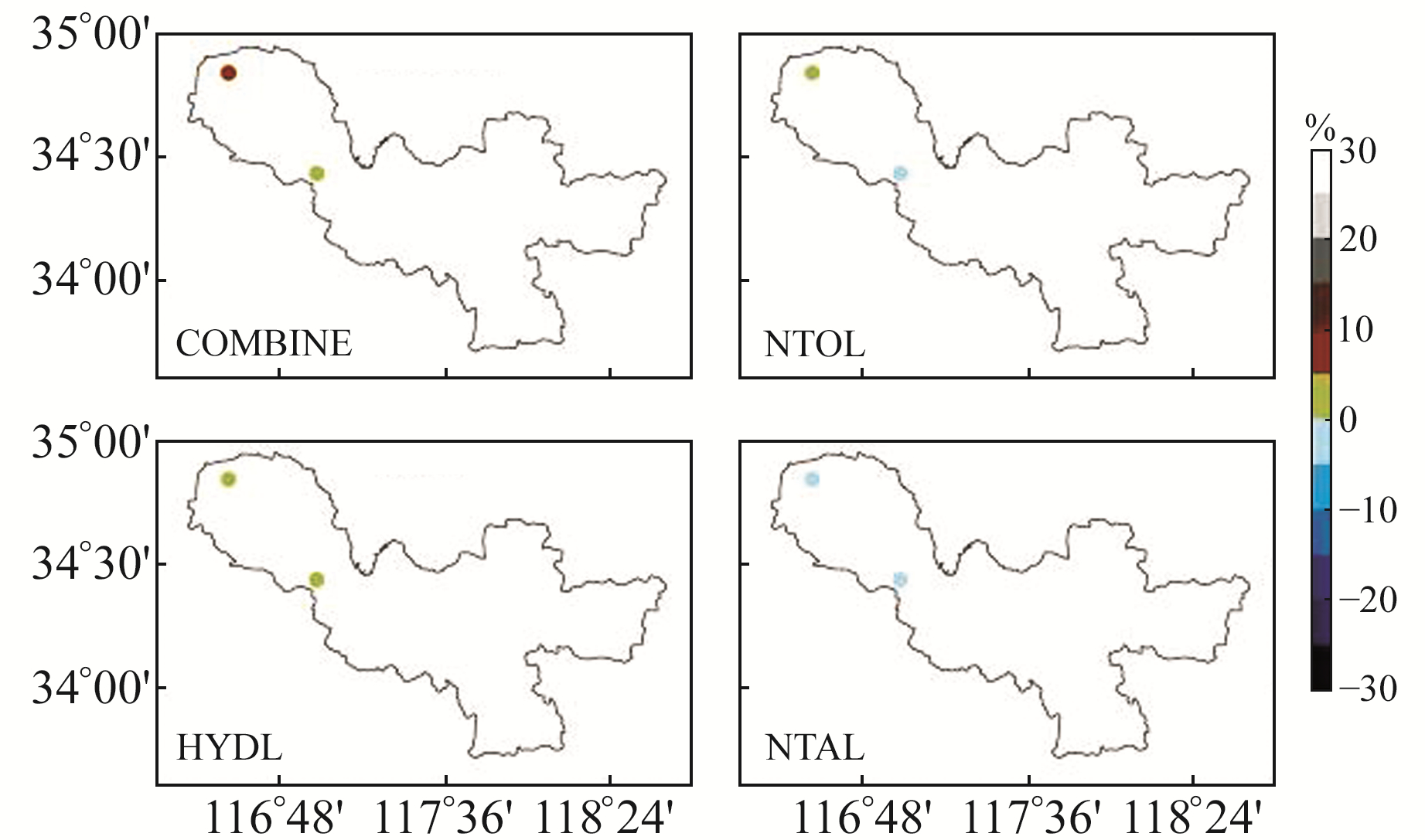
3 结果分析以SHGT和HJGT测站为例,采用函数拟合加环境负载改正和EMD加环境负载改正两种方法对非线性项进行修正,具体结果如图 2~7所示。图 2~4中COMBINE表示当水文负载、大气负载和无潮汐海洋负载产品改正有效时多种负载产品的组合;图 5~7中COMBINE表示当负载改正对提取的周期项具有修正效果时负载产品的组合。
|
图 2 LS拟合和环境负载改正下N方向RMS变化率 Fig. 2 The RMS variation rate in the N direction after LS fitting and environmental loading correction |
|
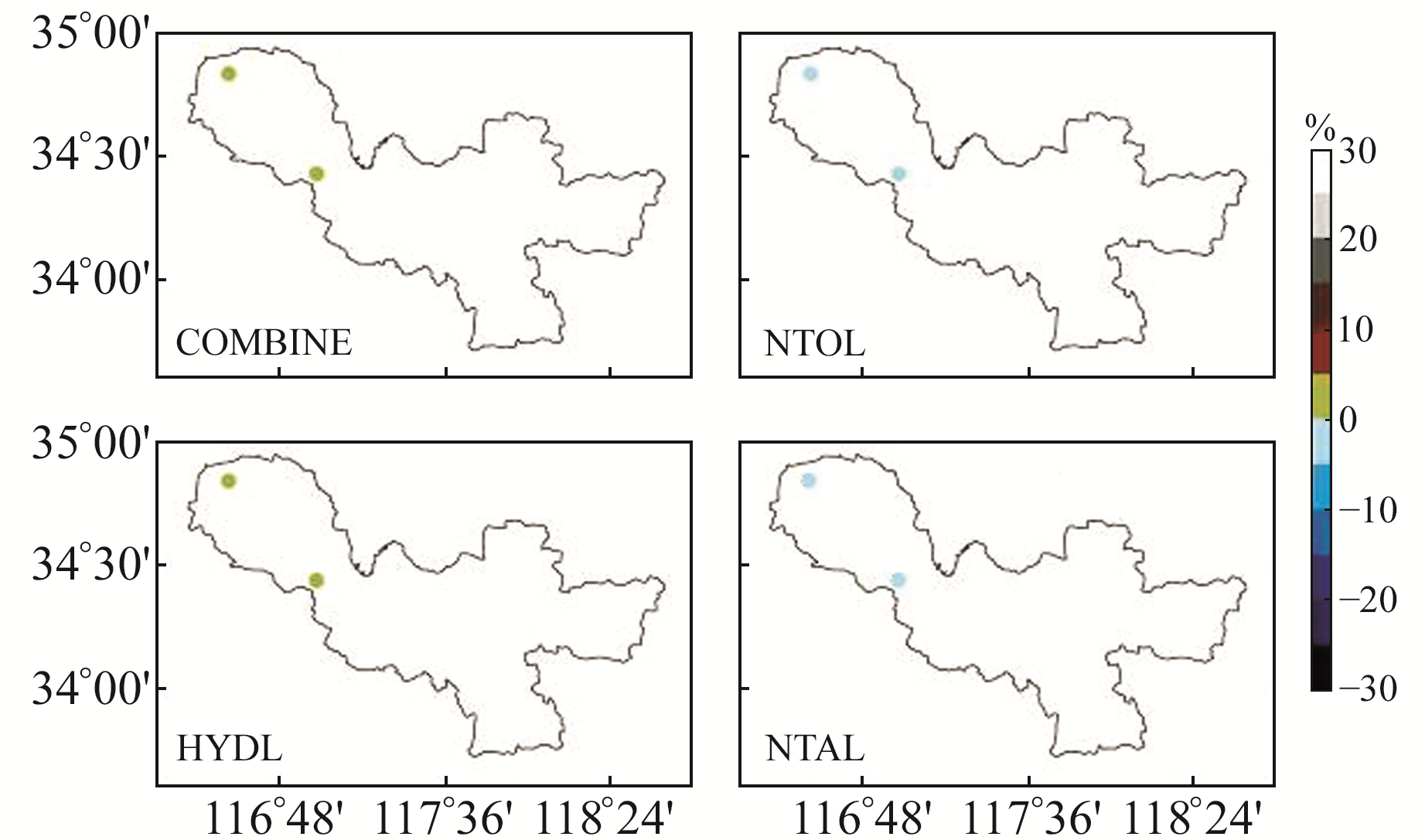
图 3 LS拟合和环境负载改正下E方向RMS变化率 Fig. 3 The RMS variation rate in the E direction after LS fitting and environmental loading correction |
|
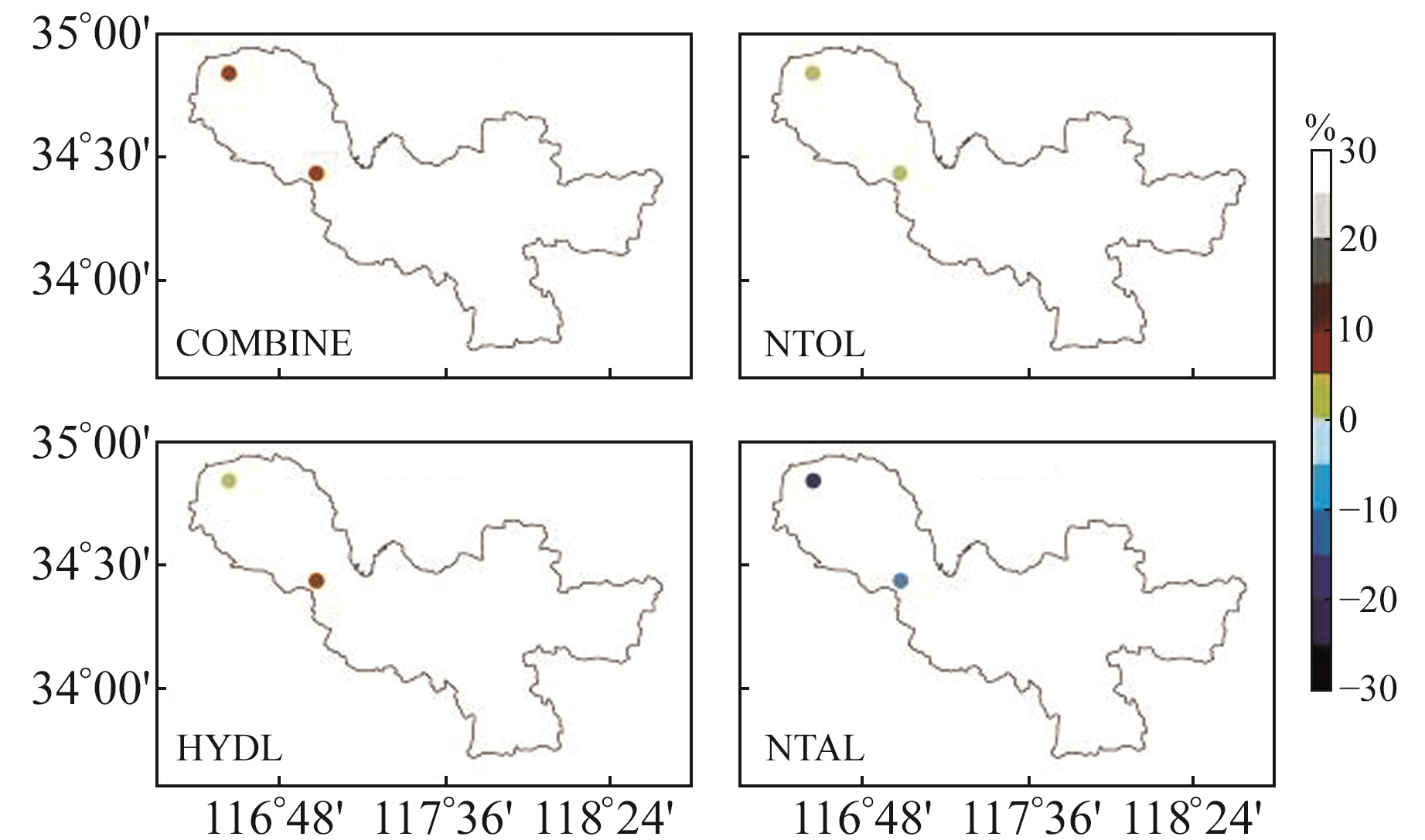
图 4 LS拟合和环境负载改正下U方向RMS变化率 Fig. 4 The RMS variation rate in the U direction after LS fitting and environmental loading correction |

|
图 5 EMD和环境负载改正下N方向RMS变化率 Fig. 5 The RMS variation rate in the N direction after EMD and environmental loading correction |
|
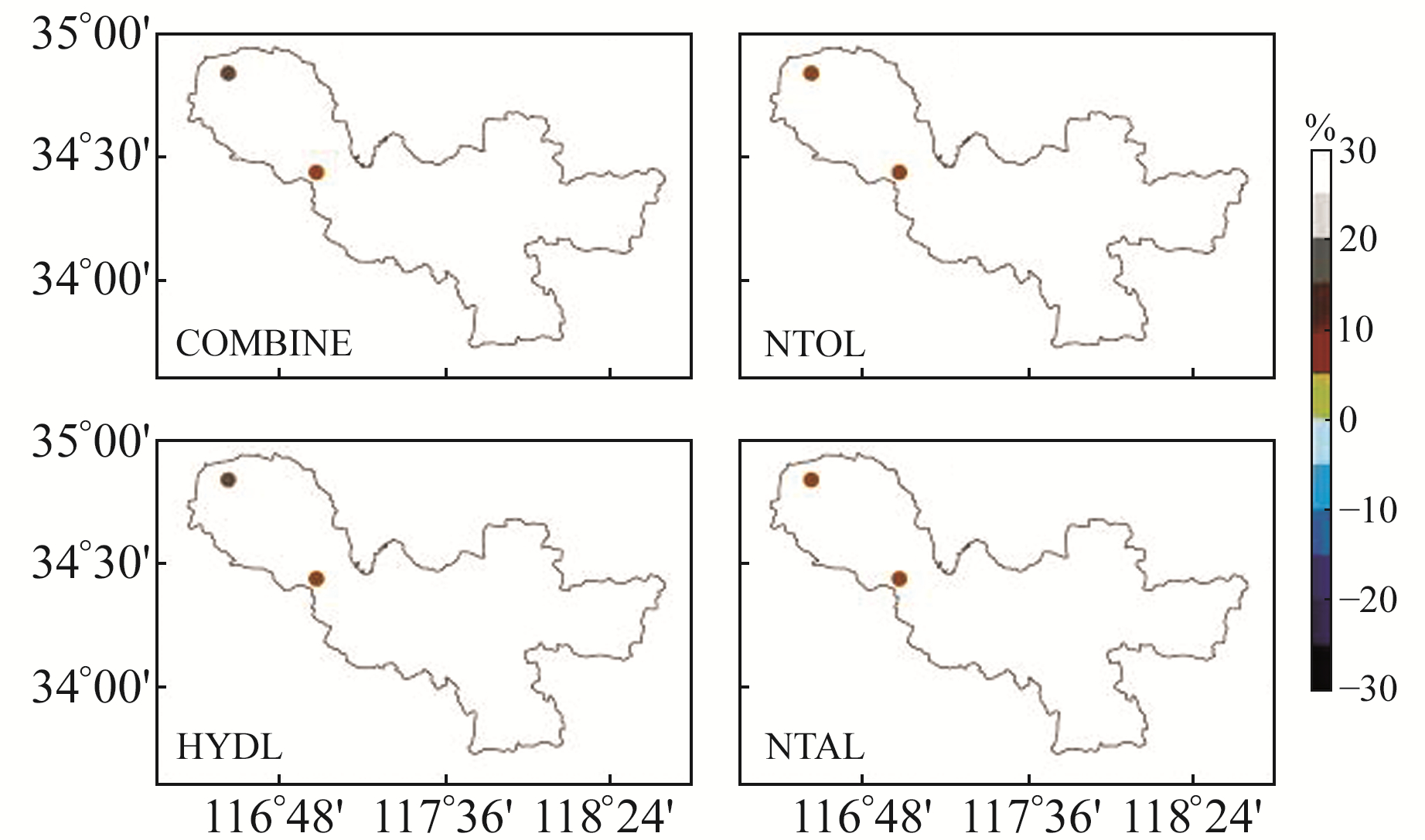
图 6 EMD和环境负载改正下E方向RMS变化率 Fig. 6 The RMS variation rate in the E direction after EMD and environmental loading correction |
|
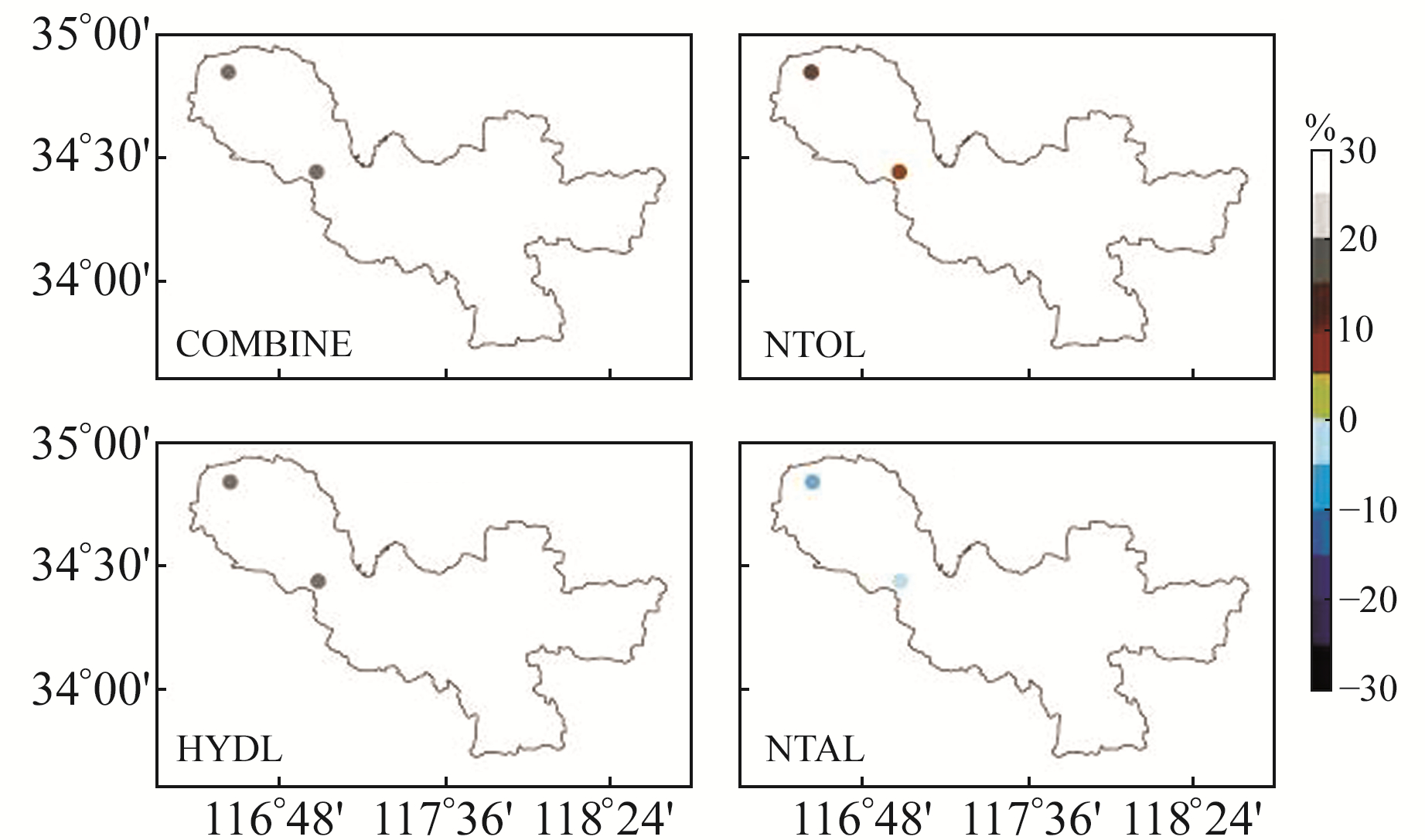
图 7 EMD和环境负载改正下U方向RMS变化率 Fig. 7 The RMS variation rate in the U direction after EMD and environmental loading correction |
图 2~4为经过谐波函数拟合与环境负载改正后各方向RMS值的变化率,由图可知,水文负载和无潮汐海洋负载产品对徐州区域CORS站的坐标时间序列具有修正效果,大气负载产品无改正效果;水文负载和无潮汐海洋负载产品在N方向和E方向改正效果较差,最大仅为2.1%,但对U方向改正效果较好,最大可达7.3%;负载产品的综合改正效果均优于单个负载产品。
图 5~7为对去线性项的时间序列进行EMD分解,并对重构周期项进行环境负载改正。由图可知,3种负载产品对徐州区域CORS站坐标时间序列的非线性项均具有较好的修正效果,最高可达16.9%;U方向水文负载改正和无潮汐海洋负载改正的效果普遍比N方向和E方向的改正效果好,而且U方向水文负载改正效果优于无潮汐海洋负载改正;不同负载产品的组合改正效果普遍优于单个负载产品,最大改正率可达19.4%。
综合对比各图可知,函数拟合加负载改正可以在一定程度上削弱非线性项,但与EMD分解加负载改正相比,后者改正效果较为明显,因此本文所提方法的改正效果更优。从两种方法对非线性项的改正效果可以看出,U方向的改正效果远优于N方向和E方向,负载改正对U方向影响较大;不同负载产品的组合改正效果均优于单一负载产品,但不同区域要选用适当的负载组合对分解的周期项进行改正。
4 结语针对徐州区域CORS站坐标时间序列,利用函数拟合加负载改正和EMD加负载改正两种方法对非线性项进行改正,对比分析RMS值的改变量,得出以下结论:
1) EMD加负载产品改正对徐州区域CORS站坐标时间序列非线性项的改正效果优于函数拟合加负载改正,因此本文所提方法具有一定的有效性和实用性。
2) 在利用两种方法对非线性项进行改正时,各测站在N方向和E方向改正效果不明显,U方向改正效果明显,负载产品的综合改正效果优于单个产品改正效果。
3) 受水文、气象、海拔高度和板块等地理因素影响,不同区域CORS站坐标时间序列的非线性项改正应选用不同的环境负载产品。对于负载产品的综合选取,应根据改正效果选用不同产品进行综合改正,徐州区域CORS站坐标时间序列的非线性项改正应综合选用水文负载产品与无潮汐海洋负载产品。
| [1] |
王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1045-1052 (Wang Min, Shen Zhengkang, Dong Danan. Effects of Non-Tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1045-1052 DOI:10.3321/j.issn:0001-5733.2005.05.010)
(  0) 0) |
| [2] |
He X X, Montillet J P, Fernandes R, et al. Review of Current GPS Methodologies for Producing Accurate Time Series and Their Error Sources[J]. Journal of Geodynamics, 2017, 106: 12-29 DOI:10.1016/j.jog.2017.01.004
(  0) 0) |
| [3] |
姜卫平, 夏传义, 李昭, 等. 环境负载对区域GPS基准站时间序列的影响分析[J]. 测绘学报, 2014, 43(12): 1217-1223 (Jiang Weiping, Xia Chuanyi, Li Zhao, et al. Analysis of Environmental Loading Effects on Regional GPS Coordinate Time Series[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1217-1223)
(  0) 0) |
| [4] |
龚国栋, 花向红, 贺小星, 等. GPS坐标时间序列中地表环境负载效应区域特征分析[J]. 大地测量与地球动力学, 2017, 37(9): 961-967 (Gong Guodong, Hua Xianghong, He Xiaoxing, et al. Analysis of Regional Characteristics of Environment Load Effect in GPS Coordinate Time Series[J]. Journal of Geodesy and Geodynamics, 2017, 37(9): 961-967)
(  0) 0) |
| [5] |
姜卫平, 李昭, 刘万科, 等. 顾及非线性变化的地球参考框架建立与维持的思考[J]. 武汉大学学报: 信息科学版, 2010, 35(6): 665-669 (Jiang Weiping, Li Zhao, Liu Wanke, et al. Some Thoughts on Establishment and Maintenance of Terrestrial Reference Frame Considering Non-Linear Variation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 665-669)
(  0) 0) |
| [6] |
张双成, 何月帆, 李振宇, 等. EMD用于GPS时间序列降噪分析[J]. 大地测量与地球动力学, 2017, 37(12): 1248-1252 (Zhang Shuangcheng, He Yuefan, Li Zhenyu, et al. EMD for Noise Reduction of GPS Time Series[J]. Journal of Geodesy and Geodynamics, 2017, 37(12): 1248-1252)
(  0) 0) |
| [7] |
张双成, 李振宇, 何月帆, 等. GNSS高程时间序列周期项的经验模态分解提取[J]. 测绘科学, 2018, 43(8): 80-84 (Zhang Shuangcheng, Li Zhenyu, He Yuefan, et al. Extracting of Periodic Component of GNSS Vertical Time Series Using EMD[J]. Science of Surveying and Mapping, 2018, 43(8): 80-84)
(  0) 0) |
| [8] |
张恒璟, 程鹏飞. 基于EEMD的GPS高程时间序列噪声识别与提取[J]. 大地测量与地球动力学, 2014, 34(2): 79-83 (Zhang Hengjing, Cheng Pengfei. Noise Recognition and Extraction of GPS Height Time Series Based on EEMD[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 79-83)
(  0) 0) |
| [9] |
张恒璟, 齐昕, 文汉江. 基于K均值聚类EEMD的CORS高程时间序列信号分析方法[J]. 大地测量与地球动力学, 2019, 39(10): 1053-1057 (Zhang Hengjing, Qi Xin, Wen Hanjiang. Analytical Method of CORS Height Time Series Based on K-Means Clustering EEMD[J]. Journal of Geodesy and Geodynamics, 2019, 39(10): 1053-1057)
(  0) 0) |
| [10] |
施闯, 牛玉娇, 魏娜, 等. HHT-EEMD用于IGS站高程时间序列分析[J]. 大地测量与地球动力学, 2018, 38(7): 661-667 (Shi Chuang, Niu Yujiao, Wei Na, et al. Application of the HHT-EEMD Approach in Analysis of GPS Height Time Series[J]. Journal of Geodesy and Geodynamics, 2018, 38(7): 661-667)
(  0) 0) |
| [11] |
Dill R, Dobslaw H. Numerical Simulations of Global-Scale High-Resolution Hydrological Crustal Deformations[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(9): 5008-5017 DOI:10.1002/jgrb.50353
(  0) 0) |
| [12] |
Jungclaus J H, Fischer N, Haak H, et al. Characteristics of the Ocean Simulations in the Max Planck Institute Ocean Model(MPIOM) the Ocean Component of the MPI-Earth System Model[J]. Journal of Advances in Modeling Earth Systems, 2013, 5(2): 422-446 DOI:10.1002/jame.20023
(  0) 0) |
| [13] |
Dach R, Walser P. Bernese GNSS Software Version 5.2[Z]. 2013
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


