2. 空中交通管理系统与技术国家重点实验室,南京市永智路8号,210016
全球导航卫星系统的地基增强系统(ground-based augmentation system, GBAS)可提供差分校正[1],同时可确保飞机精密进近导航解决方案的完好性[2]。GBAS地面站可监视每个测距源,以防止导航出现误差[3],从而确保GBAS用户的导航完好性。GBAS测距源故障可分为两类:一种为影响差分校正误差的叠加性偏差,主要由码/载波分歧(code-carrier divergence, CCD)故障引起[4-5];另一种故障会影响差分校正误差的方差,主要由卫星信号低功率故障引起。为了确保GBAS系统的完好性,对于每类测距源故障,应在GBAS地面站设置监视器[6],监视器可在信号质量监测(signal quality monitoring, SQM)过程中计算用于指示特定故障的阈值,以避免由于测距源故障导致GBAS用户的完好性风险。因此,对上述监测量设定合理的阈值是使监视器能够正常工作的关键。
在实际应用中通常假设CCD监测量和信号功率监测量的载噪比服从高斯分布[7],但由于受多径效应等影响,实际监测量并不服从高斯分布,尤其是在监测值概率密度函数的边缘部分,高斯分布并不能准确地描述监测值,因此只能将高斯分布计算的阈值进行膨胀,但这会导致最终的阈值过于保守,不能很好地反映监测量的实际分布[8]。近年来部分学者发现稳定分布在处理随机信号噪声、股市预测等非高斯分布的数据时具有很好的效果和适用性[9-11];Xue等[12]提出一种基于稳定分布的GBAS保护级计算方法,表明稳定分布在空管导航领域具有广阔的应用前景。
基于上述情况,本文提出一种基于稳定分布的SQM监测量阈值模型,利用稳定分布对载噪比和CCD监测量的精确描述计算其阈值,使阈值能够更加精准地包络监测量参数样本,并通过实测数据对阈值的合理性进行验证。
1 基于高斯分布的SQM阈值模型SQM算法是GBAS系统完好性算法中的重要组成部分,目的是及时发现测距信号中存在的异常情况。接收信号功率监测和码/载波分歧监测作为SQM算法的2个重要功能,其阈值设定是否准确至关重要[13]。
1.1 载噪比阈值模型接收信号功率监测功能主要是判断接收到的GNSS信号功率是否符合国际规范,当信号载噪比过低时,接收机很难将噪声与信号分离,会使测距误差增大,导致发生完好性风险的概率随之增加。传统的载噪比阈值模型建立过程如下。
GBAS地面站对接收机接收到的载噪比进行平均处理,对于每个信道,载噪比平均值为:
| $ \begin{array}{l} {\rm{CN}}{{\rm{R}}_{{\rm{avg}}, (i, j)}} = \frac{1}{2}\left( {{\rm{CN}}{{\rm{R}}_{(i, j)}}(k) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {{\rm{CN}}{{\rm{R}}_{(i, j)}}(k - 1)} \right) \end{array} $ | (1) |
式中,CNRavg, (i, j)为某时刻接收机j接收到卫星i的信号载波和噪声功率的比值,此时接收机j接收到卫星i的信号可构成1个接收机通道,k和k-1分别为当前时刻和前一时刻。
将全部卫星的观测值作为一个整体,计算信号功率的监测统计量载噪比,然后根据仰角区间对载噪比进行分组,每10°为1组,假设对应每颗可见卫星的每组载噪比服从高斯分布:
| $ {\rm{CN}}{{\rm{R}}_{{\rm{avg}}, (i, j)}} \sim N\left( {{\mu _{{\rm{cnr}}, (i, j)}}, {\sigma _{{\rm{cnr}}, (i, j)}}} \right) $ | (2) |
计算每组载噪比数据的均值μ(i, j)和标准差σ(i, j),则监测量阈值为:
| $ {T_{{\rm{cnr}}, (i, j)}} = {\mu _{(i, j)}} - K{\sigma _{(i, j)}} $ | (3) |
考虑到误警率设定以及安全需求,通常将膨胀系数K设定为6,这在很大程度上可避免阈值无法包络载噪比的情况,但会导致由高斯分布计算所得的阈值过于保守,从而影响GBAS系统的可靠性。
在计算得到阈值后,将每时刻的CNRavg, (i, j)和阈值相比,若平均载噪比大于阈值则通过检测,若小于阈值则给对应的接收机通道设置功率小于阈值的标志。
1.2 CCD阈值模型在理想情况下,同一颗卫星在同频率上相邻2个历元的测码伪距和测相伪距之差相等,码/载波分歧监测是通过实时监测测码伪距观测量和载波相位观测量之间的偏差并进行处理,监测由于电离层异常、多径效应等因素引起的信号延迟或偏移[14]。目前实现CCD监测的主要手段是采用几何移动平均的方法来估计码/载波分歧监测量,可表示为:
| $ \begin{array}{l} {\rm{CC}}{{\rm{D}}_{m, n}}(k) = \frac{{{\tau _d} - {T_s}}}{{{\tau _d}}}{\rm{CC}}{{\rm{D}}_{m, n}}(k - 1) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{{\tau _d}}}{\rm{d}}{Z_{m, n}}(k) \end{array} $ | (4) |
| $ {Z_{m, n}}(k) = {\rho _{m, n}}(k) - {\varphi _{m, n}}(k) $ | (5) |
式中,CCD(m, n)(k)为码/载波分歧监测量;τd为平均持续时间,取值200 s;Ts为地基增强系统测量值的更新频率,一般为0.5 s;Z(m, n)(k)为k时刻码减载波观测量;ρm, n(k)为k时刻原始伪距观测量;φm, n(k)为对应k时刻的载波观测量;m和n分别为卫星和接收机编号。
与载噪比阈值的建模过程类似,将全部卫星的观测值作为一个整体计算CCD值,然后根据仰角区间对CCD监测量进行分组,不考虑仰角小于10°的卫星,每10°为一组,假设对应每颗可见卫星的每组CCD服从高斯分布:
| $ {\rm{CC}}{{\rm{D}}_{(i, j)}} \sim N\left( {{\mu _{{\rm{ccd}}, (i, j)}}, {\sigma _{{\rm{ccd}}, (i, j)}}} \right) $ | (6) |
与载噪比数据的建模过程类似,CCD检测量阈值为:
| $ {T_{{\mathop{\rm ccd}\nolimits} , (i, j)}} = {\mu _{(i, j)}} \pm 6{\sigma _{(i, j)}} $ | (7) |
将CCD监测值与阈值进行比较可确定电离层是否出现异常,因此合适的阈值模型对GBAS至关重要。
2 基于稳定分布的SQM阈值模型 2.1 稳定分布与最大似然估计稳定分布作为一种可替代高斯分布处理部分非高斯性数据的方法,其不同于常见类型的分布函数,通常可表示为:
| $ \mathit{\Phi } (t) = \exp \left( {{\rm{j}}\delta t - |\gamma t{|^a}\left( {1 - {\rm{j}}\beta {\mathop{\rm sgn}} (t)\tan \left( {\frac{{\pi \alpha }}{2}} \right)} \right)} \right) $ | (8) |
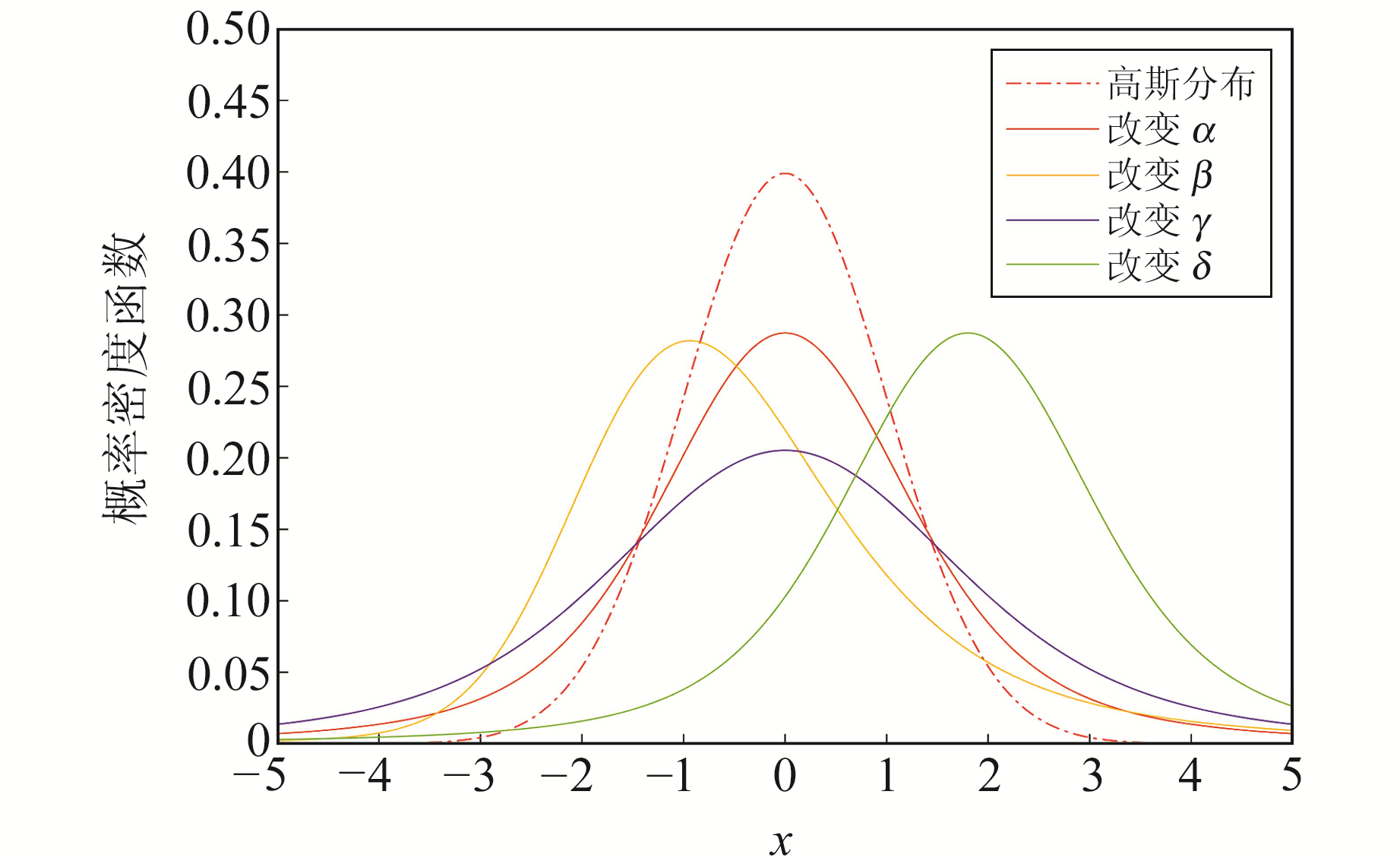
式中,j为复数单位;sgn为符号函数;α为稳定分布的特征参数,可决定概率密度函数尾部的厚度;β为对称系数,可决定稳定分布相对于中心的偏斜程度,当β=0时,稳定分布具有对称性;γ为分散系数,可描述稳定分布相对于中心的扩散程度,类似于高斯分布中的方差概念;δ为位置参数,与β共同决定函数分布形状。通过改变稳定分布参数可以描述部分具有非高斯特性(如不对称性)的数据(图 1)。
|
图 1 稳定分布参数对概率密度函数的影响 Fig. 1 The influence of stable distribution parameters on probability density function |
在对SQM监测量参数进行建模过程中,由于稳定分布的特性完全由特征函数中α、β、γ、δ参数决定,因此利用服从稳定分布的样本来实现4个参数的准确估计至关重要,在本文中选用相对精度最高的最大似然估计对载噪比样本和CCD监测量样本进行稳定分布参数估计。
最大似然估计(maximum likelihood estimation, MLE)为贝叶斯推理的简化,在不考虑先验信息的情况下,通过最大化对数似然函数对稳定分布进行参数估计。对于给定的独立同分布的观测矢量x=x1, x2, …, xn,α稳定分布中参数θ=(α, β, γ, δ)的最大似然估计就是使式(9)最大化:
| $ L(\theta ) = \sum\limits_{i = 1}^n {\log } f\left( {{x_i};\theta } \right) $ | (9) |
式中,f(xi; θ)为α稳定分布的概率密度函数。最大似然估计的重要特性是其为一致渐进正态估计器,即若
通过快速傅里叶变换对稳定分布特征函数进行反变换得到稳定分布对数似然函数,分别对α、γ、δ求偏导,求解式(10)即可得到稳定分布参数:
| $ \frac{{\partial L(P)}}{{\partial \alpha }} = \frac{{\partial L(P)}}{{\partial \gamma }} = \frac{{\partial L(P)}}{{\partial \delta }} = 0 $ | (10) |
稳定分布模型的显著特点是比常规高斯信号或噪声具有更显著的尖峰脉冲,因此其概率密度函数图像上具有显著的拖尾现象,适用于描述部分具有非高斯性质的样本。
以载噪比阈值的建模过程为例,给出基于稳定分布的载噪比误差模型,将载噪比数据进行分组,每组仰角区间的载噪比服从稳定分布,即
| $ {\rm{CN}}{{\rm{R}}_{(i, j)}} \sim S\left( {{\alpha _{(i, j)}}, {\beta _{(i, j)}}, {\gamma _{(i, j)}}, {\delta _{(i, j)}}} \right) $ | (11) |
对于每个信道,使用最大似然估计对在仰角区间内采集到的载噪比监测量进行参数估计,使用式(10)得到每个仰角区间的4个稳定分布参数,则载噪比监测量在该仰角区间的阈值为:
| $ {T_{{\rm{cnr}}, \max }} = {Q_s}\left( {{P_{{\rm{cnr}}}};{\alpha _{{\rm{cnr}}}};{\beta _{{\rm{cnr}}}};{\sigma _{{\rm{cnr}}}};{\delta _{{\rm{cnr}}}}} \right) $ | (12) |
式中,Pcnr为置信参数,可通过所需的误警率选择合适的置信参数;Qs为在某组稳定分布参数下,对应某个置信参数的分位点。
使用稳定分布对CCD监测量进行建模,则CCD监测量在某仰角区间的阈值为:
| $ {T_{{\mathop{\rm ccd}\nolimits} , \max }} = {Q_s}\left( {P;{\alpha _{{\rm{ccd}}}};{\beta _{{\rm{ccd}}}};{\sigma _{{\rm{ccd}}}};{\delta _{{\rm{ccd}}}}} \right) $ | (13) |
| $ {T_{{\rm{ccd}}, \min }} = Qs\left( {1 - P;{\alpha _{{\rm{ccd}}}};{\beta _{{\rm{ced}}}};{\sigma _{{\rm{ccd}}}};{\delta _{{\rm{ccd}}}}} \right) $ | (14) |
式中,Tccd, max和Tccd, min分别为上阈值和下阈值,在稳定分布阈值建模过程中,上下阈值由置信参数决定,上下阈值对应的置信参数之和为1。
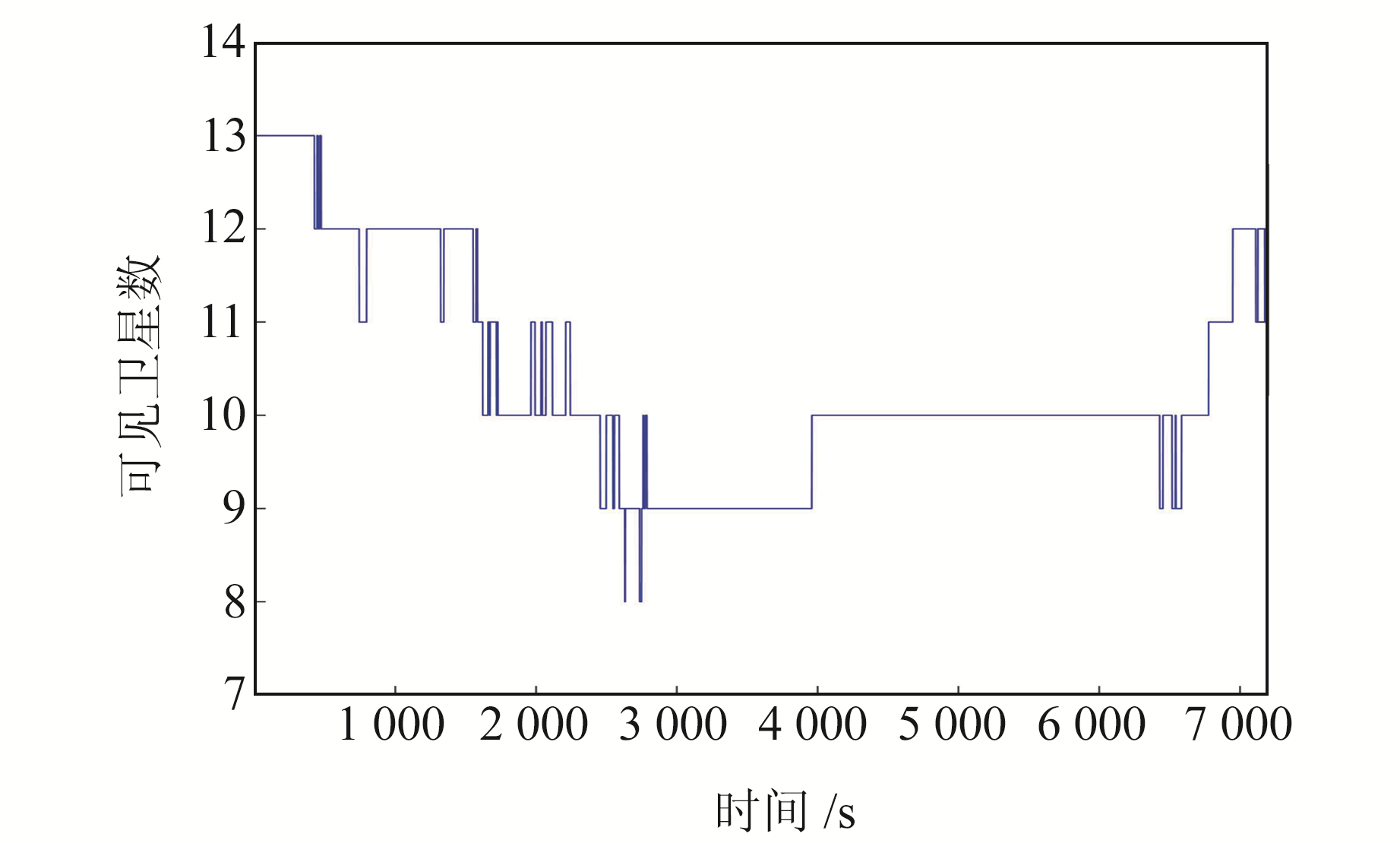
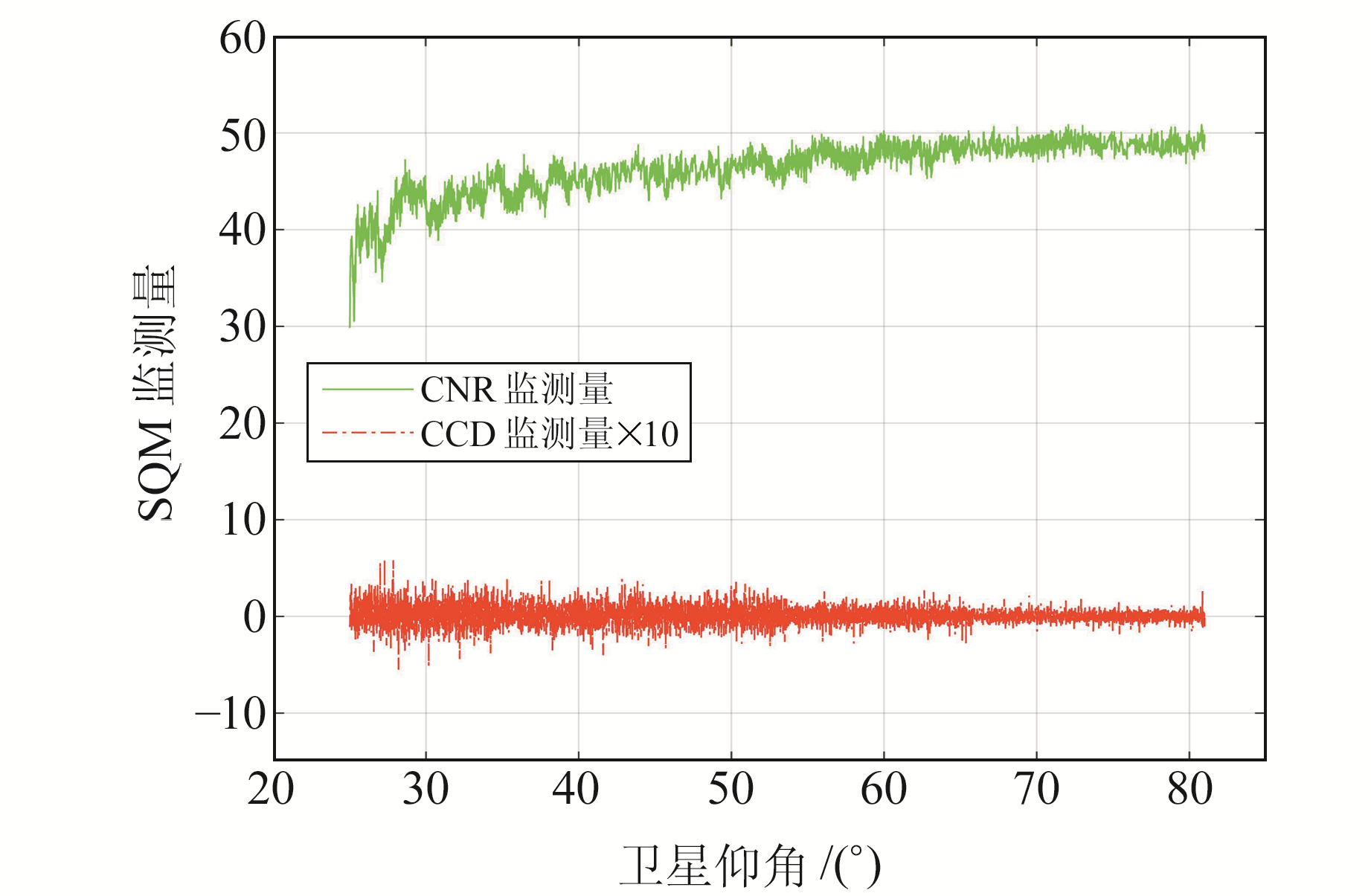
3 实验验证及分析 3.1 实验过程及数据拟合通过设置接收机使其长时间采集数据,模拟GBAS系统地面站的阈值建模过程,选取其中2 h的观测数据,根据式(1)和式(4)分别计算载噪比和CCD监测量。图 2为2 h观测过程中的可见卫星数,从图中可以看出,该时间段具有可观测的卫星来提供实验数据。选取GPS-28号卫星作为样本,图 3为其仰角对应的SQM监测量。
|
图 2 可见卫星数 Fig. 2 Number of visible satellites |
|
图 3 SQM监测量与对应卫星仰角 Fig. 3 SQM monitoring quantities and corresponding satellite elevation angle |
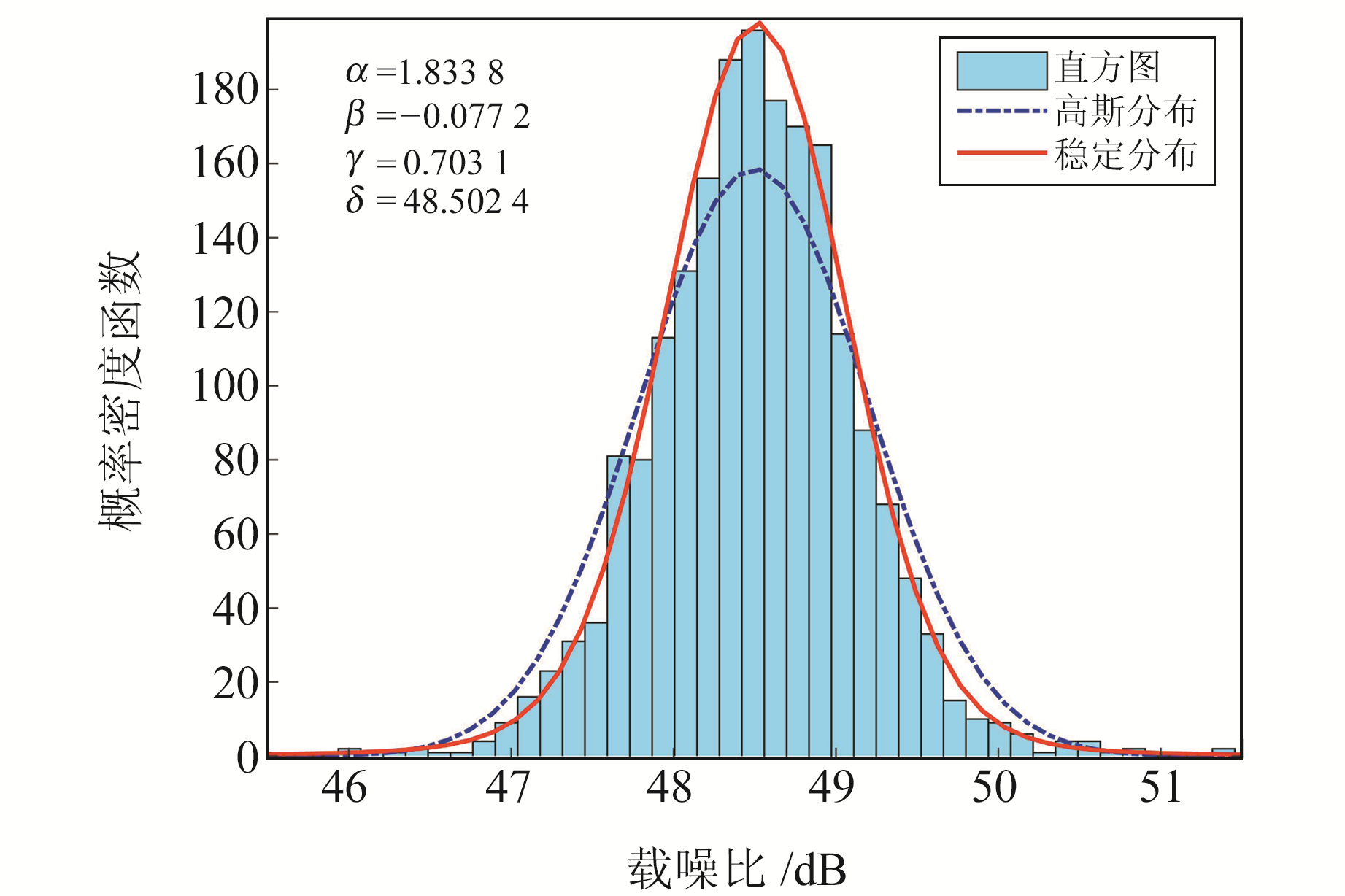
分别使用2种分布对GPS-28号卫星在65°~80°区间的载噪比监测量数据进行拟合,结果如图 4所示。从图中可以看出,对应参数下稳定分布曲线可以更好地包络载噪比数据直方图,能更加精确地描述载噪比的数据分布。
|
图 4 载噪比数据拟合 Fig. 4 CNR data fitting |
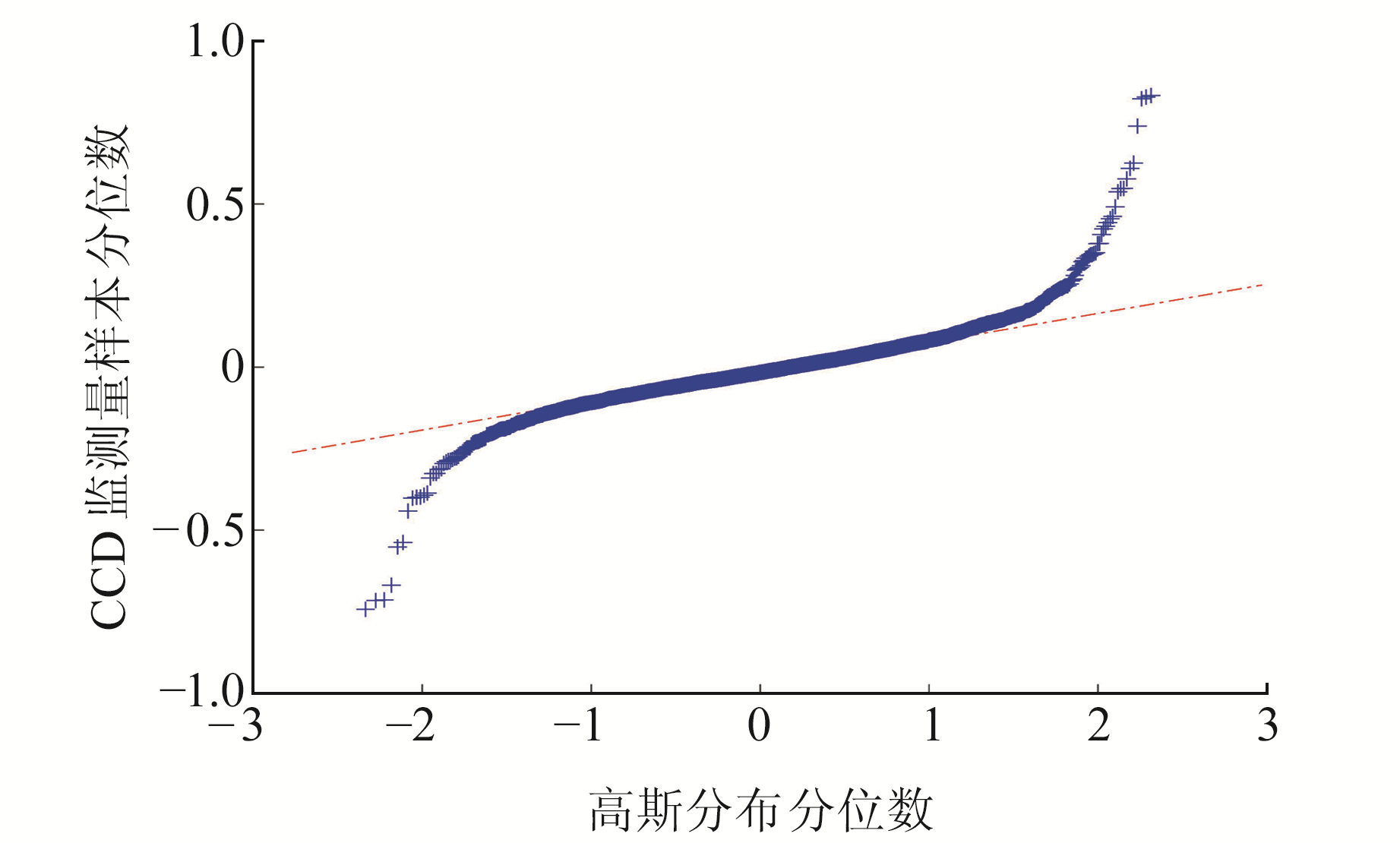
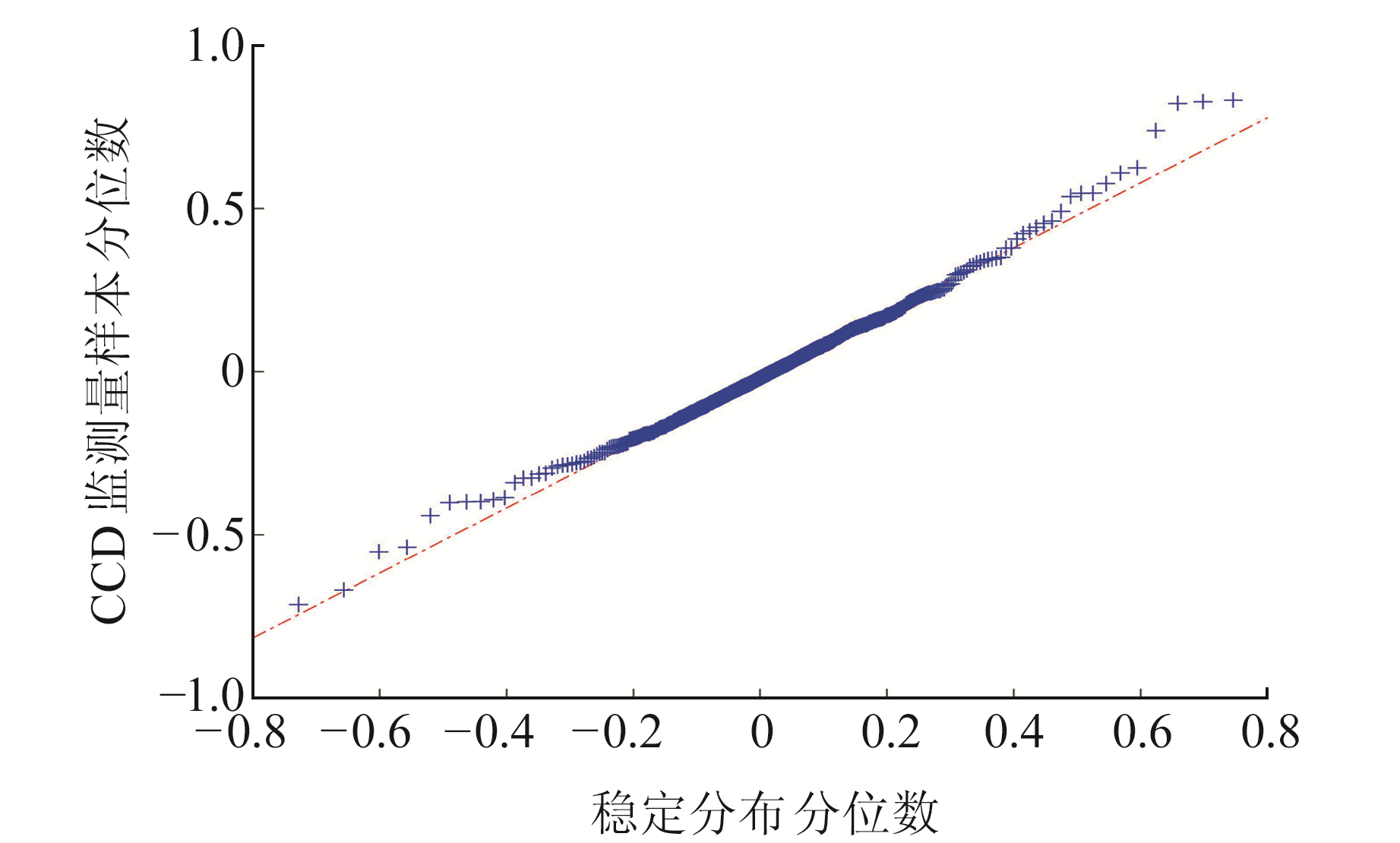
分别绘制GPS-28号卫星CCD监测量的高斯分布和稳定分布Q-Q图(分位数-分位数图),结果如图 5和图 6所示。从图中可以看出,CCD监测量与稳定分布更为一致,表明通过稳定分布对其阈值进行建模比高斯分布更加精确。
|
图 5 高斯分布下CCD样本Q-Q图 Fig. 5 Q-Q plot of CCD sample under Gaussian distribution |
|
图 6 稳定分布下CCD样本Q-Q图 Fig. 6 Q-Q plot of CCD sample under stable distribution |
表 1为CCD监测量在60°~80°区间的参数估计结果,从表中可以看出,稳定分布与载噪比和CCD监测量的分布更为一致,从而使阈值模型更加精确,可更加紧致地包络监测量。
|
|
表 1 CCD参数估计结果 Tab. 1 Estimation result of CCD parameters |
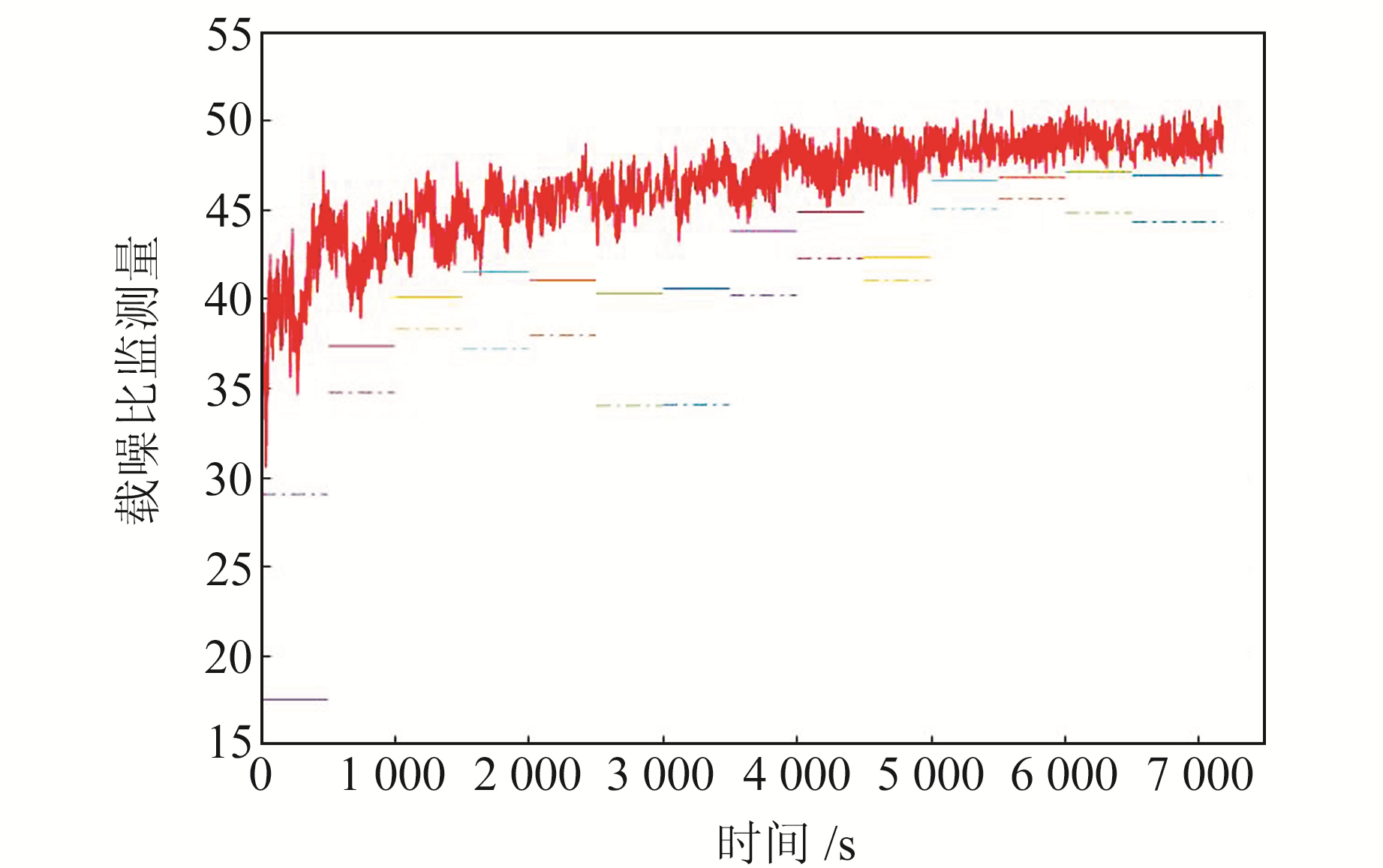
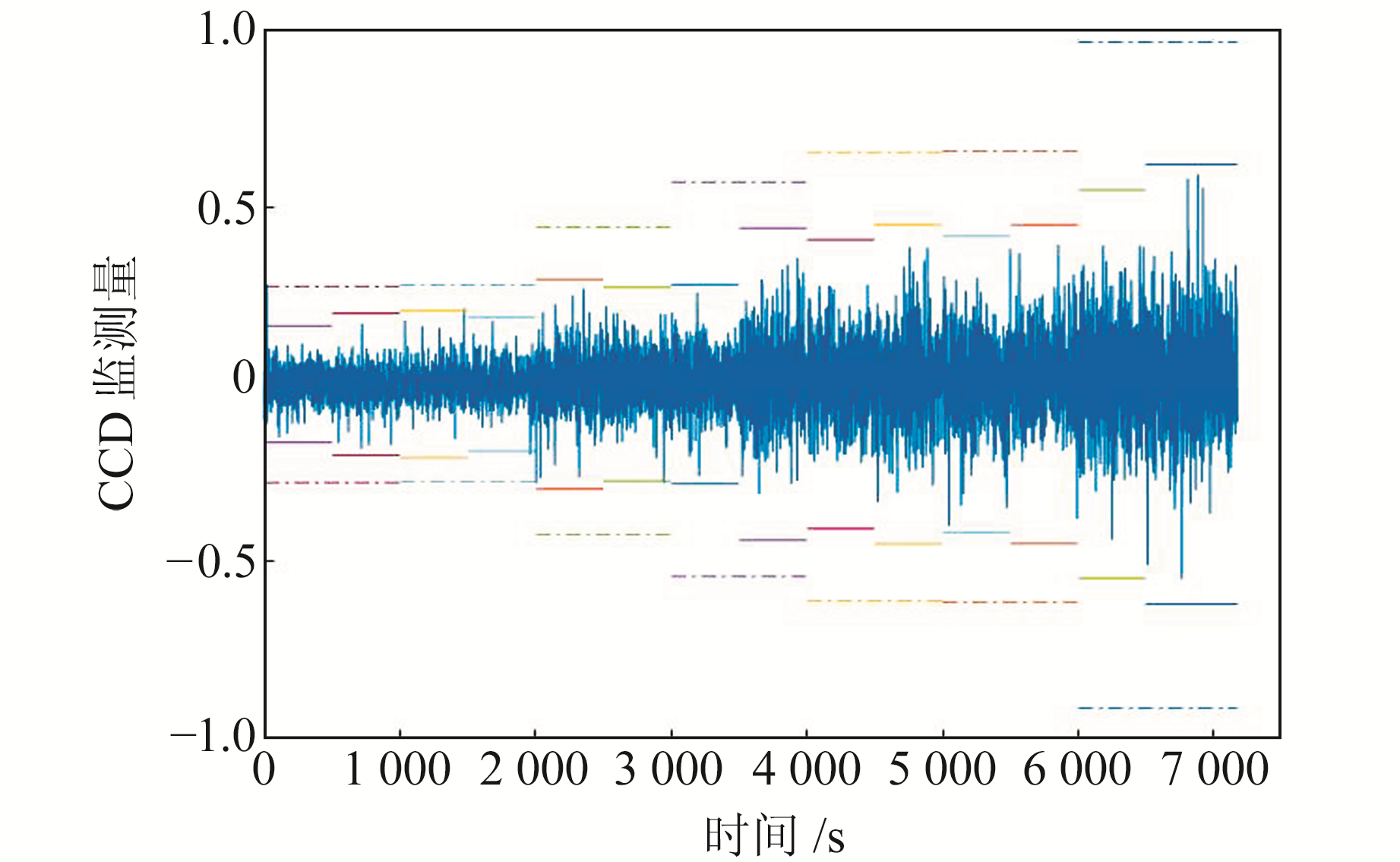
分别使用高斯分布和稳定分布对2个监测量样本进行建模,得到样本在观测时间内在不同仰角区间的阈值(图 7、图 8),图中实线部分为稳定分布模型下的阈值,虚线部分为高斯分布模型下的阈值。本次实验选择的GPS卫星在观测时间内仰角近似均匀变化且未出现换星情况,因此在作图过程中将时间作为横坐标。从图 7~8可以看出,稳定分布模型得到的阈值可以更紧致地包络SQM监测量,尤其是在高仰角部分效果更显著,因此稳定分布模型可以解决高斯分布过于保守而导致模型不准确的问题。
|
图 7 观测时段内载噪比及阈值 Fig. 7 CNR and threshold during observation time |
|
图 8 观测时段内CCD监测量及阈值 Fig. 8 CCD monitoring quantities and threshold during observation time |
表 2为通过2种分布计算的载噪比与CCD上限阈值均值,从表中可以看出,使用稳定分布模型得到的载噪比和CCD上限阈值比高斯分布模型分别提升和降低11.6%和35.7%,高精度的阈值模型在很大程度上可提高GBAS系统地面站监测过程的安全性。
|
|
表 2 两种分布计算的CCD/CNR阈值均值 Tab. 2 The average CCD/CNR threshold calculated by 2 methods |
本文提出一种稳定分布替代传统高斯分布,对GBAS系统地面站SQM监测过程中2个监测量进行建模及解算阈值的方法,并通过实验数据对该方法进行验证。结果表明,在载噪比和码/载波分歧监测过程中,稳定分布能更加准确地描述监测量,通过稳定分布建模得到的阈值可以更紧致地包络监测量,能解决高斯分布建模阈值精度低、过于保守的问题,提升GBAS系统地面站监测过程的可靠性。
| [1] |
刘海颖, 王惠南, 陈志明. 卫星导航原理与应用[M]. 北京: 国防工业出版社, 2013 (Liu Haiying, Wang Huinan, Chen Zhiming. Principle and Application of Satellite Navigation[M]. Beijing: National Defense Industry Press, 2013)
(  0) 0) |
| [2] |
López-Lago M, Serna J, Casado R, et al. Present and Future of Air Navigation: PBN Operations and Supporting Technologies[J]. International Journal of Aeronautical and Space Sciences, 2020, 21: 451-468 DOI:10.1007/s42405-019-00216-y
(  0) 0) |
| [3] |
Nikiforov I. From Pseudorange Overbounding to Integrity Risk Overbounding[J]. Navigation, 2019, 66(2): 417-439 DOI:10.1002/navi.303
(  0) 0) |
| [4] |
Jiang Y P, Milner C, Macabiau C. Code Carrier Divergence Monitoring for Dual-Frequency GBAS[J]. GPS Solutions, 2017, 21(2): 769-781 DOI:10.1007/s10291-016-0567-4
(  0) 0) |
| [5] |
Teunissen P J G, Montenbruck O. Springer Handbook of Global Navigation Satellite Systems[Z]. Cham: Springer International Publishing, 2017
(  0) 0) |
| [6] |
RTCA DO-245. Minimum Aviation System Performance Standards for the Local Area Augmentation System[S]. Washington: Radio Technical Commission for Aeronautics, 2004
(  0) 0) |
| [7] |
Molina-Muñoz J, Mora-Valencia A, Perote J. Market-Crash Forecasting Based on the Dynamics of the Alpha-Stable Distribution[J]. Physica A: Statistical Mechanics and Its Applications, 2020, 557: 124876 DOI:10.1016/j.physa.2020.124876
(  0) 0) |
| [8] |
Song G L, Guo X Y, Ma L. The Alpha Stable Distribution in Ocean Ambient Noise Modelling[C]. MATEC Web of Conferences, Wuhan, 2019
(  0) 0) |
| [9] |
Zarei S, Mohammadpour A, Ingrassia S, et al. On the Use of the Sub-Gaussian α-Stable Distribution in the Cluster-Weighted Model[J]. Iranian Journal of Science and Technology, Transactions A: Science, 2019, 43(3): 1059-1069 DOI:10.1007/s40995-018-0526-8
(  0) 0) |
| [10] |
Jin X H, Li X, Lu J Y. A Kernel Bound for Non-Symmetric Stable Distribution and Its Applications[J]. Journal of Mathematical Analysis and Applications, 2020, 488(2): 124063 DOI:10.1016/j.jmaa.2020.124063
(  0) 0) |
| [11] |
Nolan J P. Numerical Calculation of Stable Densities and Distribution Functions[J]. Communications in Statistics-Stochastic Models, 1997, 13(4): 759-774 DOI:10.1080/15326349708807450
(  0) 0) |
| [12] |
Xue R, Wang Z P, Zhu Y B. Upper Bound Estimation of Positioning Error for Ground-Based Augmentation System[J]. GPS Solutions, 2017, 21(4): 1781-1790 DOI:10.1007/s10291-017-0651-4
(  0) 0) |
| [13] |
李冬霞, 宋馥含, 刘瑞华. 北斗系统测距码与载波一致性评估与验证[J]. 系统仿真学报, 2018, 30(10): 949-3956 (Li Dongxia, Song Fuhan, Liu Ruihua. Assessment and Verification of Code-Carrier Coherence on BDS[J]. Journal of System Simulation, 2018, 30(10): 949-3956)
(  0) 0) |
| [14] |
Pu K. Using the Mixed Gaussian Distribution Method to Design of a Threshold for CCD Monitor[C]. 2013 International Conference on Communications, Circuits and Systems(ICCCAS), Chengdu, 2013
(  0) 0) |
2. State Key Laboratory of Air Traffic Management System and Technology, 8 Yongzhi Road, Nanjing 210016, China
 2021, Vol. 41
2021, Vol. 41

