南北两极常年被冰雪覆盖,对全球气候及环境变化具有重要影响。为能更好地对极地地区进行监测和探测,需要先进的导航定位技术,以全球定位系统(GPS)和北斗导航卫星系统(BDS)为代表的卫星导航定位系统相比于其他导航技术在极地地区具有明显优势[1]。
全球导航卫星系统(GNSS)在近几十年已取得快速发展,GLONASS性能日趋完善,Galileo和BDS都将在2020年年底实现全面运行,因此多模融合GNSS定位研究将成为主流。PPP技术是GNSS技术发展的重要里程碑,其无需用户自己设置地面基准站,可直接确定测站在国际地球参考框架下的高精度位置坐标。PPP技术在精密授时、低轨卫星精密定轨、GPS气象学、地球动力学等诸多地学研究及工程应用领域具有重要前景。近年来,随着多系统组合定位的发展,多模GNSS-PPP也取得重要发展。蔡昌盛等[2]系统性推理在GPS、GLONASS双系统下的无电离层PPP模型与UofC模型;张小红等[3]利用相应软件进行GPS/GLONASS双系统组合PPP解算;Li等[4]在原有GPS观测数据基础上增加BDS、GLONASS、Galileo观测数据,以提升PPP定位精度。
由于极地恶劣的生存环境和气候环境,对极地GNSS技术的研究较少,南极研究科学委员会于1994年组织了南极GPS联测[5]。Zhang等[6]通过GPS精密单点定位技术对Amery冰架前端观测点的水流速度进行监测;李伟伟等[7]利用GNSS数据探究南极区域的形变时序规律;杨元喜等[1]通过仿真分析对BDS导航卫星系统在极区的导航定位性能进行分析;左宗等[8]通过STK仿真软件对GNSS星座进行仿真,分析极地GNSS卫星覆盖性、可见性、高度角的变化规律。此外,杜玉军等[9]通过在南极采集的GPS和BDS实测数据分析了北斗在远洋及南极地区不同运动状态下的定位效果;周润杨[5]在Helmert方差分量估计的基础上提出一种极地BDS卫星分类的定权方法——PBCSH定权法;姚翔等[10]对极地环境下BDS三种轨道与GPS组合PPP的定位性能进行分析。
随着多模GNSS和PPP技术的发展,为更好地保障极地科考项目的顺利进行,确保极地考察的可靠性与安全性,极地多模PPP技术的研究意义重大。本文通过国际GNSS服务(IGS)提供的GNSS多系统试验网(multi-GNSS experiment,MGEX)的观测站数据进行多模精密单点定位解算,对极地环境下11种不同的导航卫星系统组合PPP的解算结果进行对比研究,分析在极地条件下多模PPP不同组合的差异和特征变化;通过收敛时间和定位误差分析极地环境下多模融合PPP的定位性能,为多模PPP在极地应用开展试探性研究。
1 PPP函数模型和数据处理策略 1.1 单系统PPP函数模型精密单点定位主要以测码伪距和载波相位作为基本观测量,本文主要采用传统的双频无电离层(ionosphere free, IF)组合观测值(以GPS为例):
| $ {P_{{\rm{IF}}}} = \rho _i^j + c\left( {d_{{t_i}}^j - d_t^j} \right) + T_i^j + M_i^j + b_{i/P}^j + {\varepsilon _{P/{\rm{F}}}} $ | (1) |
| $ \begin{array}{l} {\mathit{\Phi }_{{\rm{IF}}}} = \rho _i^j + c\left( {d_{{t_i}}^j - d_t^j} \right) + T_i^j + \\ \;{\lambda _{{\rm{IF}}}} \cdot {N_{{\rm{IF}}}} + M_i^j + b_{i/\mathit{\Phi }}^j + {\varepsilon _{\mathit{\Phi }/{\rm{IF}}}} \end{array} $ | (2) |
式中,PIF、ΦIF分别为GPS测码伪距与载波相位双频无电离层组合观测量,ρij为卫星到接收机的空间距离,c为真空中光速,dtij为接收机钟差,dtj为卫星钟差,Tij为对流层延迟,Mij为多路径误差,bi/Pj为接收机和卫星端伪距硬件延迟,bi/Φj为接收机和卫星端相位硬件延迟,λIF为双频无电离层组合的波长,NIF为双频无电离层组合的整周模糊度,εP/IF和εΦ/IF分别为消电离层测码伪距和载波相位观测值的噪声。
1.2 多系统融合PPP函数模型GPS、BDS、GLONASS、Galileo四个卫星系统在时间系统和坐标系统存在差异,所以多系统函数模型需要对其时间系统和坐标系统进行统一。在精密单点定位中精密卫星轨道产品可提供相同参考框架下不同卫星系统的卫星轨道产品,因此在进行双系统或多系统精密单点定位数据处理时不存在坐标转换问题[11]。对于时间系统的统一需要增加系统时间差tsys作为新的参数参与解算。
本文多系统融合的函数模型参考文献[5]、文献[10],未考虑南北极的差异变化(多路径效应、电离层延迟等)对卫星定位的差异性影响。
1.3 数据处理策略和实验方案本文选用4个能接收四系统卫星信号的观测站的数据进行实验,选取2020-01-01~01-05连续5 d的数据解算平差结果。由于所选的测站可接收北斗B1I和B2I频点信号,而BDS-3卫星只能接收B1I频点信号,故参与解算的BDS卫星均为BDS-2卫星。采用德国地学研究中心(GFZ)提供的精密星历和精密钟差产品,采用GAMP软件进行精密单点定位解算实验[12],以IGS发布的周解坐标为真值,详细的解算策略见表 1[8]。顾及到BDS轨道和钟差精度较低,将BDS载波相位和伪距观测值的测量误差比设置为1/500,其他系统均设置为1/100[13]。考虑到极地卫星高度角较低,因此本实验采用高度角定权的随机模型。本文主要采取两种方案:一天一站解和一天多站解[14]。对于一天一站解,主要选取CAS1站的数据进行所有双系统、三系统和四系统组合下的精密单点定位解算,得到观测站的定位结果。
|
|
表 1 极地多模GNSS精密单点定位解算策略 Tab. 1 Polar multi-GNSS PPP solution strategy |
极区复杂的观测环境使该地区的卫星信号受到严重干扰,为确保实验质量,需要对该地区的可用卫星情况进行评估。本文采用MGEX观测站的数据,选取CAS1、METG、OHI3和REYK四个观测站,分别对4种导航卫星系统的位置精度因子(PDOP)和卫星数进行分析(图 1)。

|
图 1 4个测站各导航卫星系统的卫星数和位置精度因子(PDOP) Fig. 1 Satellite number and PDOP value of navigation satellite systems at 4 stations |
由图 1(a)可知,在CAS1站,GPS的可见卫星数明显高于其他系统,可见卫星数超过10颗的历元数占总历元数60%(即1 d中有14.4 h);GLONASS、Galileo的最低可见卫星数分别为6颗、5颗;BDS的可见卫星数超过10颗的历元数占总历元数1.8%,最低为5颗;CAS1站4种系统的可见卫星数全天可用。从可靠性角度来看,GNSS的解算数据必须保证在观测时瞬时可用卫星数不少于5颗,PDOP值不大于6[15]。由图 1(b)可知,在METG站,GPS的可见卫星数仍高于其他系统,超过10颗的历元数占总历元数36%,最小为5颗;GLONASS、Galileo的最低可见卫星数分别为5颗、4颗,Galileo仅有4个历元不合格;BDS的卫星可见数最高为8颗,最低为2颗,且在2014历元之后无法接收到卫星信号,可见卫星数合格率为57%。相比于CAS1站,METG站的总体观测情况略差。除BDS外,其他卫星系统基本能满足全天观测。可见卫星数目低,可能是由于极地地区卫星高度角低,接收机无法接收到更多的卫星信号,以及极地复杂的气候环境对接收机天线的影响。图 1(c)为CAS1站4种导航卫星系统1 d内PDOP值的变化情况。从图中可以看出,GPS的波动范围最小;GLONASS次之;Galileo的波动范围较大,在1.509~8.521之间,PDOP值大于4的历元数占总历元数1.2%;BDS的波动范围最大,在1.673~17.175之间,PDOP值大于6的历元数占总历元数29.4%。由图 1(d)可知,在METG站,GPS的PDOP值仍然最稳定,GLONASS的PDOP值大于4的历元数占总历元数0.9%,Galileo的PDOP值大于4的历元数占总历元数7.5%,BDS的PDOP值波动范围较大,PDOP值小于6的历元数占总历元数40%。PDOP值的变化与可见卫星数密切相关,当卫星数增加时,卫星的网型会发生变化,从而影响PDOP值。图 1(e)和1(f)为BDS在OHI3站和REYK站的可见卫星数(其他系统的可见卫星数情况基本与CAS1站和METG站相同,故不作论述),从图中可以看出,OHI3站和REYK站BDS的可见卫星数全天均小于5颗,无法达到观测要求。通过对4种观测站的卫星数和PDOP值进行分析发现,在极地地区4种系统的观测条件存在差异,BDS与其他系统相差较大,主要原因为BDS-2的卫星数较少,无法完成全球覆盖。整体来看,所选观测站能够达到实验观测的基本要求。
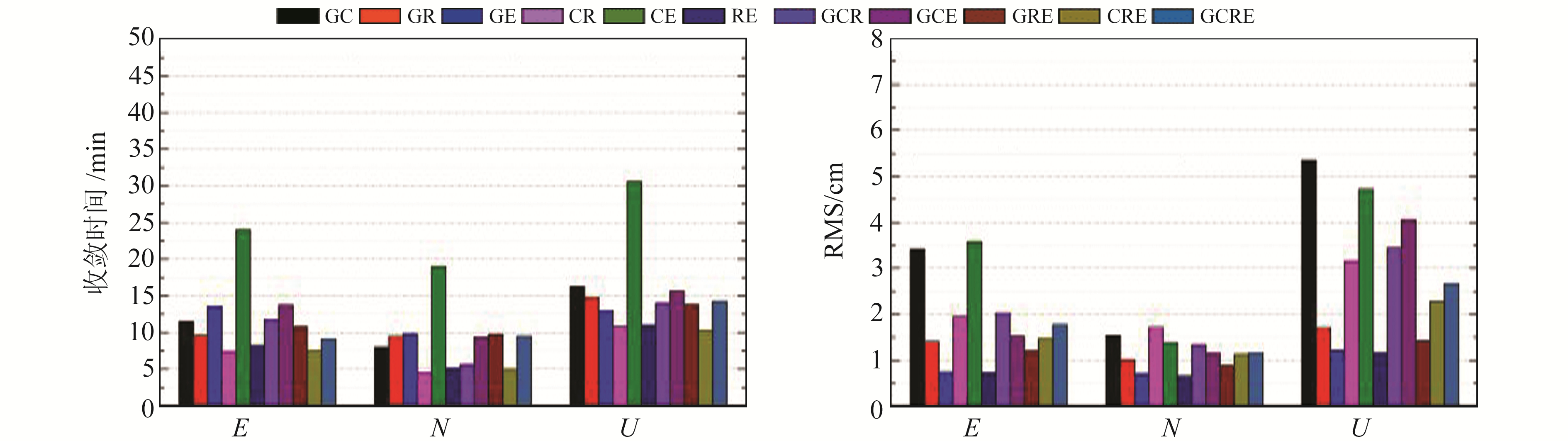
3 多模GNSS精密单点定位实验分析 3.1 一天一站解本实验主要是通过分析RMS和收敛时间研究CAS1站11种不同导航卫星系统组合PPP定位性能的规律性和差异性特征,为此给出11种不同导航卫星系统组合下PPP解的收敛时间(当定位误差达到10 cm并在连续历元内其定位误差优于10 cm所需的时间)和定位误差的均方根(RMS)。图 2为CAS1站11种不同组合下PPP解的收敛时间与定位误差的均方根(G表示GPS,C表示BDS,R表示GLONASS,E表示Galileo)。表 2和表 3分别为CAS1测站11种组合PPP的收敛时间和定位精度统计结果,表 4(表中“-”表示无对应的组合结果)为CAS1站三系统、四系统组合PPP较双系统组合PPP定位精度改善率的统计结果。
|
图 2 CAS1测站PPP收敛时间和定位误差均方根 Fig. 2 Convergence time and RMS of PPP at CAS1 station |
|
|
表 2 CAS1测站各系统组合PPP收敛时间 Tab. 2 Convergence time of PPP of each system combination at CAS1 station |
|
|
表 3 CAS1测站各系统组合PPP精度 Tab. 3 PPP accuracy of each system combination at CAS1 station |
|
|
表 4 CAS1站三系统、四系统组合PPP较双系统组合PPP定位精度改善率统计 Tab. 4 Statistics of positioning accuracy improvement rate of three-system and four-system combination PPP compared with two-system combination PPP at CAS1 station |
结合图 2、表 2和表 3可以看出,在收敛时间方面,N方向除CE组合外,其他系统组合的收敛时间均比E、U方向短,均优于10 min。这与导航卫星的运动轨迹密切相关,导航卫星所在的轨道面与赤道成一定夹角,导航卫星的运动轨迹大致为南北向,使得N方向网型结构变化较快,从而会加快N方向的收敛速度。GCE组合在E、N方向的收敛时间比GC组合延长2.2 min、1.3 min,CRE组合在E、N方向比CR组合延长3.5 min、5.2 min。可以看出,与双系统组合相比,三系统组合并未完全缩短收敛时间,部分甚至还会延长收敛时间。上述分析表明,在极地观测条件相同的情况下,多系统组合不一定能够缩短PPP收敛时间。
从定位精度来看,N方向和E方向整体优于U方向。双系统组合中GE、RE、GR组合的定位误差普遍小于CR、CE、GC组合,表明在极地地区BDS与其他导航卫星系统的组合效果较差。主要原因如下:实验中参与解算的仅有BDS-2卫星;BDS不同于其他导航卫星系统,其星座由3种不同类型的轨道组成,已有研究表明,不同轨道类型对PPP定位精度存在不同程度影响,这在一定程度上会影响BDS定位结果;BDS的卫星高度角偏低,受多路径影响较大。由表 4可知,GC、CR、CE组合在加入其他导航卫星系统后定位精度明显提升,GR、GE、RE组合在加入其他导航卫星系统后定位精度明显下降,表明在极区观测环境相同的条件下,多系统组合不一定能够提升PPP定位精度。
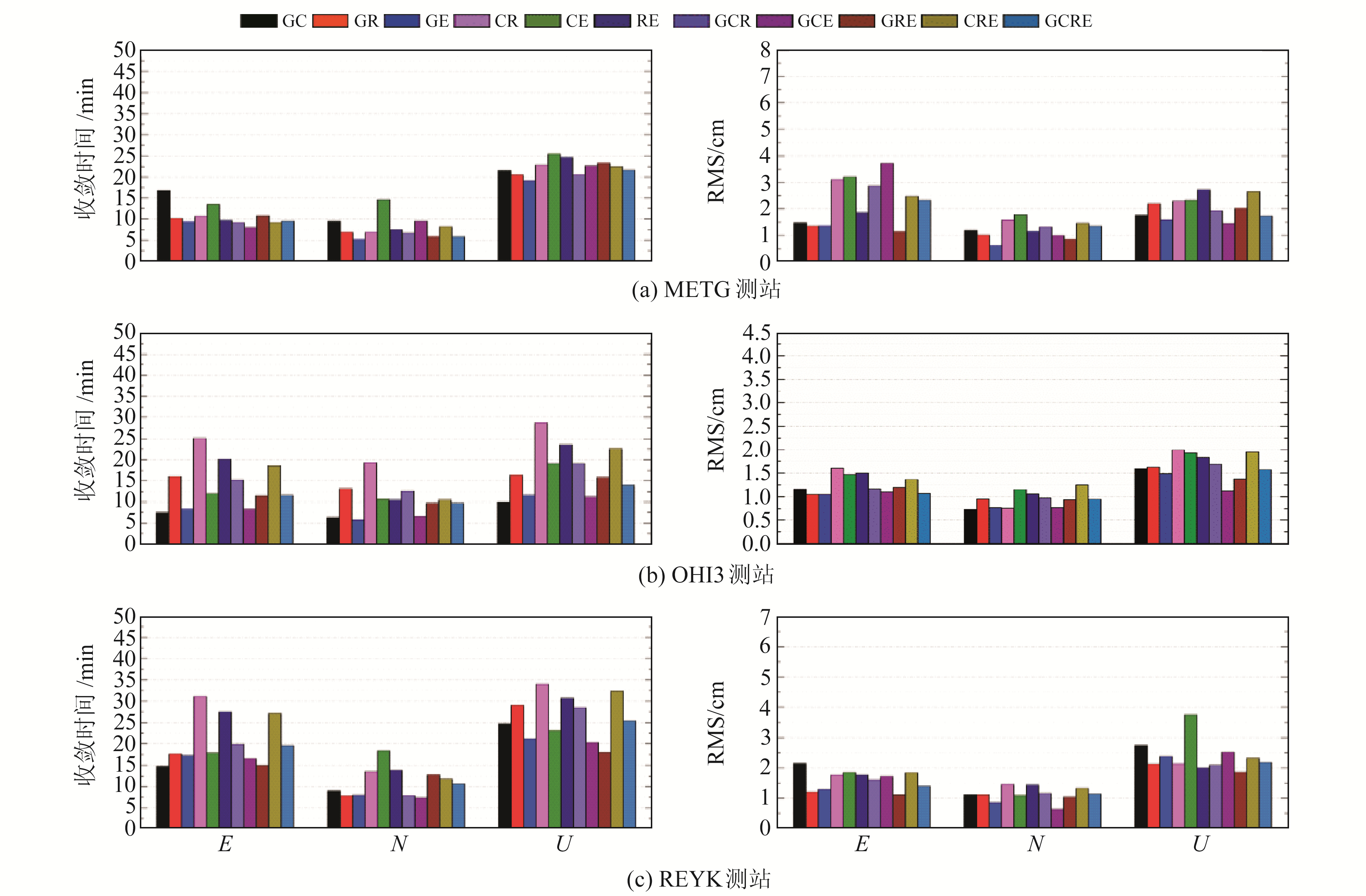
3.2 一天多站解本实验主要是为验证其他测站的定位性能是否与CAS1站具有相同特点,并研究其定位精度的差异。选取CAS1、METG、OHI3、REYK四个观测站进行PPP解算,采取的解算策略、精密产品、观测数据同§3.1。图 3为METG、OHI3、REYK三个观测站PPP收敛时间和定位误差均方根,表 5(单位min)和表 6(单位cm)分别为METG、OHI3、REYK三个观测站PPP收敛时间和定位误差均方根统计表。表 7为三系统组合PPP较双系统组合PPP定位精度改善率的统计结果,表 8为四系统组合PPP较三系统组合PPP定精度改善率的统计结果。
|
图 3 METG、OHI3、REYK观测站PPP收敛时间和定位误差均方根 Fig. 3 Convergence time and RMS of PPP at METG, OHI3, REYK stations |
|
|
表 5 不同组合下各测站PPP收敛时间统计 Tab. 5 Statistics of convergence time of PPP for different combinations |
|
|
表 6 不同组合下各测站PPP定位误差均方根统计 Tab. 6 RMS statistics of PPP for different combinations |
|
|
表 7 三系统组合PPP较双系统组合PPP定位精度改善率统计 Tab. 7 Statistics of positioning accuracy improvement rate of three-system combination PPP compared with two-system combination PPP |
|
|
表 8 四系统组合PPP较三系统组合PPP定位精度改善率统计 Tab. 8 Statistics of positioning accuracy improvement rate of four-system combination PPP compared with three-system combination PPP |
结合图 3及表 5和6可以看出,METG、OHI3、REYK三个观测站N方向收敛时间的平均值为7~11 min,定位精度的平均值优于1.3 cm,明显优于E方向和U方向。这与CAS1观测站一致,经综合研判认为主要与导航卫星的运动轨迹有关。由表 5可知,METG观测站收敛时间的平均值优于其他观测站,这是由于该站所在纬度相对较低,受极地地区对流层延迟、电离层延迟、多路径影响较小。由表 6可知,METG、OHI3、REYK三个观测站中CR、GC、CE组合在E、N、U三个方向的RMS值大部分优于CAS1观测站的相同组合,其中CR、GC组合相比于同测站的GE、RE、GR组合在不同方向上略有提高,其主要原因为CAS1观测站纬度最高。OHI3观测站三维点位误差的RMS值大于其他3个测站,主要原因为OHI3接收的BDS卫星平均为2~3颗,这在一定程度上会影响该测站多系统组合PPP的解算精度。METG、OHI3、REYK三个测站中CE组合三维点位误差的RMS值与平均值相比差值在0.4~1.3 cm之间,在所有组合中最大,这表明就定位精度而言,BDS与Galileo组合的效果最差。其主要原因在于,BDS-2卫星数较少,Galileo导航卫星系统也不完善。通过对4个观测站的定位精度进行对比分析发现,OHI3观测站的点位精度最高,CAS1观测站的点位精度最差。
结合表 7和8可以看出,各观测站的双系统组合和三系统组合在加入其他导航卫星系统后定位精度出现不同程度的升降变化,表明极地环境下多系统融合并不一定能提升PPP定位精度。同时分析发现,相同条件下基于BDS和Galileo组合的改善效率最好。从表 7可以看出,GE组合PPP的改善率多为负数,表明GE组合PPP定位精度的改善效果较差。从表 8可以看出,CRE、GCR组合在加入其他导航卫星系统后定位精度提升较为明显。
表 9为各观测站双系统组合的收敛时间和RMS平均值,表 10为各观测站三系统组合的收敛时间和RMS平均值。对比表 9和10可以发现,在收敛时间上三系统组合比双系统组合在E、N、U三个方向分别缩短10.3%、14.1%、7.3%,在定位精度上分别提升9.6%、4.6%、11.7%。结合表 5和6分析发现,在收敛时间上四系统组合比三系统组合在E、N、U三个方向分别缩短6.8%、-2.1%、2.0%,在定位精度上分别提升4.9%、-7.1%、5.3%。上述分析表明,在极地环境下三系统组合的定位性能优于双系统组合,四系统组合较三系统组合改善不明显。
|
|
表 9 各测站双系统组合收敛时间和RMS平均值 Tab. 9 The average values of convergence time and RMS of two-system combination |
|
|
表 10 各测站三系统组合收敛时间和RMS平均值 Tab. 10 The average values of convergence time and RMS of three-system combination |
鉴于极地复杂的气候环境以及多模GNSS-PPP技术的不断发展,本文通过相关实验对多模PPP的收敛时间和定位精度进行分析,研究极地环境下多模GNSS-PPP的定位性能,得出以下结论:
1) 对11种不同系统组合定位误差的RMS值进行分析发现,BDS与Galileo组合的定位效果较差,但在加入其他导航卫星系统后,改善效果比其他系统组合更为明显。这是因为BDS-2卫星的数量较少,无法达到全球覆盖,会严重影响北斗PPP的解算结果。
2) N方向收敛时间的平均值为7~11 min,定位精度的平均值优于1.3 cm,明显优于E方向和U方向。综合分析认为,其主要受卫星轨道的运行轨迹影响,卫星轨道倾角是以赤道为起始面,轨道倾角越大,卫星运行轨迹越接近南北方向,这会加速N方向卫星空间几何构型的变化,进而提升N方向的定位精度,并缩短收敛时间。
3) 在极地环境下三系统组合相较于双系统组合在定位性能上提升较为显著,在E、N、U三个方向的收敛时间分别缩短10.3%、14.1%、7.3%,在定位精度上分别提升9.6%、4.6%、11.7%。四系统组合的定位性能相较于三系统组合改善不明显。
| [1] |
杨元喜, 徐君毅. 北斗在极区导航定位性能分析[J]. 武汉大学学报: 信息科学版, 2016, 41(1): 15-20 (Yang Yuanxi, Xu Junyi. Navigation Performance of Beidou in Polar Area[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 15-20)
(  0) 0) |
| [2] |
蔡昌盛, 戴吾蛟, 匡翠林, 等. 利用UofC消电离层组合的GPS/GLONASS精密单点定位研究[J]. 武汉大学学报: 信息科学版, 2012, 37(7): 827-830 (Cai Changsheng, Dai Wujiao, Kuang Cuilin, et al. Study on GPS/GLONASS Precise Point Positioning Using UofC Ionosphere-Free Combination[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7): 827-830)
(  0) 0) |
| [3] |
张小红, 郭斐, 李星星, 等. GPS/GLONASS组合精密单点定位研究[J]. 武汉大学学报: 信息科学版, 2010, 35(1): 9-12 (Zhang Xiaohong, Guo Fei, Li Xingxing, et al. Study on Precise Point Positioning Based on Combined GPS and GLONASS[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 9-12)
(  0) 0) |
| [4] |
Li X X, Zhang X H, Ren X D, et al. Precise Positioning with Current Multi-Constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and Beidou[J]. Scientific Reports, 2015, 5(1): 8328 DOI:10.1038/srep08328
(  0) 0) |
| [5] |
周润杨. 极地BDS精密单点定位技术研究[D]. 郑州: 信息工程大学, 2017 (Zhou Runyang. Research on Precise Point Positioning Technology Based on BDS in Polar Regions[D]. Zhengzhou: Information Engineering University, 2017)
(  0) 0) |
| [6] |
Zhang X H, Andersen O B. Surface Ice Flow Velocity and Tide Retrieval of the Amery Ice Shelf Using Precise Point Positioning[J]. Journal of Geodesy, 2006, 80(4): 171-176 DOI:10.1007/s00190-006-0062-8
(  0) 0) |
| [7] |
李伟伟, 鞠晓蕾, 沈云中, 等. 联合GNSS和GRACE数据分析南极跟踪站的径向形变[J]. 极地研究, 2014, 26(2): 238-243 (Li Weiwei, Ju Xiaolei, Shen Yunzhong, et al. Vertical Deformation Analysis of Antarctic GNSS Stations Combined Using GNSS and GRACE Data[J]. Chinese Journal of Polar Research, 2014, 26(2): 238-243)
(  0) 0) |
| [8] |
左宗, 陈明剑. 极地GNSS性能仿真分析研究[J]. 全球定位系统, 2016, 41(5): 35-41 (Zuo Zong, Chen Mingjian. Simulation and Analysis of GNSS Performances Using STK in the Polar[J]. GNSS World of China, 2016, 41(5): 35-41)
(  0) 0) |
| [9] |
杜玉军, 王泽民, 安家春, 等. 北斗系统在远洋及南极地区的定位性能分析[J]. 极地研究, 2015, 27(1): 91-97 (Du Yujun, Wang Zemin, An Jiachun, et al. Positioning Analysis of Beidou Navigation Satellite System over Ocean and Antarctic Regions[J]. Chinese Journal of Polar Research, 2015, 27(1): 91-97)
(  0) 0) |
| [10] |
姚翔, 陈明剑, 李滢, 等. 极地BDS精密单点定位性能分析[J]. 导航定位学报, 2018, 6(4): 57-63 (Yao Xiang, Chen Mingjian, Li Ying, et al. Performance Analysis on Polar BDS PPP[J]. Journal of Navigation and Positioning, 2018, 6(4): 57-63)
(  0) 0) |
| [11] |
Cai C S, Gao Y, Pan L, et al. Precise Point Positioning with Quad-Constellations: GPS, Beidou, GLONASS and Galileo[J]. Advances in Space Research, 2015, 56(1): 133-143 DOI:10.1016/j.asr.2015.04.001
(  0) 0) |
| [12] |
邰贺. 基于GAMP软件的GNSS精密单点定位研究[J]. 测绘与空间地理信息, 2020, 43(2): 124-127 (Tai He. Research on GNSS Precise Point Positioning Based on GAMP Software[J]. Geomatics and Spatial Information Technology, 2020, 43(2): 124-127 DOI:10.3969/j.issn.1672-5867.2020.02.035)
(  0) 0) |
| [13] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[D]. 上海: 华东师范大学, 2018 (Zhou Feng. Theory and Methodology of Multi-GNSS Undifferenced and Uncombined Precise Point Positioning[D]. Shanghai: East China Normal University, 2018)
(  0) 0) |
| [14] |
陈泉余, 隋立芬, 田源, 等. BDS精密单点定位残差分析[J]. 测绘科学技术学报, 2017, 34(3): 240-244 (Chen Quanyu, Sui Lifen, Tian Yuan, et al. Analysis of Residuals of BDS Precise Point Positioning[J]. Journal of Geomatics Science and Technology, 2017, 34(3): 240-244)
(  0) 0) |
| [15] |
郭斐. GPS精密单点定位质量控制与分析的相关理论与方法研究[D]. 武汉: 武汉大学, 2013 (Guo Fei. Theory and Methodology of Quality Control and Quality Analysis for GPS Precise Point Positioning[D]. Wuhan: Wuhan University, 2013)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


