2. 南京航空航天大学航天学院,南京市御道街29号,210016;
3. 北京理工大学化学与化工学院,北京市中关村南大街5号,100081
基于捷联惯性导航系统/天文导航系统/全球导航卫星系统(SINS/CNS/GNSS)构成多传感器组合导航系统是目前研究较多的一种组合导航方式,其研究重点是以当地地理坐标系为基准的滤波方法[1-3],可广泛应用于航空、航天、航海等军用与民用领域。其中,捷联惯性导航系统为主导航设备,能够提供包括位置、速度、姿态等全导航参数;卫星导航系统能够提供长航时条件下较高精度的位置速度参数,并对导航计算机系统进行精确校时;天文导航系统能提供较高精度的姿态参数。利用GNSS、CNS可以不断校正捷联惯性导航系统初始对准、陀螺与加速度计漂移造成的导航误差,因此该组合导航系统具有显著优势,目前已有较多文献对具体算法模型和信息融合方法进行探讨,并取得较好的性能效果[4-8]。
同时,SINS/CNS/GNSS多传感器组合导航系统也是提高中远程弹道导弹命中精度的一种最具发展潜力的方法[9-10],但部分飞行载体(如导弹等)常用发射时刻的发射点惯性坐标系作为测量该载体飞行导航参数的基准,为此建立以发射惯性坐标系为基准的组合导航系统信息融合模型至关重要。
在现有的SINS误差建模研究中,一般均会考虑位置误差导致的引力误差项,但未具体分析该误差的量级与存在的必要性[6]。在测量误差模型方面,GNSS通常给出地固坐标系中的定位误差模型,但分析其在发射惯性坐标系中误差模型的研究较少,捷联系统的星敏感器可以根据QUEST等算法得出测量坐标系中的姿态误差协方差矩阵,但因IMU与星敏感器安装方位的关系、地心惯性坐标系与发射惯性坐标系的转换等因素,也需要研究最终的定姿误差模型。另外,现有研究通常根据姿态误差角与数学平台失准角之间的数学关系和星敏感器姿态测量值来估计SINS的数学平台失准角[7, 11],但过程较为复杂。
为此,本文推导基于发射惯性坐标系下的组合导航系统滤波的状态方程与量测方程,并针对目前该配置的组合导航算法存在的不足提出一种优化的组合导航滤波模型和测量噪声模型,最后进行较为细致的仿真验证。
1 组合导航系统建模 1.1 状态方程在地心惯性坐标系中,比力方程可以描述为:
| $ {\mathit{\boldsymbol{f}}_i} = {\mathit{\boldsymbol{\dot \upsilon }}_i} - \mathit{\boldsymbol{g}}{} $ | (1) |
式中,fi、
对式(1)进行如下变换:
| $ \mathit{\boldsymbol{C}}_b^g\mathit{\boldsymbol{C}}_i^b{\mathit{\boldsymbol{f}}_i} = \mathit{\boldsymbol{C}}_b^g{\mathit{\boldsymbol{f}}_b} = \mathit{\boldsymbol{C}}_i^{\rm{g}}{\mathit{\boldsymbol{\dot v}}_i} - \mathit{\boldsymbol{C}}_i^{\rm{g}}\mathit{\boldsymbol{g}} $ | (2) |
式中,上标或下标g、i、b分别代表发射惯性坐标系、地心惯性坐标系、本体坐标系;Cgb为本体坐标系相对于发射惯性坐标系的姿态矩阵;Cib为本体坐标系相对于地心惯性坐标系的姿态矩阵;fb(= Cibfi)为加速度计输出的真值;Cig为发射惯性坐标系相对于地心惯性坐标系的姿态矩阵;g为地球引力加速度,因为弹道高度和地球扁率对引力影响相对较大,因此引力加速度可考虑中心引力和J2摄动两部分。
由于本文采用的导航坐标系为发射惯性坐标系,令式(2)中
| $ \mathit{\boldsymbol{C}}_b^{\rm{g}}{\mathit{\boldsymbol{f}}_b} = \mathit{\boldsymbol{\dot v}} - \mathit{\boldsymbol{C}}_i^{\rm{g}}\mathit{\boldsymbol{g}} $ | (3) |
位置可由速度直接积分得到:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot p}} = \mathit{\boldsymbol{\upsilon }}} \end{array} $ | (4) |
式中,p、υ分别为载体在发射惯性坐标系中的位置和速度。采用四元数描述载体相对于发射惯性坐标系的姿态运动,可避免姿态运算过程中的奇异点,基于陀螺角速度测量值积分推算下时刻的载体姿态:
| $ \mathit{\boldsymbol{\dot q}} = 0.5 \cdot \mathit{\boldsymbol{q}} \circ {\mathit{\boldsymbol{\omega }}_b} $ | (5) |
式中,q为载体相对于发射惯性坐标系的姿态四元数,ωb为载体角速度。由于在发射惯性坐标系中飞行器工作时间均较短,陀螺与加速度计的测量误差可简化建模为“随机游走+白噪声”形式[8],即
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\omega }}_c} = {\mathit{\boldsymbol{\omega }}_b} + {\mathit{\boldsymbol{\omega }}_r} + {\mathit{\boldsymbol{\omega }}_\varepsilon }}\\ {{{\mathit{\boldsymbol{\dot \omega }}}_r} = {\mathit{\boldsymbol{\omega }}{}_n}} \end{array}} \right. $ | (6) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{f}}_c} = {\mathit{\boldsymbol{f}}_b} + {\mathit{\boldsymbol{f}}_r} + {\mathit{\boldsymbol{f}}_\varepsilon }}\\ {{{\mathit{\boldsymbol{\dot f}}}_r} = {\mathit{\boldsymbol{f}}_n}} \end{array}} \right. $ | (7) |
式中,ωb、fb分别为陀螺、加速度计测量值;ωr、fr分别为陀螺、加速度计随机游走误差;ωn、fn分别为陀螺、加速度计随机游走驱动噪声;ωε、fε分别为陀螺、加速度计测量噪声,可看作白噪声。
1.2 测量方程由于GNSS测量值一般基于地固坐标系,因此需要考虑极移、时角、章动和岁差等变换,最终得到在发射惯性坐标系下的定位值,则测量方程可表示为:
| $ {\boldsymbol{p}_c} = \boldsymbol{C}_i^g\boldsymbol{C}_e^i \cdot {\boldsymbol{p}_g} - \boldsymbol{C}_i^g{\boldsymbol{R}_o} + \boldsymbol{C}_i^g\boldsymbol{C}_e^i \cdot {\boldsymbol{p}_\varepsilon } $ | (8) |
式中,上标或下标e代表地固坐标系,Cei为接收机定位时刻地心惯性坐标系相对于地固坐标系的姿态矩阵,Ro为发射惯性坐标系原点在地心惯性坐标系下的数值,pε为接收机在地固坐标系中的定位误差模型,pg为接收机在地固坐标系中的定位信息。
一般来说,捷联系统的星敏感器测量的是传感器相对于地心惯性坐标系的姿态,而导航解算时需要载体相对于发射惯性坐标系的姿态参数;同时,IMU和星敏感器之间的相对姿态也需要事前精确标定,因此基于星敏感器的姿态测量方程可表示为:
| $ \begin{array}{l} \;\;\;{\boldsymbol{q}_c} = \boldsymbol{q}_g^{ - 1} \circ {\boldsymbol{q}_s} \circ {\boldsymbol{q}_\varepsilon } \circ {\boldsymbol{q}_f} = {\boldsymbol{q}^t} \circ {\boldsymbol{q}_\varepsilon } \circ {\boldsymbol{q}_f} = \\ \left( {{\boldsymbol{q}^t} + \boldsymbol{q}_\varepsilon ^1} \right) \circ {\boldsymbol{q}_f} = {\boldsymbol{q}^t} \circ {\boldsymbol{q}_f} + \boldsymbol{q}_\varepsilon ^1 \circ {\boldsymbol{q}_f} = \boldsymbol{q} + {\boldsymbol{q}_\eta } \end{array} $ | (9) |
式中,qg为发射惯性坐标系相对于地心惯性坐标系的姿态四元数,qf为IMU测量坐标系相对于CNS测量坐标系的姿态四元数,qs为星敏感器姿态真值,qε为星敏感器的测量噪声。另外,如果采用QUEST算法处理多矢量定姿问题,可直接获得姿态误差协方差阵的估计:
| $ \begin{array}{l} \boldsymbol{q} = \boldsymbol{q}_g^{ - 1} \circ {\boldsymbol{q}_s} \circ {\boldsymbol{q}_f}\\ {\boldsymbol{q}_t} = \boldsymbol{q}_g^{ - 1} \circ {\boldsymbol{q}_s}\\ \boldsymbol{q}_\varepsilon ^1 = \left[ {\begin{array}{*{20}{l}} { - q_1^t{q_{\varepsilon 1}} - q_2^t{q_{\varepsilon 2}} - q_3^t{q_{\varepsilon 3}}}\\ { + q_0^t{q_{\varepsilon 1}} - q_3^t{q_{\varepsilon 2}} + q_2^t{q_{\varepsilon 3}}}\\ { + q_3^t{q_{\varepsilon 1}} + q_0^t{q_{\varepsilon 2}} - q_1^t{q_{\varepsilon 3}}}\\ { - q_2^t{q_{\varepsilon 1}} + q_1^t{q_{\varepsilon 2}} + {q_0}{q_{\varepsilon 3}}} \end{array}} \right]\\ {\boldsymbol{q}_\eta } = \boldsymbol{q}_\varepsilon ^1 \circ {\boldsymbol{q}_f} \end{array} $ | (10) |
由§1可知,该导航系统的数学模型具有非线性特性,可设计扩展卡尔曼滤波器进行信息融合计算。首先根据上述状态方程、测量方程推导相应的误差增量方程,然后建立扩展卡尔曼滤波器模型。
2.1 误差增量方程推导利用角运动方程式(5)求解误差增量方程,模型推导过程中姿态四元数误差为SINS预报姿态误差,而不是通常使用的数学平台失准角,结合姿态测量方程可获得更简洁的姿态估计模型。由于四元数中4个元素不独立,因此可忽略姿态四元数的标量部分,并考虑陀螺随机游走误差和随机噪声。
对角运动求取微分增量方程,并忽略姿态四元数的标量部分[12],则:
| $ \delta {\boldsymbol{\dot q}_{13}} = - [\boldsymbol{\dot \omega } \times ] \cdot \delta {\boldsymbol{q}_{13}} + 0.5 \cdot \delta \boldsymbol{\omega } $ | (11) |
式中,δω包含两部分误差,第一部分为陀螺随机游走误差,第二部分为陀螺噪声。对上述方程进一步展开,则:
| $ \delta {\boldsymbol{\dot q}_{13}} = - [\boldsymbol{\hat \omega } \times ] \cdot \delta {\boldsymbol{q}_{13}} - 0.5 \cdot {\boldsymbol{\omega }_r} - 0.5 \cdot {\boldsymbol{\omega }_\varepsilon } $ | (12) |
式中,
对式(3)进行误差增量方程推导,主要考虑姿态误差、加速度计误差,首先推导方程左侧,则:
| $ \boldsymbol{C}_b^g{\boldsymbol{f}_b} = \left( {\boldsymbol{C}_b^g \cdot \delta \boldsymbol{C}_b^g} \right) \cdot {\boldsymbol{f}_c} $ | (13) |
由姿态四元数可直接得到Cbg,则[13]:
| $ \delta \boldsymbol{C}_b^g = \left[ {\begin{array}{*{20}{c}} 1&{ - 2\delta {q_3}}&{2\delta {q_2}}\\ {2\delta {q_3}}&1&{ - 2\delta {q_1}}\\ { - 2\delta {q_2}}&{2\delta {q_1}}&1 \end{array}} \right] $ |
式(13)可继续改写为:
| $ \begin{array}{l} \boldsymbol{C}_b^g{\boldsymbol{f}_b} \approx \boldsymbol{C}_b^g \cdot \left( {{{\boldsymbol{\hat f}}_b} - {\boldsymbol{f}_r} - {\boldsymbol{f}_\varepsilon }} \right) + \\ \boldsymbol{C}_b^{\rm{g}} \cdot \left[ {\begin{array}{*{20}{c}} 0&{ - 2\delta {q_3}}&{2\delta {q_2}}\\ {2\delta {q_3}}&0&{ - 2\delta {q_1}}\\ { - 2\delta {q_2}}&{2\delta {q_1}}&0 \end{array}} \right] \cdot {{\boldsymbol{\hat f}}_b} = \\ \boldsymbol{C}_b^g \cdot {{\boldsymbol{\hat f}}_b} - \boldsymbol{C}_b^g \cdot {\boldsymbol{f}_r} - \boldsymbol{C}_b^g \cdot {\boldsymbol{f}_\varepsilon } + 2\boldsymbol{C}_b^g \cdot \left[ {{{\boldsymbol{\hat f}}_b} \times } \right] \cdot \delta {\boldsymbol{q}_{13}} \end{array} $ | (14) |
式中,
| $ \left[ {{{\boldsymbol{\hat f}}_b} \times } \right] = \left[ {\begin{array}{*{20}{c}} 0&{ - {{\hat f}_{bz}}}&{{{\hat f}_{by}}}\\ {{{\hat f}_{bz}}}&0&{ - {{\hat f}_{bx}}}\\ { - {{\hat f}_{by}}}&{{{\hat f}_{bx}}}&0 \end{array}} \right] $ |
对于式(3)右侧
| $ \boldsymbol{g} = \left[ \begin{array}{l} - \frac{{\mu x}}{{{r^3}}}\left[ {1 - {J_2}{{\left( {\frac{{{R_e}}}{r}} \right)}^2}\left( {7.5\frac{{{z^2}}}{{{r^2}}} - 1.5} \right)} \right]\\ - \frac{{\mu y}}{{{r^3}}}\left[ {1 - {J_2}{{\left( {\frac{{{R_e}}}{r}} \right)}^2}\left( {7.5\frac{{{z^2}}}{{{r^2}}} - 1.5} \right)} \right]\\ - \frac{{\mu z}}{{{r^3}}}\left[ {1 - {J_2}{{\left( {\frac{{{R_e}}}{r}} \right)}^2}\left( {7.5\frac{{{z^2}}}{{{r^2}}} - 4.5} \right)} \right] \end{array} \right] $ | (15) |
式中,μ=3.986×1014、J2=1.083×10-3、Re=6 378 137 m,(x, y, z)为载体的空间位置坐标,r为载体到地心的距离。
对式(15)进行分析,则:
| $ 0 < \left[ {1 - {J_2}{{\left( {\frac{{{R_e}}}{r}} \right)}^2}\left( {7.5\frac{{{z^2}}}{{{r^2}}} - 4.5} \right)} \right] < 1 $ |
因此,该处采用
| $ - \frac{\mu }{{{r^3}}}{\rm{d}}x + 3\frac{{\mu {x^2}}}{{{r^5}}}{\rm{d}}x + 3\frac{{\mu xy}}{{{r^5}}}{\rm{d}}y + 3\frac{{\mu xz}}{{{r^5}}}{\rm{d}}z $ |
假定误差为100 m(在GPS正常情况下不可能存在的误差),设定r=6 400 km,则误差量级为10-4 m·s-2,若考虑仪器精度为10-4 g,则完全可忽略地球引力g的影响。忽略该项误差后,则:
| $ \boldsymbol{\dot v} - \boldsymbol{C}_i^g\boldsymbol{g} = \widehat {\boldsymbol{\dot v}} + \delta \boldsymbol{\dot v} - \boldsymbol{C}_i^g\boldsymbol{g} $ | (16) |
式中,
| $ \delta \boldsymbol{\dot v} = 2\boldsymbol{C}_b^{\rm{g}} \cdot \left[ {{{\boldsymbol{\hat f}}_b} \times } \right] \cdot \delta {\boldsymbol{q}_{13}} - \boldsymbol{C}_b^{\rm{g}} \cdot \delta {\boldsymbol{f}_r} - \boldsymbol{C}_b^{\rm{g}} \cdot {\boldsymbol{f}_\varepsilon } $ | (17) |
则GPS的位置误差增量方程为:
| $ {\boldsymbol{p}_c} - \boldsymbol{\hat p} = \delta \boldsymbol{p} + \boldsymbol{C}_i^{\rm{g}}\boldsymbol{C}_e^i \cdot {\boldsymbol{p}_\varepsilon } $ | (18) |
根据四元数理论,通过计算四元数的误差四元数可得到星敏感器的姿态误差增量方程为[14]:
| $ {\left( {{{\boldsymbol{\hat q}}^{ - 1}} \circ {\boldsymbol{q}_c}} \right)_{13}} = \delta {\boldsymbol{q}_{13}} + {\left( {{{\boldsymbol{\hat q}}^{ - 1}} \circ {\boldsymbol{q}_\eta }} \right)_{13}} $ | (19) |
式中,
通过对SINS、CNS与GNSS在发射惯性坐标系中的导航模型、性能和误差源进行分析,最终可得到三组合导航系统的信息融合模型:
| $ \boldsymbol{\dot X}(t) = \boldsymbol{F}(t)\boldsymbol{X}(t) + \boldsymbol{G}(t)\boldsymbol{W}(t) $ | (20) |
| $ \boldsymbol{Z}(t) = \boldsymbol{H}(t)\boldsymbol{X}(t) + \boldsymbol{V}(t) $ | (21) |
| $ \boldsymbol{X} = \left[ {\begin{array}{*{20}{l}} {\delta {\boldsymbol{q}_{13}}}&{\delta \boldsymbol{p}}&{\delta \boldsymbol{v}}&{{\boldsymbol{\omega }_r}}&{{\boldsymbol{f}_r}} \end{array}} \right] $ | (22) |
式中,δq13为姿态四元数误差的矢量部分,δp为位置误差,δv为速度误差,ωr为陀螺随机游走误差,fr为加速度计的随机游走误差,共15维。对式(17)、(18)所建立的组合导航系统的状态方程和量测方程进行离散化处理后,即可利用间接卡尔曼滤波器对惯性导航误差进行最优估计和修正[9]。
在上述系统模型中,根据式(21)、(22)可得到与式(18)对应的发射惯性坐标系下GNSS/SINS组合子系统的量测方程为:
| $ {\boldsymbol{Z}_G}(t) = {\boldsymbol{H}_G}(t)\boldsymbol{X}(t) + {\boldsymbol{V}_G}(t) $ | (23) |
式中,
根据式(21)、(22)可得到与式(19)对应的发射惯性坐标系下CNS/SINS组合子系统的量测方程为:
| $ {\boldsymbol{Z}_C}(t) = {\boldsymbol{H}_C}(t)\boldsymbol{X}(t) + {\boldsymbol{V}_C}(t) $ | (24) |
式中,
利用该实验验证本文提出的GNSS和CNS测量噪声误差模型的正确性。飞行器的发射地点位于发射坐标系的坐标原点,飞行轨迹设为0~50 s以5 m/s2加速垂直上升,51~110 s匀速垂直上升,111~220 s以0.5°/s角加速度转弯,221~600 s以5 m/s2倾斜加速爬升,601~670 s以0.5°/s角加速度转弯,671~900 s匀速平飞。其飞行轨迹如图 1所示。
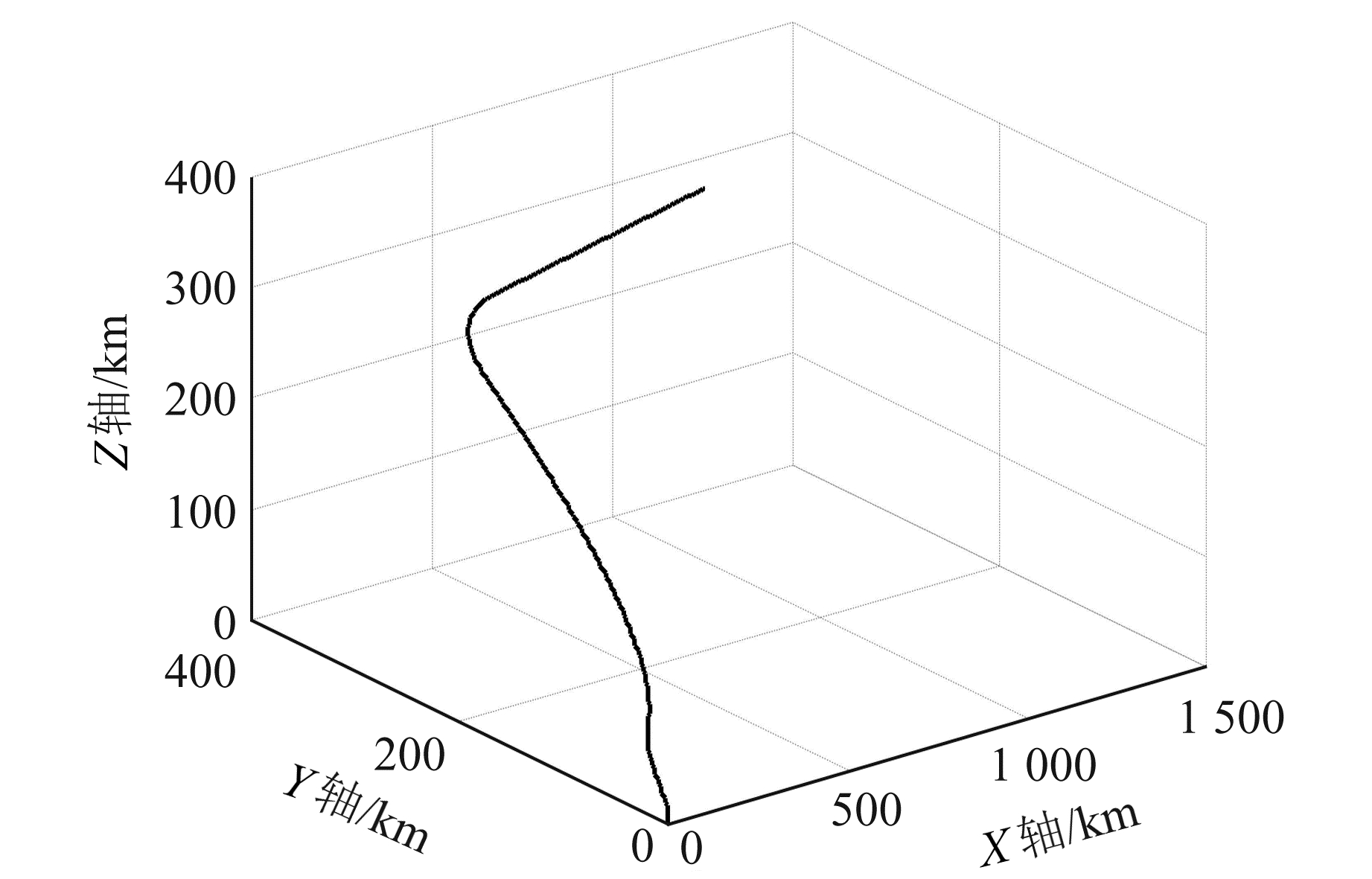
|
图 1 飞行轨迹 Fig. 1 Flight path |
飞行过程中,设定GNSS在地固坐标系中的三轴随机误差均为10 m(1 σ),令星敏感器在地心惯性坐标系下的三轴姿态随机误差均为10″(1 σ),图 2中实线为GNSS在发射惯性坐标系下各历元的定位误差,虚线为理论定位误差3 σ包络线(30 m),其可较好地包络误差,从而验证本文提出的GNSS测量误差模型的正确性。同时,本文设置的3个方向的随机误差量级相同,而姿态转换矩阵为正交矩阵,所以导致GNSS在发射惯性坐标系中的噪声与其在地固坐标系一致。图 3中实线为星敏感器各历元的测量误差曲线,虚线为理论上对应3个误差的3 σ包络线,也能较好地拟合误差,表明姿态测量误差模型的正确性,有利于保证信息融合的最优性。

|
图 2 GNSS定位误差 Fig. 2 GNSS positioning error |

|
图 3 CNS定姿误差 Fig. 3 CNS attitude error |
利用本实验综合验证简洁导航数学模型与融合算法。设定惯性导航系统的等效陀螺漂移的驱动噪声为0.1°/h,白噪声也为0.1°/h,等效加速度计漂移的驱动噪声为10-4 g,白噪声也为10-4 g;捷联惯性导航系统的解算周期为20 ms,GNSS和CNS的输出周期均为1 s;捷联惯性导航系统的三轴姿态初始误差设为30″,GNSS在地固坐标系下的三轴随机误差均为10 m(1 σ),星敏感器在地心惯性坐标系下的三轴姿态随机误差[1, 12]均为10″(1 σ)。发射惯性坐标系建立在发射原点,因此位置初值直接设为0。
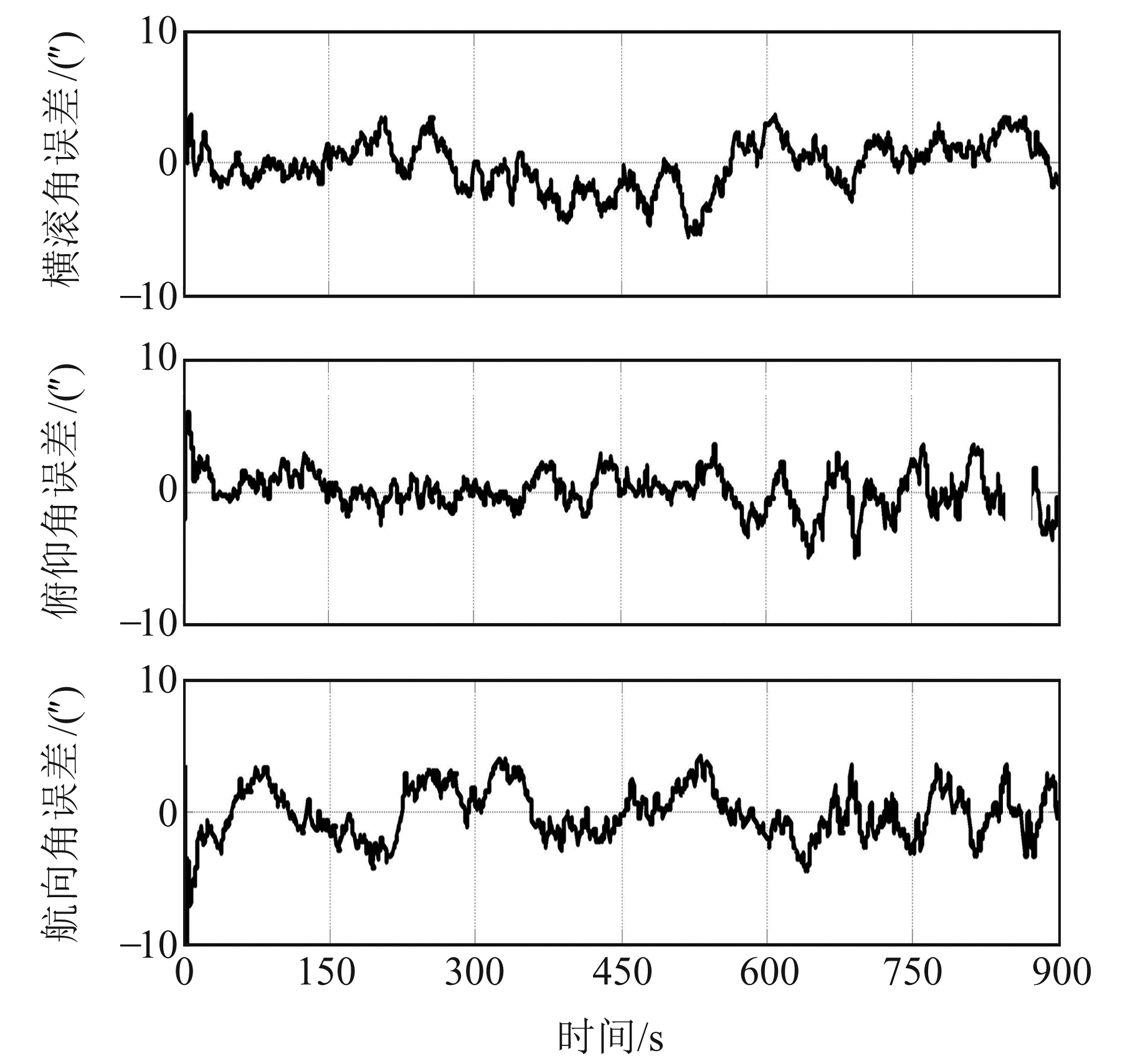
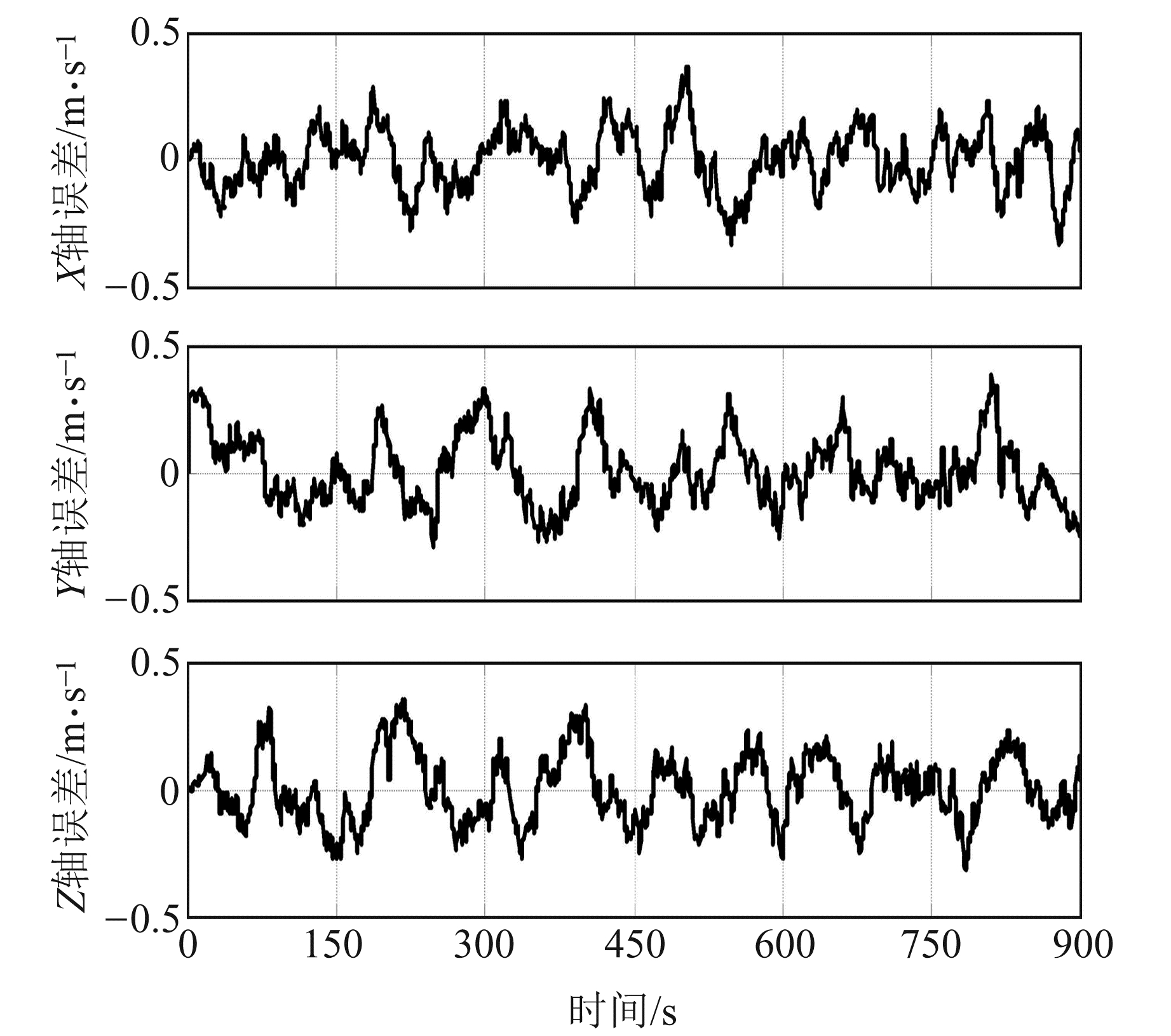
将组合导航系统输出的姿态角、位置、速度与根据图 1航迹得到的真实姿态角、位置、速度进行比较,得到如图 4~6所示的各导航参数误差曲线。为了更形象、直观地分析上述结果,根据仿真数据,得到各类导航参数误差的统计结果(表 1)。
|
图 4 姿态误差 Fig. 4 Attitude error |

|
图 5 位置误差 Fig. 5 Position error |
|
图 6 速度误差 Fig. 6 Velocity error |
|
|
表 1 各导航参数误差统计分析 Tab. 1 Statistical analysis of navigation parameters error |
由图 4~6及表 1可以看出,系统模型稳定,精度较高,能够满足实际应用需求。
4 结语捷联惯性导航系统/天文导航系统/卫星定位系统构成的组合导航系统具有较好的性能和应用前景。本文推导基于发射惯性坐标系下组合导航系统滤波的状态方程与量测方程;并针对目前该组合导航算法存在的不足,提出一种优化的组合导航滤波模型和测量噪声模型;最后通过较为细致的仿真实验验证本文方法的正确性和有效性。
在GNSS对应的量测方程式(20)中,仅考虑了GNSS提供的位置信息而未考虑速度信息,这是因为本文目的是验证模型的可行性。参照式(8),对基于地固坐标系的GNSS速度信息进行类似的坐标变换,即可将GNSS提供的速度信息融入到系统滤波模型中,进而提高组合导航系统的精度。
| [1] |
朱海微. 空天飞行器SINS/CNS/GNSS自主导航技术研究[D]. 南京: 南京航空航天大学, 2017 (Zhu Haiwei. Technologies for Autonomy SINS/CNS/GNSS Integrated Navigation System of Aerospace Vehicle[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017)
(  0) 0) |
| [2] |
孟阳, 高社生, 高兵兵, 等. 基于UKF的INS/GNSS/CNS组合导航最优数据融合方法[J]. 中国惯性技术学报, 2016, 24(6): 746-751 (Meng Yang, Gao Shesheng, Gao Bingbing, et al. UKF-Based Optimal Data Fusion Method for Integrated INS/GNSS/CNS[J]. Journal of Chinese Inertial Technology, 2016, 24(6): 746-751)
(  0) 0) |
| [3] |
张闯, 赵修斌, 庞春雷, 等. SINS/GNSS/CNS组合导航自适应容错联邦滤波方法[J]. 控制理论与应用, 2019, 36(9): 1469-1476 (Zhang Chuang, Zhao Xiubin, Pang Chunlei, et al. Adaptive Fault Tolerance Federated Filter Method for SINS/GNSS/CNS Integrated Navigation[J]. Control Theory and Applications, 2019, 36(9): 1469-1476)
(  0) 0) |
| [4] |
Quan W, Fang J C, Xu F, et al. Hybrid Simulation System Study of SINS/CNS Integrated Navigation[J]. IEEE Aerospace and Electronic Systems Magazine, 2008, 23(2): 17-24 DOI:10.1109/MAES.2008.4460727
(  0) 0) |
| [5] |
郁丰, 熊智, 屈蔷. 基于多圆交汇的天文定位与组合导航方法[J]. 宇航学报, 2011, 32(1): 88-92 (Yu Feng, Xiong Zhi, Qu Qiang. Multiple Circle Intersection-Based Celestial Positioning and Integrated Navigation Algorithm[J]. Journal of Astronautics, 2011, 32(1): 88-92 DOI:10.3873/j.issn.1000-1328.2011.01.013)
(  0) 0) |
| [6] |
黄远, 王可东, 刘宝, 等. 机动天基平台惯性/天文组合导航的研究[J]. 系统仿真学报, 2010, 22(增): 47-49 (Huang Yuan, Wang Kedong, Liu Bao, et al. The Research on the Inertial/Celestial Integrated Navigation System of the Mobile Space-Based Platform[J]. Journal of System Simulation, 2010, 22(S): 47-49)
(  0) 0) |
| [7] |
邓红, 刘光斌, 陈昊明, 等. 发射惯性坐标系下误差角与数学平台失准角的推导与仿真[J]. 宇航学报, 2011, 32(4): 781-786 (Deng Hong, Liu Guangbin, Chen Haoming, et al. Deduction and Simulation of Angular Error Relationship in "SINS/CNS" Integrated Navigation System[J]. Journal of Astronautics, 2011, 32(4): 781-786 DOI:10.3873/j.issn.1000-1328.2011.04.012)
(  0) 0) |
| [8] |
林雪原, 孙玉梅, 董云云, 等. 多传感器组合导航系统的改进多尺度滤波算法[J]. 中国空间科学技术, 2020, 40(4): 61-68 (Lin Xueyuan, Sun Yumei, Dong Yunyun, et al. Improved Multi-Scale Filtering Algorithm of Multi-Sensor Integrated Navigation System[J]. Chinese Space Science and Technology, 2020, 40(4): 61-68)
(  0) 0) |
| [9] |
Hu H D, Huang X L. SINS/CNS/GPS Integrated Navigation Algorithm Based on UKF[J]. Journal of Systems Engineering and Electronics, 2010, 21(1): 102-109 DOI:10.3969/j.issn.1004-4132.2010.01.017
(  0) 0) |
| [10] |
Levine S, Dennis R, Bachman K L. Strapdown Astro-Inertial Navigation Utilizing the Optical Wide-Angle Lens Startracker[J]. Navigation, 1990, 37(4): 347-362
(  0) 0) |
| [11] |
全伟, 刘百奇, 宫晓琳, 等. 惯性/天文/卫星组合导航技术[M]. 北京: 国防工业出版社, 2011 (Quan Wei, Liu Baiqi, Gong Xiaolin, et al. INS/CNS/GNSS Integrated Navigation Technology[M]. Beijing: National Defense Industry Press, 2011)
(  0) 0) |
| [12] |
潘加亮, 熊智, 王丽娜, 等. 一种简化的发射系下SINS/GPS/CNS组合导航系统无迹卡尔曼滤波算法[J]. 兵工学报, 2015, 36(3): 484-491 (Pan Jialiang, Xiong Zhi, Wang Lina, et al. A Simplified UKF Algorithm for SINS/GPS/CNS Integrated Navigation System in Launch Inertial Coordinate System[J]. Acta Armamentarii, 2015, 36(3): 484-491 DOI:10.3969/j.issn.1000-1093.2015.03.016)
(  0) 0) |
| [13] |
林雪原, 李荣冰, 高青伟. 组合导航及其信息融合方法[M]. 北京: 国防工业出版社, 2017 (Lin Xueyuan, Li Rongbing, Gao Qingwei. Integrated Navigation and Its Information Fusion Method[M]. Beijing: National Defense Industry Press, 2017)
(  0) 0) |
| [14] |
袁信, 俞济祥, 陈哲. 导航系统[M]. 北京: 航空工业出版社, 1993 (Yuan Xin, Yu Jixiang, Chen Zhe. Navigation System[M]. Beijing: Aviation Industry Press, 1993)
(  0) 0) |
2. College of Astronautics, Nanjing University of Aeronautics and Astronautics, 29 Yudao Street, Nanjing 210016, China;
3. School of Chemistry and Chemical Engineering, Beijing Institute of Technology, 5 South-Zhongguancun Street, Beijing 100081, China
 2021, Vol. 41
2021, Vol. 41


