2. 山东科技大学测绘与空间信息学院,青岛市前湾港路579号,266590
高精度的卫星钟差预报对于满足动态精密单点定位需求具有重要意义[1-5]。由于星载原子钟时频特性复杂且极易受外界环境影响,卫星钟差通常表现出显著的周期变化与随机特性,使得已有的钟差预报模型在应用中存在一定局限性。常用的钟差预报模型有二次多项式模型、灰色预报模型、卡尔曼滤波模型、自回归模型、自回归滑动平均模型和支持向量机模型[5-8]。于烨等[4]利用最小一乘法改进灰色系统钟差预报模型,结果表明该算法适用于GPS卫星钟差波动较大的情况,但算法的精度仍然相对较低。李成龙等[5]利用改进的粒子群算法优化灰色系统模型,并将该模型应用于GPS卫星钟差预报,结果表明该钟差模型精度高、稳定性好,但并未对BDS卫星钟差预报展开相应研究。李源等[9]利用粒子群算法优化分数阶灰色系统钟差预报模型,结果表明该算法精度高于传统二次多项式模型和灰色系统模型,但算法结构复杂,且未对BDS卫星钟差预报进行研究。
随着我国BDS-3卫星系统组网成功,建立高精度的BDS卫星钟差预报模型具有重要意义。本文将改进的萤火虫算法与分数阶离散型灰色系统模型相结合,实现分数阶最优阶数的选取,并将该模型应用于BDS卫星钟差预报。利用iGMAS提供的实测钟差数据进行实验分析,结果表明该模型精度优于二次多项式模型、DGM(1, 1)模型和GM(1, 1)模型。
1 分数阶离散型灰色系统模型FDGM (1, 1)为解决离散型灰色系统模型DGM(1, 1)扰动界大的问题,吴利丰等[10]提出分数阶离散型灰色系统模型。设观测值序列为X(0)={X(0)(1), X(0)(2), …, X(0)(n)},其r(0<r<1)阶累加序列为X(r)={X(r)(1), X(r)(2), …, X(r)(n)}(其中
| $ {\hat x^{(r)}}(k + 1) = {\beta _1}{\hat x^{(r)}}(k) + {\beta _2} $ | (1) |
式中,k=1, 2, 3, …, n-1;β1、β2为待估参数。
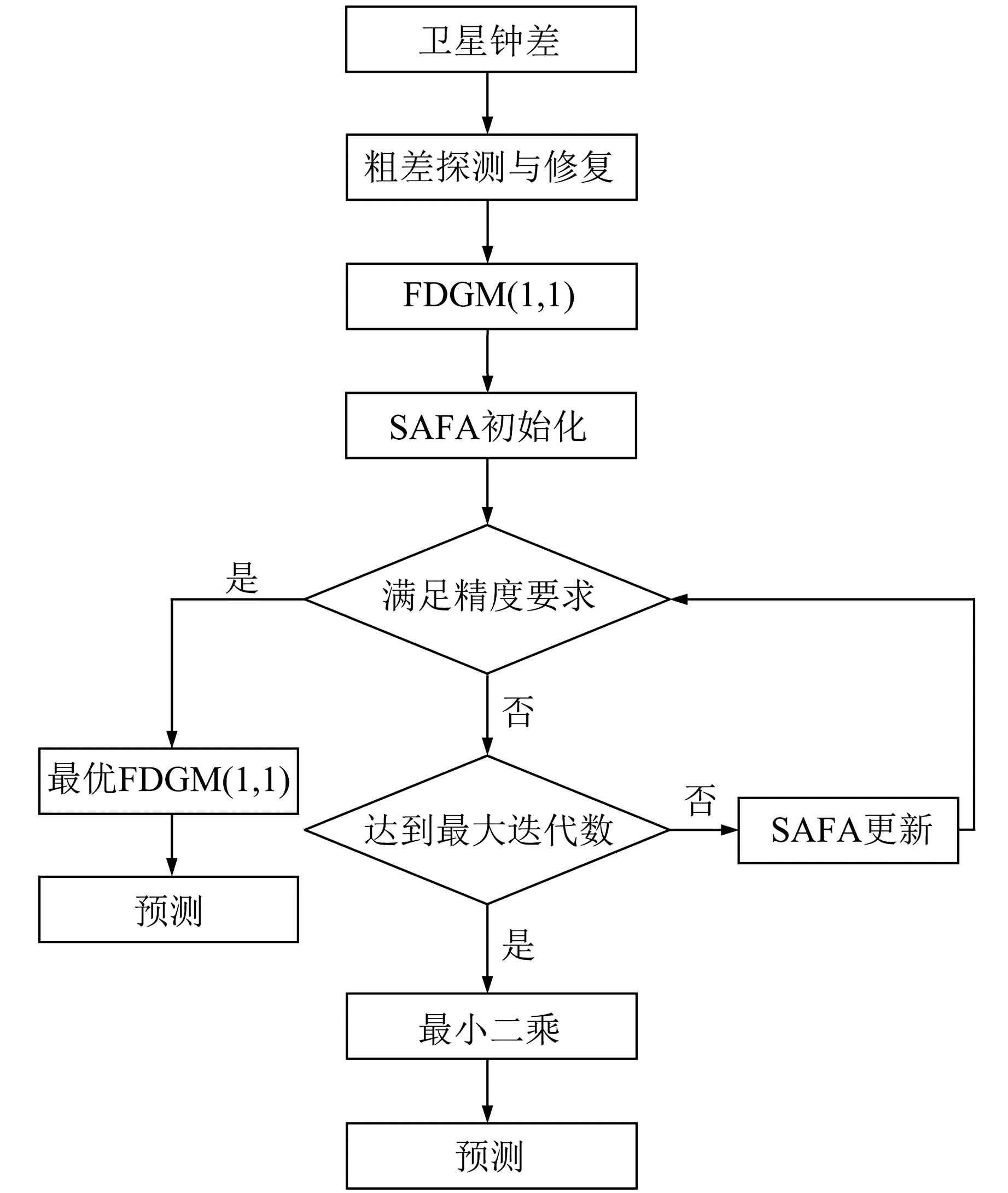
2 SAFA-FDGM(1, 1)模型针对分数阶离散型灰色系统模型阶数无法自动优化选取的问题,本文提出利用改进的萤火虫算法(SAFA)优化分数阶离散型灰色系统,建立SAFA-FDGM(1, 1)模型(图 1)。
|
图 1 基于SAFA-FDGM(1, 1)的钟差预报流程 Fig. 1 Flow chart of clock error prediction based on SAFA-FDGM(1, 1) |
为提高萤火虫算法[11-13]的优化能力,本文将粒子群算法中自适应惯性权重因子[14]引入到萤火虫算法中,并利用分群思想对惯性权重因子进行更新,即
| $ {w_i}(t) = \left\{ {\begin{array}{*{20}{l}} {0.9 - 0.5 \times \frac{1}{{1 + {{\rm{e}}^{3.4 - 0.07t}}}}, {I_i} > {I_{{\rm{avg}}}}}\\ {0.9, {I_i} \le {I_{{\rm{avg}}}}} \end{array}} \right. $ | (2) |
式中,t为当前迭代次数,Iavg为萤火虫种群平均亮度,Ii为个体i亮度。
改进后的算法位置更新公式为:
| $ \begin{array}{l} {x_i}(t + 1) = {\rm{ }}{w_i}(t){x_i}(t) + \beta ({x_j}(t) - \\ \;\;\;\;\;\;\;{x_i}(t)) + \alpha ({\rm{rand}} - 0.5) \end{array} $ | (3) |
在迭代初期,对于亮度较小的个体通过增加其惯性权重来加强全局搜索能力,对于亮度较大的个体通过降低其惯性权重来加强局部搜索能力;在迭代后期,对于亮度仍然较小的个体通过保持其惯性权重较大使其收敛于全局最优解,对于亮度较大的个体则保持其惯性权重较小来进一步提高其局部搜索能力。为了进一步提高算法的优化能力,步长因子采用文献[13]方法进行更新。
2.2 仿真实验分析为验证改进的萤火虫算法的优化能力,本文利用4个测试函数进行最小寻优实验。由表 1可知,改进的萤火虫算法(SAFA)寻优精度高,不易陷入局部最优解,相比于基本萤火虫算法(FA),其全局寻优能力得到显著提升。
|
|
表 1 各算法30次寻优结果的均方根误差 Tab. 1 The root mean square error of 30 optimization results of each algorithm |
1) 对BDS钟差数据进行预处理,去除粗差数据,并通过插值算法修复其异常值。
2) 设BDS原始观测钟差序列为X(0)={X(0)(1), X(0)(2), …, X(0)(n)},通过历元差分降低BDS钟差数据的数量级,提高模型预报精度,即
| $ \Delta {X^{(0)}} = \left\{ {\Delta {X^{(0)}}(1), \Delta {X^{(0)}}(2), \cdots , \Delta {X^{(0)}}(n - 1)} \right\} $ | (4) |
式中,ΔX(0)(k)=X(0)(k+1)-X(0)(k),k=1, 2, 3, …, n-1。
3) 基于差分拟合数据均方根误差最小准则,将分数阶离散型灰色系统模型的阶数作为萤火虫个体,利用SAFA算法优化获取分数阶离散型灰色系统模型(FDGM(1, 1))的最优阶数r。
4) 根据最优阶数r确定FDGM(1, 1)模型结构,进行BDS钟差预报。
3 实验分析 3.1 数据来源为验证算法的有效性和可行性,本文利用iGMAS提供的2018-10-05的BDS精密钟差数据进行BDS钟差预报,数据采样间隔为5 min。针对不同BDS卫星轨道,分别选用C02(GEO)、C09(IGSO)、C12(MEO)卫星进行实验分析。
3.2 建模方案采用前10 h的钟差数据作为样本数据分别建立SAFA-FDGM(1, 1)模型、二次多项式模型、GM(1, 1)模型,利用各模型进行BDS 3 h、6 h、9 h、12 h钟差预报实验。由于BDS精密钟差数据的精度优于0.5 ns,故可将其作为真值。将BDS钟差数据拟合残差的绝对值最大值、最小值、均方根误差作为实验精度评价指标。
3.3 结果分析从表 2~5可以看出,对于GEO卫星,SAFA-FDGM(1, 1)模型预报精度最高,3~6 h最大预报误差优于1 ns,3~12 h预报均方根误差优于1 ns;二次多项式模型预报精度次之;GM(1, 1)模型预报精度最差,其最大预报偏差高达100 ns量级。对于IGSO卫星,SAFA-FDGM(1, 1)模型预报精度最高,3~6 h最大预报误差小于1 ns,9~12 h最大预报误差优于2 ns;二次多项式模型次之;GM(1, 1)模型预报误差最大,其最大预报偏差达10 ns量级。对于MEO卫星,3种模型12 h内预报精度均较高,均方根误差均优于4 ns,其中SAFA-FDGM(1, 1)模型预报精度最高,12 h内预报均方根误差优于1 ns;GM(1, 1)模型次之,其12 h内预报均方根误差优于3 ns;二次多项式模型预报精度最低,其12 h内预报均方根误差优于4 ns。
|
|
表 2 各模型3 h预报精度评估 Tab. 2 Evaluation of 3 h forecast accuracy of each model |
|
|
表 3 各模型6 h预报精度评估 Tab. 3 Evaluation of 6 h forecast accuracy of each model |
|
|
表 4 各模型9 h预报精度评估 Tab. 4 Evaluation of 9 h forecast accuracy of each model |
|
|
表 5 各模型12 h预报精度评估 Tab. 5 Evaluation of 12 h forecast accuracy of each model |
由实验可知,SAFA-FDGM(1, 1)模型对不同类型北斗卫星钟差预测的精度存在差异,这主要是由于在卫星定轨和钟差求解过程中不同类型北斗卫星的解算策略不同。
4 结语为建立BDS通用的钟差预报模型,针对BDS卫星钟差特点,本文提出一种基于SAFA-FDGM(1, 1) 模型的BDS钟差预报模型。实验结果表明,该模型在3~12 h内预报精度优于1 ns,最大预报误差小于2 ns,优于传统二次多项式模型和GM(1, 1) 模型,对建立高精度的BDS钟差预报模型具有重要参考价值。
| [1] |
于烨, 张慧君, 李孝辉, 等. 基于Vondrák滤波1阶差分灰色模型的卫星钟差预报方法[J]. 天文学报, 2018, 59(2): 73-82 (Yu Ye, Zhang Huijun, Li Xiaohui, et al. Prediction Method of Satellite Clock Bias Based on Grey Model of First-Order Difference of Vondrák Filter[J]. Acta Astronomica Sinica, 2018, 59(2): 73-82)
(  0) 0) |
| [2] |
宫晓春, 王宇谱, 王宁, 等. GPS卫星钟差改正数实时预报算法[J]. 武汉大学学报: 信息科学版, 2018, 43(6): 867-873 (Gong Xiaochun, Wang Yupu, Wang Ning, et al. Real-Time Prediction of GPS Satellite Clock Bias Correction[J]. Geomatics and Information Science of Wuhan University, 2018, 43(6): 867-873)
(  0) 0) |
| [3] |
王宇谱, 陈正生, 李伟杰, 等. BDS卫星钟差短期预报性能分析[J]. 大地测量与地球动力学, 2017, 37(5): 450-456 (Wang Yupu, Chen Zhengsheng, Li Weijie, et al. Analyzing the Short-Term Prediction Performance of BDS Satellite Clock Bias[J]. Journal of Geodesy and Geodynamics, 2017, 37(5): 450-456)
(  0) 0) |
| [4] |
于烨, 黄默, 王小青, 等. 利用最小一乘法改进的灰色模型的导航卫星钟差预报[J]. 测绘通报, 2019(4): 1-6 (Yu Ye, Huang Mo, Wang Xiaoqing, et al. Navigation Satellite Clock Bias Prediction Based on Grey Model Improved by Least Absolute Deviations[J]. Bulletin of Surveying and Mapping, 2019(4): 1-6)
(  0) 0) |
| [5] |
李成龙, 陈西宏, 刘继业, 等. 利用自适应TS-IPSO优化的灰色系统预报卫星钟差[J]. 武汉大学学报: 信息科学版, 2018, 43(6): 854-859 (Li Chenglong, Chen Xihong, Liu Jiye, et al. Predicting Satellite Clock Errors Using Grey Model Optimized by Adaptive TS-IPSO[J]. Geomatics and Information Science of Wuhan University, 2018, 43(6): 854-859)
(  0) 0) |
| [6] |
雷雨, 赵丹宁, 蔡宏兵. 利用结构自适应极端学习机预报导航卫星钟差[J]. 武汉大学学报: 信息科学版, 2018, 43(5): 664-668 (Lei Yu, Zhao Danning, Cai Hongbing. Prediction of Navigation Satellite Clock Offset by Adaptive Extreme Learning Machine[J]. Geomatics and Information Science of Wuhan University, 2018, 43(5): 664-668)
(  0) 0) |
| [7] |
陈演羽, 李廷会, 黄飞江, 等. 基于混沌时间序列的GPS卫星钟差预测算法[J]. 仪器仪表学报, 2018, 39(4): 115-122 (Chen Yanyu, Li Tinghui, Huang Feijiang, et al. GPS Satellite Clock Bias Prediction Algorithm Based on Chaotic Time Series[J]. Chinese Journal of Scientific Instrument, 2018, 39(4): 115-122)
(  0) 0) |
| [8] |
王利, 张勤, 黄观文, 等. 基于指数平滑法的GPS卫星钟差预报[J]. 武汉大学学报: 信息科学版, 2017, 42(7): 995-1001 (Wang Li, Zhang Qin, Huang Guanwen, et al. GPS Satellite Clock Bias Prediction Based on Exponential Smoothing Method[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 995-1001)
(  0) 0) |
| [9] |
李源, 战兴群, 梅浩, 等. 灰色粒子群自适应卫星钟差预报方法[J]. 哈尔滨工业大学学报, 2018, 50(4): 71-77 (Li Yuan, Zhan Xingqun, Mei Hao, et al. Particle Swarm Adaptive Satellite Clock Error Prediction Model Based on Grey Theory[J]. Journal of Harbin Institute of Technology, 2018, 50(4): 71-77)
(  0) 0) |
| [10] |
吴利丰, 刘思峰, 姚立根. 基于分数阶累加的离散灰色模型[J]. 系统工程理论与实践, 2014, 34(7): 1822-1827 (Wu Lifeng, Liu Sifeng, Yao Ligen. Discrete Grey Model Based on Fractional Order Accumulate[J]. Systems Engineering——Theory and Practice, 2014, 34(7): 1822-1827)
(  0) 0) |
| [11] |
Yang X S. Nature-Inspired Metaheuristic Algorithms[M]. London: Luniver Press, 2008
(  0) 0) |
| [12] |
Yang X S. Firefly Algorithms for Multimodal Optimization[C]. Proceedings of the 5th International Conference on Stochastic Algorithms: Foundations and Applications, Heidelberg, 2009
(  0) 0) |
| [13] |
汪靖, 刘桂元. 基于动态步长变化的萤火虫算法[J]. 计算机工程与设计, 2019, 40(4): 1001-1007 (Wang Jing, Liu Guiyuan. Improved Firefly Algorithm Based on Dynamic Step[J]. Computer Engineering and Design, 2019, 40(4): 1001-1007)
(  0) 0) |
| [14] |
黄洋, 鲁海燕, 许凯波, 等. 基于S型函数的自适应粒子群优化算法[J]. 计算机科学, 2019, 46(1): 245-250 (Huang Yang, Lu Haiyan, Xu Kaibo, et al. S-Shaped Function Based Adaptive Particle Swarm Optimization Algorithm[J]. Computer Science, 2019, 46(1): 245-250)
(  0) 0) |
2. College of Geodesy and Geomatics, Shandong University of Science and Technology, 579 Qianwangang Road, Qingdao 266590, China
 2021, Vol. 41
2021, Vol. 41

