2. 华东交通大学土木建筑学院,南昌市双港东大街808号,330013
电离层不仅与无线电通讯、广播、卫星导航、雷达定位等人类日常活动密切相关,还对地震形成研究与地震前期预报具有重要意义[1]。电离层总电子含量(total electric content, TEC)是电离层物理参量之一,建立高精度的电离层TEC预报模型对电离层理论研究和电离层电波传播应用研究具有重要意义[2]。在常用的线性模型预报方法中,时间序列分析因模型简单、预报精度较高而被广泛应用[3-4],陈鹏等[3]利用时间序列分析对电离层TEC进行预报,预报7 d残差结果中95.3%小于±3 TECu。在非线性模型预报方法中,神经网络模型应用广泛,李淑慧等[5]利用神经网络预报提前1 d的电离层TEC值,预报结果可反映不同季节TEC的日变化特征。灰色模型在部分数据预测中表现较好,预测单调变化的时间序列时精度较高。Shi等[6]将灰色模型应用到TEC点对点的短期预报中,并用残差修正进行补偿细化,结果表明改进后的预报模型更加准确。
电离层复杂的空间分布及时间变化使电离层TEC时间序列具有非线性、非平稳的特点,因此采用单一的预报方法缺乏对TEC数据变化规律的把握,难以从本质上获得较高的预测精度,往往会在电离层剧烈变化的预测点产生较大的误差[4]。近年来,经验模态分解(empirical mode decomposition, EMD)和小波分析结合时间序列以及神经网络的各种组合在电离层预测方面取得广泛应用[7-8],汤俊等[7]将EMD应用到电离层TEC预测当中,结果表明组合模型比单一模型的预报效果更优。但EMD缺乏严格的理论支撑,且容易出现模态混叠现象,不仅会影响分量分解的准确性,还会增加累积误差和工作量[9]。经验小波变换(empirical wavelet transform, EWT)以小波分析为理论框架对数据进行分解,其比EMD方法更具理论性和鲁棒性[10]。Elman神经网络作为具有局部记忆单元和局部反馈连接的神经网络,其比BP神经网络具有更强的动态信息处理能力。基于此,本文建立EWT和Elman神经网络的短期电离层组合预报模型,并将预报结果与IGS中心的真实值进行对比分析。
1 算法原理 1.1 经验小波变换基本原理EWT是以小波分析为理论框架而建立的自适应信号分解方法[10],其核心思想是根据信号本身的频谱特征建立一组经验小波滤波器组,用以提取信号的不同模态,具体过程可参考文献[11]。
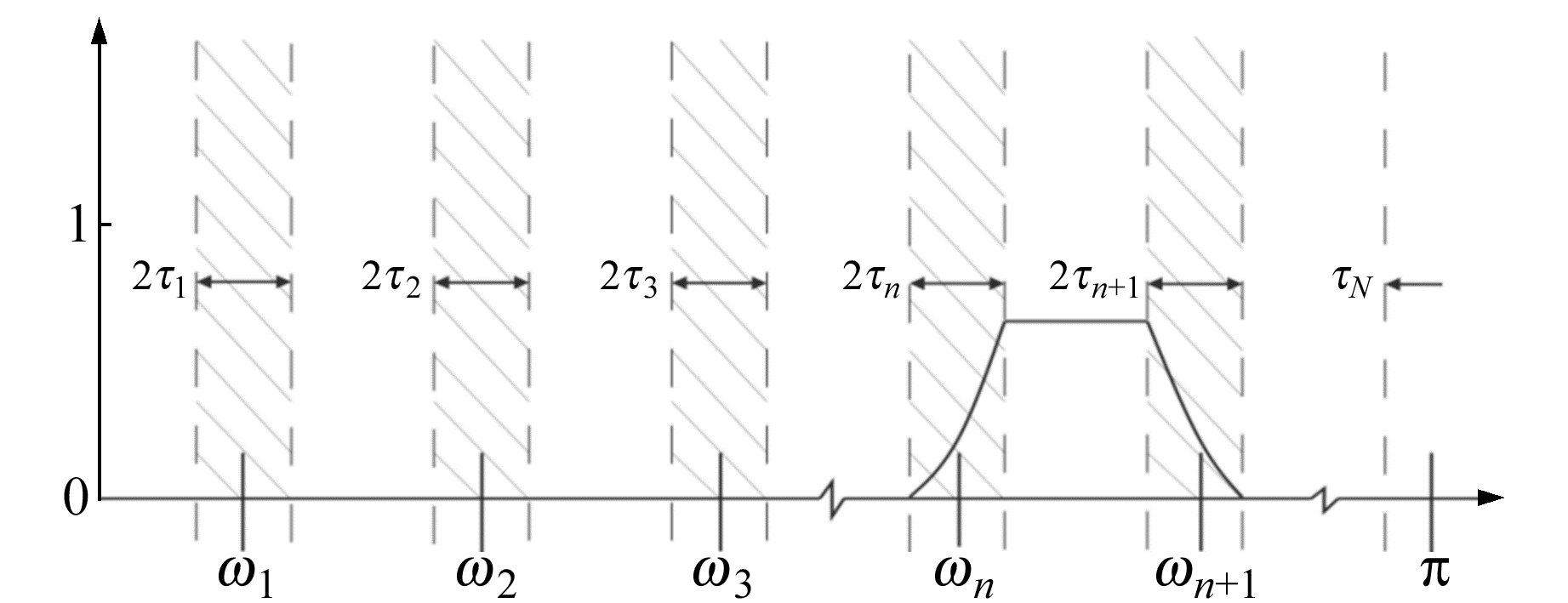
图 1为根据频谱划分构造经验小波示意图,其中ωn为相邻频带之间的边界,ω0=0, ωN=π。以ωn为中心可定义宽度Tn=2τn的过渡带,如图中阴影部分所示。各频带根据边界可表示为Λn=[ωn-1, ωn],∪n=1N=[0, π]。经验小波由经验尺度函数和经验小波函数构成,可分别用式(1)和式(2)表示[10]:
| $ {\hat \phi _n}(\omega ) = \left\{ {\begin{array}{*{20}{l}} {1, |\omega | \le {\omega _n} - {\tau _n}}\\ {\cos \left\{ {\frac{\pi }{2}\beta \left[ {\frac{1}{{2{\tau _n}}}\left( {|\omega | - {\omega _n} + {\tau _n}} \right)} \right]} \right\}, }\\ {\;\;\;{\omega _n} - {\tau _n} \le |\omega | \le {\omega _n} + {\tau _n}}\\ {0, 其他} \end{array}} \right. $ | (1) |
| $ {\hat \Psi _n}(\omega ) = \left\{ {\begin{array}{*{20}{l}} {1, {\omega _n} + {\tau _n} \le |\omega | \le {\omega _{n + 1}} - {\tau _{n + 1}}}\\ {\cos \left\{ {\frac{\pi }{2}\beta \left[ {\frac{1}{{2{\tau _{n + 1}}}}\left( {|\omega | - {\omega _{n + 1}} + {\tau _{n + 1}}} \right)} \right]} \right\}, }\\ {\quad {\omega _{n + 1}} - {\tau _{n + 1}} \le |\omega | \le {\omega _{n + 1}} + {\tau _{n + 1}}}\\ {\sin \left\{ {\frac{\pi }{2}\beta \left[ {\frac{1}{{2{\tau _n}}}\left( {|\omega | - {\omega _n} + {\tau _n}} \right)} \right]} \right\}, }\\ {\quad {\omega _n} - {\tau _n} \le |\omega | \le {\omega _n} + {\tau _n}}\\ {0, 其他} \end{array}} \right. $ | (2) |
|
图 1 傅里叶频谱划分 Fig. 1 Fourier spectrum division |
式中,τn和β(x)可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _n} = \gamma {\omega _n}, 0 < \gamma < 1 且 \gamma < \min \left\{ {\frac{{{\omega _{n + 1}} - {\omega _n}}}{{{\omega _{n + 1}} + {\omega _n}}}} \right\}}\\ {\beta (x) = {x^4}\left( {35 - 84x + 70{x^2} - 20{x^3}} \right)} \end{array}} \right. $ | (3) |
重构的原始信号可表示为:
| $ f(t) = W_f^\varepsilon (0, t)*{\phi _1}(t) + \sum\limits_{n = 1}^N {W_f^\varepsilon } (n, t)*{\psi _n}(t) $ | (4) |
式中,*为卷积运算,Wfε(0, t)为傅里叶变换后的近似系数,Wfε(n, t)为傅里叶变换后的细节系数。
1.2 Elman神经网络原理Elman神经网络是一种典型的局部回归神经网络[12],其在BP神经网络结构的基础上,在隐含层中增加1个承接层,每个隐含层的神经元均有对应的承接层神经元与之相连。Elman神经网络一般由输入层、中间层(隐含层)、承接层和输出层4部分组成,其中输入层、隐含层和输出层与其他前馈神经网络的作用相似,即信号从输入层神经元进入网络,通过隐含层的加权作用到达输出层,经过非线性变换输出信号;承接层又称状态层,其作用是记忆隐含层前一时刻的输出。隐含层的输出通过输入层加权处理后,在承接层中进行延时和存储,然后到达输出层。这种连接方式会增加网络结构对历史数据的敏感性,增强网络自身处理动态信息的能力,从而可动态建模。
Elman神经网络的数学表达式为:
| $ x(k) = f\left( {{\omega _1}(u(k - 1)) + {\omega _2}{x_c}(k)} \right) $ | (5) |
| $ {x_c}(k) = x(k - 1) $ | (6) |
| $ y(k) = g\left( {{\omega _3}x(k)} \right) $ | (7) |
式中,ω1为输入层到隐含层的权值;ω2为承接层到隐含层的权值;ω3为隐含层到输出层的权值;u(k-1)为神经网络的输入;x(k)为隐含层的输出;xc(k)为承接层的输出;y(k)为神经网络的输出。g为输出层传递函数,为隐含层输出的线性组合;f为隐含层传递函数,一般为Sigmoid函数,表达式为:
| $ f(x) = {(1 + {e^{ - x}})^{ - 1}} $ | (8) |
Elman神经网络采用传统算法修正权值,误差函数的表达式为:
| $ E = \mathop \sum \limits_{k = 1}^m {({t_k} - {y_k})^2} $ | (9) |
式中,tk为期望输出。
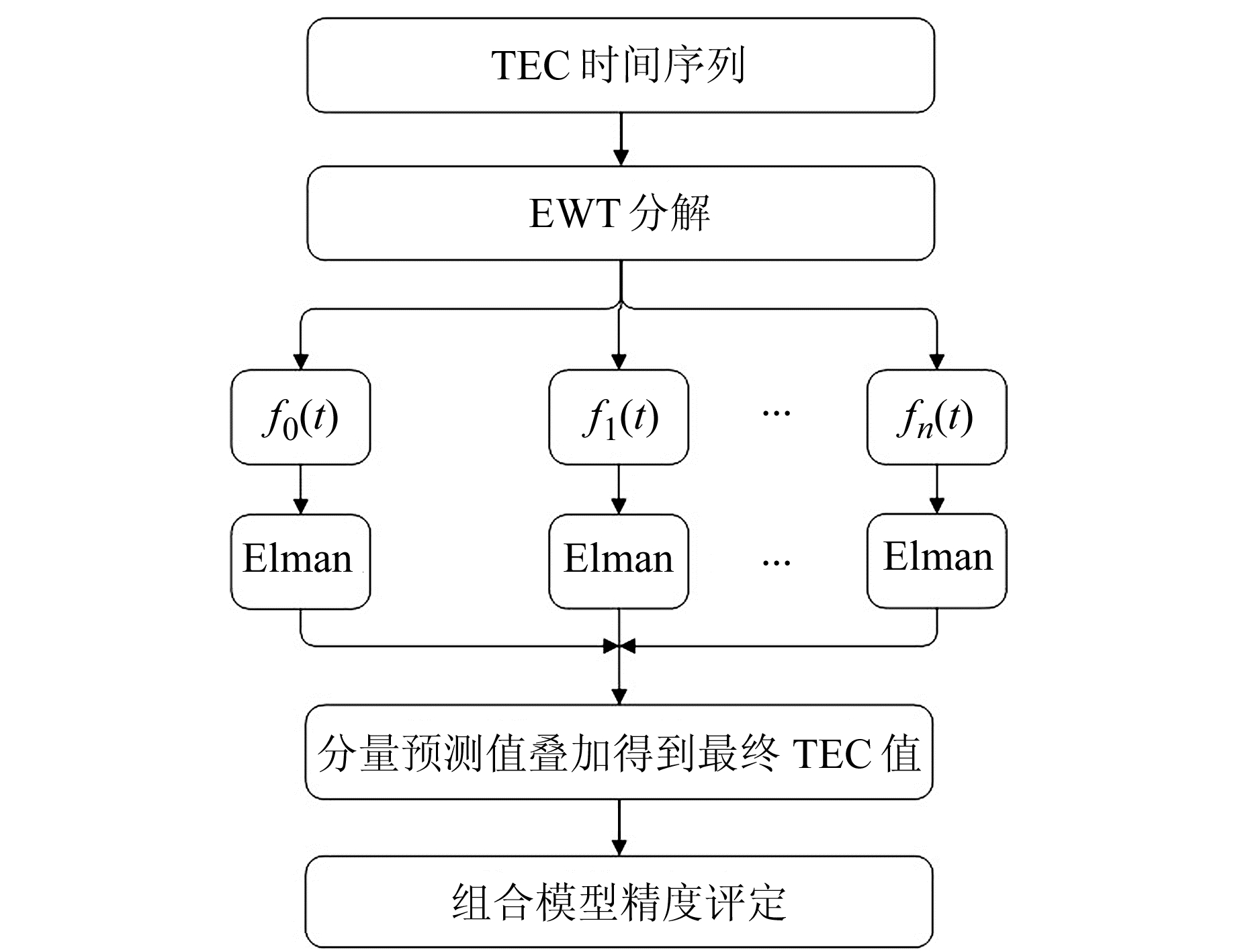
1.3 组合模型原理图 2为EWT-Elman组合模型算法流程图。
|
图 2 EWT-Elman组合模型流程 Fig. 2 Flow chart of EWT-Elman combination model |
本文结合EWT理论性强、分解模态分量少以及Elman稳定性强、预测精度高的优点,建立EWT-Elman组合预测模型,具体步骤为:
1) 利用EWT对不同地磁环境的TEC时间序列x(t)进行分解,分别得到1个经验尺度分量和3~5个经验小波分量,可表示为:
| $ x(t) = {f_0}(t) + \mathop \sum \limits_{i = 1}^n {f_i}(t) $ | (10) |
式中,f0为经验尺度分量,fi为经验小波分量,n为经验小波分量个数。
2) 基于分解的分量建立Elman神经网络模型进行预测。以前25 d数据作为训练样本进行模型训练,其中前24 d数据作为网络输入,第25 d数据作为网络输出,进行Elman单步预测;将后5 d数据作为测试样本检验模型的预报精度。
3) 对2)中各分量的预测值进行叠加得到最终TEC值,与IGS发布的真实值进行对比,验证模型预测效果。
2 实验结果与分析地磁指数Dst通常可描述地磁活动水平,一般认为当Dst≤-30 nT时存在弱磁暴,Dst≤-50 nT时存在中等磁暴,Dst≤-100 nT时存在强磁暴[13]。本文采用国际服务中心IGS提供的最终GIMs产品进行实验,根据地磁活动水平,选取2010年年积日第51~80 d(时段1)和第241~270 d(时段2)高纬度(75°N, 125°E)、中纬度(45°N, 125°E; 45°N, 60°W)和低纬度(15°N, 125°E)的电离层TEC数据作为地磁平静期数据;选取2014年年积日第31~60 d(时段3)、第101~130 d(时段4)和第211~240 d(时段5)高纬度(75°N, 125°E)、中纬度(45°N, 125°E; 45°N, 60°W) 和低纬度(15°N, 125°E)的电离层TEC数据作为地磁扰动期数据。以每个时段前25 d数据作为训练数据,后5 d数据作为测试数据检验模型的预报精度。
为验证EWT-Elman模型的预报精度,采用单一Elman模型、EMD-Elman模型和EWT-BP模型进行对比分析,以日平均相对精度RA和均方根误差RMSE作为预报效果的评价指标,其表达式为:
| $ {\rm{RA}} = 1 - \left| {{I_{{\rm{pre}}, i}} - {I_{{\rm{IGS}}, i}}} \right|/{I_{{\rm{IGS}}, i}} $ | (11) |
| $ {\rm{RMSE}} = \sqrt {\frac{1}{t}\mathop \sum \limits_{i = 1}^t {{\left( {{I_{{\rm{IGS}}, i}} - {I_{{\rm{pre}}, i}}} \right)}^2}} $ | (12) |
式中,Ipre, i为第i个历元的TEC预测值,IIGS, i为第i个历元的TEC实际值,t为预报的历元长度。
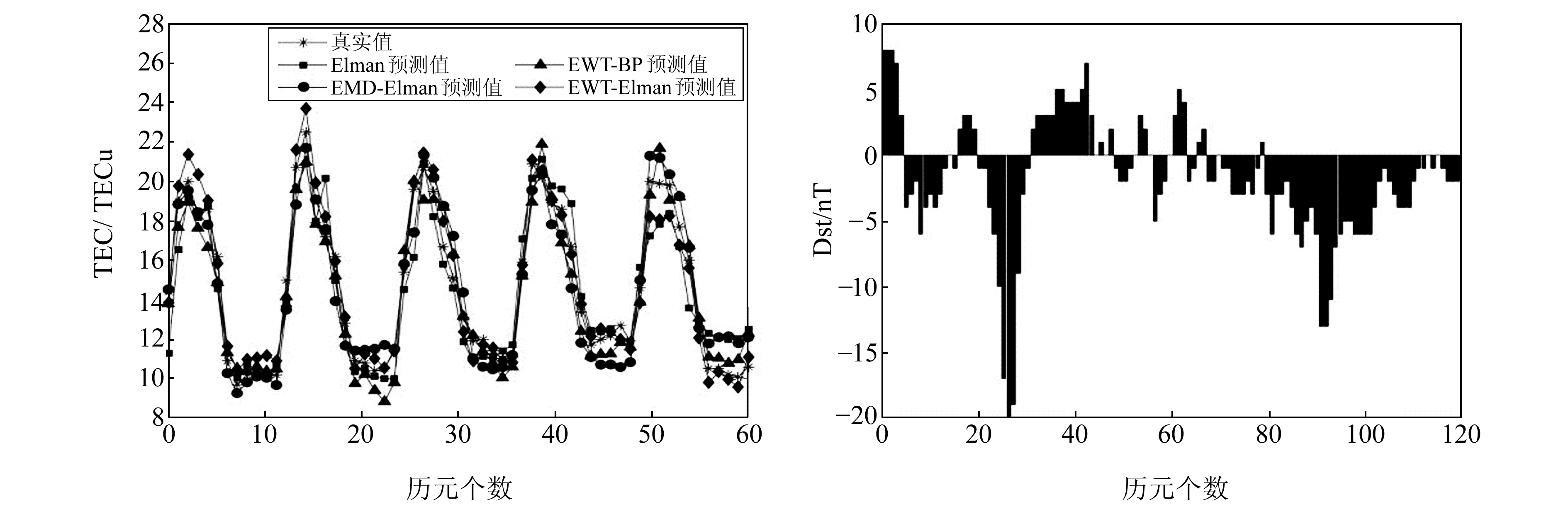
2.1 地磁平静期实验结果分析图 3为地磁平静期(时段1)不同模型TEC预报结果和地磁Dst指数图。TEC结果图横坐标为历元个数,以时长2 h为1个历元,纵坐标为电离层TEC值,单位为TECu,1 TECu=1016 e/m2;Dst指数图横坐标为历元个数,以时长1 h为1个历元,纵坐标为Dst值,单位为nT。从图中可以看出,Dst数值变化范围为-20~10 nT,虽然存在个别峰值变化,但未出现磁暴现象。与其他预报模型对比可知,EWT-Elman组合模型预报的TEC值整体上与真实TEC值更接近,表明预测效果更好。
|
图 3 时段1不同模型预报结果和地磁Dst指数 Fig. 3 Prediction results of different models and geomagnetic Dst index in period 1 |
表 1为地磁平静期4种模型不同时段残差的分布情况,从表中可以看出,单一Elman模型预报结果的平均残差中51.5%小于1 TECu,6.7%大于3 TECu;EMD-Elman组合模型预报结果的平均残差中51.7%小于1 TECu,3.1%大于3 TECu;EWT-BP组合模型预报结果的平均残差中50.9%小于1 TECu,3.1%大于3 TECu;而EWT-Elman组合模型预报结果的平均残差中67.3%小于1 TECu,1.7%大于3 TECu。整体结果表明,4种预测模型在地磁平静期均能有效预测电离层TEC值,而相比于其他预报模型,EWT-Elman组合模型的预测效果最优,与图 4呈现的结果一致。
|
|
表 1 地磁平静期不同时段的残差绝对值百分比统计 Tab. 1 Percentage statistics of absolute residual value in different periods during geomagnetic quiescence |
|
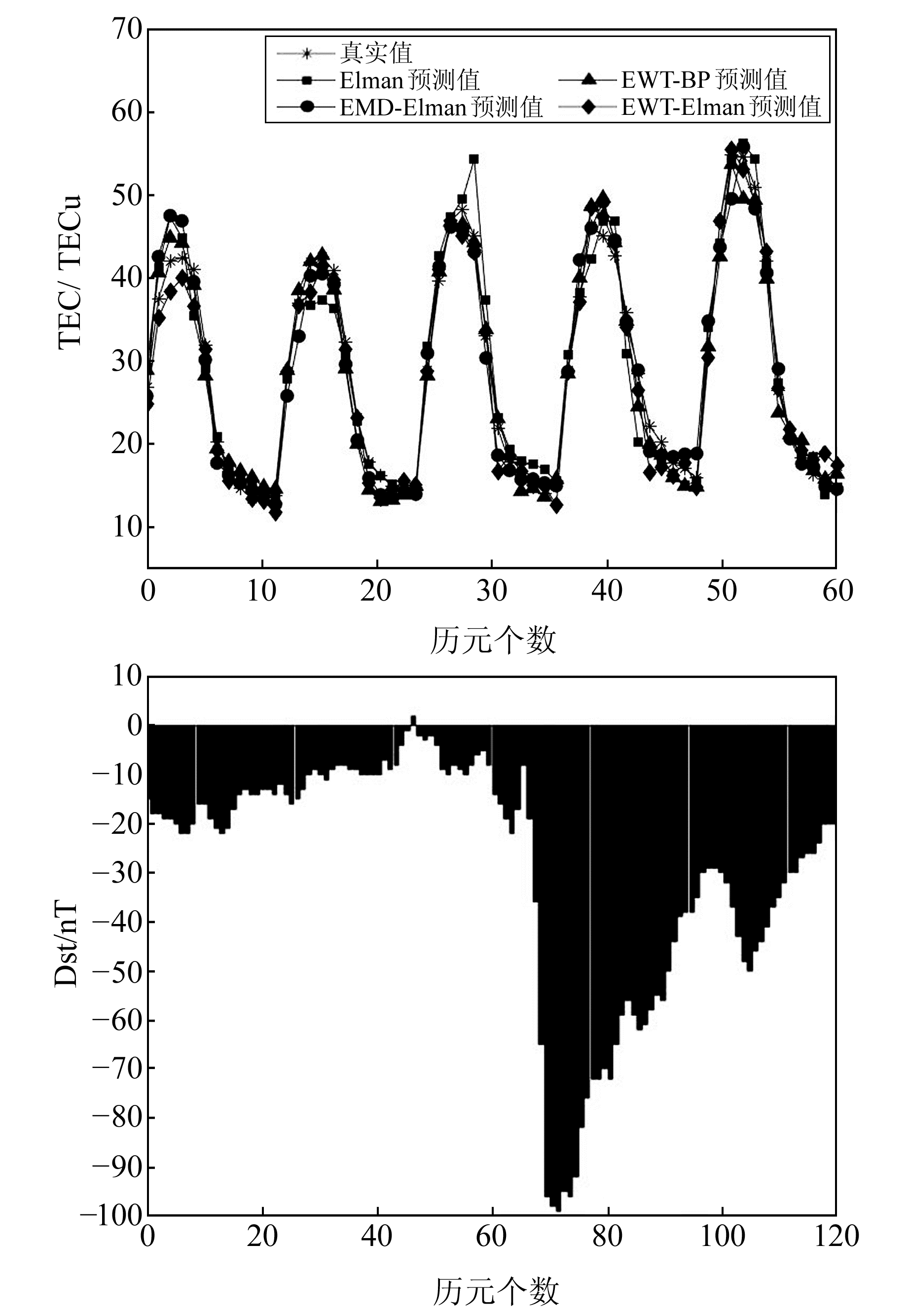
图 4 时段3不同模型预报结果和地磁Dst指数 Fig. 4 Prediction results of different models and geomagnetic Dst index in period 3 |
表 2为地磁平静期4种模型在不同地理位置的平均预测误差结果,从表中可以看出,在同一地理位置,EWT-Elman组合模型的预报效果优于其他预报模型,平均相对精度更高,且均方根误差更小,与表 1结果一致。在同一经度,预报均方根误差随纬度的增加而减小,相对精度无明显变化特征,主要由TEC含量和变化特征在不同纬度存在差异所造成。
|
|
表 2 地磁平静期不同地理位置的预测精度 Tab. 2 Prediction accuracy in different geographical locations during geomagnetic quiescence |
图 4为地磁扰动期(时段3)不同模型TEC预报结果和地磁Dst指数图,从图中可以看出,Dst指数变化范围为-100~10 nT,存在中等磁暴现象。在地磁扰动期,4种模型均能描述电离层TEC的变化特征,而EWT-Elman组合模型预测的TEC值整体上与真实TEC值更为接近。与地磁平静期相比,地磁扰动期TEC含量较高,波动较大,易产生较大的TEC预报残差。
表 3为地磁扰动期4种模型不同时段残差的分布情况。由表可知,单一Elman模型预报结果的平均残差中68.3%小于3 TECu,EMD-Elman组合模型预报结果的平均残差中74.9%小于3 TECu,EWT-BP组合模型预报结果的平均残差中76%小于3 TECu,而EWT-Elman组合模型预报结果的平均残差中81.8%小于3 TECu,表明本文组合模型的预测效果最优。但4种预测模型在地磁扰动期的残差小于3 TECu(IGS所给的精度范围)的占比较低,主要为太阳活动高年TEC含量和地磁扰动对TEC时空变化的影响所致。
|
|
表 3 地磁扰动期不同时段的残差绝对值百分比统计 Tab. 3 Percentage statistics of absolute residual value in different periods during geomagnetic disturbance |
表 4为地磁扰动期4种模型在不同地理位置的平均预报误差结果。由表可知,在同一地理位置,EWT-Elman组合模型的预报效果优于其他预报模型,平均相对精度更高,且均方根误差更小,与表 2地磁平静期的预测结果一致。低纬度地区4种模型预报结果的均方根误差均超过3 TECu,而中、高纬度地区的均方根误差均小于3 TECu。在同一经度,平均相对精度随纬度的增加而减小,主要由TEC含量和变化特征在不同纬度存在差异所致。
|
|
表 4 地磁扰动期不同地理位置的预测精度 Tab. 4 Prediction accuracy in different geographical locations of geomagnetic disturbance |
表 5为地磁平静期和扰动期不同时段整体预测效果对比。由表可知,在地磁平静期和扰动期,EWT-Elman组合模型的预测效果均最优。EWT-Elman组合模型在地磁平静期预报相对精度为93%,均方根误差为1.04 TECu;地磁扰动期预报相对精度为92.4%,均方根误差为2.18 TECu。结合表 1和表 3可知,本文组合模型在地磁平静期的预报效果优于地磁扰动期。
|
|
表 5 地磁平静期和扰动期不同时段整体预测效果对比 Tab. 5 Comparison of overall prediction results in different periods during geomagnetic quiescence and disturbance |
本文将经验小波变换应用到电离层数据处理中,结合Elman神经网络模型建立EWT-Elman组合预测模型,并与单一Elman模型、EMD-Elman组合模型和EWT-BP组合模型在相同环境下的预报效果进行对比,同时分析EWT-Elman组合模型在不同环境下(不同地磁环境和不同地理位置)的预报性能,得出以下结论:
1) 相比于单一Elman模型和EMD-Elman组合模型,EWT-Elman模型的预报效果更优,表明EWT在处理电离层数据时比EMD效果更好;与EWT-BP组合模型相比,EWT-Elman组合模型的预测性能更优,表明Elman预测比传统BP预测更加精确。
2) EWT-Elman模型能够反映电离层TEC的变化特征,地磁平静期模型预测的相对精度为93%,均方根误差为1.04 TECu;地磁扰动期模型预测的相对精度为92.4%,均方根误差为2.18 TECu。地磁扰动期的TEC含量以及不稳定性特征导致电离层在平静期的预测效果优于扰动期。
本文将EWT数据处理和Elman神经网络预测相结合,并将其应用于电离层TEC预报,预测效果较好,可为相似问题提供一种新的解决思路。但地磁活动等因素导致模型预测效果不佳以及在实际预报中部分时段预报效果较差的问题还有待进一步解决,需建立高精度、稳定性强的预测模型进行研究。
致谢: 感谢IGS中心提供电离层TEC数据。
| [1] |
张小红, 任晓东, 吴风波, 等. 震前电离层TEC异常探测新方法[J]. 地球物理学报, 2013, 56(2): 441-449 (Zhang Xiaohong, Ren Xiaodong, Wu Fengbo, et al. A New Method for Detection of Pre-Earthquake Ionospheric Anomalies[J]. Chinese Journal of Geophysics, 2013, 56(2): 441-449)
(  0) 0) |
| [2] |
Ren X D, Zhang X H, Xie W L, et al. Global Ionospheric Modelling Using Multi-GNSS: Beidou, Galileo, GLONASS and GPS[J]. Scientific Reports, 2016, 6(1): 33499 DOI:10.1038/srep33499
(  0) 0) |
| [3] |
陈鹏, 姚宜斌, 吴寒. 利用时间序列分析预报电离层TEC[J]. 武汉大学学报: 信息科学版, 2011, 36(3): 267-270 (Chen Peng, Yao Yibin, Wu Han. TEC Prediction of Ionosphere Based on Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 267-270)
(  0) 0) |
| [4] |
李磊, 张淑芳, 王轶卓, 等. 利用ARMA模型进行电离层TEC预报[J]. 应用基础与工程科学学报, 2013, 21(5): 814-822 (Li Lei, Zhang Shufang, Wang Yizhuo, et al. Ionospheric Total Electron Content Prediction Based on ARMA Model[J]. Journal of Basic Science and Engineering, 2013, 21(5): 814-822 DOI:10.3969/j.issn.1005-0930.2013.05.002)
(  0) 0) |
| [5] |
李淑慧, 彭军还, 徐伟超, 等. 利用神经网络预报短期电离层TEC变化[J]. 测绘科学, 2013, 38(1): 8-9 (Li Shuhui, Peng Junhuan, Xu Weichao, et al. Short-Term Ionospheric TEC Change Prediction by Neural Network[J]. Science of Surveying and Mapping, 2013, 38(1): 8-9)
(  0) 0) |
| [6] |
Shi H L, Lan G W. A Grey Model for Short-Term Prediction of the Ionospheric TEC[C]. International Conference on Geomatics in the Big Data Era(ICGBD), Guilin, 2019
(  0) 0) |
| [7] |
汤俊, 姚宜斌, 陈鹏, 等. 利用EMD方法改进电离层TEC预报模型[J]. 武汉大学学报: 信息科学版, 2013, 38(4): 408-411 (Tang Jun, Yao Yibin, Chen Peng, et al. Prediction Models of Ionospheric TEC Improved by EMD Method[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 408-411)
(  0) 0) |
| [8] |
吉长东, 王强, 沈祎凡, 等. 自回归神经网络的电离层总电子含量预报[J]. 导航定位学报, 2018, 6(4): 96-101 (Ji Changdong, Wang Qiang, Shen Yifan, et al. TEC Prediction of Ionospheric Based on Nonlinear Auto Regressive Model[J]. Journal of Navigation and Positioning, 2018, 6(4): 96-101)
(  0) 0) |
| [9] |
王新友, 李青, 郑少鹏. 基于EWT-ESN的短期风电功率预测研究[J]. 太阳能学报, 2018, 39(3): 633-642 (Wang Xinyou, Li Qing, Zheng Shaopeng. Short-Term Wind Power Prediction Based on EWT-ESN[J]. Acta Energiae Solaris Sinica, 2018, 39(3): 633-642)
(  0) 0) |
| [10] |
Gilles J. Empirical Wavelet Transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010
(  0) 0) |
| [11] |
王莹. 基于成分分解的自适应滤波降噪方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2017 (Wang Ying. Research on Adaptive Filter Denoising Method Based on Component Decomposition[D]. Harbin: Harbin Institute of Technology, 2017)
(  0) 0) |
| [12] |
Elman J L. Finding Structure in Time[J]. Cognitive Science, 1990, 14(2): 179-211
(  0) 0) |
| [13] |
Gonzalez W D, Joselyn J A, Kamide Y, et al. What is a Geomagnetic Storm?[J]. Journal of Geophysical Research: Space Physics, 1994, 99(A4): 5771-5792
(  0) 0) |
2. School of Civil Engineering and Architecture, East China Jiaotong University, 808 East-Shuanggang Street, Nanchang 330013, China
 2021, Vol. 41
2021, Vol. 41


