2. 地震预警湖北省重点实验室,武汉市洪山侧路48号,430071
地震背景噪声技术改变了传统的地球物理学研究对地震事件的依赖,被认为是地球物理学的重大突破。2007年,Bensen等[1]系统总结了由背景噪声数据提取面波频散曲线的处理方法,之后基于地震背景噪声的Rayleigh波和Love波层析成像技术在研究壳幔结构中得到广泛应用。虽然Koper等[2]对0.25~2.5 s周期的地震背景噪声数据进行分析后认为,Lg波成分约占49.4%,但众多学者的背景噪声互相关叠加数据中并未出现Lg波。丁文秀等[3]利用传统的背景噪声数据处理方法,在Rayleigh波之前发现了2组不太清晰的Lg1和Lg2波震相。
部分学者认为,在传统的背景噪声数据处理中,振幅信息归一化仅保留了波形数据的相位信息,后续的互相关叠加不能恢复出正确的振幅信息[4-6]。而Lg波的振幅谱是计算Q值的重要数据,如果能从背景噪声数据中恢复出Lg波的振幅信息,就可以摆脱传统Lg波Q值计算对地震事件的依赖,有助于获得更好路径覆盖率和更高分辨率的Q值分布。
目前,背景噪声的研究主要以相位信息为主,对于背景噪声振幅信息恢复的相关研究较少。在传统的背景噪声处理中,为削弱地震事件对背景噪声数据的干扰,对地震信号进行时域归一化处理(如one-bit方法、时间窗归一化方法等)后仅保留了波形的相位信息,其振幅信息被归一化,而是否能从背景噪声中重建经验格林函数的振幅信息存在争议[4-10]。因此,如何从背景噪声数据中提取清晰的Lg波及如何恢复出Lg波的振幅信息是本文主要探讨的科学问题。
1 数据选取由于背景噪声中Lg波震相出现在台间距约450 km以外的区域[3],本文选取鄂、湘、粤地区部分地震台站2 a(2013~2014年)的连续波形数据作为研究对象,台站间最大跨度约1 300 km,以保证台间距≥450 km的需求。连续波形数据来源于中国测震台网数据备份中心,采样率为1 Hz,由于天然地震中的Lg波在垂直分量和水平分量都能较好地显示,仅选取垂直分量作为本文的研究对象。
2 背景噪声数据处理由于采用传统背景噪声数据处理方式识别出的Lg波震相不太清晰[3],且振幅归一化处理后不能恢复出Lg波的振幅信息,本文在参照传统背景噪声数据处理方法[1]和Rayleigh波振幅信息提取研究[6, 9-10]的基础上,将数据处理划分为以下几步:
1) 单台数据预处理。提取单台以d为单位的垂直(Z)分量连续波形,进行去除仪器响应、去均值、去趋势和滤波处理。由于5~20 s微震频带中背景噪声以基阶面波(Rayleigh波和Love波)为主[11],传统的背景噪声数据处理通常去除周期≤5 s的高频成分。而Lg波属于短周期面波,普遍认为其周期为0.5~6 s,考虑到Lg波的周期特征和本文所用数据的采样率,本文选取的滤波参数为2.5~8 s。
2) 剔除地震事件和异常数据。本文采用剔除地震事件和异常数据的方法替代振幅归一化,具体做法为:①参考周连庆[10]关于背景噪声Rayleigh波振幅校正的做法,按照每个连续波形数据的长度建立相应的标识数据,并将标识数据设置为1,通过标识来区分是否参与互相关计算。当标识为1时,所对应的波形数据参与计算; 当标识为-1时,所对应的波形数据为地震事件和异常数据,不参与计算。②收集研究区域的地震目录,依据地震走时数据将地震波形数据设置为0,对应的标识数据设置为-1。③为了快速、简便地剔除异常数据和小震事件,本文通过测试采用台站振幅均方根RMS为参考基准值,即计算单台1 d连续波形振幅均方根RMS,并获取该台站2 a的平均振幅均方根RMS; 以RMS为参考基准值,采用滑动时间窗(窗长为20 s)计算每个窗的RMSw,如果RMSw>RMS,则将该窗内的标识数据设置为-1。④待滑动窗检索完毕,将标识为-1的波形数据剔除,即设置为0。图 1为ZUX台1 d的原始波形数据(图 1(a)、1(b))在剔除地震事件后的波形数据(图 1(c)、1(d))及对应的标识信息(图 1(e)、1(f)),其中图 1(b)、1(d)、1(f)分别为图 1(a)、1(c)、1(e)的局部放大波形。有学者用所有台站数据每个时间窗中数据的振幅均方根值为归一化因子,对时间窗中的波形数据进行归一化处理[6, 10],本文为最大程度地保留原始振幅信息,没有对其进行归一化处理。

|
图 1 ZUX台Z分量波形数据 Fig. 1 Z-component waveform data of ZUX station |
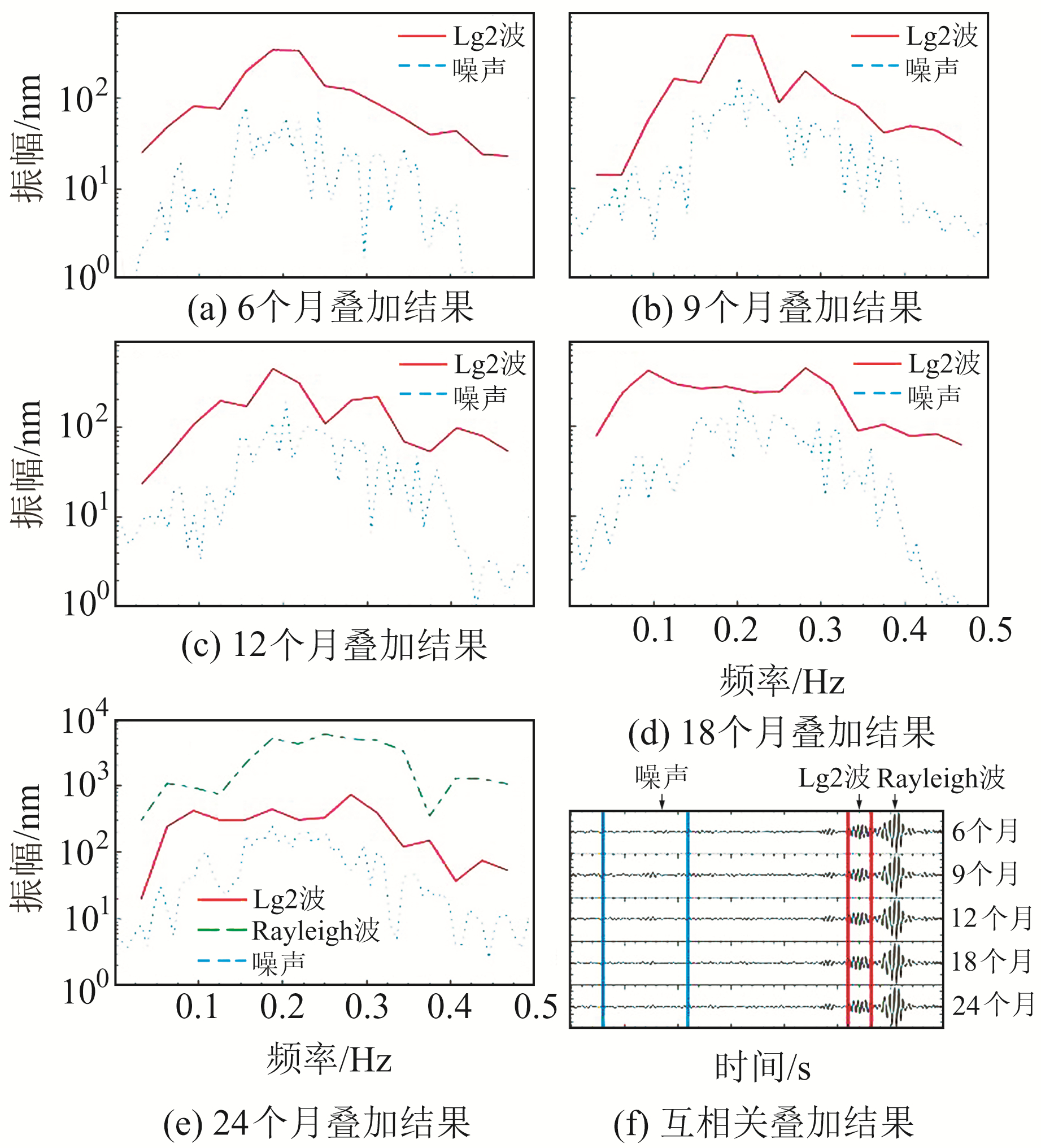
3) 互相关叠加。互相关叠加处理方法与传统的背景噪声数据处理策略一致,考虑到每个台站对的互相关叠加结果可能是由不同长度、不同天数的数据叠加得到,添加了标识数据的互相关叠加。标识数据互相关叠加后,在时间域对应的振幅大小就是叠加时所使用的实际波形数据,这一步是为后续的背景噪声叠加时间长度校正作准备。图 2为HUD-LCH台对6、9、12、18、24个月的互相关叠加结果,由图可知,对于HUD-LCH台对而言,6个月的互相关叠加结果就可以展现出Lg波。图 3为Lg波和噪声的振幅谱,可以看出,6~24个月Lg波的振幅谱均大于噪声振幅谱,证明了Lg波叠加信号的可靠性。

|
图 2 HUD-LCH台站对6、9、12、18、24个月互相关叠加结果 Fig. 2 Cross-correlation and stack results of HUD-LCH station of 6, 9, 12, 18, 24 months |
|
图 3 Lg波和噪声的振幅谱 Fig. 3 Lg-wave and noise spectra |
图 4为LCH台与部分台对24个月的波形互相关叠加数据,结合图 2~4可以看出,24个月的互相关叠加结果中正、负分支的Rayleigh波和Lg波并没有对称分布,这可能与噪声源的不对称分布有关[6, 12]。

|
图 4 LCH台与部分台对24个月互相关叠加结果 Fig. 4 24 months cross-correlation and stack results of LCH station and other stations |
目前,背景噪声振幅信息的恢复主要是针对Rayleigh波振幅的[6, 9, 13-14],普遍认为,背景噪声源分布非常不均匀,背景噪声互相关叠加数据的振幅不能直接用于计算,因此振幅校正是非常有必要的[6, 14-15]。Lin等[9]通过将Rayleigh波的衰减测量数据与内华达州地震及怀俄明州煤矿爆炸后观测到的振幅衰减进行对比认为,只要对背景噪声相互关叠加时间长度及几何扩散、噪声源强度的方位角变化和场地效应进行校正,便可在背景噪声中提取出振幅信息。
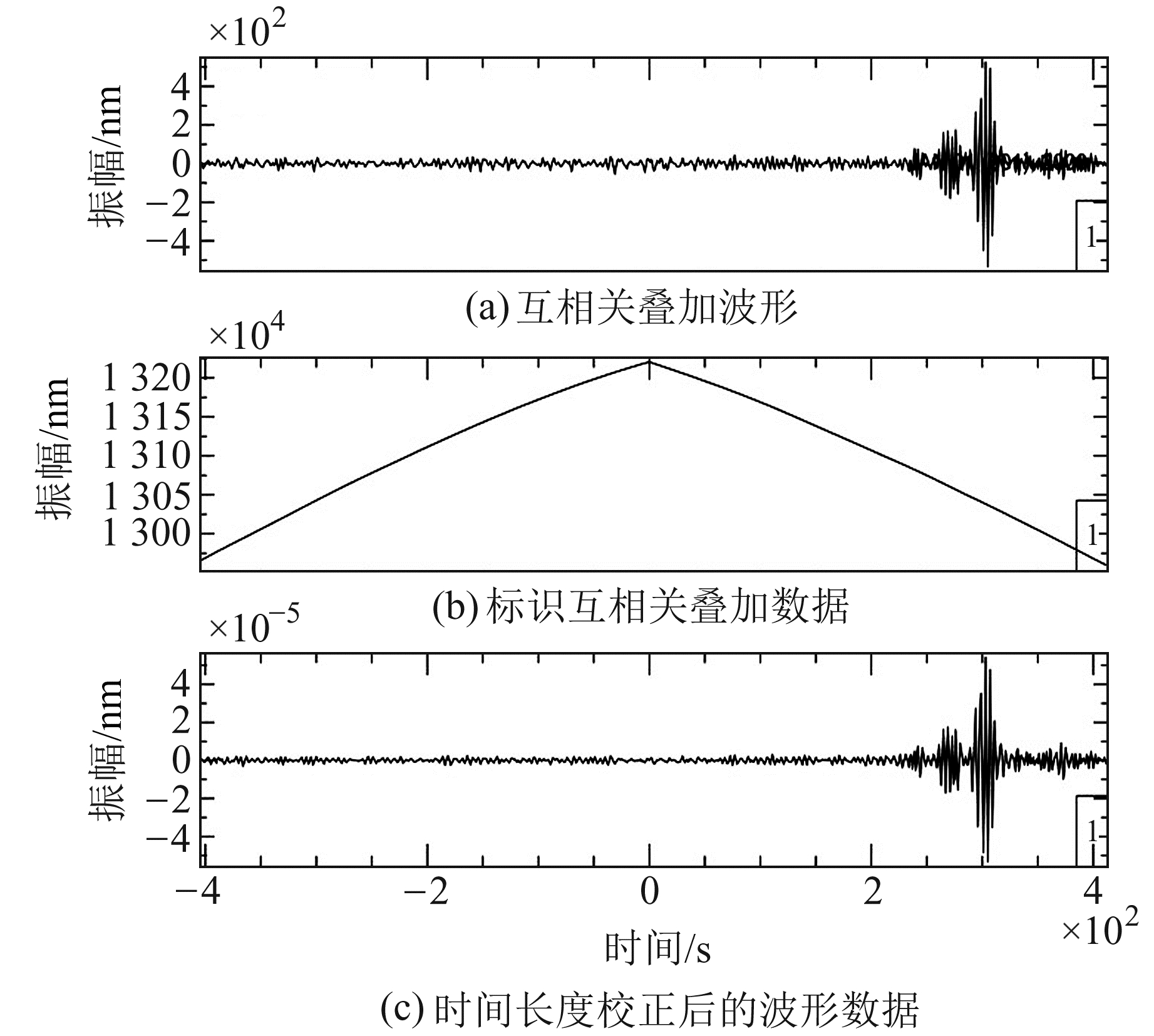
3.1 互相关叠加时间长度校正由于剔除地震信息后有可能造成同一天不同台站参与互相关的波形数据点数不同,而不同的台对最终参与叠加的天数也有可能不同,且数据互相关叠加的实际波形数据的点数和天数对振幅信息的影响非常显著。因此建立标识数据,标识数据互相关叠加结果的大小对应了背景噪声波形互相关叠加时使用的实际波形数据点数和叠加天数。参照Rayleigh波振幅的校正处理方法[10],将背景噪声互相关叠加数据除以对应的标识数据互相关叠加结果,得到经过校正后的波形数据,图 5为HUD-LCH台对互相关叠加波形、标识互相关叠加数据和互相关叠加时间长度校正后的波形数据。
|
图 5 HUD-LCH台对波形数据 Fig. 5 Waveform data of HUD-LCH stations |
噪声源分布的不均匀及噪声源强度的变化和不确定性是影响振幅恢复的关键因素[6],而双台法[16-18]为减弱噪声源和几何扩散的影响提供了途径,在双台法基础上发展起来的双台双震源法[19]还可以消除场地效应的影响。Lg波的振幅可以表示为[18]:
| $ A(f, \mathit{\Delta }) = S(f)G(\mathit{\Delta })\mathit{\Gamma }(f, \mathit{\Delta })P(f)r(f) $ | (1) |
| $ G(\mathit{\Delta }) = {\left( {{\mathit{\Delta }_0}\mathit{\Delta }} \right)^{ - \frac{1}{2}}} $ | (2) |
| $ \Gamma(f, \Delta)=\exp \left[-\frac{\pi f}{V}\left(\int_{i}^{j} \frac{\mathrm{d} s}{Q(x, y, f)}\right)\right] $ | (3) |
式中,S(f)为震源函数,G(Δ)为几何扩散因子,P(f)为台基响应函数,r(f)为随机效应,Г(f, Δ)为衰减函数,Q(x, y, f)为Lg波的Q值,V为Lg波的群速度。对于同一个天然地震事件a而言,如果2个台站i和j的方位角偏差小于一定的角度θ,即可近似认为该地震事件与这2个台站在一条直线上[16, 18]。通过提取2个台站间同一震源的Lg波振幅比(式(4)),并校正震中距比率的平方根,即可消除震源和几何扩散效应[16-18]:
| $ \frac{{{A_{aj}}}}{{{A_{ai}}}} = {\left( {\frac{{{\mathit{\Delta }_{aj}}}}{{{\mathit{\Delta }_{ai}}}}} \right)^{ - \frac{1}{2}}}\exp \left[ { - \frac{{\pi f}}{V}\left( {\int_i^j {\frac{{{\rm{d}}s}}{{Q(x, y, f)}}} } \right)} \right]\frac{{{P_j}}}{{{P_i}}} $ | (4) |
式中,Δai、Δaj分别为地震事件a到台站i、j的震中距。
对于2个天然地震事件a和b,如果2个台站i和j的方位角偏差小于一定的角度θ,即可近似认为这2个天然地震事件与2个台站在一条直线上[19]。双台双震源法(式(5))可消除震源、几何扩散和场地效应的影响:
| $ \begin{array}{l} \frac{1}{{Q(f)}} = \left\{ {\frac{v}{{\pi f\left[ {\left( {{\mathit{\Delta }_{bi}} - {\mathit{\Delta }_{bj}}} \right) - \left( {{\mathit{\Delta }_{ai}} - {\mathit{\Delta }_{aj}}} \right)} \right]}}} \\ \;\;\;\;\;\;\;\;\;\ln \left[ {\left( {\frac{{{A_{ai}}}}{{{A_{aj}}}}\frac{{{A_{bj}}}}{{{A_{bi}}}}} \right){{\left( {\frac{{{\mathit{\Delta }_{ai}}}}{{{\mathit{\Delta }_{aj}}}}\frac{{{\mathit{\Delta }_{bj}}}}{{{\mathit{\Delta }_{bi}}}}} \right)}^m}} \right]\right\} \end{array} $ | (5) |
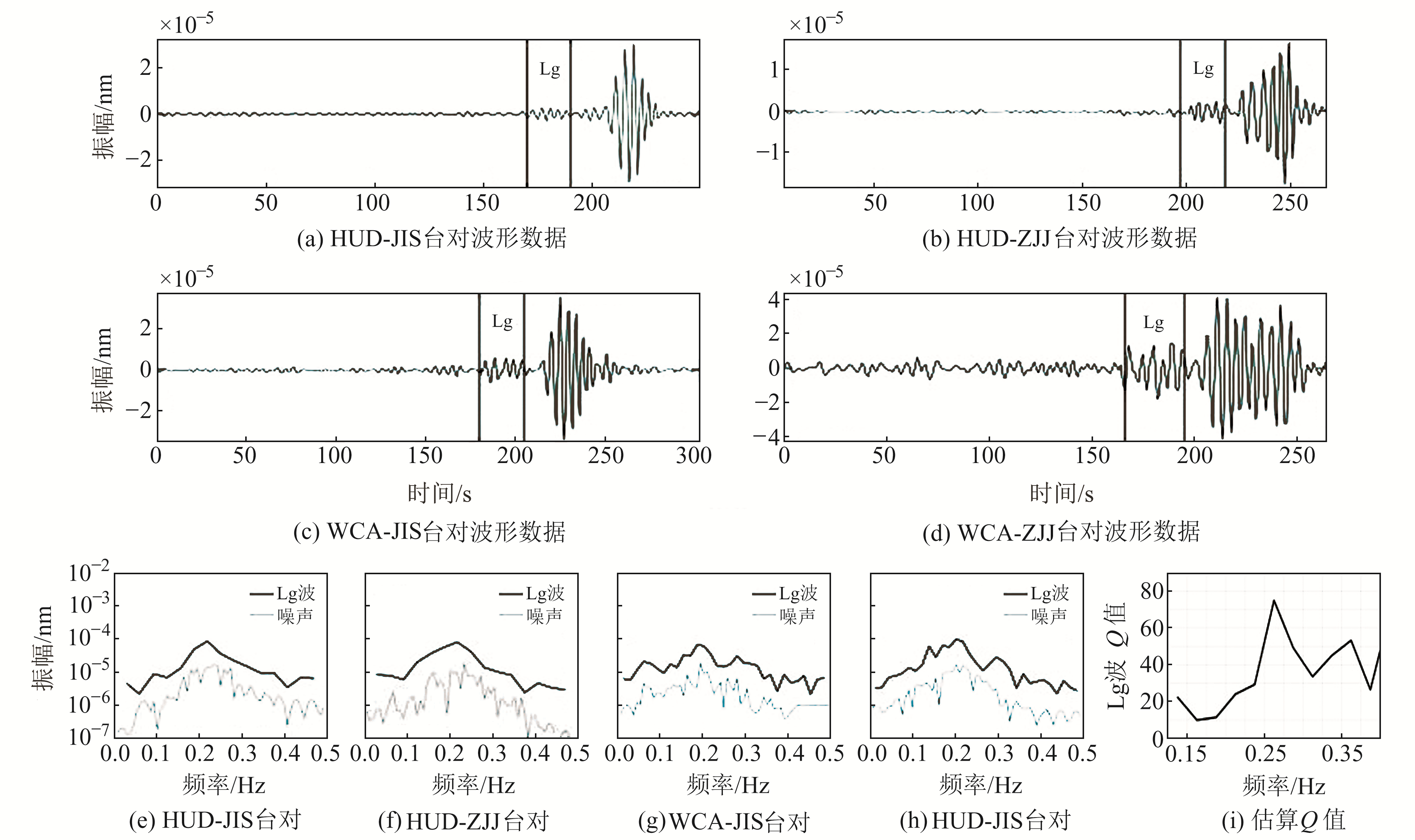
图 6(a)~6(d)为互相关叠加时间长度校正后4个台对的波形数据,如果将HUD台和WCA台当作震源,JIS台和ZJJ台当作接收台站,采用双台双震源法即可消除震源、几何扩散和场地效应的影响,估算的Q值见图 6(i)。
|
图 6 台对互相关叠加时间长度校正后的波形数据、Lg波和噪声振幅谱及估算Q值 Fig. 6 Waveform data corrected by cross correlation stack time length and Lg-wave, noise amplitude spectrum by stations and estimate Q |
本文研究表明,对地震背景噪声数据进行适当的处理,可在互相关叠加数据中识别出Lg波,噪声源的分布不均匀及噪声源强度的变化和不确定性是影响Lg波振幅恢复的主要因素。本文通过双台双震源法消除震源、几何扩散和场地效应的影响,并估算了Q值。背景噪声数据中Lg波的识别及振幅信息的校正与提取,有助于科研工作者摆脱目前Lg波Q值研究对地震事件的依赖。
致谢: 感谢中国测震台网数据备份中心提供连续波形数据。
| [1] |
Bensen G B, Ritzwoller M H, Barmin M P, et al. Processing Seismic Ambient Noise Data to Obtain Reliable Broad-Band Surface Wave Dispersion Measurements[J]. Geophysical Journal International, 2007, 169(3): 1 239-1 260 DOI:10.1111/j.1365-246X.2007.03374.x
(  0) 0) |
| [2] |
Koper K D, Seats K, Benz H. On the Composition of Earth's Short-Period Seismic Noise Field[J]. Bulletin of the Seismological Society of America, 2010, 100(2): 606-617 DOI:10.1785/0120090120
(  0) 0) |
| [3] |
丁文秀, 付媛媛, 高原, 等. 秦岭-大别及邻区背景噪声的瑞利波层析成像[J]. 地球物理学报, 2017, 60(8): 2 959-2 968 (Ding Wenxiu, Fu Yuanyuan, Gao Yuan, et al. Phase Velocity Tomography of Rayleigh in Qinling-Dabie and Its Adjacent Areas Using Ambient Seismic Noise[J]. Chinese Journal of Geophysics, 2017, 60(8): 2 959-2 968)
(  0) 0) |
| [4] |
Larose E, Roux P, Campillo M. Reconstruction of Rayleigh-Lamb Dispersion Spectrum Based on Noise Obtained from an Air-Jet Forcing[J]. The Journal of the Acoustical Society of the America, 2007, 122(6): 3 437-3 444 DOI:10.1121/1.2799913
(  0) 0) |
| [5] |
Prieto G A, Lawrence J F, Beroza G C. Anelastic Earth Structure from the Coherency of the Ambient Seismic Field[J]. Journal of Geophysical Research Solid Earth, 2009, 114(B7)
(  0) 0) |
| [6] |
Weaver R L. On the Amplitudes of Correlations and the Inference of Attenuations, Specific Intensities and Site Factors from Ambient Noise[J]. Comptes Rendus Geoscience, 2011, 343(8-9): 615-622 DOI:10.1016/j.crte.2011.07.001
(  0) 0) |
| [7] |
Cupillard P, Capdeville Y. On the Amplitude of Surface Waves Obtained by Noise Correlation and the Capability to Recover the Attenuation: A Numerical Approach[J]. Geophysical Journal International, 2010, 181(3): 1 687-1 700
(  0) 0) |
| [8] |
Cupillard P, Stehly L, Romanowicz B. The One-Bit Correlation: A Theory Based on the Concepts of Coherent and Incoherent Noise[J]. Geophysical Journal International, 2011, 184(3): 1 397-1 414 DOI:10.1111/j.1365-246X.2010.04923.x
(  0) 0) |
| [9] |
Lin F C, Ritzwoller M H, Shen W S. On the Reliability of Attenuation Measurements from Ambient Noise Cross-Correlations[J]. Geophysical Research Letters, 2011, 38(11)
(  0) 0) |
| [10] |
周连庆. 地球介质衰减特性层析成像[D]. 北京: 中国地震局地球物理研究所, 2016 (Zhou Lianqing. Attenuation Tomography of the Earth Media[D]. Beijing: Institute of Geophysics, CEA, 2016)
(  0) 0) |
| [11] |
徐义贤, 罗银河. 噪声地震学方法及其应用[J]. 地球物理学报, 2015, 58(8): 2 618-2 636 (Xu Yixian, Luo Yinhe. Methods of Ambient Noise-Based Seismology and Their Applications[J]. Chinese Journal of Geophysics, 2015, 58(8): 2 618-2 636)
(  0) 0) |
| [12] |
Stehly L, Campillo M, Shapiro N M. A Study of the Seismic Noise from Its Long-Range Correlation Properties[J]. Journal of Geophysical Research Solid Earth, 2006, 111(B10)
(  0) 0) |
| [13] |
Lin F C, Tsai V C, Ritzwoller M H. The Local Amplification of Surface Waves: A New Observable to Constrain Elastic Velocities, Density, and Anelastic Attenuation[J]. Journal of Geophysical Research Solid Earth, 2012, 117(B6)
(  0) 0) |
| [14] |
Bowden D C, Tsai V C, Lin F C. Amplification and Attenuation across USArray Using Ambient Noise Wavefront Tracking[J]. Journal of Geophysical Research Solid Earth, 2017, 122(12): 10 086-10 101 DOI:10.1002/2017JB014804
(  0) 0) |
| [15] |
Tsai V C. Understanding the Amplitudes of Noise Correlation Measurements[J]. Journal of Geophysical Research Solid Earth, 2011, 116(B9)
(  0) 0) |
| [16] |
Xie J K, Gok R, Ni J, et al. Lateral Variations of Crustal Seismic Attenuation along the Indepth Profiles in Tibet from Lg Q Inversion[J]. Journal of Geophysical Research Solid Earth, 2004, 109(B10)
(  0) 0) |
| [17] |
Singh C, Shekar M, Singh A, et al. Seismic Attenuation Characteristics along the Hi-Climb Profile in Tibet from Lg Q Inversion[J]. Bulletin of the Seismological Society of America, 2012, 102(6): 783-789
(  0) 0) |
| [18] |
赵连锋, 谢小碧, 王卫民, 等. 中国东北和朝鲜半岛地区地壳Lg波宽频带衰减模型[J]. 地球物理学报, 2018, 61(3): 856-871 (Zhao Lianfeng, Xie Xiaobi, Wang Weimin, et al. A Broadband Crustal Lg Wave Attenuation Model in Northeast China and the Korean Peninsula[J]. Chinese Journal of Geophysics, 2018, 61(3): 856-871)
(  0) 0) |
| [19] |
Bao X Y, Sandvol E, Ni J, et al. High Resolution Regional Seismic Attenuation Tomography in Eastern Tibetan Plateau and Adjacent Regions[J]. Geophysical Research Letters, 2011, 38(16)
(  0) 0) |
2. Hubei Key Laboratory of Earthquake Early Warning, 48 Hongshance Road, Wuhan 430071, China
 2021, Vol. 41
2021, Vol. 41

