2. 中国科学院大学,北京市玉泉路19号甲,100049
剪切波分裂测量是研究地震各向异性最成熟的方法之一[1],但由于剪切波分裂的结果是其传播路径上不同深度范围内所有各向异性信息的叠加,因此无法获知各向异性的深度分布信息[2]。在利用散射面波研究传播介质的各向异性时,为提高识别度,使其他高频干扰信号(如交通信号等)被最大程度地压制,通常使用低频(>70 s)准勒夫(Quasi-Love)波信号[3-4]。目前Quasi-Love波已被应用于日本千岛群岛、阿留申岛中部、汤加群岛等环太平洋俯冲带地区的上地幔各向异性梯度特性研究[5-7],同时根据中国西藏地区台站记录的Quasi-Love波,证实了中国西藏地区存在地幔和地壳垂直耦合的边界状态[8]。然而,同剪切波方法相比,Quasi-Love波的应用还不够广泛。
由于小波变换更适合处理如地震信号类的非平稳信号,本文提出使用基于标准时频变换[9-10](normal time-frequency transform,NTFT)的方法探测Quasi-Love波。NTFT是一种新的小波变换,与传统的小波变换相比具有“无为原理”[11]属性和强抗噪声能力,目前已被成功应用于海潮信号分析和预测[12]、长周期地球自转信号预测[13]及GPS钟差信号分析[14]等地学领域。本文基于NTFT谱系数定义了评价2个信号相关程度的相似度概念,并使用该方法估计Quasi-Love波和Love波的相关性及二者的延时,首先在NTFT的基础上引出相似度的概念,通过仿真实验评价其抗噪声能力,并将其与广泛使用的互相关法进行比较,再将NTFT方法应用到Quasi-Love波的识别中。
1 方法本文首先介绍NTFT的基本理论,相似度的概念是基于NTFT时频谱定义的,所以在NTFT的基础上引出相似度的定义,并通过仿真信号测试相似度法在高背景噪声下的性能。
1.1 标准时频变换对于一个复时间函数f(t)∈C,其标准时频变换为:
| $ \psi(t, \tilde{\omega})=\int_{-\infty}^{+\infty} f(t) \bar{\psi}(t-\tau, \tilde{\omega}) \mathrm{d} t \quad \tilde{\omega}, \tau \in R $ | (1) |
式中,τ和ω分别为平移时间和频率因子,ψ为NTFT的标准核函数,ψ为对标准核函数取共轭运算,C和R分别为复数域和实数域。标准核函数满足以下条件:
| $ \hat{\psi}(\omega, \tilde{\omega})=\int_{-\infty}^{+\infty} \psi(t, \tilde{\omega}) \exp (-\mathrm{i} w t) \mathrm{d} t $ | (2) |
| $ \hat{\psi}(\omega, \tilde{\omega})=|\hat{\psi}(\omega, \tilde{\omega})|=\text { maximum }=1 \Leftrightarrow \omega=\tilde{\omega} $ | (3) |
| $ \hat{\psi}(\omega, \tilde{\omega})=|\hat{\psi}(\omega, \tilde{\omega})|<1 \Leftrightarrow \omega \neq \tilde{\omega} $ | (4) |
其中,式(2)为核函数的傅里叶变换; 而对于式(3)的频谱函数
估计信号相关性最常用的方法是互相关(cross correlation,CC)法,本文基于NTFT时频谱定义类似的算法,使用信号的频率和时域特征求2个信号的相关性。由于NTFT谱系数的模等于信号在时域中的实际振幅,所以这种基于NTFT时频谱的算法直接反映了信号的“相似程度”,即为相似度(similarity coefficient,SC)法。对于2个时间函数f1(t)和f2(t),其相似度函数ρ(s)定义为:
| $ \rho(s)=\frac{\iint_{S} \operatorname{Re} \psi f_{1}(\tau-s, \tilde{\omega}) \operatorname{Re} \psi f_{2}(\tau, \tilde{\omega}) \mathrm{d} \tau \mathrm{d} \tilde{\omega}}{\sqrt{\iint_{S}\left(\operatorname{Re} \psi f_{1}(\tau-s, \tilde{\omega})\right)^{2} \mathrm{~d} \tau \mathrm{d} \tilde{\omega} \iint_{S}\left(\operatorname{Re} \psi f_{2}(\tau, \tilde{\omega})\right)^{2} \mathrm{~d} \tau \mathrm{d} \tilde{\omega}}} $ | (5) |
式中,ψf1和ψf2为函数f1(t)和f2(t)的标准时频变换,Reψ为NTFT谱系数ψ(t,
为了测试相似度法的抗噪声能力,仿真2个信号的时间序列,在无噪声和加入噪声的情况下分别使用本文提出的SC法和经典CC法计算两者的相关性,根据计算结果评价SC法的抗噪性能。测试使用的仿真信号表达式为:
| $ \left\{\begin{array}{l} f_{1}(t)=\sin (2 \pi \omega(1+t / 30) t)+\varepsilon_{1} \\ f_{2}(t)=\sin (2 \pi \omega(1+(t+n) / 30)(t+n))+\varepsilon_{2} \end{array}\right. $ | (6) |
式中,ε1和ε2为高斯白噪声,n为时间延迟。设置初始频率ω=1,采样周期为0.1 s,时间延迟n=800 s,并加入噪声水平为-2.5 dB的高斯白噪声。2个仿真信号具有相同的表达式,在时域中有相同的波形,仿真信号的初始频率为1 Hz,随着时间的增加频率逐渐增大。图 1(a)为仿真信号的FFT振幅谱,可以看出,仿真信号的主频为1~2 Hz; 图 1(b)为仿真信号的NTFT时频谱,可以看出,时频谱随时间逐渐增大,2个信号的延时为800 s。在原始信号中加入较高水平的高斯白噪声,图 2(a)为加入-2.5 dB高斯噪声后仿真信号的FFT振幅谱,可以看到,加入噪声后影响较大,信号的主频已经不明显; 由图 2(b)可以发现,加入噪声后NTFT时频谱也受到一定程度的影响,但基本还能分辨出有2个周期随时间衰减的信号。分别利用SC法和CC法对2个信号的相关性进行估计,图 3(a)和3(b)分别为无噪声和较高噪声情况下的结果,由图可知,无噪声时2种方法计算的结果几乎重合,在延时为800 s处均取得极值,最大值约为1,与理论值一致,说明2种方法的性能一致; 而在较高噪声水平下,SC法估计2个仿真信号的相关系数约为0.8,最大值对应的时间延迟仍为800 s,而CC法已无法判断2个信号是否为同一个信号。实验结果表明,SC法具有较强的抗噪声能力,在极低的信噪比情况下依然能得出正确的结论,相较于CC法,使用SC法有利于提高对相似信号识别的准确度。
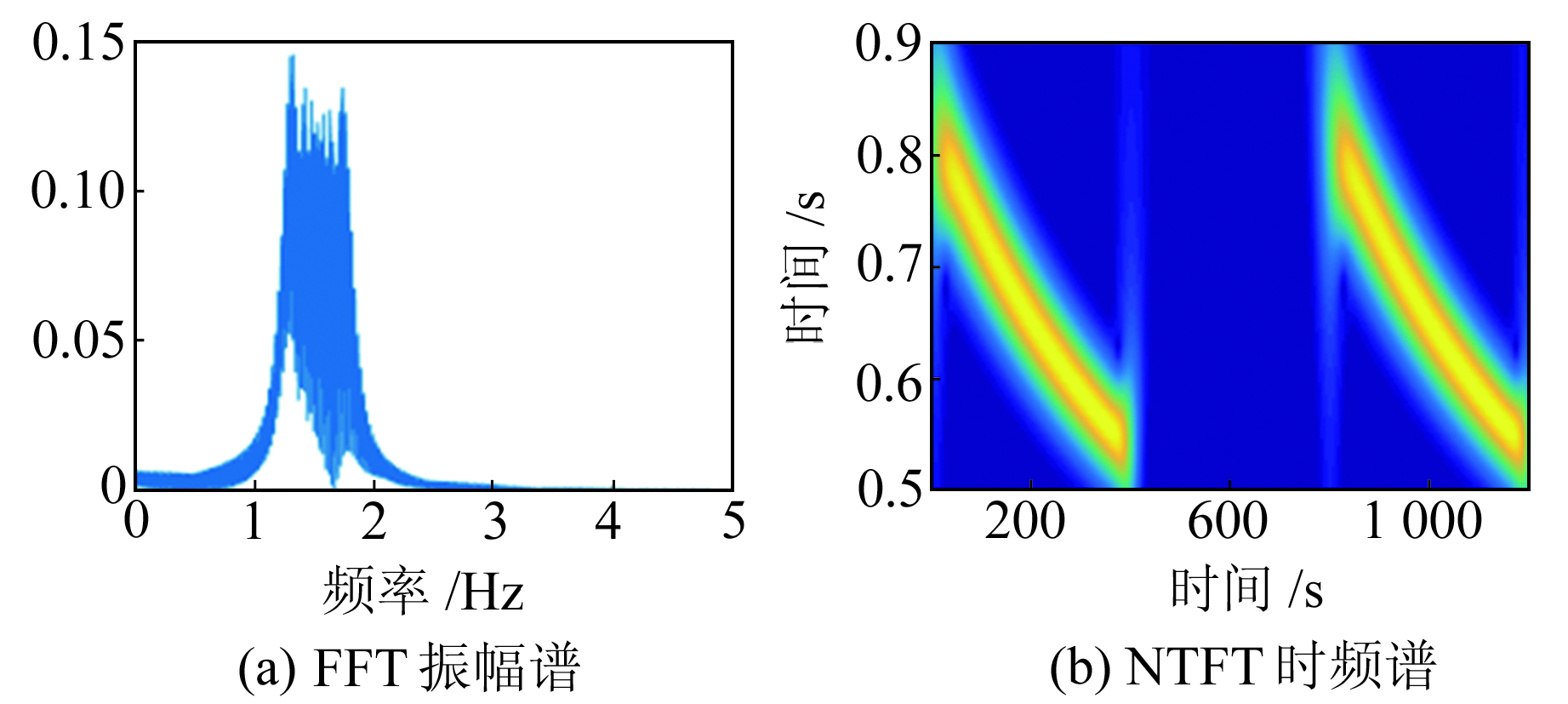
|
图 1 无噪声信号 Fig. 1 Signal without noise |
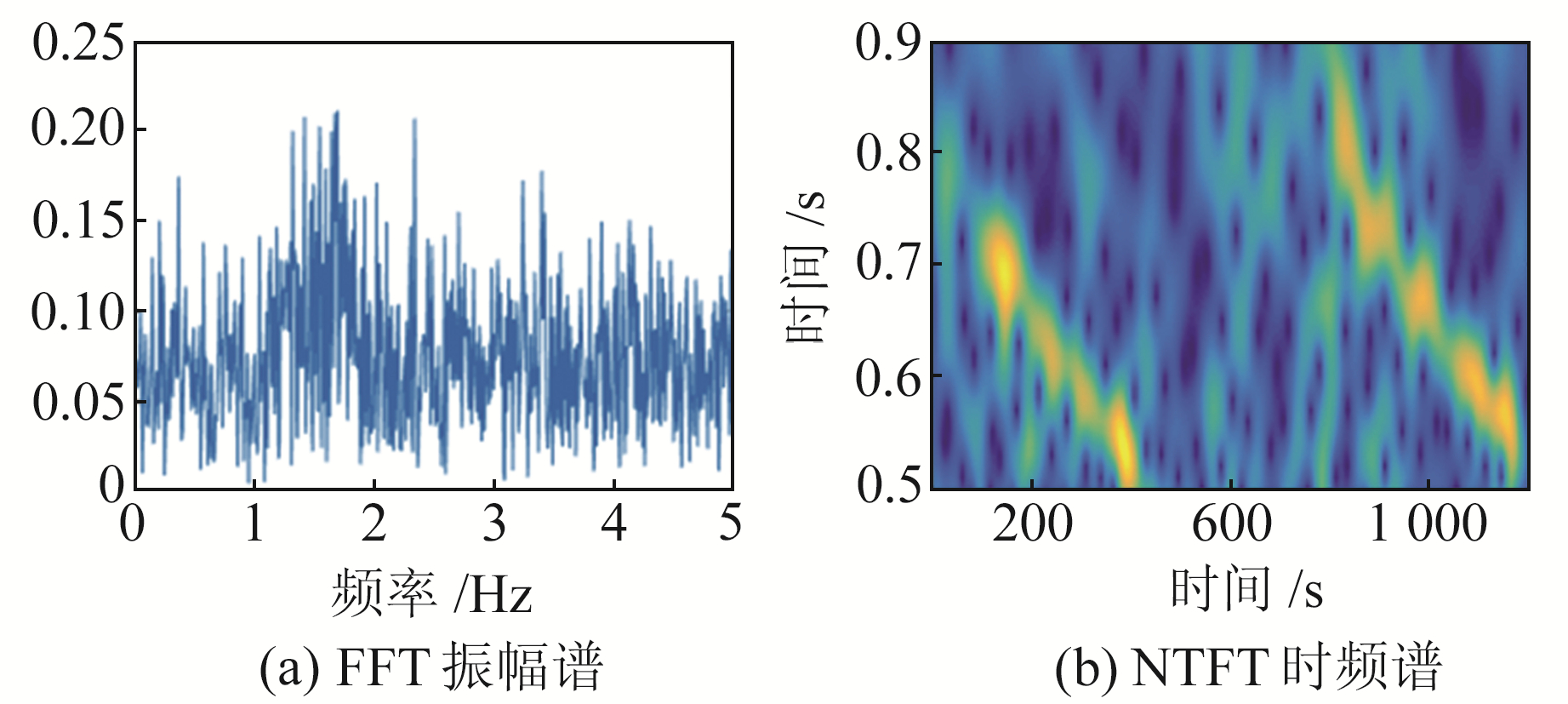
|
图 2 加入噪声后信号 Fig. 2 Signal with gaussian noise |

|
图 3 SC法和CC法估计信号的相关性 Fig. 3 Correlation of signals estimated by SC method and CC method |
本文利用2004-12-26苏门答腊MW9.0(Global CMT)地震激发的面波数据研究Quasi-Love波,选用意大利半岛的ELBR台和CSTR台记录的地震数据,数据来源于IRIS数据管理中心,采样率为50 Hz,2个台站的震中距分别为84°和83°。为比较Quasi-Love波与Love波能量的大小,本文将水平分量数据旋转至径向(R)和切向(T),同时为减小计算量,将原始波形数据降采样至1 Hz。为在NTFT时频谱中观测Quasi-Love波,分别将2个台站记录的Z向和T向数据作NTFT处理,周期范围为50~200 s,核函数设计成标准Morlet小波[15],并选择Love波到时附近的数据段进行观察,结果见图 4。可以看到,2个台站T向的NTFT时频谱十分相似,均出现了相同信号,该信号即为Love波; 而Z向的NTFT时频谱差异较大,ELBR台在1 300~1 400 s(Love波附近)出现了一个较强的信号,CSTR台则缺少该信号,推断该信号为Quasi-Love波。为验证该推断,利用常规高阶FIR滤波器对2个台站的面波数据进行带通滤波处理,滤波器阶数为110,滤波范围为10~20 mHz(50~100 s),并将结果与NTFT时频谱进行对比,图 5为2个台站Z向和T向的地震波数据经低频滤波后的结果。从图 5可以清晰地观测到Love波和Rayleigh波,并且在ELBR台Z向数据中发现有微弱的异常波形出现在Rayleigh波之前,根据对Quasi-Love波的观测经验可知,该异常波形即为Quasi-Love波,CSTR台则无类似异常波形信号。

|
图 4 ELBR台和CSTR台Z向和T向的NTFT时频谱 Fig. 4 NTFT time-frequency spectra of the Z component and T component from ELBR station and CSTR station |
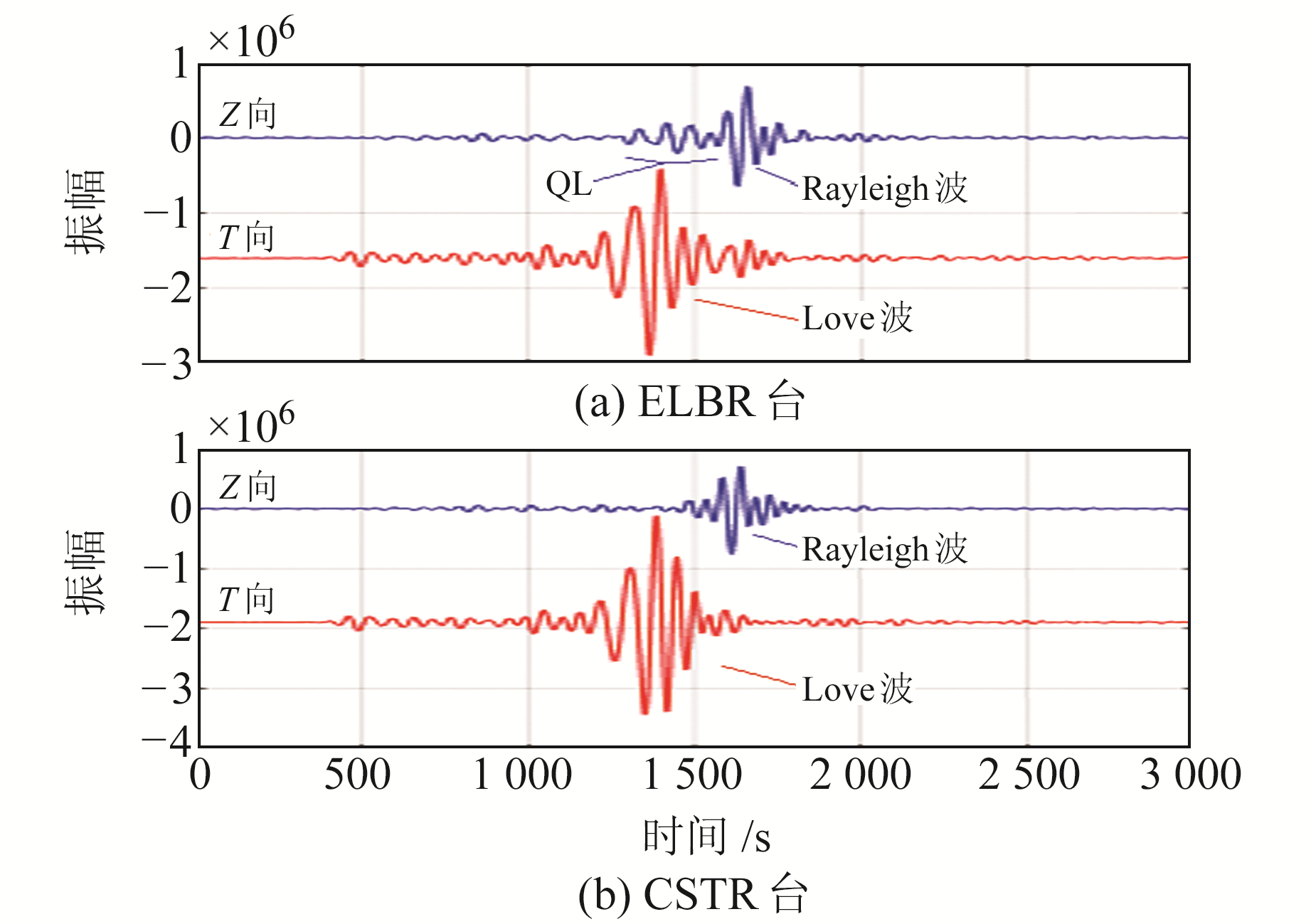
|
图 5 ELBR和CSTR台Z向和T向数据滤波后的波形 Fig. 5 The filtered waveforms of the Z and T components of ELBR station and CSTR station |
NTFT时频谱中观测到的Quasi-Love波和由传统方法得到的结果一致,但NTFT时频谱中的更加明显,有利于信号的识别。另外,NTFT时频谱显示出Quasi-Love波的时频特征,利用传统带通滤波器对信号进行滤波后容易引起信号的相位偏移,而NTFT时频谱中的Quasi-Love波不会出现相位偏移,这对估计Quasi-Love波的延时十分重要。使用SC法估算Quasi-Love波的延时,并利用式(5)估计ELBR台T向数据中Love波和Z向数据中Quasi-Love波的相关性,结果见图 6。由图可知,2个信号的相关性峰值为0.6,对应的时间延迟为2 s,说明Quasi-Love波和Love波几乎同时到达台站,且Quasi-Love波的散射体应在台站附近,说明台站附近存在各向异性梯度介质; 而长周期面波通常对上地幔敏感,说明ELBR台附近的上地幔存在各向异性梯度。

|
图 6 SC法估计ELBR台Quasi-Love波和Love波的相关性 Fig. 6 SC method estimates the correlation between Quasi-Love wave and Love wave of ELBR station |
本文利用NTFT方法识别Quasi-Love波信号,基于NTFT时频谱系数定义了估计2个信号相关性的SC法,并使用SC法估计了Quasi-Love波的延时。与传统方法相比,NTFT方法在未对信号作任何滤波处理的情况下成功识别出了Quasi-Love波信号,并能在NTFT时频谱中观察到信号的频率随时间的变化。另外,本文通过NTFT方法研究了意大利半岛2个台站记录的2004年苏门答腊大地震的面波数据,在ELBR台识别出Quasi-Love波,并根据SC法计算了Quasi-Love波的延时,但未对其产生机理作详细研究。Quasi-Love波的出现同上地幔各向异性梯度存在紧密联系,而地震各向异性是地球动力学研究的重要内容。目前各向异性探测工具以剪切波分裂技术为主,但随着高质量地震波数据的轻松获取,Quasi-Love波在地球动力学研究方面的应用具有较好的前景。
致谢: 本文使用的地震波数据来源于地震学研究联合会(IRIS)数据管理中心(DMC),部分图件由GMT软件绘制,在此表示感谢。
| [1] |
Savage M K. Seismic Anisotropy and Mantle Deformation: What Have We Learned from Shear Wave Splitting?[J]. Reviews of Geophysics, 1999, 37(1): 65-106 DOI:10.1029/98RG02075
(  0) 0) |
| [2] |
Long M D, Silver P G. The Subduction Zone Flow Field from Seismic Anisotropy: A Global View[J]. Science, 2008, 319(5861): 315-318 DOI:10.1126/science.1150809
(  0) 0) |
| [3] |
Maupin V, Park J. Theory and Observations——Wave Propagation in Anisotropic Media[M]. Amsterdam: Elsevier, 2007
(  0) 0) |
| [4] |
Kobayashi R. Polarization Anomalies of Love Waves Observed in and around Japan[J]. Earth, Planets and Space, 2002, 54(4): 357-365 DOI:10.1186/BF03352425
(  0) 0) |
| [5] |
Park J, Levin V, Brandon M, et al. A Dangling Slab, Amplified Arc Volcanism, Mantle Flow and Seismic Anisotropy in the Kamchatka Plate Corner[M]. Washington D C: American Geophysical Union, 2013
(  0) 0) |
| [6] |
Kobayashi R, Nakanishi I. Location of Love-to-Rayleigh Conversion due to Lateral Heterogeneity or Azimuthal Anisotropy in the Upper Mantle[J]. Geophysical Research Letters, 1998, 25(7): 1 067-1 070 DOI:10.1029/98GL00651
(  0) 0) |
| [7] |
Levin V, Park J. Quasi-Love Phases between Tonga and Hawaii: Observations, Simulations, and Explanations[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B10): 24 321-24 331 DOI:10.1029/98JB02342
(  0) 0) |
| [8] |
Chen X J, Park J. Anisotropy Gradients from QL Surface Waves: Evidence for Vertically Coherent Deformation in the Tibet Region[J]. Tectonophysics, 2013, 608: 346-355 DOI:10.1016/j.tecto.2013.09.019
(  0) 0) |
| [9] |
Liu L T, Xu H Z. Inversion and Normalization of Time-Frequency Transform[J]. Applied Mathematics and Information Sciences, 2012, 6(1): 67-74
(  0) 0) |
| [10] |
柳林涛, 苏晓庆, 王国成. 标准时频变换探讨[J]. 导航定位学报, 2016, 4(4): 1-4 (Liu Lintao, Su Xiaoqing, Wang Guocheng. Discussion on Normal Time-Frequency Transform[J]. Journal of Navigation and Positioning, 2016, 4(4): 1-4)
(  0) 0) |
| [11] |
蔡松, 柳林涛, 王国成. 标准时频变换的潮汐预测初探[J]. 测绘科学, 2018, 43(7): 27-32 (Cai Song, Liu Lintao, Wang Guocheng. Primary Study of Tidal Level Prediction Using Normal Time-Frequency Transform[J]. Science of Surveying and Mapping, 2018, 43(7): 27-32)
(  0) 0) |
| [12] |
Cai S, Liu L T, Wang G C. Short-Term Tidal Level Prediction Using Normal Time-Frequency Transform[J]. Ocean Engineering, 2018, 156: 489-499 DOI:10.1016/j.oceaneng.2018.03.021
(  0) 0) |
| [13] |
Su X Q, Liu L T, Xu H Z, et al. Long-Term Polar Motion Prediction Using Normal Time-Frequency Transform[J]. Journal of Geodesy, 2014, 88(2): 145-155 DOI:10.1007/s00190-013-0675-7
(  0) 0) |
| [14] |
Wang G C, Liu L T, Xu A G, et al. On the Capabilities of the Inaction Method for Extracting the Periodic Components from GPS Clock Data[J]. GPS Solutions, 2018, 22(4): 1-14 DOI:10.1007/s10291-018-0757-3
(  0) 0) |
| [15] |
徐华君, 柳林涛, 罗孝文. 标准Morlet小波变换检测地球自由振荡[J]. 测绘学报, 2009, 38(1): 16-21 (Xu Huajun, Liu Lintao, Luo Xiaowen. Normal Morlet Wavelet Transform and Its Application to Detection of the Earth's Free Oscillations[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 16-21)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2021, Vol. 41
2021, Vol. 41


