2. 引力与固体潮国家野外观测研究站, 武汉市洪山侧路40号, 430071;
3. 中国地震局地震大地测量重点实验室, 武汉市洪山侧路40号, 430071;
4. 湖北省地震局, 武汉市洪山侧路40号, 430071
随机噪声具有强烈的随机性, 在地震资料中普遍存在[1], 因此无论是天然地震还是人工地震, 随机噪声的处理都是提高地震资料信噪比的关键之一。常用的地震信号随机噪声压制方法有拉东变换、经验模态分解、曲波变换与小波变换等[2], 其中小波变换具有多分辨率分析的特点, 能够同时表征信号在时域和频域的局部特性[3]。经小波分解得到小波系数后, 根据有效信号与随机噪声小波系数的不同而设定阈值, 对随机噪声的小波系数进行处理后再对小波系数进行重构, 可达到信号去噪的目的。
提升小波算法被称为“第二代小波”, 是一种基于时域运算的信号分析方法, 可克服经典小波降噪方法局部信息丢失的缺点[4]。对于小波阈值去噪, 阈值函数与阈值的选取对地震资料去噪的结果具有很大影响。经典的阈值函数包含硬阈值和软阈值, 其中硬阈值函数是当小波系数的绝对值大于设定的阈值时系数保持不变、小于阈值时系数为零, 这会导致其在阈值处不连续, 从而使重构信号产生一定的震荡; 而软阈值函数可克服硬阈值函数在阈值处不连续的缺点, 当小波系数的绝对值大于阈值时减去阈值, 小于阈值时则进行置零处理, 但经过软阈值处理的小波系数与实际小波系数存在恒定偏差, 从而影响重构信号的精度。
本文在经典软、硬阈值函数的基础上提出一种改进的阈值函数, 从理论上证明该阈值函数可克服经典阈值函数的不连续与存在恒定偏差的缺点, 并通过信号仿真证实经过该阈值函数处理后可很好地压制高斯白噪声, 提高含噪信号的信噪比。最后将改进阈值函数的提升小波算法运用于气枪震源, 分析其在人工震源去噪方面的可行性。
1 改进阈值函数的提升小波变换 1.1 提升小波Mallat算法利用多分辨率分析分解信号, 从而去除信号间的相关性, 而提升小波算法则是将信号分解为偶数采样点和奇数采样点[5]。由于相邻数据的相关性较强, 可通过奇数采样点估计偶数采样点, 再去除包含在偶数采样点中关于奇数采样点的信息, 从而消除信号间的相关性。提升小波算法的实现包含分裂(spilit)、预测(predict)和更新(update)。其中, 分裂是将原始信号Si按照序列的奇偶性分裂为2个互不相关的子集, 即偶数序列Se与奇数序列So。预测是利用原始信号相邻数据间的相关性, 用偶数序列Se与1个预测算子P来预测奇数序列So, 得到P(So), 并将奇数序列So与奇数序列预测值P(So)的差值di-1作为小波系数, 其中di-1=So-P(So)。更新则是为使分裂后得到的偶数序列Se保持原始信号的某些特性, 构造一个更新算子U(di-1)对其进行更新, 得到尺度系数ai-1[6]:
| $ a_{i-1}=S_{e}+U\left(d_{i-1}\right) $ | (1) |
对含噪地震信号进行一维离散小波分解, 得到一系列小波系数。由于有效信号在时间域或空间域具有一定的连续性, 而噪声信号则表现为随机性, 从而导致小波域中有效信号对应的小波系数值较大, 而噪声信号对应的小波系数值较小。根据该特点设置一个阈值, 将小于该阈值的小波系数去除, 即将噪声主导对应的小波系数去除, 再对剩余的小波系数进行重构, 达到去除噪声的目的, 因此阈值与阈值函数的选择具有重要意义:
| $ \lambda=\sigma \sqrt{2 \log N} $ | (2) |
| $ \sigma=\frac{\operatorname{median}\left(c d_{n}\right)}{0.674\;5} $ | (3) |
研究表明[3, 6-7], 随着分解层数的增加, 各层小波细节系数中噪声含量会逐渐减小, 因此阈值应当有所变化。经过一系列仿真实验, 本文使用一种改进的阈值, 具体公式为:
| $ \lambda=\frac{\sigma \sqrt{2 \log N}}{j} $ | (4) |
式(2)~式(4)中, λ为去噪阈值, σ为噪声强度, N为信号长度, cdn为小波分解后第n层高频小波系数, j为分解层数。
在得到阈值后, 可使用硬阈值函数和软阈值函数对小波系数进行处理。硬阈值函数表达式为:
| $ {\hat w_{j, k}} = \left\{ \begin{array}{l} \;\;0, \left| {{w_{j, k}}} \right| < \lambda \\ {w_{j, k}}, \left| {{w_{j, k}}} \right| \ge \lambda \end{array} \right. $ | (5) |
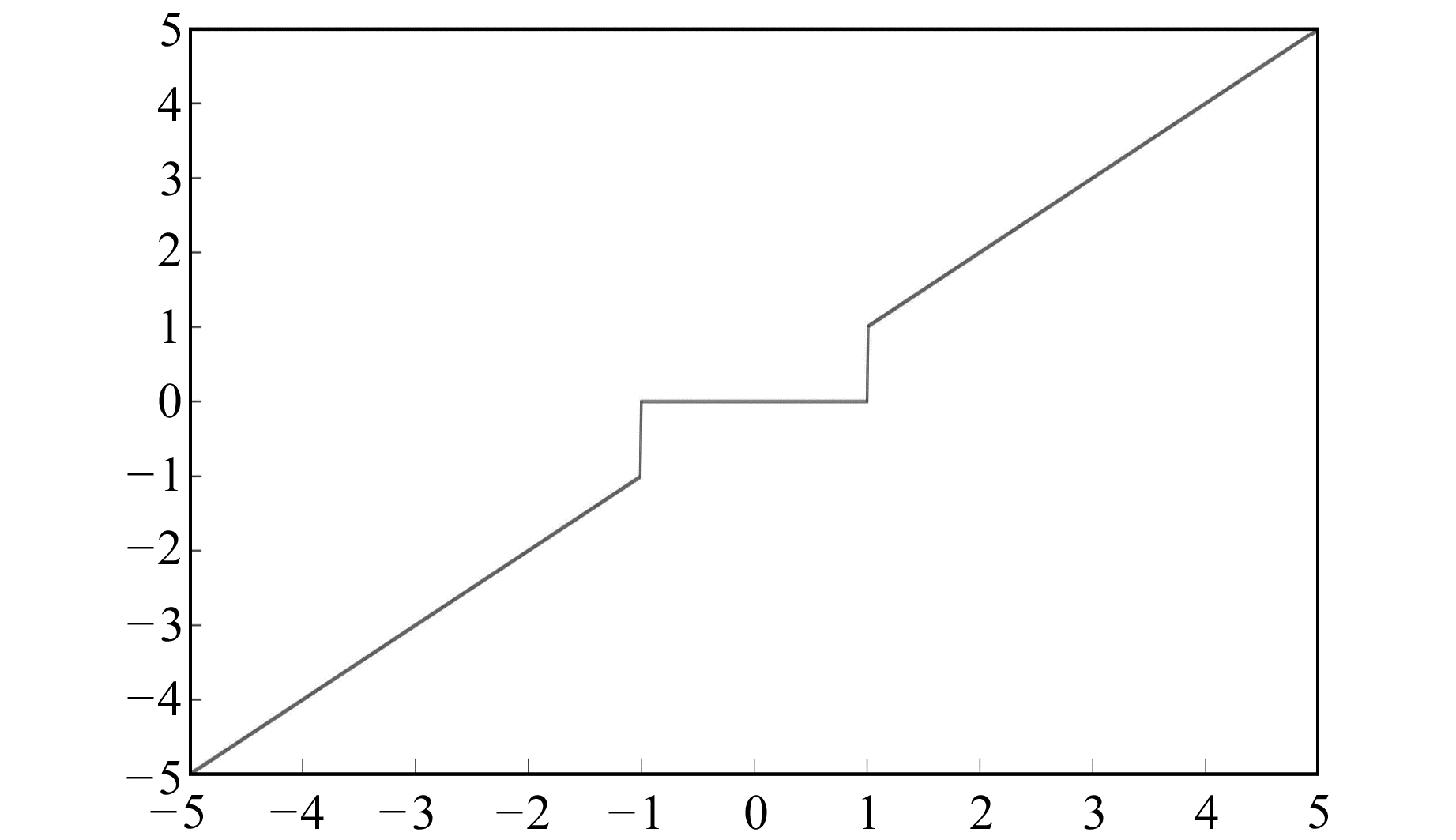
图 1为硬阈值函数图像, 从图中可以看出, 硬阈值函数在阈值±λ处不连续。
|
图 1 硬阈值函数图像 Fig. 1 Function image of hard threshold |
软阈值函数表达式为:
| $ \hat{w}_{j, k}=\left\{\begin{array}{l} 0, \left|w_{j, k}\right|<\lambda \\ \operatorname{sign}\left(w_{j, k}\right)\left|w_{j, k}-T\right|, \left|w_{j, k}\right| \geqslant \lambda \end{array}\right. $ | (6) |
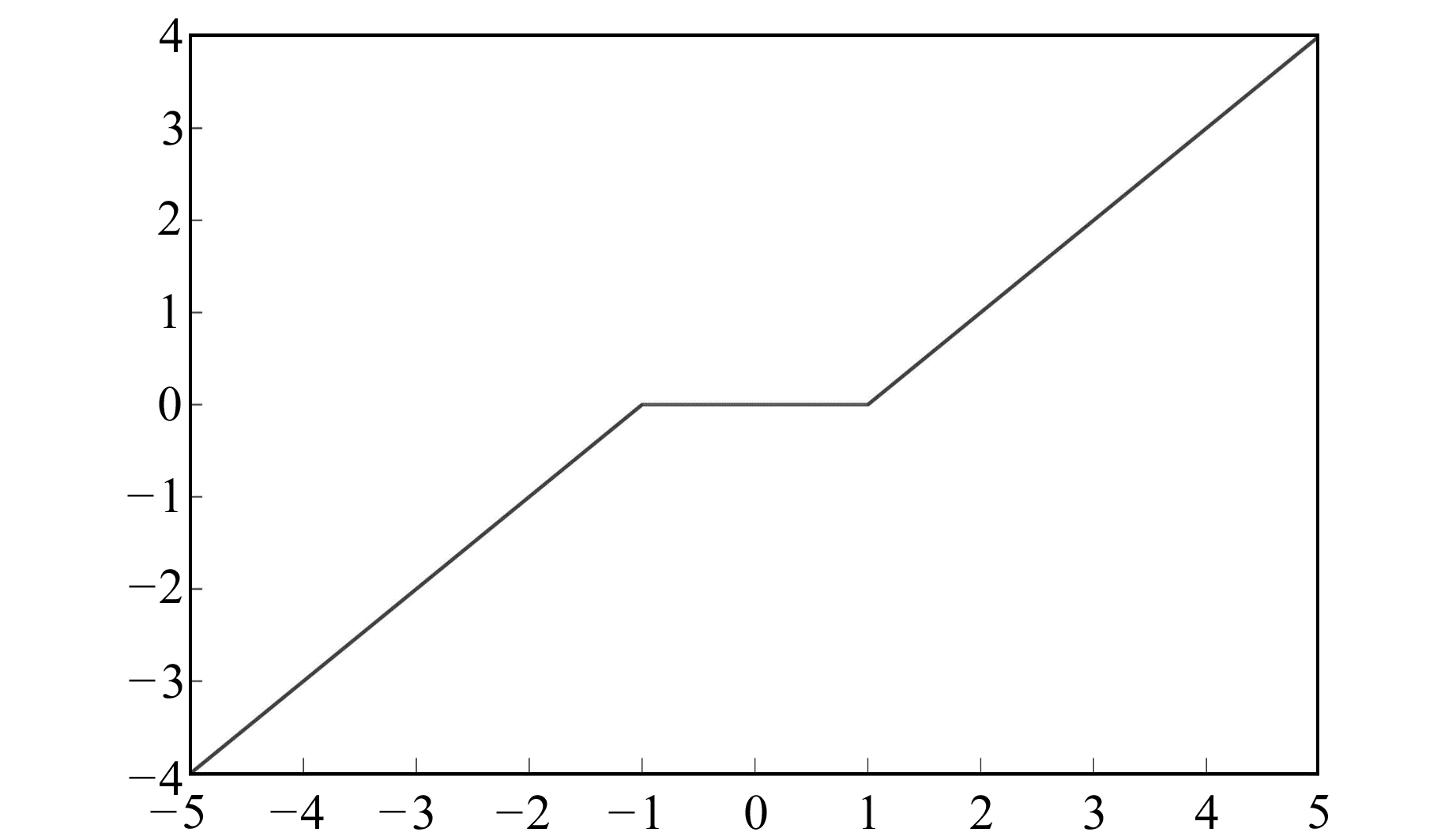
图 2为软阈值函数图像, 从图中可以看出, 软阈值函数可弥补硬阈值函数的缺点, 在阈值±λ处连续, 但存在恒定偏差问题。式(5)~式(6)中, sign为符号函数, wj, k为小波系数,
|
图 2 软阈值函数图像 Fig. 2 Function image of soft threshold |
为弥补传统阈值函数存在的缺点, 本文提出一种改进的阈值函数, 具体表达式为:
| $ f\left(w_{j, k}\right)=\hat{w}_{j, k}=\left\{\begin{array}{l} 0, \left|w_{j, k}\right|<\lambda \\ \frac{2}{\pi} \arctan \left(\left|w_{j, k}\right|-\lambda\right) w_{j, k}+\left(1-\frac{2}{\pi} \arctan \left(\left|w_{j, k}\right|-\lambda\right)\right) \operatorname{sign}\left(w_{j, k}\right) \\ \left(\left|w_{j, k}\right|-\frac{\lambda}{\log _{2}\left(\frac{\left(1+\left|w_{j, k}\right|\right)^{2}-\left(2+\left|w_{j, k}\right|\right) \lambda}{1+\left|w_{j, k}\right|-\lambda}\right)+1}\right), \left|w_{j, k}\right| \geqslant \lambda \end{array}\right. $ | (7) |
本文将从数学方面来分析改进的阈值函数在±λ处的连续性、改进阈值函数的渐近线及克服软阈值函数的恒定偏差。
当wj, k→λ+时,
当wj, k→+∞时,
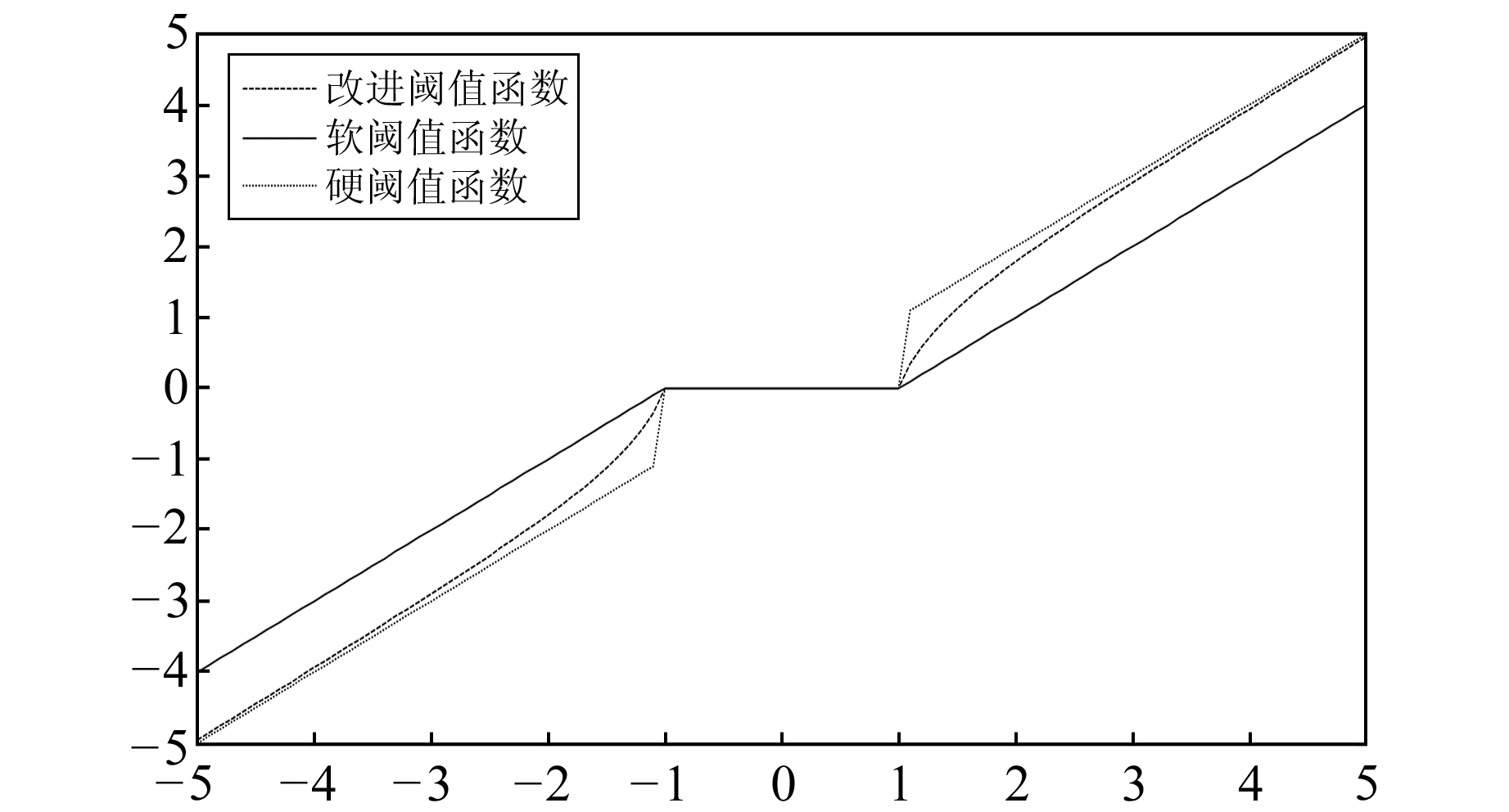
从图 3可以直观看出, 改进的阈值函数可弥补硬阈值函数在阈值±λ处不连续的缺点, 并且在阈值之后能快速趋近硬阈值函数, 从而弥补了软阈值函数存在恒定偏差的缺点。
|
图 3 改进的阈值函数与软硬阈值函数对比 Fig. 3 Comparison of improved threshold function and soft and hard threshold function |
本文选用MATLAB中4种标准测试信号(Blocks, Bumps, Doppler, Heavy sine)分别加入标准偏差为8的高斯白噪声, 再使用本文改进的阈值函数及传统的软、硬阈值函数进行去噪。
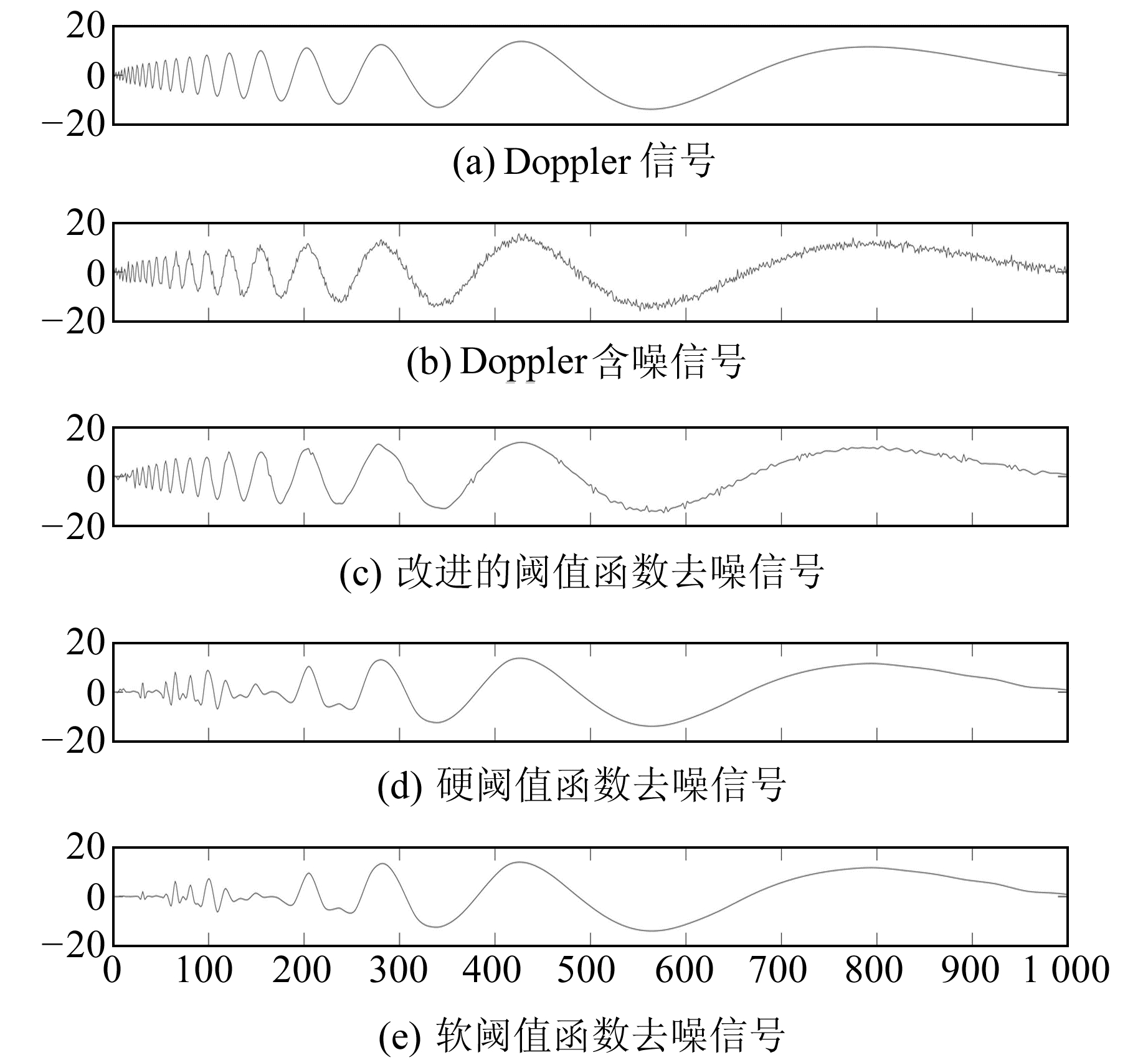
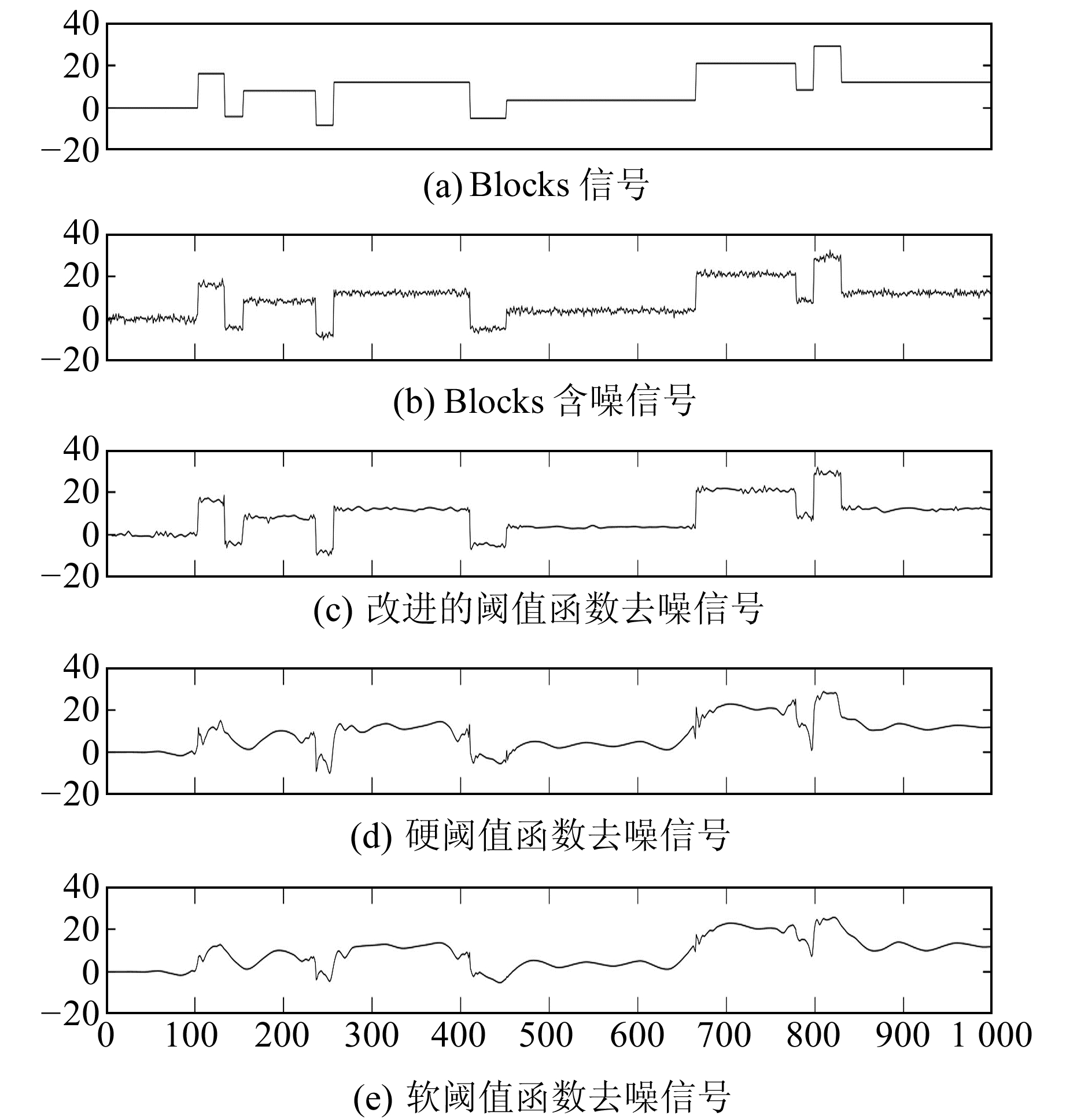
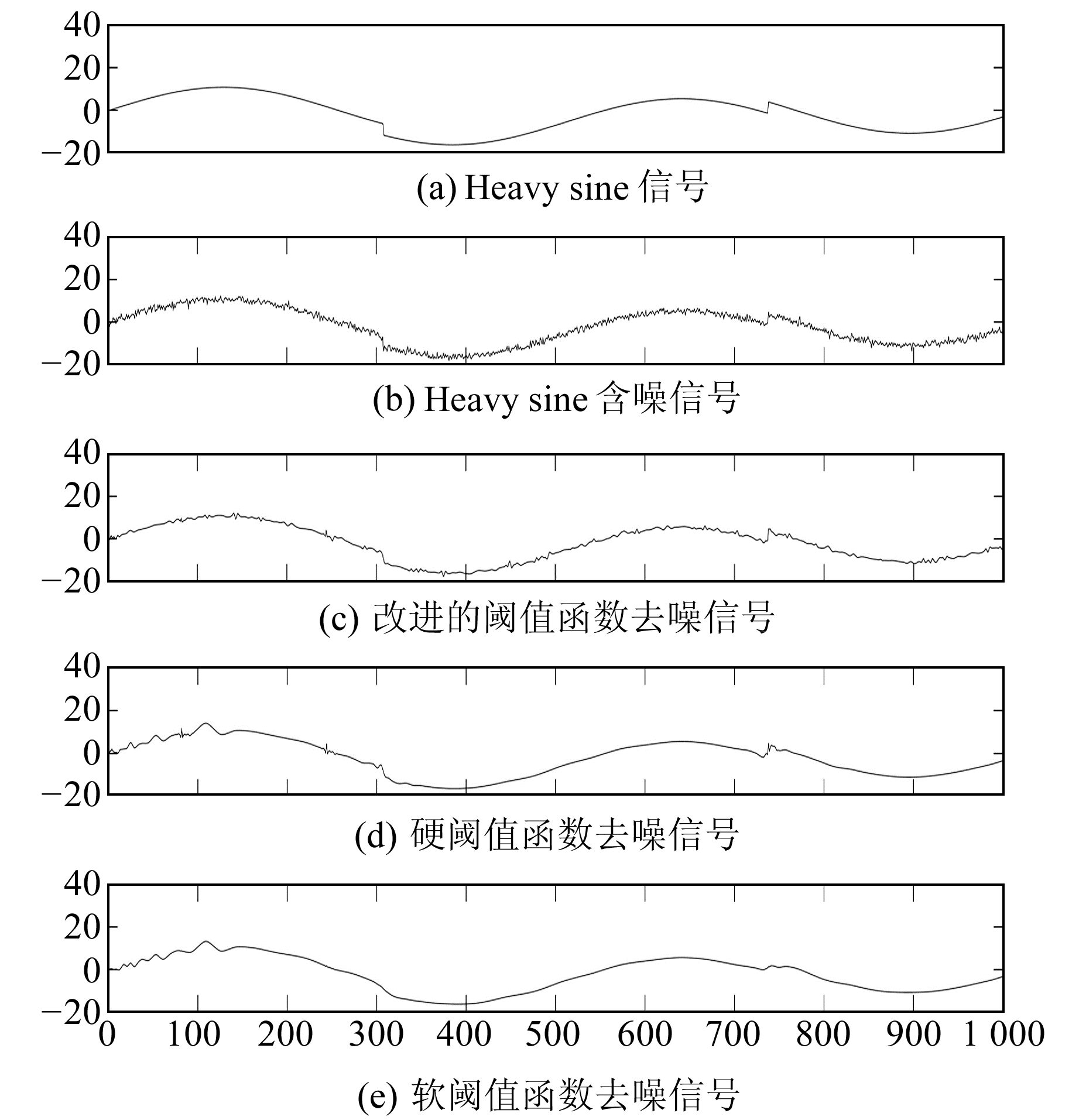
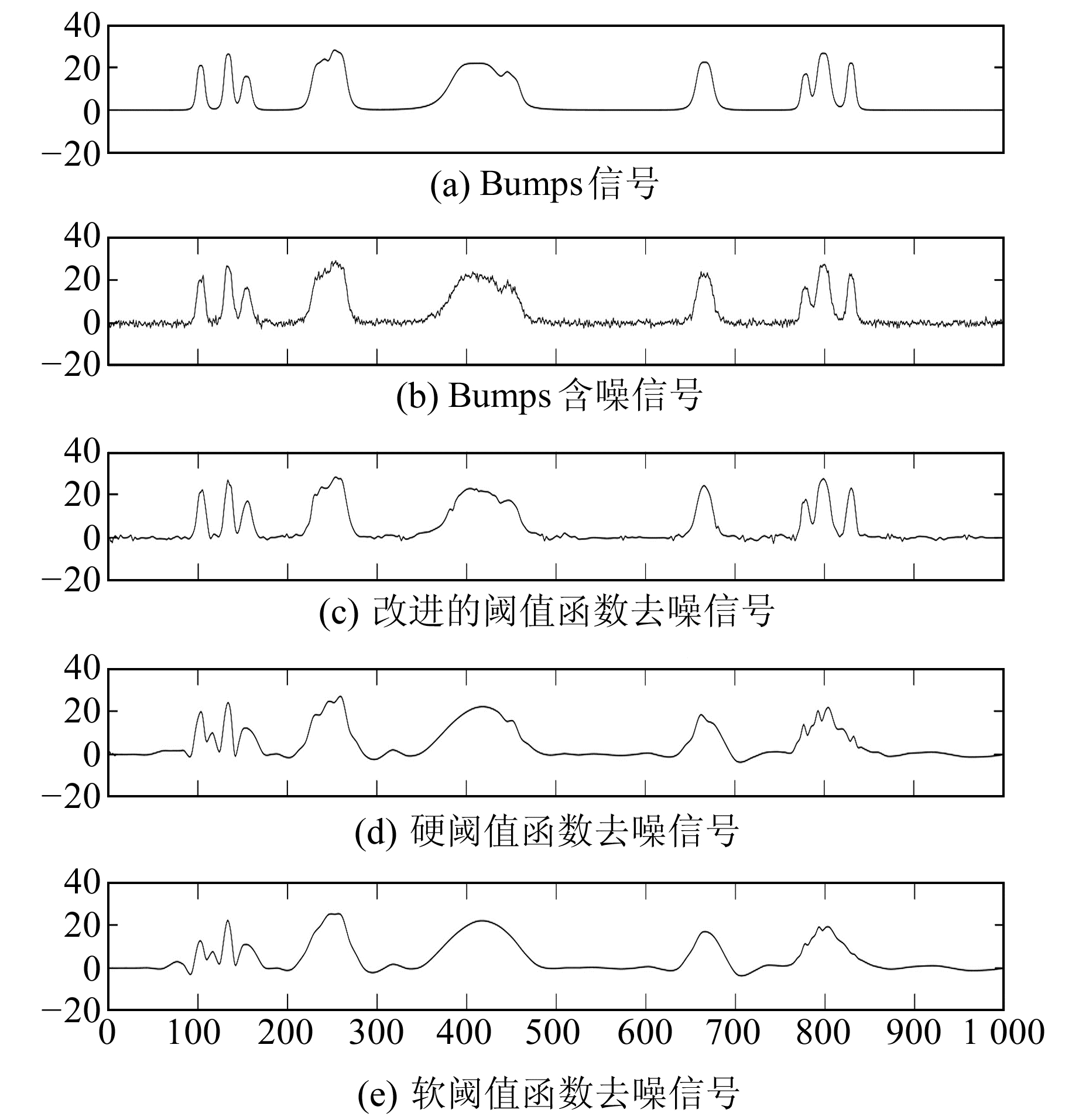
从图 4~7可以看出, 软阈值函数与硬阈值函数去噪均会使原始信号严重失真, 甚至变形。相比于软阈值函数, 硬阈值函数去噪结果存在较多“毛刺”凸起, 这是由硬阈值函数在λ处不连续造成的。相比于硬阈值函数, 虽然软阈值函数可弥补其不连续的缺点, 使得去噪后的信号较为光滑, 但软阈值函数在小波系数大于λ时减去λ, 存在恒定偏差, 从而造成去噪后的结果过于平滑, 影响去噪效果。另外, 改进的阈值函数能在很好地去除高斯白噪声的同时, 改进硬阈值函数的“毛刺”现象及软阈值函数的过度光滑, 使信号不失真。
|
图 4 Doppler信号去噪仿真 Fig. 4 Doppler signal denoising simulation |
|
图 5 Blocks信号去噪仿真 Fig. 5 Blocks signal denoising simulation |
|
图 6 Heavy sine信号去噪仿真 Fig. 6 Heavy sine signal denoising simulation |
|
图 7 Bumps信号去噪仿真 Fig. 7 Bumps signal denoising simulation |
本文将仿真信号的信噪比(SNR)、均方根误差(RMSE)及能量比例(Per)作为去噪后的评价指标:
| $ \mathrm{SNR}=10 \lg \frac{\sum\limits_{i=1}^{n} f^{2}(t)}{\sum\limits_{i=1}^{n}[f(t)-\hat{f}(t)]^{2}} $ | (8) |
| $ \mathrm{RMSE}=\left[\frac{\sum\limits_{i=1}^{n}[f(t)-\hat{f}(t)]^{2}}{n}\right]^{\frac{1}{2}} $ | (9) |
| $ P_{e r}=\frac{\left[\frac{1}{n} \sum\limits_{i=1}^{n} \hat{f}(t)^{2}\right]^{1 / 2}}{\left[\frac{1}{n} \sum\limits_{i=1}^{n} f(t)^{2}\right]^{1 / 2}} $ | (10) |
式(8)~式(10)中, f(t)为原始信号,
在4种信号中加入标准偏差为8的高斯白噪声, 利用控制变量法, 选择提升小波基为bior6.8, 分解与重建尺度为5, 分别使用改进的阈值函数与传统的阈值函数进行去噪处理, 评价指标结果见表 1。通过SNR与RMSE可以看出, 相比于传统的阈值函数, 改进的阈值函数可大大提高去噪后信号的信噪比, 有效去除高斯白噪声, 同时保证仿真信号不失真, 去噪效果明显优于传统方案。从去噪前后的Per可以看出, 改进的阈值函数的提升小波在4种仿真信号中均保持较高比例, 说明相对于软阈值函数与硬阈值函数, 改进的阈值函数可保留较多的原始信号能量成分, 而软阈值函数与硬阈值函数在去噪过程中不仅会去除噪声, 同时也会去除较多的有效信号。
|
|
表 1 仿真信号去噪评价指标 Tab. 1 Evaluation index of simulation signal denoising |
地震波是研究地球结构的有效工具之一[8], 天然地震学与勘探地震学都面临着提高地震资料信噪比的难题[9]。气枪震源是应用于地球内部结构探测的一种新型人工震源[10], 相比于其他人工震源具有可控性好、低频成分丰富、信号重复性高等优点。但气枪震源信号较弱, 受外界噪声干扰较大, 且传播距离有限, 衰减与噪声干扰会使远处台站接收到的气枪信号信噪比极低, 难以分辨。
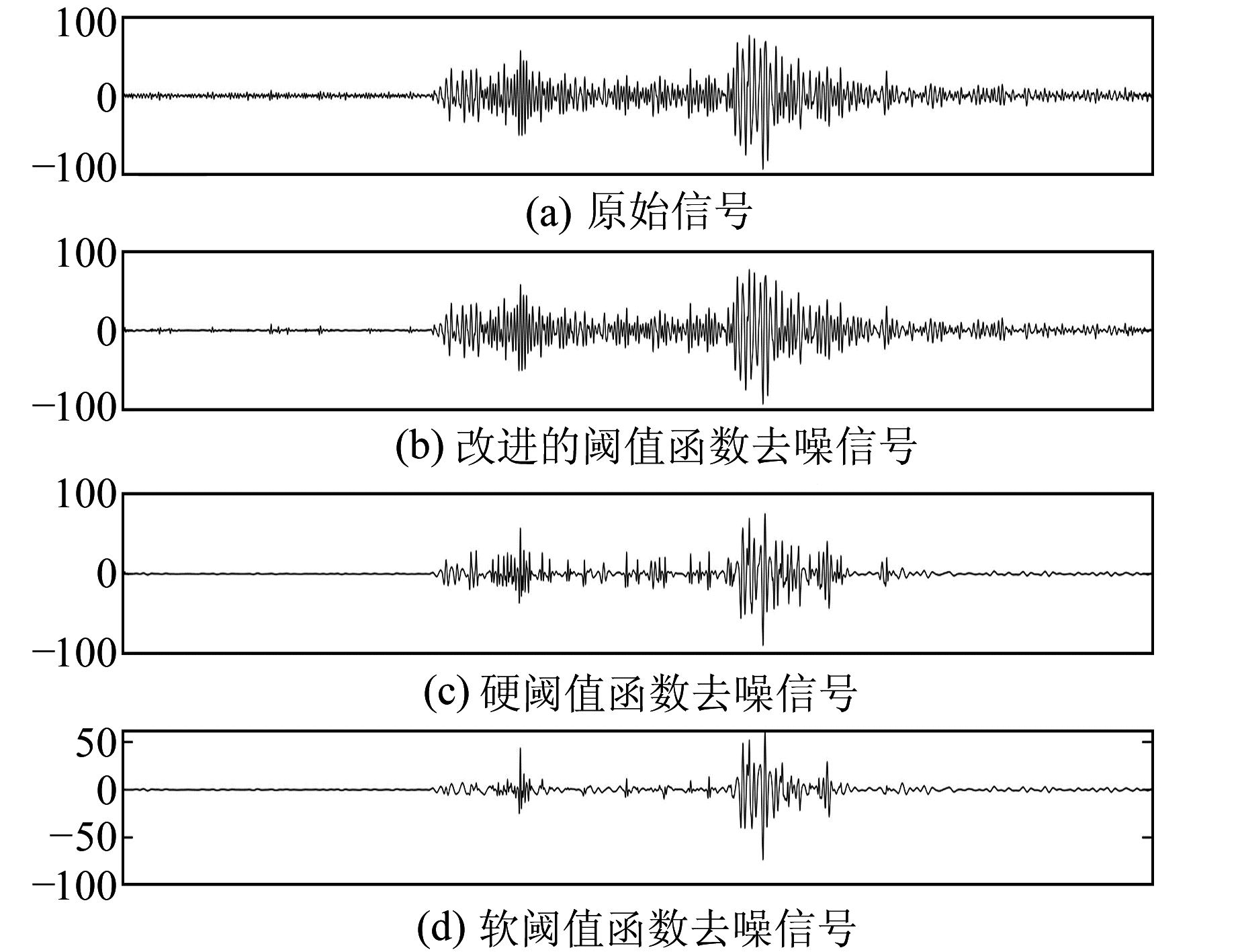
提高气枪信号信噪比的常用方法是利用气枪震源的重复性进行信号叠加[11], 并在此基础上进行带通滤波处理。由于气枪信号的有效信号集中在2~5 Hz之间, 通常使用2~6 Hz的带通滤波处理气枪信号[9], 但该方法存在一定问题, 即不能有效滤除与有效信号具有相同频率的噪声。本文使用云南宾川气枪信号发射台2016年接收到的实验激发数据, 信号接收台站是震中距为151.13 km的53252台站和震中距为115.89 km的53253台站。在叠加气枪信号和进行2~6 Hz带通滤波的基础上对改进阈值函数的提升小波进行去噪处理(图 8~9), 结果表明, 改进的阈值函数不仅可克服传统软、硬阈值函数不连续和存在恒定偏差的缺点, 还可极大地提高气枪震源地震资料的信噪比。

|
图 8 53252台站接收到的信号去噪效果 Fig. 8 Denoising effect of signal received by station 53252 |
|
图 9 53253台站接收到的信号去噪效果 Fig. 9 Denoising effect of signal received by station 53253 |
为直观对比改进的阈值函数的去噪信号与原始信号, 将2个信号进行叠加, 结果见图 10~11。结合图 8~11可以明显看出, 波软阈值函数与硬阈值函数的提升小波在去噪过程中会滤除部分气枪信号的相位信息, 导致有效信号严重失真; 而改进阈值函数的提升小波阈值去噪则在压制噪声的同时几乎未造成有效信息的丢失。上述分析表明, 改进的阈值函数在实际的人工地震信号去噪中比传统的阈值函数表现更优。
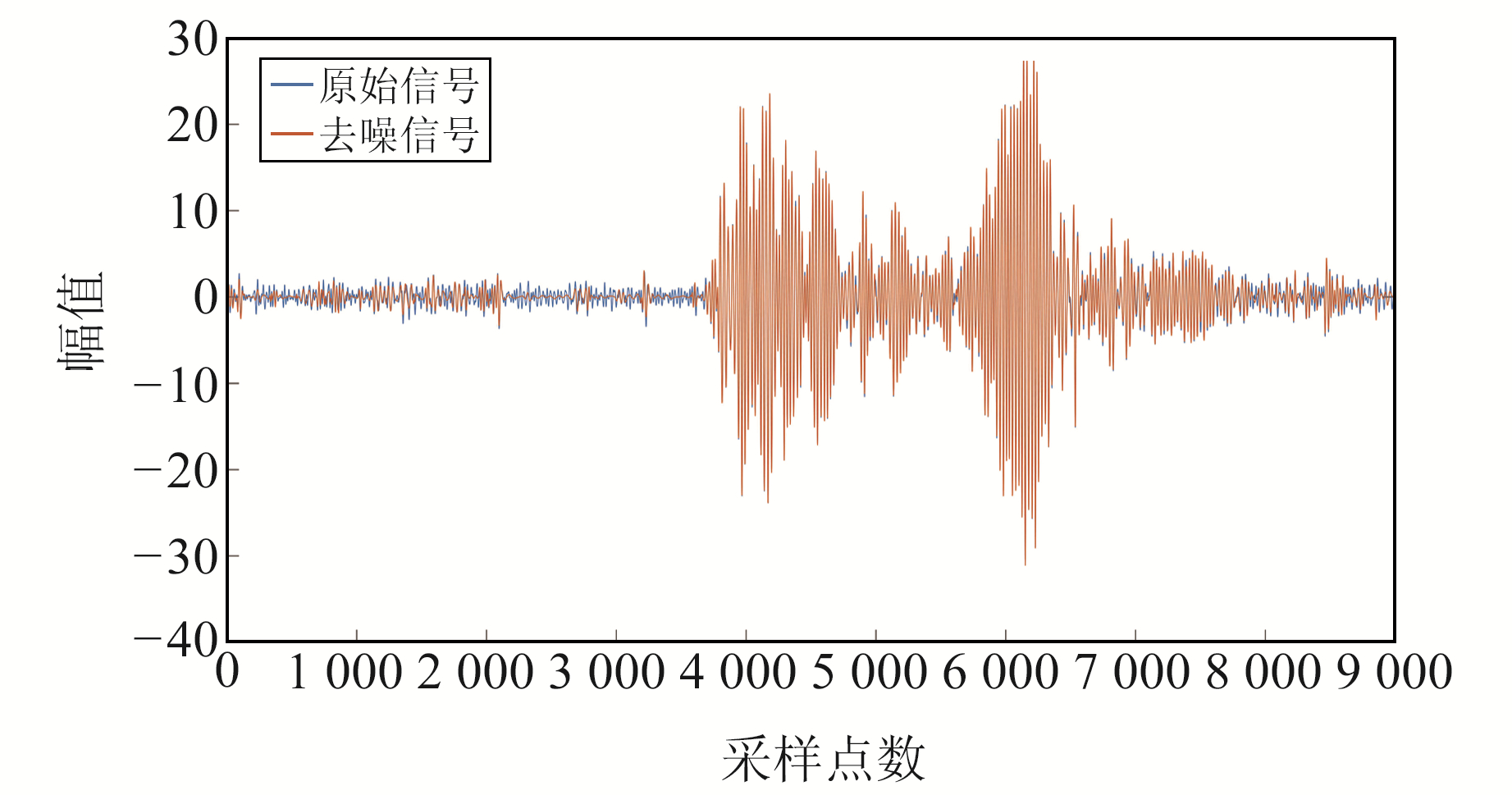
|
图 10 53252台站改进阈值函数去噪信号与原始信号对比 Fig. 10 Comparison of modified threshold function denoising signal and original signal of station 53252 |
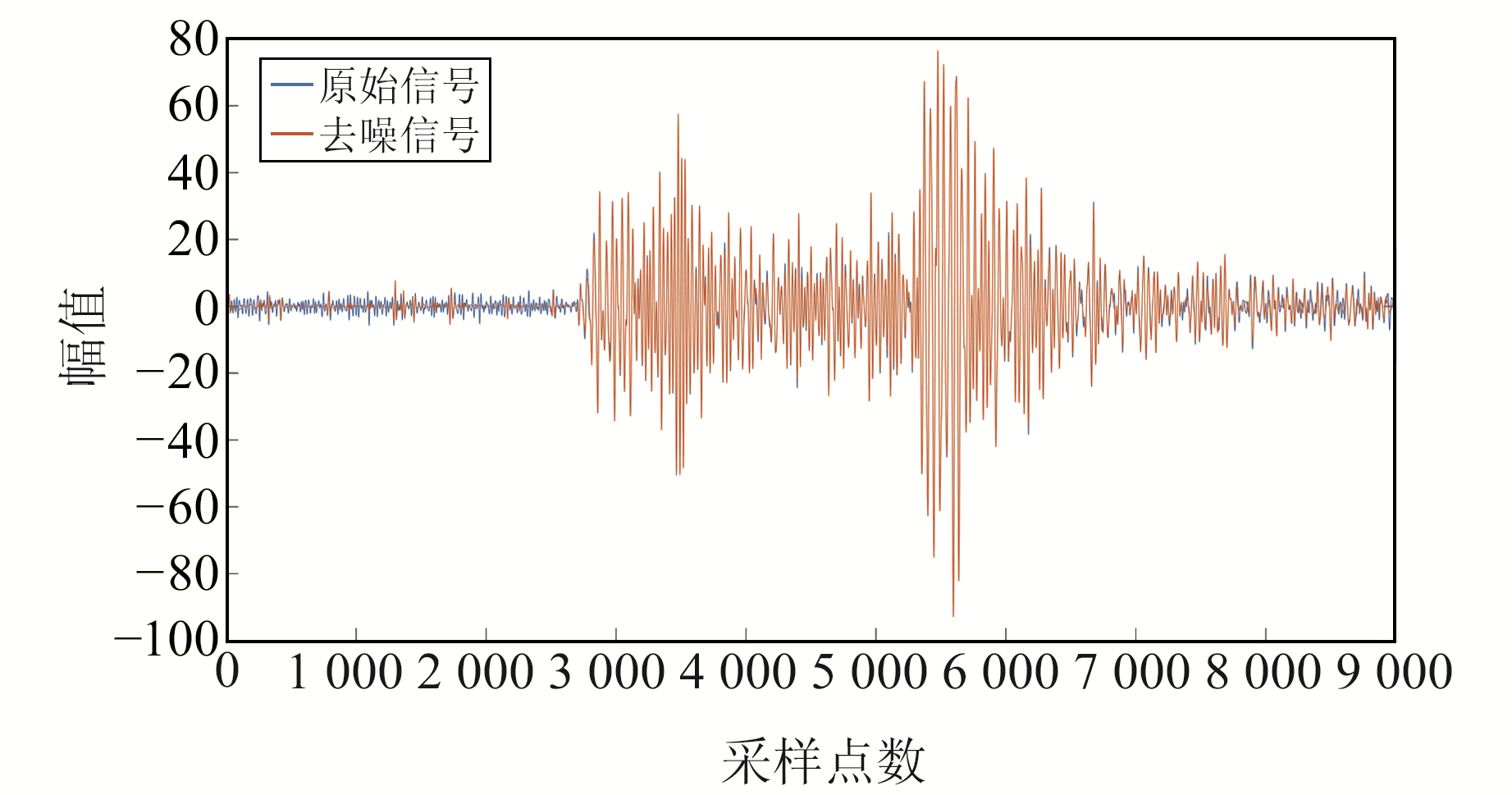
|
图 11 53253台站改进阈值函数去噪信号与原始信号对比 Fig. 11 Comparison of modified threshold function denoising signal and original signal of station 53253 |
从表 2可以看出, 相比于软、硬阈值函数, 改进阈值函数的提升小波在实际的气枪信号去噪中信噪比有大幅提高, 均方根误差减小且能量比例接近1。传统的阈值函数去噪能量比例较小, 表明在去噪过程中传统阈值函数的提升小波会去除许多有效信号, 这与图 8~9的结果相符。分析结果表明, 在实际的气枪震源信号处理中, 改进阈值函数的提升小波算法可克服软阈值函数存在恒定偏差与硬阈值函数不连续的缺点, 提升远处台站气枪震源信号的信噪比是一种可用于气枪震源信号数据处理的有效方法。
|
|
表 2 远处台站信号去噪评价指标 Tab. 2 Evaluation index of signal denoising for distant stations |
图 8~9均为在进行900次气枪信号叠加的基础上通过2~6 Hz带通滤波进行提升小波的阈值去噪处理, 为比较提升小波阈值去噪与带通滤波去噪的效果, 对53253台站接收到的信号进行500次叠加, 并在此基础上分别进行2~6 Hz与2~8 Hz的带通滤波。
从图 12可以看出, 气枪信号在进行叠加后, 改进的阈值函数的提升小波可较好地压制气枪信号的随机噪声, 且未造成气枪信号失真; 而带通滤波虽然可以滤除随机噪声, 但同时也会滤除部分有效信号, 如55~60 s信号, 从而造成一定程度上的信号失真。
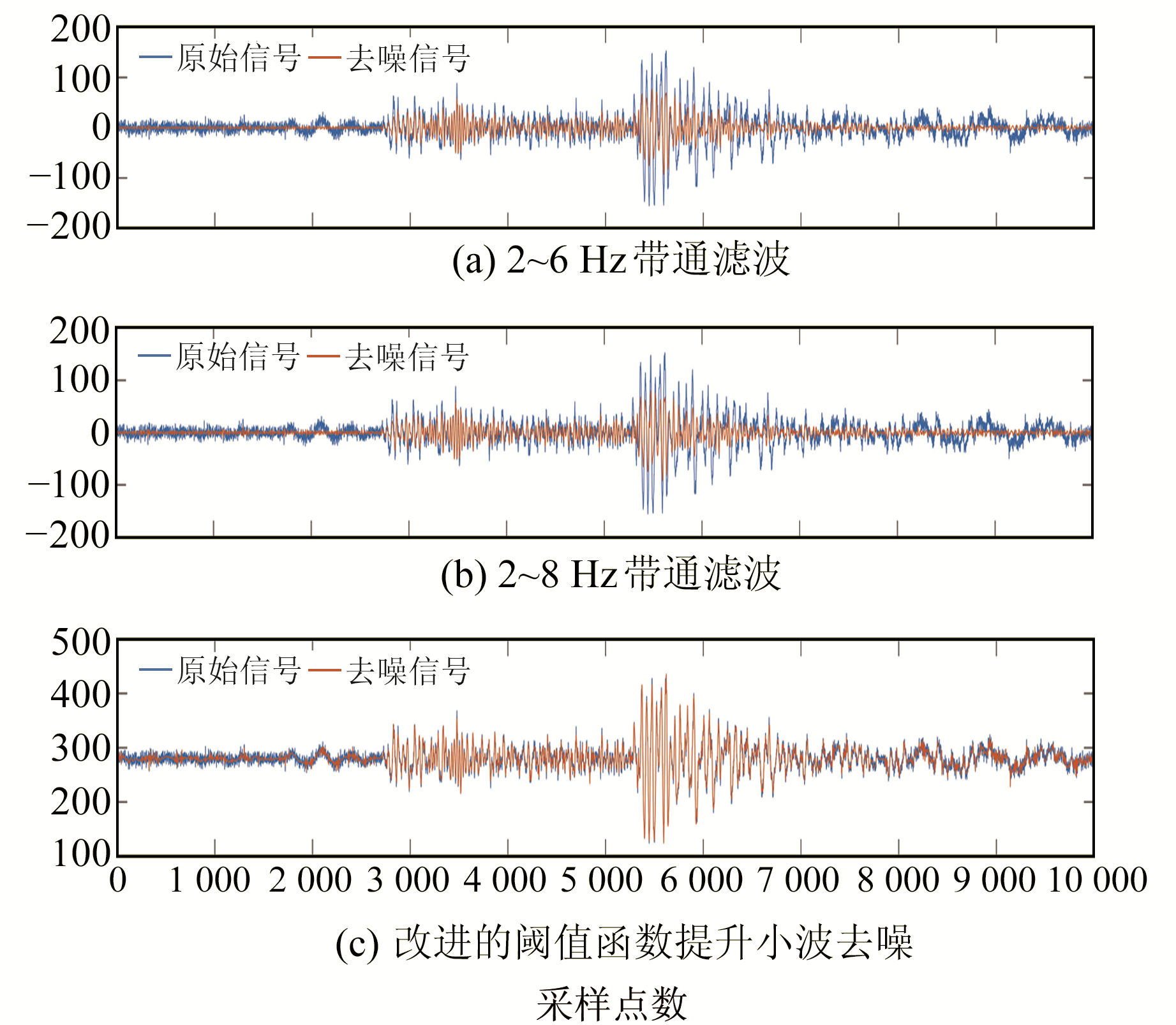
|
图 12 改进阈值函数去噪与带通滤波对比 Fig. 12 Comparison of improved threshold function denoising and bandpass filtering |
本文在传统软、硬阈值函数基础上提出一种新的阈值函数, 并从理论上证明其可在一定程度上弥补软阈值函数存在恒定偏差及硬阈值函数不连续的缺点, 同时将其运用到Blocks、Doppler、Heavy sine和Bumps四种加入高斯白噪声的仿真信号中进行去噪实验。从评价指标SNR和RMSE可以看出, 改进的阈值函数去噪效果优于传统阈值函数, 并且仿真信号不失真。将改进的阈值函数运用到气枪人工震源中发现, 相比于传统阈值函数, 改进的阈值函数能在压制随机噪声并提高远处台站信噪比的同时, 保证有效气枪信号的相位和幅值不失真。将气枪信号进行叠加后发现, 改进的阈值函数在保留有效信号方面优于带通滤波。
致谢: 云南省地震局“主动源创新团队”提供气枪震源数据, 在此表示感谢。
| [1] |
周怀来. 基于小波变换的地震信号去噪方法研究与应用[D]. 成都: 成都理工大学, 2006 (Zhou Huailai. Research and Application of Seismic Signal De-Noising Ways Based on Wavelet[D]. Chengdu: Chengdu University of Technology, 2006)
(  0) 0) |
| [2] |
郑成龙. 基于小波变换的地震信号随机噪声压制[D]. 南昌: 东华理工大学, 2018 (Zheng Chenglong. Noise Suppression of Seismic Signals Based on Wavelet Transform[D]. Nanchang: East China University of Technology, 2018)
(  0) 0) |
| [3] |
覃爱娜, 戴亮, 李飞, 等. 基于改进小波阈值函数的语音增强算法研究[J]. 湖南大学学报: 自然科学版, 2015, 42(4): 136-140 (Qin Aina, Dai Liang, Li Fei, et al. A Speech Enhancement Algorithm Based on Improved Wavelet Threshold Function[J]. Journal of Hunan University(Natural Sciences), 2015, 42(4): 136-140)
(  0) 0) |
| [4] |
王凤利, 赵德有. 基于提升小波和局域波的故障特征提取[J]. 仪器仪表学报, 2010, 31(4): 789-793 (Wang Fengli, Zhao Deyou. Fault Feature Extraction Based on Lifting Wavelet and Local Wave[J]. Chinese Journal of Scientific Instrument, 2010, 31(4): 789-793)
(  0) 0) |
| [5] |
郭迪新, 胡沁春. 基于自适应提升小波的局部放电信号噪声消除[J]. 电机与控制学报, 2006, 10(4): 431-434 (Guo Dixin, Hu Qinchun. Denoising of Partial Discharge Signals Based on Adaptive Lifting Wavelet[J]. Electric Machines and Control, 2006, 10(4): 431-434 DOI:10.3969/j.issn.1007-449X.2006.04.020)
(  0) 0) |
| [6] |
李涛, 何怡刚, 张宇. 基于提升小波的电能质量高效定位算法[J]. 仪器仪表学报, 2013, 34(2): 281-287 (Li Tao, He Yigang, Zhang Yu. High Efficient Location Algorithm for Power Quality Signals with Lifting Wavelet Transform[J]. Chinese Journal of Scientific Instrument, 2013, 34(2): 281-287 DOI:10.3969/j.issn.0254-3087.2013.02.007)
(  0) 0) |
| [7] |
田晓春, 陈家斌, 韩勇强, 等. 一种优化的小波阈值去噪方法在行人导航系统中的应用[J]. 中国惯性技术学报, 2015, 23(4): 442-445 (Tian Xiaochun, Chen Jiabin, Han Yongqiang, et al. Application of Optimized Wavelet Threshold De-Nosing Method in Pedestrian Navigation System[J]. Journal of Chinese Inertial Technology, 2015, 23(4): 442-445)
(  0) 0) |
| [8] |
范小龙, 谢维成, 蒋文波, 等. 一种平稳小波变换改进阈值函数的电能质量扰动信号去噪方法[J]. 电工技术学报, 2016, 31(14): 219-226 (Fan Xiaolong, Xie Weicheng, Jiang Wenbo, et al. An Improved Threshold Function Method for Power Quality Disturbance Signal De-Noising Based on Stationary Wavelet Transform[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 219-226 DOI:10.3969/j.issn.1000-6753.2016.14.025)
(  0) 0) |
| [9] |
陈颙, 王宝善, 姚华建. 大陆地壳结构的气枪震源探测及其应用[J]. 中国科学: 地球科学, 2017, 47(10): 1 153-1 165 (Chen Yong, Wang Baoshan, Yao Huajian. Seismic Airgun Exploration of Continental Crust Structures[J]. Science China: Earth Sciences, 2017, 47(10): 1 153-1 165)
(  0) 0) |
| [10] |
郑成龙. S变换模板滤波及其在主动源数据去噪中的应用研究[D]. 北京: 中国地震局地球物理研究所, 2015 (Zheng Chenglong. Study on Application of S Transform Template Filtering Technology in Active Source Data De-Noising[D]. Beijing: Institute of Geophysics, CEA, 2015)
(  0) 0) |
| [11] |
向涯. 宾川气枪信号特征及利用气枪信号计算宾川地区介质波速变化的研究[D]. 昆明: 云南大学, 2018 (Xiang Ya. Study on Characteristic of Binchuan Air-Gun Signal and the Calculation of Wave Velocity Change in Binchuan Area Using Air-Gun Signal[D]. Kunming: Yunnan University, 2018)
(  0) 0) |
2. National Observation and Research Station for Gavitation and Earth Tide, 40 Hongshance Road, Wuhan 430071, China;
3. Key Laboratory of Earthquake Geodesy, CEA, 40 Hongshance Road, Wuhan 430071, China;
4. Hubei Earthquake Agency, 40 Hongshance Road, Wuhan 430071, China
 2021, Vol. 41
2021, Vol. 41

