2. 中国科学院大学地球与行星科学学院,北京市玉泉路19号甲,100049
随着全球四大导航卫星系统的逐步建成与完善,多系统间的兼容互操作联合定位成为今后GNSS发展的必然趋势[1]。由于不同卫星导航系统间存在系统间偏差(inter-system bias,ISB)和频率不一致等问题,通常使用的多系统相对定位模型为每个系统独立选择参考星,形成系统内双差,这种组合方式一般称为松组合。而紧组合是指不同系统间只选择一颗参考星,既形成了系统内双差,又形成了系统间双差[2-3]。在一些复杂观测环境(如树下、城市峡谷等),由于卫星数量严重缺失,此时使用单系统解算模式可能出现无法解算的情况,而使用双系统联合定位模式仍可以解算。另外,在卫星数量十分稀少的情况下,松组合模型很难固定模糊度,而紧组合模型能有效增加观测方程数量,提高模糊度固定率及定位精度。
目前,国内外学者对紧组合的研究主要集中在GPS/Galileo组合的重叠频率(L1与E1)上,而对BDS与其他系统间的紧组合及不同系统间非重叠频率紧组合的研究较少[4-11]。本文对短基线下GPS-L1(1 575.42 MHz)/BDS-B1(1 561.098 MHz) 非重叠频率紧组合相对定位算法进行研究,详细推导了短基线下GPS-L1/BDS-B1非重叠频率紧组合相对定位数学模型,并对事先标定DISB的方法进行详细介绍; 同时,分析GPS-L1/BDS-B1非重叠频率DISB的稳定性,并基于GPS-L1/BDS-B1单历元相对定位实验验证紧组合相较于松组合的优越性。
1 数学模型由于GPS和BDS使用的坐标系统及时间系统不一致,在进行GPS/BDS精密相对定位时必须进行考虑。在坐标系统方面,尽管GPS和BDS分别采用WGS-84和CGCS2000坐标系,但在进行相对定位时,两者的区别可以忽略不计[12-13]; 在时间系统方面,GPS时与BDS时相差14 s,因此将BDS时加上14 s,使两者的时间系统统一[14]。
1.1 非差观测方程假设一台GNSS接收机同时接收GPS/BDS伪距与载波相位观测值,则卫星s与接收机i之间的非差伪距与载波相位观测方程为:
| $ P_{\mathrm{i}}^{\mathrm{s}}=\rho_{\mathrm{i}}^{\mathrm{s}}+\mathrm{d} t_{\mathrm{i}}-\mathrm{d} t^{\mathrm{s}}+d_{\mathrm{i}}-d^{\mathrm{s}}+T_{\mathrm{i}}^{\mathrm{s}}-I_{\mathrm{i}}^{\mathrm{s}}+e_{\mathrm{i}}^{\mathrm{s}} $ | (1) |
| $ \begin{array}{c} \varphi_{\mathrm{i}}^{\mathrm{s}}=\rho_{\mathrm{i}}^{\mathrm{s}}+\mathrm{d} t_{\mathrm{i}}-\mathrm{d} t^{\mathrm{s}}+\lambda\left(\varPhi_{\mathrm{i}}-\varPhi^{\mathrm{s}}+\delta_{\mathrm{i}}-\right. \\ \left.\delta^{\mathrm{s}}+N_{\mathrm{i}}^{\mathrm{s}}\right)+T_{\mathrm{i}}^{\mathrm{s}}-I_{\mathrm{i}}^{\mathrm{s}}+\varepsilon_{\mathrm{i}}^{\mathrm{s}} \end{array} $ | (2) |
式中,Pis、φis分别为卫星s与接收机i之间伪距和载波相位的观测值(单位m); ρis为卫星s与接收机i之间的几何距离; dti为接收机钟差; dts为卫星钟差; di为接收机端的伪距硬件延迟; ds为卫星端的伪距硬件延迟; Tis为对流层延迟; Iis为电离层延迟; eis为伪距测量噪声; λ为波长; Φi为接收机端的初始相位; Φs为卫星端的初始相位; δi为接收机端硬件延迟; δs为卫星端硬件延迟; Nis为整周模糊度; εis为相位测量噪声。
1.2 单差观测方程在测站i、j之间作差可以消除与卫星有关的误差。在短基线情况下,可以忽略电离层和对流层延迟,用单差算子Δ表示观测值之差,则i、j站间的单差观测方程可表示为:
| $ \Delta P_{i j}^{\mathrm{s}}=\Delta \rho_{i j}^{\mathrm{s}}+\Delta \mathrm{d} t_{i j}+\Delta d_{i j}+\Delta e $ | (3) |
| $ \begin{array}{c} \Delta \varphi_{i j}^{\mathrm{s}}=\Delta \rho_{i j}^{\mathrm{s}}+\Delta \mathrm{d} t_{i j}+ \\ \lambda\left(\Delta \varPhi_{i j}+\Delta \delta_{i j}+\Delta N_{i j}^{\mathrm{s}}\right)+\Delta \varepsilon \end{array} $ | (4) |
GPS/BDS松组合联合相对定位解算时,假设GPS/BDS系统分别选择G1、B1作为参考星,系统内双差可以进一步消除与接收机相关的误差,用双差算子Δ
| $ \Delta \nabla P_{i j}^{\mathrm{G} 1 \mathrm{G} i}=\Delta \nabla \rho_{i j}^{\mathrm{G} 1 \mathrm{G} i}+\Delta \nabla e $ | (5) |
| $ \Delta \nabla \varphi_{i j}^{\mathrm{G} 1 \mathrm{G} i}=\Delta \nabla \rho_{i j}^{\mathrm{G} 1 \mathrm{G} i}+\lambda_{\mathrm{L} 1} \Delta \nabla N_{i j}^{\mathrm{G} 1 \mathrm{G} i}+\Delta \nabla \varepsilon $ | (6) |
| $ \Delta \nabla P_{i j}^{\mathrm{C1C} i}=\Delta \nabla \rho_{i j}^{\mathrm{C1C} i}+\Delta \nabla e $ | (7) |
| $ \Delta \nabla \varphi_{i j}^{\mathrm{C} 1 \mathrm{C} i}=\Delta \nabla \rho_{i j}^{\mathrm{C} 1 \mathrm{C} i}+\lambda_{\mathrm{B} 1} \Delta \nabla N_{i j}^{\mathrm{C1C} i}+\Delta \nabla \varepsilon $ | (8) |
式中,G代表GPS系统,C代表北斗系统; Δ
在松组合模型中,每个系统选择各自的参考星进行系统内双差; 而在紧组合模型中,多个系统选择一个共同的参考星,除系统内双差外,还需进行系统间双差。假设GPS/BDS紧组合定位时,选择G1作为双系统的共同参考星,则双差方程可表示为:
| $ \Delta \nabla P_{i j}^{\mathrm{G} 1 \mathrm{C} i}=\Delta \nabla \rho_{i j}^{\mathrm{G} 1 \mathrm{C} i}+\Delta d_{i j}^{\mathrm{C}}-\Delta d_{i j}^{\mathrm{G}}+\Delta \nabla e $ | (9) |
| $ \begin{array}{c} \Delta \nabla \varphi_{i j}^{\mathrm{G} 1 \mathrm{C} i}=\Delta \nabla \rho_{i j}^{\mathrm{G} 1 \mathrm{C} i}+\left(\lambda_{\mathrm{B} 1} \Delta \varPhi_{i j}-\lambda_{\mathrm{L} 1} \Delta \varPhi_{i j}\right)+ \\ \left(\lambda_{\mathrm{B} 1} \Delta \delta_{i j}^{\mathrm{C}}-\lambda_{\mathrm{L} 1} \Delta \delta_{i j}^{\mathrm{G}}\right)+\lambda_{\mathrm{B} 1} \Delta N_{i j}^{\mathrm{C}}-\lambda_{\mathrm{L} 1} \Delta N_{i j}^{\mathrm{G}}+\Delta \nabla \varepsilon \end{array} $ | (10) |
由于GPS-L1和BDS-B1的频率不一致,进行系统间双差时接收机端初始相位无法消除,单差硬件延迟无法形成双差硬件延迟,单差模糊度也无法形成双差模糊度,此时进行参数重组,令
| $ \Delta d_{i j}^{\mathrm{C}}-\Delta d_{i j}^{\mathrm{G}}=\mathrm{PDISB} $ | (11) |
| $ \begin{array}{*{20}{c}} {\left( {{\lambda _{{\rm{B}}1}}\Delta {\mathit{\Phi }_{ij}} - {\lambda _{{\rm{L}}1}}\Delta {\mathit{\Phi }_{ij}}} \right) + \left( {{\lambda _{{\rm{B}}1}}\Delta \delta _{ij}^{\rm{C}} - {\lambda _{{\rm{L}}1}}\Delta \delta _{ij}^{\rm{G}}} \right) = }\\ {{\lambda _{{\rm{B}}1}}{\rm{DISB}}} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {{\lambda _{{\rm{B}}1}}\Delta N_{ij}^{\rm{C}} - {\lambda _{{\rm{L}}1}}\Delta N_{ij}^{\rm{G}} = {\lambda _{{\rm{B}}1}}\Delta N_{ij}^{\rm{C}} - {\lambda _{{\rm{B}}1}}\Delta N_{ij}^{\rm{G}} + }\\ {{\lambda _{{\rm{B}}1}}\Delta N_{ij}^{\rm{G}} - {\lambda _{{\rm{L}}1}}\Delta N_{ij}^{\rm{G}} = {\lambda _{{\rm{B}}1}}\Delta \nabla N_{ij}^{{\rm{GC}}} + \left( {{\lambda _{{\rm{BIL}}1}}} \right)\Delta N_{ij}^{\rm{G}}} \end{array} $ | (13) |
与重叠频率紧组合的DISB相比,式(12)将单差初始相位之差与单差硬件延迟之差整合为DISB参数,非重叠频率的DISB增加了单差初始相位之差; 式(13)将单差模糊度之差转换为双差模糊度与单差模糊度之和,其中ΔNijG可由GPS的单差伪距近似计算得到,一般可精确到3周,因(λB1-λL1)约为0.001 7 m,故(λB1L1)ΔNijG的精度约为3 mm,满足精度要求,不会对双差模糊度的固定产生影响[15]。
由于紧组合模型多估计了一个DISB参数,导致法方程秩亏,并且单频时秩亏数为1,此时要对参数进行重组,令
| $ \begin{array}{c} \Delta \nabla N_{i j}^{\mathrm{G1C}i}=\Delta N_{i j}^{\mathrm{G} 1}-\Delta N_{i j}^{\mathrm{C} 1}+\Delta N_{i j}^{\mathrm{C1}}-\Delta N_{i j}^{\mathrm{C} i}= \\ \Delta \nabla N_{i j}^{\mathrm{G} 1 \mathrm{C} 1}+\Delta \nabla N_{i j}^{\mathrm{C1C} i} \end{array} $ | (14) |
| $ \widetilde{\mathrm{DISB}}=\mathrm{DISB}+\Delta \nabla N_{i j}^{\mathrm{G1C1}} $ | (15) |
式(14)将BDS卫星Ci与GPS参考星G1的双差模糊度转换为C1、G1的双差模糊度与C1、Ci的双差模糊度之和,其中C1卫星为BDS系统内部参考星。式(15)将DISB参数与C1、G1的双差模糊度参数整合为
| $ \Delta \nabla P_{i j}^{\mathrm{G1C} i}=\Delta \nabla \rho_{i j}^{\mathrm{G} 1 \mathrm{C} i}+\mathrm{PDISB}+\Delta \nabla e $ | (16) |
| $ \begin{array}{c} \Delta \nabla \widetilde{\varphi}_{i j}^{\mathrm{G1C} i}=\Delta \nabla \varphi_{i j}^{\mathrm{G} 1 \mathrm{C} i}-\lambda_{\mathrm{B} 1 \mathrm{L} 1} \Delta N_{i j}^{\mathrm{G}}= \\ \Delta \nabla \rho_{i j}^{\mathrm{G} 1 \mathrm{C} i}+\lambda_{\mathrm{B} 1} \widetilde{\mathrm{~DISB}}+\lambda_{\mathrm{B} 1} \Delta \nabla N_{i j}^{\mathrm{C1C} i}+\Delta \nabla \varepsilon \end{array} $ | (17) |
虽然紧组合模型增加了观测方程数量,但同时也增加了待估参数,方程的冗余度不变,所以理论上模型强度不变,并不会增加定位的精度和模糊度固定的成功率[6-8]。
1.5 事先标定DISB通过式(16)和式(17)计算出
| $ \widetilde{P}_{i j}^{\mathrm{G} 1 \mathrm{C} i}=P_{i j}^{\mathrm{G} 1 \mathrm{Ci}}-\mathrm{PDISB}=\rho_{i j}^{\mathrm{G} 1 \mathrm{C} i}+e_{i j}^{\mathrm{G1C} i} $ | (18) |
| $ \begin{aligned} \Delta \nabla \tilde{\varphi}_{i j}^{\mathrm{G1C} i} &=\Delta \nabla \varphi_{i j}^{\mathrm{G} 1 \mathrm{C} i}-\lambda_{\mathrm{B} 1 \mathrm{L} 1} \Delta N_{i j}^{\mathrm{G}}-\lambda_{\mathrm{B} 1} \widetilde{\mathrm{~DISB}}=\\ & \Delta \nabla \rho_{i j}^{\mathrm{G} 1 \mathrm{C} i}+\lambda_{\mathrm{B} 1} \Delta \nabla N_{i j}^{\mathrm{C1C} i}+\Delta \nabla \varepsilon \end{aligned} $ | (19) |
由式(15)可知,采用紧组合相对定位模型估计出的DISB参数实际上吸收了参考星之间的双差模糊度,即使采用单历元模式进行解算,仍需考虑参考星的变换。在对最开始参考星不变的几个历元进行DISB标定后,如果参考星发生变化,可以采用式(20)对标定的DISB进行转换:
| $ \begin{array}{l} \widetilde{\mathrm{DISB}}_{i}=\mathrm{DISB}_{i}+\Delta \nabla N_{i j}^{\mathrm{G}m\mathrm{C}n}= \\ \widetilde{\mathrm{DISB}}_{i-1}-\Delta \nabla N_{i j}^{\mathrm{G1G} m}+\Delta \nabla N_{i j}^{\mathrm{C1} \mathrm{C} n} \end{array} $ | (20) |
式中,
本文选取科廷大学短基线实验数据(CUTB0~CUTC0),其中2台接收机类型相同,均选用Trimble NetR9接收机,天线类型为TRM 59800.00 SCIS,数据采集时间为2018-01-08,采样间隔为30 s。数据处理策略为GPS-L1/BDS-B1单历元短基线相对定位,利用高度角定权方法,选取高度角最大的卫星作为参考星,固定模糊度采用最小二乘模糊度降相关平差法(LAMBDA),并根据ratio值是否达到阈值3或5对模糊度是否固定成功进行判断[10]。
分别采用松组合与事先标定DISB的紧组合模型对实验数据进行处理,并对处理结果进行比较分析。首先使用紧组合相对定位模型对DISB的稳定性进行分析,并对事先标定DISB的方法进行详细介绍,分别对截止高度角为10°、20°、30°、40°时2种数据处理模式的模糊度固定率及误差分布进行统计与分析。
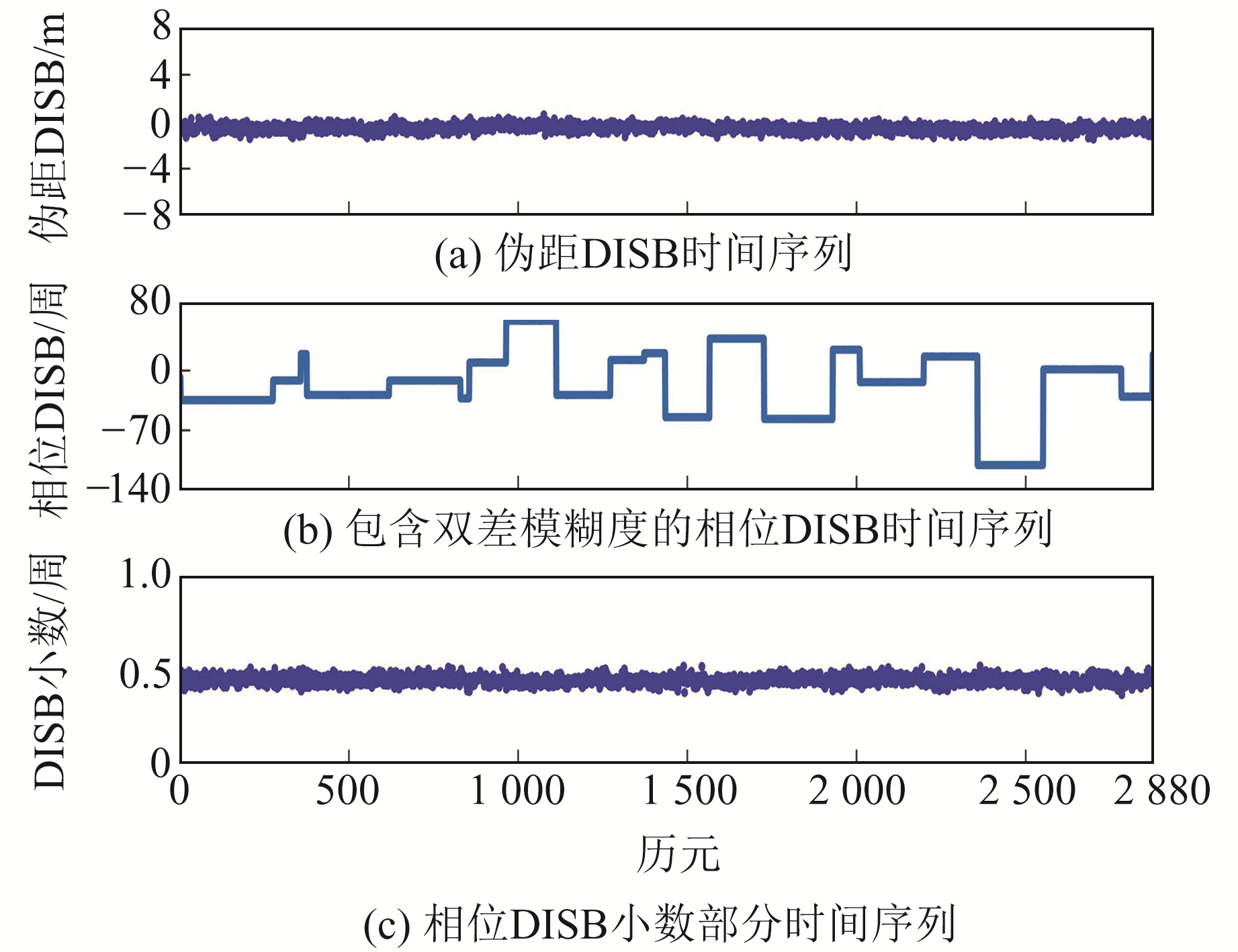
2.2 DISB稳定性分析采用式(16)和式(17)的紧组合相对定位模型对实验数据进行解算,得到伪距DISB及相位DISB的估值时间序列,结果如图 1(a)和1(b)所示。从图 1(a)可以看出,解算得到的伪距DISB值十分稳定,平均值为-0.54 m,标准差为0.28 m,由式(15)可知,采用紧组合相对定位模型估计出的DISB参数实际上吸收了参考星之间的双差模糊度。从图 1(b)可以看出,每次参考星变换都会引起DISB估值的变化,而在参考星稳定不变的时间域内,所估得的DISB值也十分稳定。由于参考星之间的双差模糊度参数与相位DISB参数系数相同,无法将实际的相位DISB单独分离出来,故在分析相位DISB稳定性时,通常只分析所估计出的DISB参数的小数部分,整数部分被参考星间双差模糊度吸收。图 1(c)为采用式(16)和式(17)估计出的DISB参数的小数部分,从图中可以看出,其在时间域内十分稳定,平均值为0.44周,标准差为0.02周。由此可知,可以采用事先标定DISB的紧组合模型对实验数据进行解算。
|
图 1 伪距与相位DISB时间序列 Fig. 1 DISB time series of pseudo range and phase |
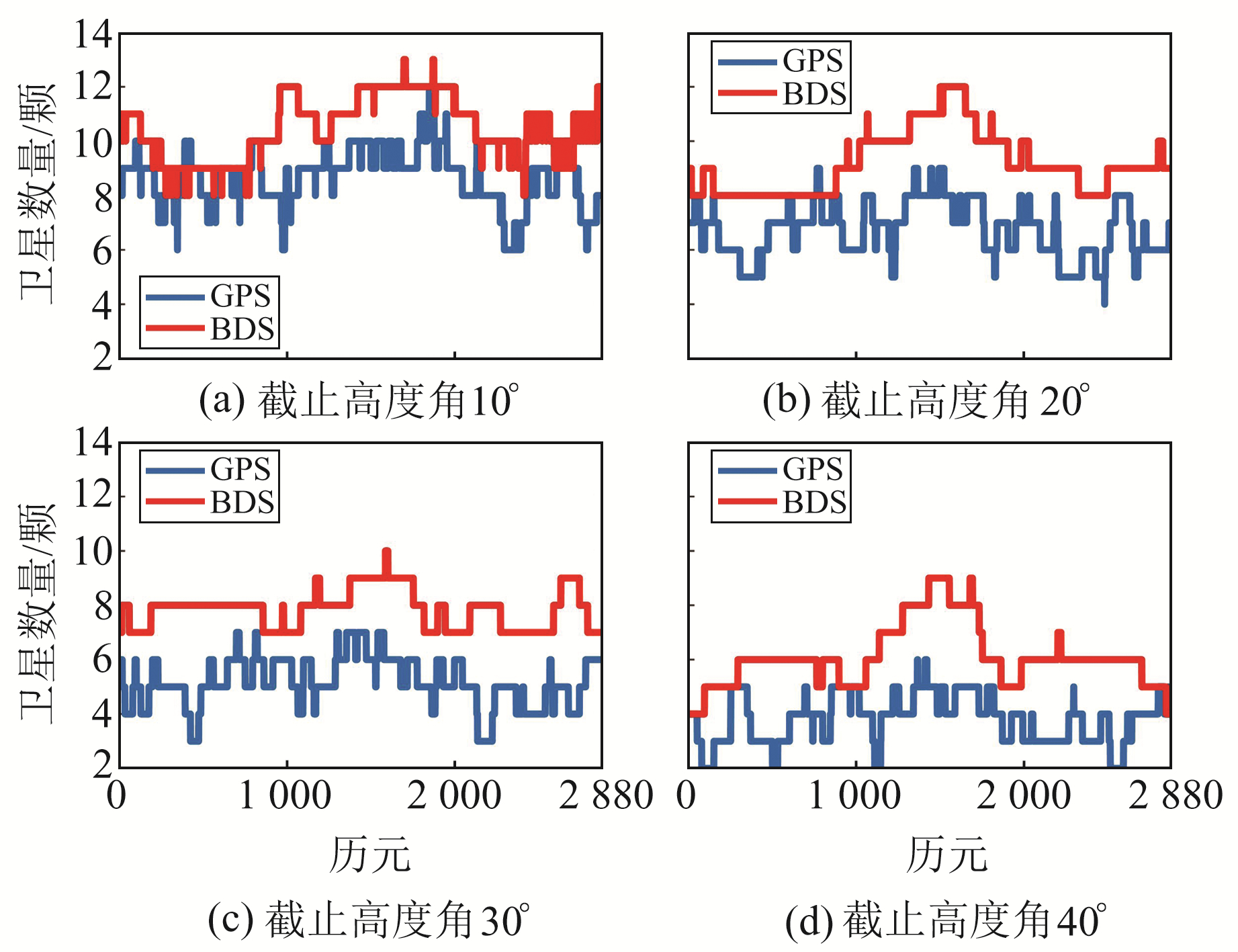
对截止高度角为10°、20°、30°、40°时GPS/BDS的可观测卫星数量进行统计,结果见图 2。从图中可以看出,当截止高度角为10°和20°时,GPS/BDS每个历元的卫星数量都在4颗以上; 当截止高度角为30°时,BDS系统卫星数量都还在4颗以上,而GPS系统则出现少量卫星数为3颗的历元,此时使用GPS单系统解算模式将无法解算; 当卫星高度角为40°时,BDS系统的卫星数量仍然保持在4颗以上,GPS系统则出现了大量卫星数量在4颗以下的历元,此时使用GPS单系统解算模式将出现大量无法解算的历元,使用双系统联合定位模式仍可以解算。
|
图 2 不同截止高度角卫星数量 Fig. 2 Figure of the number of satellites with different cut-off altitudes |
图 3为不同截止高度角下GPS-L1/BDS-B1松组合与事先标定紧组合的模糊度固定ratio值,从图中可以看出,当截止高度角为10°时,紧组合与松组合的模糊度固定ratio值整体相差不大,这是因为卫星数量充足,紧组合相对松组合对ratio值的提高还不是十分明显,此时松组合的平均ratio值为10.0,紧组合的平均ratio值为12.5。当截止高度角为20°和30°时,紧组合的ratio值已经明显高于松组合,这是因为随着卫星数量的减少,紧组合模型增加的多余观测量产生的效果越来越明显。高度角为20°时松组合的平均ratio值为13.7,紧组合的平均ratio值为25.9;高度角为30°时松组合的平均ratio值为10.5,紧组合的平均ratio值为29.1。当高度角为40°时,紧组合的一部分历元远远高于松组合,主要因为此时卫星数量十分稀少,GPS系统大部分历元卫星数在4颗以下,使用松组合很难固定模糊度,而紧组合在这种场景下具有巨大优势,此时松组合的平均ratio值为5.1,紧组合的平均ratio值为19.1。

|
图 3 不同截止高度角ratio值 Fig. 3 Ratio values of different cut-off height angles |
表 1(单位%)为以ratio值为3和5作为成功固定模糊度的阈值时,不同截止高度角下松组合与紧组合的模糊度固定成功率。从表中可以看出,当以ratio=3作为模糊度成功固定的阈值时,随着卫星截止高度角的增大,紧组合相对松组合的模糊度固定成功率有了明显提高。其中,当卫星截止高度角为10°和20°时,紧组合相对松组合的模糊度固定成功率没有明显提高; 而当截止高度角为30°和40°时,模糊度固定成功率分别提高了14.72%和36.04%,提升较为明显。当选择ratio=5作为检验模糊度成功固定的阈值时,截止卫星高度角在10°、20°、30°和40°时,GPS系统平均卫星数量分别为9颗、7颗、5颗和4颗,BDS系统平均卫星数量分别为11颗、9颗、8颗和6颗,紧组合相对松组合的模糊度固定成功率分别提高10.04%、17.26%、31.74%和42.85%。因此,随着检验模糊度成功固定标准的严格,紧组合相对松组合提升模糊度固定成功率的效果更加明显。
|
|
表 1 不同截止高度角模糊度固定成功率 Tab. 1 Fixed rate of angle ambiguity of different cut-off heights |
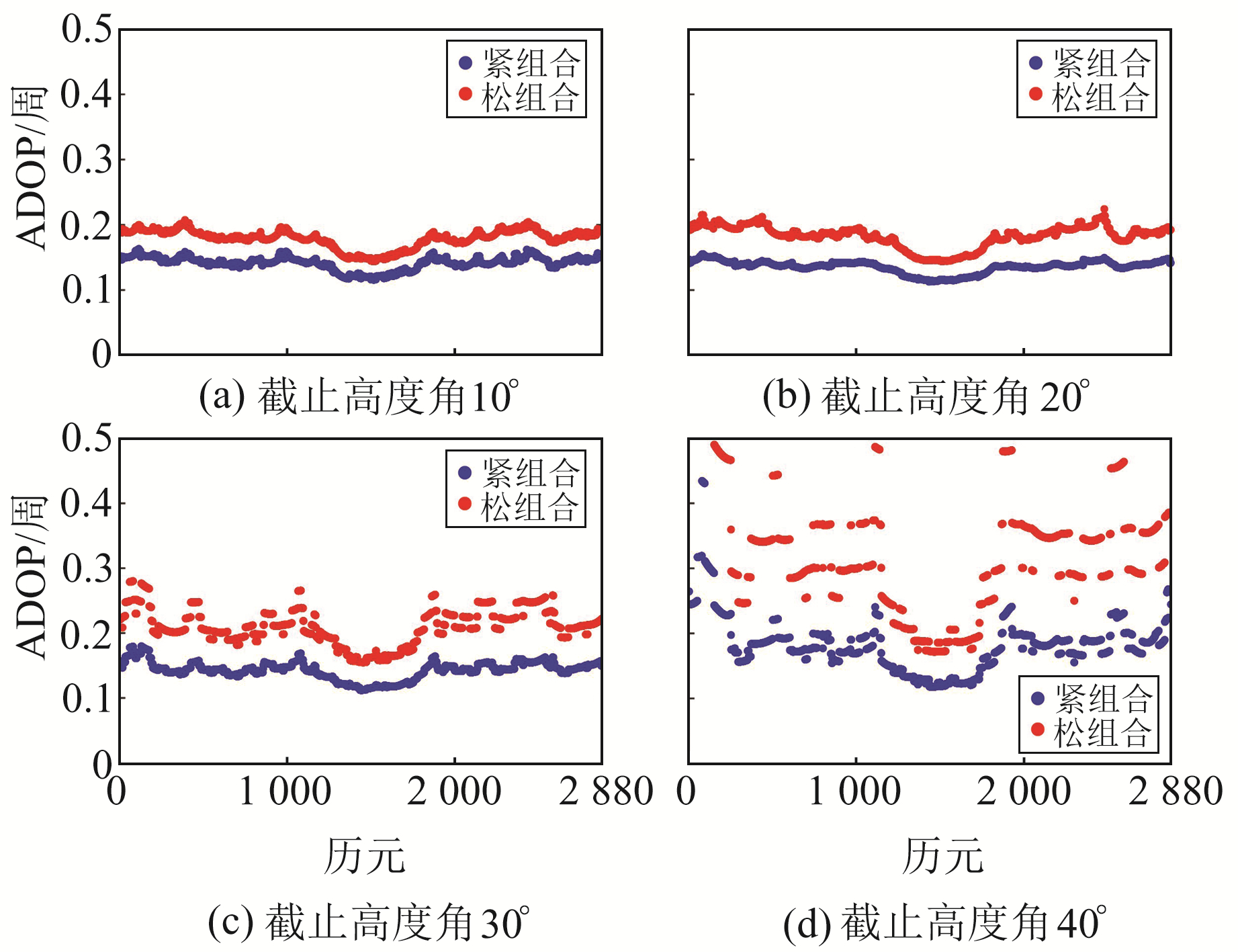
图 4为不同截止高度角下GPS/BDS单频松组合与紧组合的模糊度精度衰减因子(ADOP),由图可知,相比于松组合模型,使用紧组合模型后ADOP值有了显著降低,并且随着截止高度角的增大,ADOP值的降低效果越明显。不同截止高度角下ADOP的平均值统计见表 2。
|
图 4 不同截止高度角的ADOP Fig. 4 ADOP with different cut-off height angles |
|
|
表 2 不同截止高度角ADOP平均值 Tab. 2 ADOP mean values of different cut-off height angles |
表 3(单位%)为松组合与紧组合在E、N、U三方向定位误差小于1 cm的历元占全部历元的百分比,从表中可以看出,当截止高度角为10°和20°时,松组合与紧组合的定位精度差别不大,绝大多数历元的定位误差都在1 cm之内; 当截止高度角为30°时,紧组合1 cm以内的误差相对松组合在E、N方向所占比例提升约4%,U方向提升约14%;当截止高度角为40°时,紧组合的定位效果明显优于松组合,1 cm以内误差在E、N方向所占比例提升23%以上,U方向提升14%以上。
|
|
表 3 定位误差小于1 cm的历元所占全部历元百分比分布 Tab. 3 The percentage distribution of all calendars with positioning error less than 1 cm |
本文详细推导了短基线下GPS-L1/BDS-B1非重叠频率紧组合相对定位的模型与算法,论述了非重叠频率紧组合与重叠频率紧组合的处理区别,并对GPS-L1/BDS-B1非重叠频率的DISB稳定性进行分析。在DISB稳定的情况下可事先对其进行标定,将标定结果代入后续计算可以增加冗余观测量,有效提高模糊度解算的效率。利用短基线数据进行实验验证后发现,GPS-L1/BDS-B1间伪距与相位DISB均具有很好的时域稳定性,在使用单频单历元处理模式下,随着截止高度角的增加,使用事先标定DISB的紧组合相对定位模型比使用传统松组合模型的模糊度固定率提高3%~42%,平均ratio值提升25%~275%。在定位精度方面,当截止高度角为10°和20°时,卫星数量充足,紧组合与松组合的定位效果无太大区别; 当截止高度角为30°和40°时,卫星数量稀少,紧组合的定位效果优于松组合。
致谢: 感谢澳大利亚科廷大学(Curtin University)提供GNSS实验数据。
| [1] |
杨元喜, 陆明泉, 韩春好. GNSS互操作若干问题[J]. 测绘学报, 2016, 45(3): 253-259 (Yang Yuanxi, Lu Mingquan, Han Chunhao. Some Notes on Interoperability of GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 253-259)
(  0) 0) |
| [2] |
Julien O, Alves P, Cannon M E, et al. A Tightly Coupled GPS/GALILEO Combination for Improved Ambiguity Resolution[C]. Proceedings of the European Navigation Conference, Graz, 2003
(  0) 0) |
| [3] |
Julien O, Cannon M E, Alves P, et al. Triple Frequency Ambiguity Resolution Using GPS/GALILEO[J]. European Journal of Navigation, 2004, 2(2): 51-57
(  0) 0) |
| [4] |
Odijk D, Teunissen P J G. Characterization of between-Receiver GPS-Galileo Inter-System Biases and Their Effect on Mixed Ambiguity Resolution[J]. GPS Solutions, 2013, 17(4): 521-533 DOI:10.1007/s10291-012-0298-0
(  0) 0) |
| [5] |
Paziewski J, Wielgosz P. Accounting for Galileo-GPS Inter-System Biases in Precise Satellite Positioning[J]. Journal of Geodesy, 2015, 89(1): 81-93 DOI:10.1007/s00190-014-0763-3
(  0) 0) |
| [6] |
张小红, 吴明魁, 刘万科. Beidou B2/Galileo E5b短基线紧组合相对定位模型及性能评估[J]. 测绘学报, 2016, 45(增2): 1-11 (Zhang Xiaohong, Wu Mingkui, Liu Wanke. Model and Performance Analysis of Tightly Combined Beidou B2 and Galileo E5b Relative Positioning for Short Baseline[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 1-11)
(  0) 0) |
| [7] |
吴明魁, 刘万科, 张小红, 等. GPS/Galileo/BDS-3试验星短基线紧组合相对定位性能初步评估[J]. 武汉大学学报: 信息科学版, 2020, 45(1): 13-20 (Wu Mingkui, Liu Wanke, Zhang Xiaohong, et al. Initial Assessment of Tightly Combined Relative Positioning for Short Baselines with Observations from GPS, Galileo, and BDS-3 Experimental Satellites[J]. Geomatics and Information Science of Wuhan University, 2020, 45(1): 13-20)
(  0) 0) |
| [8] |
蒲亚坤, 袁运斌, 丁文武, 等. GPS/BDS-2/Galileo混合双差相对定位模型应用于短基线精密定位研究[J]. 大地测量与地球动力学, 2020, 40(1): 56-61 (Pu Yakun, Yuan Yunbin, Ding Wenwu, et al. GPS/BDS-2/Galileo Mixed Double Difference Relative Positioning Model Applied to Short Baseline Precise Positioning[J]. Journal of Geodesy and Geodynamics, 2020, 40(1): 56-61)
(  0) 0) |
| [9] |
Gao W, Meng X L, Gao C F, et al. Combined GPS and BDS for Single-Frequency Continuous RTK Positioning through Real-Time Estimation of Differential Inter-System Biases[J]. GPS Solutions, 2017, 22(1): 1-13
(  0) 0) |
| [10] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82 DOI:10.1007/BF00863419
(  0) 0) |
| [11] |
楼益栋, 龚晓鹏, 辜声峰, 等. GPS/BDS混合双差分RTK定位方法及结果分析[J]. 大地测量与地球动力学, 2016, 36(1): 1-5 (Lou Yidong, Gong Xiaopeng, Gu Shengfeng, et al. An Algorithm and Results Analysis for GPS+BDS Inter-System Mix Double-Difference RTK[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 1-5)
(  0) 0) |
| [12] |
Deng C L, Tang W M, Liu J N, et al. Reliable Single-Epoch Ambiguity Resolution for Short Baselines Using Combined GPS/Beidou System[J]. GPS Solutions, 2014, 18(3): 375-386 DOI:10.1007/s10291-013-0337-5
(  0) 0) |
| [13] |
Gendt G, Altamimi Z, Dach R, et al. GGSP: Realisation and Maintenance of the Galileo Terrestrial Reference Frame[J]. Advances in Space Research, 2011, 47(2): 174-185 DOI:10.1016/j.asr.2010.02.001
(  0) 0) |
| [14] |
Wang J L, Knight N L, Lu X C. Impact of the GNSS Time Offsets on Positioning Reliability[J]. Journal of Global Positioning Systems, 2011, 10(2): 165-172 DOI:10.5081/jgps.10.2.165
(  0) 0) |
| [15] |
吴仁攀. GPS/Galileo紧组合实时相对定位模型与方法研究[D]. 武汉: 武汉大学, 2018 (Wu Renpan. Research on Model and Method for GPS/Galileo Tight Combined Real-Time Relative Positioning[D]. Wuhan: Wuhan University, 2018)
(  0) 0) |
2. College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2021, Vol. 41
2021, Vol. 41

