精密单点定位技术(precise point positioning,PPP)利用IGS提供的精密星历和卫星钟差,基于载波相位观测值可实现dm~mm级高精度定位[1],而海潮负荷导致的固体地球形变可达cm级[2],在一定程度上制约了定位精度,因此在参数解算过程中需要考虑其引起的站点位移影响。在建模方面,现有全球海潮模型包括法国的FES,美国的GOT、TPXO,德国的HAMTIDE及日本的NAO等诸多种类[3],它们在世界各个区域特别是部分沿海及岛屿地区的适用性不尽相同[4-9]。
前人关于海潮负荷对世界范围PPP的影响程度及空间特征方面的研究多局限于中国及周边地区,未顾及收敛时间,且对FES2004与GOT4.7所属的系列高精度海潮模型在全球PPP中的比较及潮波差异特征分析较少。因此,本文采用二者改正前后全球20个IGS基准站的GPS观测数据进行24 h静态PPP和动态PPP解算,对比分析模型改正前后的解算结果,并就NIST、XMIS站的位移差异频谱和2种海潮模型下的潮波参数展开深入研究,对于全球范围PPP中择优选取适宜的海潮模型与局部地区模型的适用性等研究具有一定意义。
1 精密单点定位的函数模型本文采用无电离层组合模型[10]进行PPP解算,该模型消除了电离层1阶项的影响,大大减少了待估参数,且模型较为简单,在定位、授时应用中解算位置及接收机钟差参数时无需考虑电离层延迟量的影响[10]; 另外,由于IGS分析中心提供的精密钟差产品也是依托无电离层模型得到的,因此选择该模型进行PPP解算。其观测方程为[10]:
| $ \left\{ {\begin{array}{l} {{P_{{\rm{IF}}}} = \rho + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + T + }\\ {{b_{r, {\rm{IF}}}} - b_{{\rm{IF}}}^{\rm{s}} + \delta {\rho _{{\rm{mul}}, {P_{{\rm{IF}}}}}} + {\varepsilon _{{P_{{\rm{IF}}}}}}}\\ {{\mathit{\Phi } _{{\rm{IF}}}} = \rho + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + T - {\lambda _{{\rm{IF}}}}{N_{{\rm{IF}}}} + }\\ {{B_{{\rm{r}}, {\rm{IF}}}} - B_{{\rm{IF}}}^{\rm{s}} + \delta {\rho _{{\rm{mul}}, {\mathit{\Phi }_{{\rm{IF}}}}}} + {\varepsilon _{{\mathit{\Phi }_{{\rm{IF}}}}}}} \end{array}} \right. $ | (1) |
式中,PIF、ΦIF分别为经过地球潮汐、天线相位中心偏差等各项改正后的无电离层伪距和载波相位观测值,ρ为卫星至接收机的几何距离,c为光速,δtr、δts分别为接收机钟差和卫星钟差,T为对流层延迟,λIF为无电离层载波相位观测值的波长,NIF为无电离层组合模糊度,br, IF、bIFs分别为接收机端和卫星端伪距硬件延迟,Br, IF、BIFs分别为接收机端和卫星端相位未校准硬件延迟(uncalibrated phase delay,UPD),δρmul, PIF、δρmul, ΦIF为伪距和相位观测值的多路径误差,εPIF和εΦIF为测量噪声。
2 海潮负荷改正海潮负荷效应是指地球对海潮负载的响应,它会引起地面测站位置的周期性形变,影响量值随着观测位置的不同而异,且越靠近海岸地区对测站位置的影响越大[2, 6]。海潮负荷位移在计算过程中可表示为11个分潮波的叠加[11],即
| $ \Delta c = \sum\limits_{j = 1}^{11} {{f_j}} {A_{cj}}\cos \left( {{\omega _j}t + {\chi _j} + {u_j} - {\mathit{\Phi }_{cj}}} \right) $ | (2) |
式中,Δc表示测站t时刻在E、N、U三方向的海潮负荷位移分量; j(1≤j≤11)表示11个主要海潮分潮,包括4个半日分潮M2、S2、N2、K2,4个全日分潮K1、O1、P1、Q1,3个长周期潮Mf、Mm、Ssa,其余潮波可以通过插值获取; fj和uj分别为分潮波j的交点因子和订正角,与月球轨道升交点的经度有关; Acj和Φcj分别为分潮波j在测站相应方向的振幅和相位,可凭借给定的海潮模型求得; ωj和χj分别为分潮波j的角频率和天文幅角初相。本文在PPP中分别计算3个坐标分量的海潮负荷位移,在每次卡尔曼滤波过程中改正至观测方程式右侧的坐标参数上。
海潮负荷导致的地壳形变对测站U方向定位产生的误差较大,其中半日潮和周日潮误差在GNSS单天解中大部分都能被有效消除[2, 6],相比之下,其对短时PPP的影响则更加显著。海潮负荷的精度主要取决于海潮模型的精度[12],不过就现阶段来说,全球海潮模型很难达到以理想精度适用于大陆架、陆海交界等局部特殊区域,所以对不同模型之间的比较分析具有一定的必要性。本文分别采用FES2004和GOT4.7两种现代高精度海潮模型对海潮负荷位移进行改正,其中前者基于流体动力学方程,同化了671个验潮站、337个T/P卫星交叉点数据和1 254个ERS-2卫星交叉点数据[3],分辨率高达0.125°×0.125°; 后者则是经验模型,直接根据T/P、ERS-1/2、GFO及Jason-1卫星测高数据反演得到,但未加入验潮站资料,分辨率较FES2004稍低,为0.5°×0.5°。
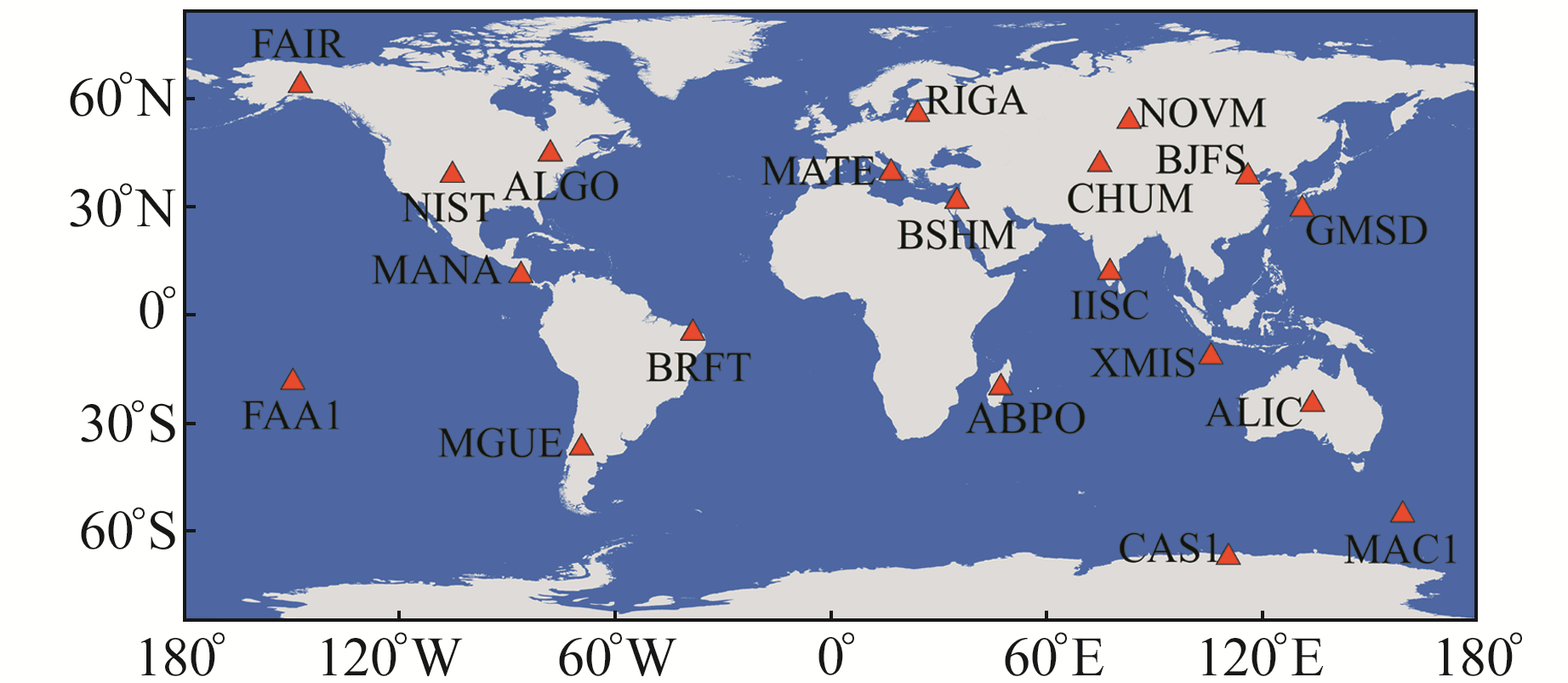
3 算例分析 3.1 站点选取与解算策略综合考虑南北半球、内陆与沿海地区、岛屿、远洋、低纬度与中高纬度地区等地理因素的影响,以便能够从全局反映世界范围内不同区域海潮负荷的形变程度和2种海潮模型的改正效果及区别,选择全球20个具代表性的IGS基准站的观测数据,利用RTKLIB软件进行PPP解算。沿海站点的选取不仅限于边缘海地带,同时充分顾及与陆地接触颇多的陆间海、内陆海沿岸,而岛屿站点所处地区则包括大陆岛、远海岛屿等多种类型。对内陆来说,尽管海潮负荷造成的地表形变程度较小,但仍需兼顾平原、高原、山地等一些具有不同地形特征的区域,以避免单一地理环境所带来的片面性和偶然性。表 1和图 1分别给出了具体解算策略及所选测站在全球的分布情况。
|
|
表 1 PPP解算策略 Tab. 1 PPP solution strategy |
|
图 1 20个IGS基准站的全球分布 Fig. 1 Global distribution of 20 IGS reference stations |
按照表 1策略进行静态PPP解算,并以IGS提供的测站坐标真值为基准,将获得的各站点三维坐标残差序列及均方根值(RMS)作为评定外符合精度的指标。计算2019-10-01 20个IGS基准站的坐标误差RMS和收敛时间,收敛历元参考文献[13]使用的方法来确定,当某一历元及其后续15 min内各历元测站空间位置误差皆低于5 cm的阈值时,认为解算结果收敛。结果发现,2种模型的改正效果在全球20个IGS基准站相差很小,均未超过亚mm级水平,改正后坐标收敛时间较先前平均缩短了6%,缩短量为4 min,说明顾及海潮负荷形变对静态PPP收敛速度会有微小提升。图 2将所选站点按字母顺序编号,列出了形变处理前后各站点坐标误差RMS之差与收敛时间的提升率,由于2种海潮模型在静态PPP中的差异非常小,这里仅给出FES2004模型的情况。结合图 2数据进行分析可知,海潮改正对U方向精度的提升最明显,E方向次之,N方向最小; 去除形变后U方向的精度提升量有30%超过1 mm,在位于巴西东北部沿海的BRFT站达到8 mm,在这些代表性区域内即使实施长期静态PPP也需重视负荷形变因素的干扰。对于以马来群岛附近的XMIS站、大隅诸岛GMSD站及前面所提的BRFT站为代表的岛屿及陆海交界地带,E或N方向的改正效果不够理想,反映2种全球海潮模型在世界范围内的准确性仍各有高低,特别是在这些站点所处典型区域周边表现不佳,该现象在一定程度上也归因于E、N两方向的海潮负荷形变量本身较小,对局部地区模型精度的变化更加敏感。在收敛时间方面,改正后中美海沟附近MANA站、马达加斯加岛ABPO站等沿海及岛屿站点提升明显,最高达30%,这与RMS差值的地理特征基本一致,但同样存在改正后收敛速度变慢的情况,并多集中于岛屿及陆海交界地带,其中南极大陆周边CAS1站最为突出,但该站U方向精度改善良好,具体原因需进一步分析,说明海潮改正对收敛时间的影响具有不确定性。

|
图 2 改正前后全球IGS站坐标误差RMS之差与收敛时间提升率 Fig. 2 Difference of the coordinate error RMS and upgrade rate of convergence time for global IGS station before and after correction |
根据20个IGS基准站的静态观测数据进行动态PPP解算,相较于静态PPP,动态PPP可以更加直接、实时地反映潮汐对测站位置产生的影响及其空间和时序特征。其中,接收机位置、钟差参数采用白噪声过程进行状态预测,在各历元状态更新前将参数值及方差重新初始化,初始值均根据伪距单点定位求得[14],方差为3 600 m2,对流层天顶延迟、水平梯度参数按照随机游走过程进行状态预测,前者及其方差初值均使用模型估计,过程噪声为10-4 m/
图 3为2019-10-01全部站点距面积超过10 000 km2的岛屿和陆地板块海岸线的最近距离(顾及各站至海岸线的距离相差较大,将上限设为2 000 km,并将起始刻度设到零值以下)及采用GOT4.7海潮模型改正前后点位差异的最大值与最小值,同时通过两者之间的差值可以直观体现1 d内站点位移的变化量。统计结果显示,海潮负荷在靠近海岸线或岛屿处测站1 d内引起的位移变化幅度与最大量普遍高于内陆地区,且位移峰值和谷值呈现出明显的对称性,实际表现为大小相近、方向相反的矢量。具体来说,U方向最大位移在BRFT站达到5 cm,在一些近海岛屿站点为3 cm左右,而该值在以FAA1站、MAC1站为代表的远海岛屿站点及若干内陆测站相对较小,不过也可达到cm级,可见对于PPP解算,尤其是实时或短时间PPP,沿海及岛屿区域的海潮负荷影响不容忽视。但仔细观察能发现,海潮负荷并非单纯随站点距海岸线越近越大,以波罗的海与地中海附近RIGA、BSHM、MATE等站为代表,三者依次距海岸线9 km、4 km、29 km,位移极值却停留至mm水平,只与陆地站点大致相当甚至略低。显著形变主要还是集中在大洋沿岸,陆间海、内陆海周边则不然,具体原因可能是两处海域的海洋环境、潮汐系统均比较封闭,前者位于亚欧板块内部,与其距离最近的北海、挪威海等相对开阔的海域被日德兰半岛、斯堪的纳维亚半岛及西兰岛、菲英岛在内的众多岛屿严重阻隔; 而后者则被亚欧和非洲两片大陆包围,几乎仅受来自狭窄的直布罗陀海峡的北大西洋潮汐作用,可见二者皆与远洋区域联系不够紧密,大洋潮汐运动对其影响较小。

|
图 3 各IGS站至海岸线距离与动态PPP中海潮负荷1 d内引起点位差异的极值 Fig. 3 The distance between each IGS station and the coastline and the extreme value of the point difference caused by the ocean tide load in the dynamic PPP within one day |
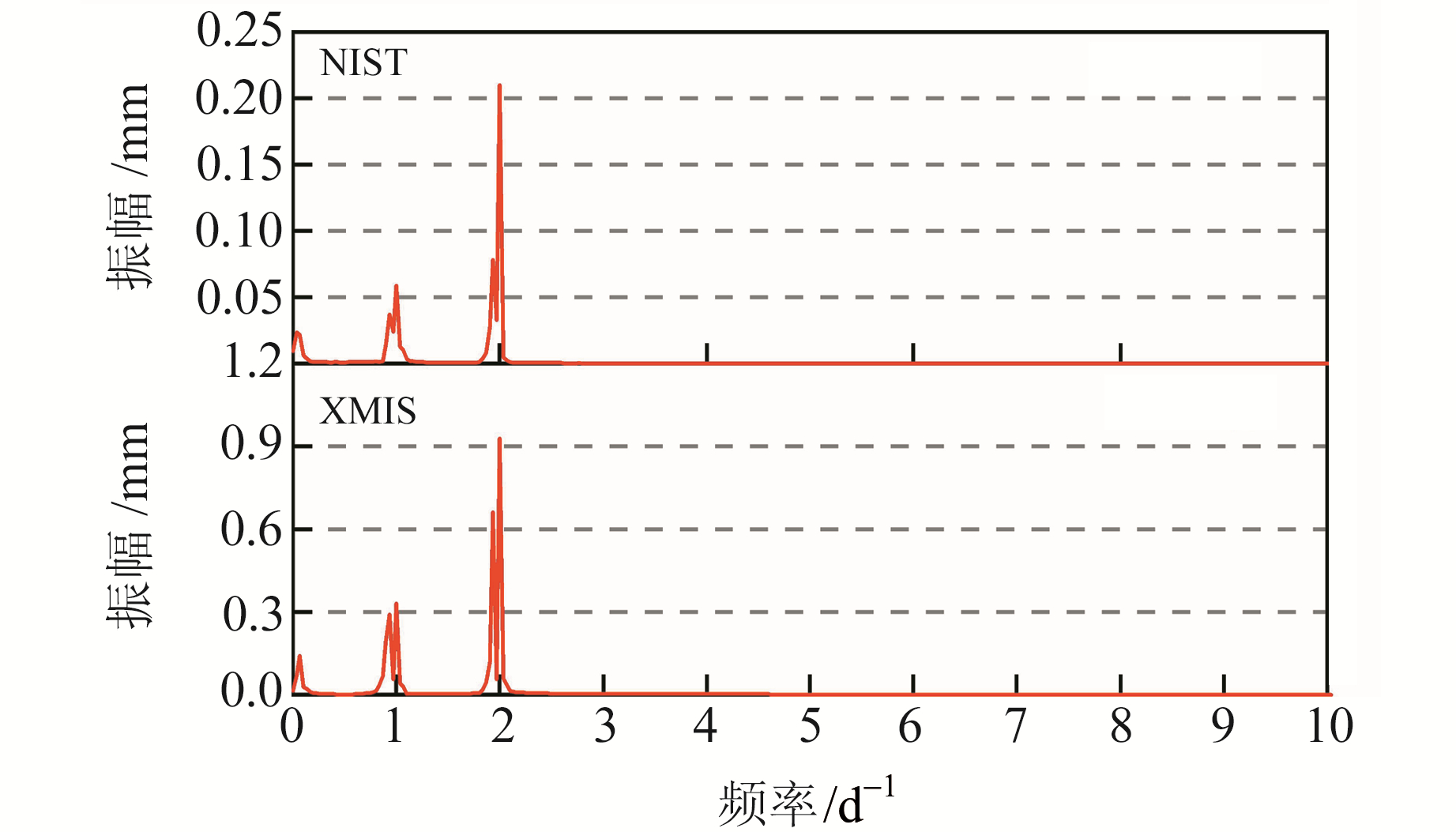
计算获得NIST站和XMIS站2019-09-22~10-21连续1个月期间由海潮负荷引起的E、N、U三方向位移量,求出2种模型的位移差值,并通过快速傅里叶变换(FFT)获得差值序列的振幅频谱。限于篇幅,这里仅给出测站U方向的情况,结果如图 4所示。从振幅值来看,2种海潮模型的差值在XMIS站比NIST站更加显著,这是由地理位置导致的,前者地处圣诞岛,位于印度洋板块和亚欧板块交界地带,并靠近马来群岛; 而NIST站则隶属美国大平原以西地区,模型适用性及差别程度存在不同。同时,基于FES2004与GOT4.7模型计算的NIST站和XMIS站U方向的海潮负荷位移差值也反映出这一特点,两者在连续1个月内最大分别为0.4 mm和2.3 mm,能够达到mm级,NIST站位移差值RMS只占XMIS站的19.3%。以XMIS站为例,由图 4可见,位移差值主要集中于0.066 7/d、0.933 3/d、2/d这3个频率,呈现出与海潮本身类似的半日、周日和半月周期,并且半日潮形变差值最高,周日潮次之,半月潮最低,这与三者导致的地壳形变量呈正相关趋势。
|
图 4 两种模型下U方向位移差值的振幅频谱 Fig. 4 Amplitude spectrum of displacement difference in the up direction under two models |
由前文可知,海潮负荷位移的差值随时间呈周期性变化,为探讨FES2004与GOT4.7模型的全球地理分布特征,从各潮波参数角度对二者作综合比较。单个参考点k方向2种海潮模型间差值Δjk与所有参考点的均方根差值RMS(Δjk)按如下公式进行衡量[5, 15]:
| $ \begin{array}{l} {\mathit{\Delta }_{jk}} = \mid {A_{{\rm{FES}}}}\left[ {\cos \left( {{\mathit{\Phi }_{{\rm{FES}}}}} \right) + {\mathop{\rm isin}\nolimits} \left( {{\mathit{\Phi }_{{\rm{FES}}}}} \right)} \right] - \\ \;\;\;\;\;{\left. {{A_{{\rm{GOT}}}}\left[ {\cos \left( {{\mathit{\Phi }_{{\rm{GOT}}}}} \right) + {\mathop{\rm isin}\nolimits} \left( {{\mathit{\Phi }_{{\rm{GOT}}}}} \right)} \right]} \right|_{jk}} \end{array} $ | (3) |
| $ \operatorname{RMS}\left(\Delta_{j k}\right)=\sqrt{\frac{1}{N} \sum\limits_{n=1}^{N} \Delta_{j k}^{2}} $ | (4) |
式中,A、Φ为分潮波j的振幅和相位,i为虚数单位,N为站点数目。这种方式比单独比较振幅或相位更能系统、全面地反映模型的总体区别,且充分考虑了二者对形变的共同贡献。图 5为GOT4.7模型下11个主要潮波在所有IGS站点U方向的振幅,及根据式(3)计算的2种模型下各潮波的差异。结果显示,M2分潮振幅一般要高于其他分潮,其值在沿海BRFT站、GMSD站、MANA站普遍超出或接近2 cm,最大达3.6 cm,在某些内陆站点则略小,通常只有mm级水平,这也充分反映了海潮负荷对近海岸区域的影响显著高于内陆地区; 同样,对于地中海和波罗的海沿岸的3个站点来说,其振幅值皆停留在6 mm以下,同内陆区域不相上下,与最大位移量的地理分布特征一致。相对而言,其他潮波振幅值仅有3%超过1 cm,比较突出的S2、K1、O1分潮平均振幅依次占M2分潮的37%、51%、40%,说明M2分潮对测站位移的影响程度比其他潮波高。另外,从图 5(b)中可以发现,2种模型间的差异主要集中在M2、S2与K1分潮,三者的均方根差异约为其他潮波的2~8倍,而3个长周期潮Mf、Mm、Ssa差别最小,说明各潮波差异水平与其自身对总体形变的贡献程度有一定关系。虽然图 5(b)也呈现出沿海地区较内陆地区更明显的特征,但不同的是,振幅、形变与内陆几乎无异的波罗的海沿岸RIGA站K1潮波差异量却相对较大,与边缘海一带及岛屿站点接近。U方向各潮波相差皆为亚mm级,表明2种全球海潮模型在20个IGS站具有较高的符合度。

|
图 5 GOT4.7模型下各分潮U方向振幅及2种模型下的潮波差异 Fig. 5 Amplitude in the up direction of each constituent under the GOT4.7 model and the difference of tide waves between the two models |
考虑到M2分潮在11个潮汐信号中对测站定位的影响程度较高,同时人类活动又很少涉及两极地区,故选择全球70°S~70°N范围,并基于FES2004和GOT4.7模型求取其U方向振幅与相位,所用程序包为SPOTL[16],通过式(3)衡量二者的总体差异,具体分布情况如图 6所示。从振幅及相位整体来看,2种模型的M2分潮差异在大陆板块内部最小,大西洋、印度洋等远洋次之,但基本也都能维持在亚mm级,太平洋区域则可能受众多群岛影响,差异分布稍显不均,南极大陆周边也仅浮动于1 mm上下。海湾、群岛、海峡和边缘海地带差异比较明显,尤其是加拿大北部海域,潮波参数普遍相差很大,达到2~12 mm,该地区90°~70°W、65°~70°N范围内的均方根差异超过了6 mm,印度半岛西部、阿纳姆地西北沿海港湾和珊瑚海西南海岸等地单点差异可超过8 mm,而在鄂霍次克海西部的尚塔尔群岛附近和安达曼海以北,差异极大值更是分别达到10 mm和13 mm,前者周边135°~142°E、53°~60°N区域内均方根差异达4 mm。此外,诸如科尔科瓦多湾、亚历山大群岛等地区附近均达到数mm,这种空间分布特征与§3.3中2种海潮模型在NIST站和XMIS站具有不同程度差别的情况相符。值得一提的是,2种模型在我国东部沿海地区的差值也可超过5 mm,因此在这些区域进行短期PPP时有必要根据实际情况选择适宜的全球海潮模型或联合局部地区近海海潮模型加以改正。潮波振幅很大程度上决定了负荷位移量的峰值,虽然模型差异与海潮负荷皆在沿海区域十分突出,但依照本文格网数据计算得出前者与振幅相关系数只有0.04,以形变很小的波罗的海地区为例,该处差异量却能达到1.6 mm,这与RIGA站的情况吻合。综上所述,两者于地理分布上无必然联系,所有站点的M2分潮均方根差值为0.5 mm,仅占平均振幅值的3.8%,可见2种海潮模型的差值相对于形变本身仍然很小。

|
图 6 基于2种模型计算的M2分潮U方向差异 Fig. 6 Difference in the up direction of M2 constituent calculated based on the two models |
本文针对20个IGS站点分析了海潮负荷对全球范围PPP的影响特征及FES2004、GOT4.7两种全球海潮模型改正对测站定位影响的差异,结果表明:
1) 在空间分布上,海潮负荷对大洋沿岸、岛屿地区PPP的影响要高于内陆地区,但在地中海、波罗的海等陆间海和内陆海域影响较小,形变程度与部分内陆地区相当甚至略低,并非单纯离海岸线越近越明显,由其引起的沿海测站U方向位移可以达到5 cm,1 d内的位移变化幅度也更大。
2) 海潮负荷在全球24 h静态PPP中对边缘海沿岸及岛屿地区测站坐标误差RMS的影响可达数mm,需要加以重视,但对该类区域某些站点E、N方向的改正效果较差,海潮负荷改正对静态PPP收敛速度的提升能达到30%。另外,2种模型的差值对世界范围PPP单天解的影响非常小。
3) FES2004和GOT4.7全球海潮模型下的M2、S2、K1分潮差异比其他分潮更大,从M2分潮U方向振幅及相位参数整体来看,2种模型在海湾、群岛和边缘海(特别是加拿大北部海域及鄂霍次克海附近)差异较大,最高可达13 mm,这种差异在地理分布上与海潮本身的大小无必然联系。基于2种模型计算的站点位移差异具有与海潮类似的周期性特征,在马来群岛附近可达数mm,且半日潮的形变差异要高于周日及半月潮。
| [1] |
张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250-256 (Zhang Xiaohong, Zuo Xiang, Li Pan, et al. Convergence Time and Positioning Accuracy Comparison between BDS and GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 250-256)
(  0) 0) |
| [2] |
张杰. GPS精密测量中的海潮负荷问题研究[D]. 武汉: 武汉大学, 2014 (Zhang Jie. Research on Ocean Tide Loading Problem in GPS Precision Surveying[D]. Wuhan: Wuhan University, 2014)
(  0) 0) |
| [3] |
张胜凯, 雷锦韬, 李斐. 全球海潮模型研究进展[J]. 地球科学进展, 2015, 30(5): 579-588 (Zhang Shengkai, Lei Jintao, Li Fei. Advances in Global Ocean Tide Models[J]. Advances in Earth Science, 2015, 30(5): 579-588)
(  0) 0) |
| [4] |
李大炜, 李建成, 金涛勇, 等. 利用验潮站资料评估全球海潮模型的精度[J]. 大地测量与地球动力学, 2012, 32(4): 106-110 (Li Dawei, Li Jiancheng, Jin Taoyong, et al. Accuracy Estimation of Recent Global Ocean Tide Models Using Tide Gauge Data[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 106-110)
(  0) 0) |
| [5] |
范文蓝, 姜卫平, 袁林果, 等. 不同海潮模型对中国沿海区域海潮负荷位移改正影响分析[J]. 大地测量与地球动力学, 2018, 38(6): 598-602 (Fan Wenlan, Jiang Weiping, Yuan Linguo, et al. Effects of Different Ocean Tide Models on OTL Correction in China's Coastal Areas[J]. Journal of Geodesy and Geodynamics, 2018, 38(6): 598-602)
(  0) 0) |
| [6] |
张杰, 李斐, 楼益栋, 等. 海潮负荷对GPS精密定位的影响[J]. 武汉大学学报: 信息科学版, 2013, 38(12): 1 400-1 404 (Zhang Jie, Li Fei, Lou Yidong, et al. Ocean Tide Loading Effect on GPS Precise Positioning[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1 400-1 404)
(  0) 0) |
| [7] |
Penna N T, King M A, Stewart M P. GPS Height Time Series: Short-Period Origins of Spurious Long-Period Signals[J]. Journal of Geophysical Research Atmospheres, 2007, 112(B2): B02 402
(  0) 0) |
| [8] |
赵红, 张勤, 黄观文, 等. 基于不同海潮模型研究海潮负荷对GPS精密定位的影响[J]. 大地测量与地球动力学, 2012, 32(5): 108-112 (Zhao Hong, Zhang Qin, Huang Guanwen, et al. Effect of Ocean Tide Loading on GPS Precise Positioning Based on Different Ocean Tide Models[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 108-112)
(  0) 0) |
| [9] |
吴志露, 刘焱雄, 何秀凤, 等. 基于近岸海岛GPS数据反演海洋分潮负荷影响[J]. 地球物理学报, 2017, 60(1): 61-69 (Wu Zhilu, Liu Yanxiong, He Xiufeng, et al. Inversion of Ocean Tidal Loadings of Marine Constituents Based on the GPS Measurements in the Offshore Islands[J]. Chinese Journal of Geophysics, 2017, 60(1): 61-69)
(  0) 0) |
| [10] |
张小红, 左翔, 李盼. 非组合与组合PPP模型比较及定位性能分析[J]. 武汉大学学报: 信息科学版, 2013, 38(5): 561-565 (Zhang Xiaohong, Zuo Xiang, Li Pan. Mathematic Model and Performance Comparison between Ionosphere-Free Combined and Uncombined Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 561-565)
(  0) 0) |
| [11] |
McCarthy D D, Petit G. IERS Technical Note No. 32: IERS Conventions(2003)[R]. Frankfurt am Main: IERS Conventions Centre, 2004
(  0) 0) |
| [12] |
刘经南, 张化疑, 刘焱雄, 等. GNSS研究海潮负荷效应进展[J]. 武汉大学学报: 信息科学版, 2016, 41(1): 9-14 (Liu Jingnan, Zhang Huayi, Liu Yanxiong, et al. Progress of Ocean Tide Loading Inversion Based on GNSS[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 9-14)
(  0) 0) |
| [13] |
刘帅, 孙付平, 郝万亮, 等. 整数相位钟法精密单点定位模糊度固定模型及效果分析[J]. 测绘学报, 2014, 43(12): 1 230-1 237 (Liu Shuai, Sun Fuping, Hao Wanliang, et al. Modeling and Effects Analysis of PPP Ambiguity Fixing Based on Integer Phase Clock Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1 230-1 237)
(  0) 0) |
| [14] |
T Takasu. RTKLIB ver. 2.4.2 Manual[EB/OL]. http://www.rtklib.com/prog/manual_2.4.2.pdf, 2013
(  0) 0) |
| [15] |
张小红, 马兰, 李盼. 利用动态PPP技术确定海潮负荷位移[J]. 测绘学报, 2016, 45(6): 631-638 (Zhang Xiaohong, Ma Lan, Li Pan. Determination of Ocean Tide Loading Displacements Using Kinematic PPP[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 631-638)
(  0) 0) |
| [16] |
Agnew D C. SPOTL: Some Programs for Ocean-Tide Loading[R]. San Diego: Scripps Institution of Oceanography, 2012
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

