2. 自然资源部大地测量数据处理中心,西安市友谊东路334号,710054
连续运行基准站是现代测绘基准体系建设的基础设施,需要利用实时卫星导航数据分析区域基准站空间的相对变化运动特征与影响量级,从而更好地指导区域参考框架的维护与使用。当前,国内外学者主要从2个方面进行区域参考框架的研究,一是从区域参考框架的实现方法与策略等方面进行研究[1-3],另一方面是从单基准站的时间序列分析站点的运动规律[1, 4-5]。总体来说,关于参考框架维护的研究大多以站点的时间序列与噪声特点为切入点,主要研究其长期变化规律,但高精度的参考框架需要区域框架内部相对稳定且随机影响量级较小。现有的区域参考框架的构建基本没有顾及非线性等影响因素,且非线性影响在不同方向的量级与规律不尽相同,因此从区域参考框架基线时间序列的时空运动规律出发,探讨区域框架的时空运动特性与随机影响对区域参考框架监测与维护的影响,对于区域参考框架的动态更新具有重要的指导意义。
通常基线的时间序列已削弱了部分公共误差的影响,但时序信号中同时含有区域框架内部构造形变与非构造形变的残余影响,这些信息为精细化分析参考框架内在的运动规律与地质构造板块运动的相互作用提供了基础。本文以东北区域2005~2018年的基线时间序列为基础,分析东北区域参考框架的相对变化规律与特征,剖析引起其空间变化的内在机理,定性与定量分析非线性影响与空间运动规律对东北区域参考框架的影响,以用于东北区域参考框架的维护与监测。
1 区域数据处理思路本文对2005-01-01~2018-12-31中国东北地区和环渤海区域的24个陆态网基准站点数据进行处理,数据的采样间隔为30 s,不采用分区解算,处理步骤如下:
1) 首先利用GAMIT 10.61软件对陆态网基准站点的观测数据(CHUN、HLAR、HRBN、SUIY站从2005年开始,其余站点从2011年或之后有数据开始)进行处理,获得基准站点和国内及周边IGS站的单日松弛解; 再利用glred模块综合单日松弛解,并以12个国内和周边IGS站在ITRF2014下的坐标和速度为基准,使用eq_rename文件对由地震产生的阶跃数据进行改正; 最后从约束平差结果文件中获取东北陆态网站点的坐标和基线时间序列。
2) 采用Delaunay三角剖分算法构建基线序列,并进行预处理和频谱分析,得出大尺度下框架内部的相对运动特征与非线性影响。基线时序的预处理包括阶跃项探测、粗差剔除、数据插值等[6],针对基线序列的粗差,本文以时间序列的3倍中误差为准则对粗差点进行剔除[7]。另外,对GNSS基线时序进行分析时要求时序均匀采样,而由于受解算误差和粗差剔除等的影响,GNSS基线时序是不连续的时序,因此需要对基线数据进行插值以形成等间隔时序。
3) 对步骤2)中预处理后的基线序列进行时空变化特征分析,采用主成分分析方法提取共模误差影响,分析基准站点间的随机影响,为精细化构建区域参考框架提供技术参考。
2 时间序列分析方法 2.1 常规模型GNSS站点的时间序列包含速度项、阶跃项、周年项和半周年项等非构造信号,GNSS站点的坐标时间序列拟合函数模型为[8]:
| $ \begin{aligned} y\left(t_{i}\right)=& a+b t_{i}+c \sin \left(2 \pi t_{i}\right)+d \cos \left(2 \pi t_{i}\right)+\\ & e \sin \left(4 \pi t_{i}\right)+f \cos \left(4 \pi t_{i}\right)+\\ & \sum\limits_{j=1}^{n_{g}} g_{j} H\left(t_{i}-T_{h j}\right)+v_{i} \end{aligned} $ | (1) |
式中,y(ti)为基线时间序列,a为初始位置,b为速率,c、d、e、f分别为年周期、半年周期项系数;
基于式(1)的函数模型,可将基线时间序列写成式(2)的矩阵形式。利用MATLAB软件输入原始基线时序L,通过式(2)求出X,并反算得到基线残差时间序列Δ。
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{BX}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} $ | (2) |
其中,BT=[B1T, B2T, …, BnT]; X =[a, b, c, d, e, f]T; L =[y(t1), y(t2), …, y(tn)]T; Bi=[1, ti, sin(2πti), cos(2πti), sin(4πti), cos(4πti)]。
2.2 周期项分析基线中隐含了站点间的非线性影响规律,本文采用傅里叶变换与Lomb-Scargle算法进行分析。傅里叶变换只能应用于均匀采样的时间序列,而Lomb-Scargle算法能克服CORS站不均匀采样的影响,消除由于时间间隔不等导致的虚假信号,使周期项估计准确[8]。
2.2.1 Lomb-Scargle算法Lomb-Scargle算法的归一化功率谱pY(ω)计算式为:
| $ p_{Y}(\omega)=\frac{1}{2 \sigma^{2}}\left\{\frac{\left(\sum\limits_{i=1}^{N} \Delta Y\left(t_{i}\right) \cos \left[\omega\left(t_{i}-\tau\right)\right]\right)^{2}}{\sum \cos ^{2}\left[\omega\left(t_{i}-\tau\right)\right]}+\right. \\ \;\;\;\;\;\;\;\;\;\frac{\left(\sum\limits_{i=1}^{N} \Delta Y\left(t_{i}\right) \sin \left[\omega\left(t_{i}-\tau\right)\right]\right)^{2}}{\sum \sin ^{2}\left[\omega\left(t_{i}-\tau\right)\right]} $ | (3) |
式中,ΔY(ti)=Y(ti)-Y、Y(ti)、Y和σ2分别为零均值时序、原时序、原时序均值和方差; ti为时刻,ω为角频率,τ为补偿常数,则有:
| $ \tan (2 \omega \tau)=\frac{\sum\limits_{i=1}^{N} \sin \left(2 \omega t_{i}\right)}{\sum\limits_{i=1}^{N} \cos \left(2 \omega t_{i}\right)} $ | (4) |
主成分分析是一种将多个指标转化为少数综合指标的特征提取方法,能提供原有指标的绝大部分信息,从而简化问题并直观反映问题的本质[9]。对于去趋势、去均值后的矩阵X,设其协方差矩阵B为n×n的对称满秩矩阵,则:
| $ b_{i j}=\frac{1}{m-1} \sum\limits_{k=1}^{m} x_{k i} x_{k j} $ | (5) |
对其进行特征值分解:
| $ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{V \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{V}}^{\rm{T}}} $ | (6) |
其中,VT为由矩阵 B对应的n个特征向量组成的正交矩阵,Λ为由矩阵 B的k个非零特征值组成的对角矩阵。协方差矩阵 B为满秩矩阵,对于 X的任何一行向量,第k个主成分可表示为:
| $ a_{k}=\sum\limits_{i=1}^{n} v_{j k} x_{j}, k=1, 2, \cdots, n $ | (7) |
将特征值降序排列,前几个特征值代表对残差值时序方差的最大贡献值,共模误差(CME)[10]可表示为:
| $ \varepsilon_{j}=\sum\limits_{i=1}^{p} v_{j i} a_{i} $ | (8) |
其中,p为主成分个数,在选取时一般要求所选特征值之和不低于全部特征值之和的80%[11]。
3 东北区域参考框架的时空特性分析东北区域基准站由于受外部环境、地质因素及其他非构造信号的影响而产生时空相对运动,分析基准站间的基线运动趋势并量化相邻区域基准站的随机影响对区域参考框架的建立具有重要意义。
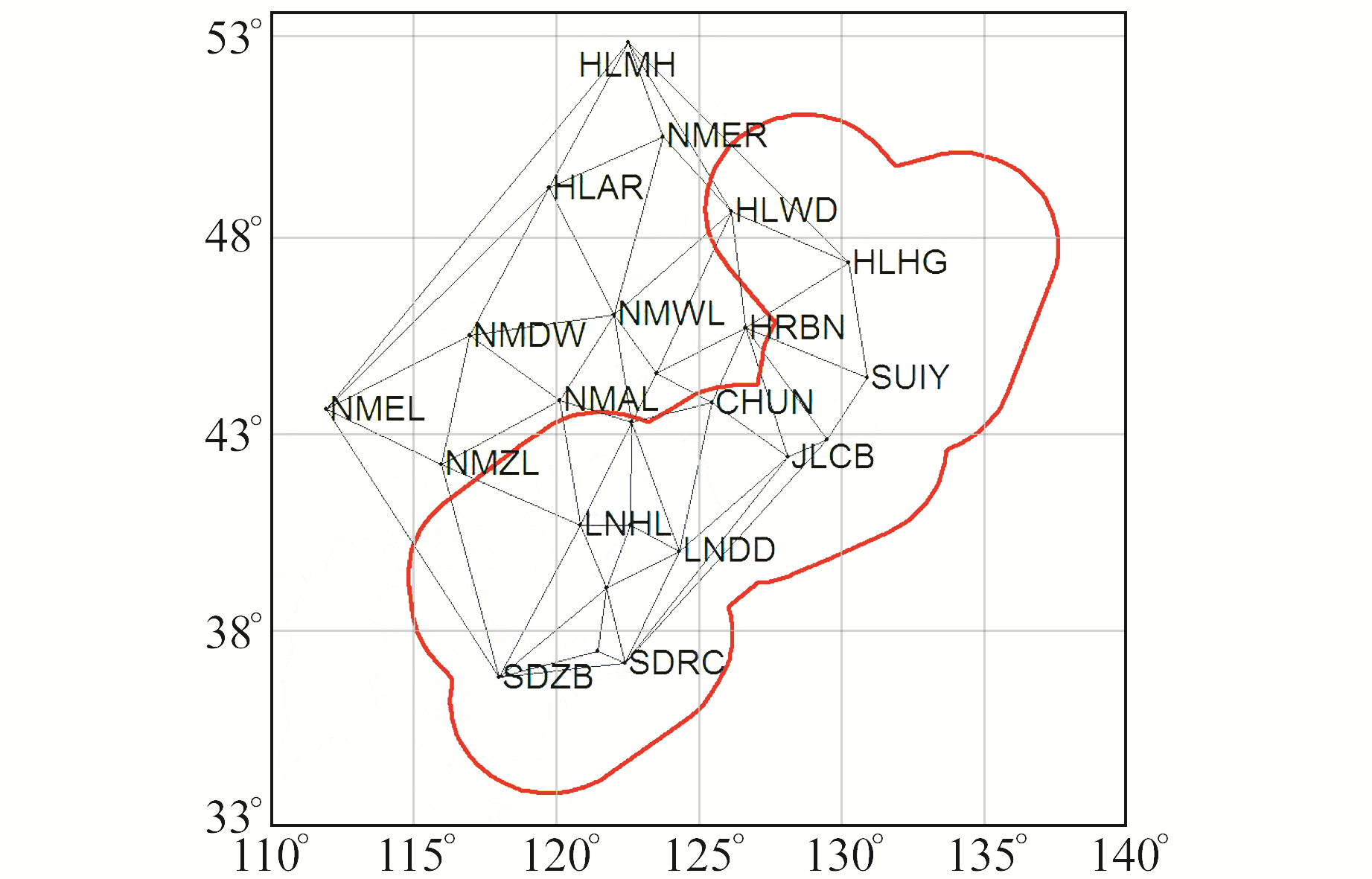
3.1 频谱分析将基线按地域分为内陆地区和近海地区2个部分,具体如图 1所示,图中沿海地区向内陆延伸350 km的地区用红色线条圈定,将圈定部分定义为近海地区,以分析不同属性区域对基线周期性产生的影响。利用Lomb-Scargle时频变换方法分别为2个地区进行非线性影响分析,所得周期项分析结果见表 1。因篇幅所限,本文仅列出部分基准站的时间序列及频谱分析结果。
|
图 1 东北区域基准站三角网及近海区域分布 Fig. 1 Triangulation network and offshore area distribution of northeast regional reference stations |
|
|
表 1 周期项分析 Tab. 1 Periodic term analysis |
由表 1可知,内陆地区的基线非线性影响在南北(N)、东西(E)、垂直(U)和基线长度(L)分量的时间序列中表现的周期数以年周期和半年周期为主,主要周期数的百分比依次为45%、52%、48%、45%;周期数仅为年周期的占比分别为34%、34%、28%、38%;2个长周期和1个半年周期的占比最小,分别为21%、14%、24%、17%;近海地区的周期项影响与内陆地区的统计结果类似。总体来看,基线序列中非线性影响主要表现为以年周期和半年周期为主,个别存在超过1 a的长周期影响,因此本文以年周期和半年周期进行时间序列模型的推算。
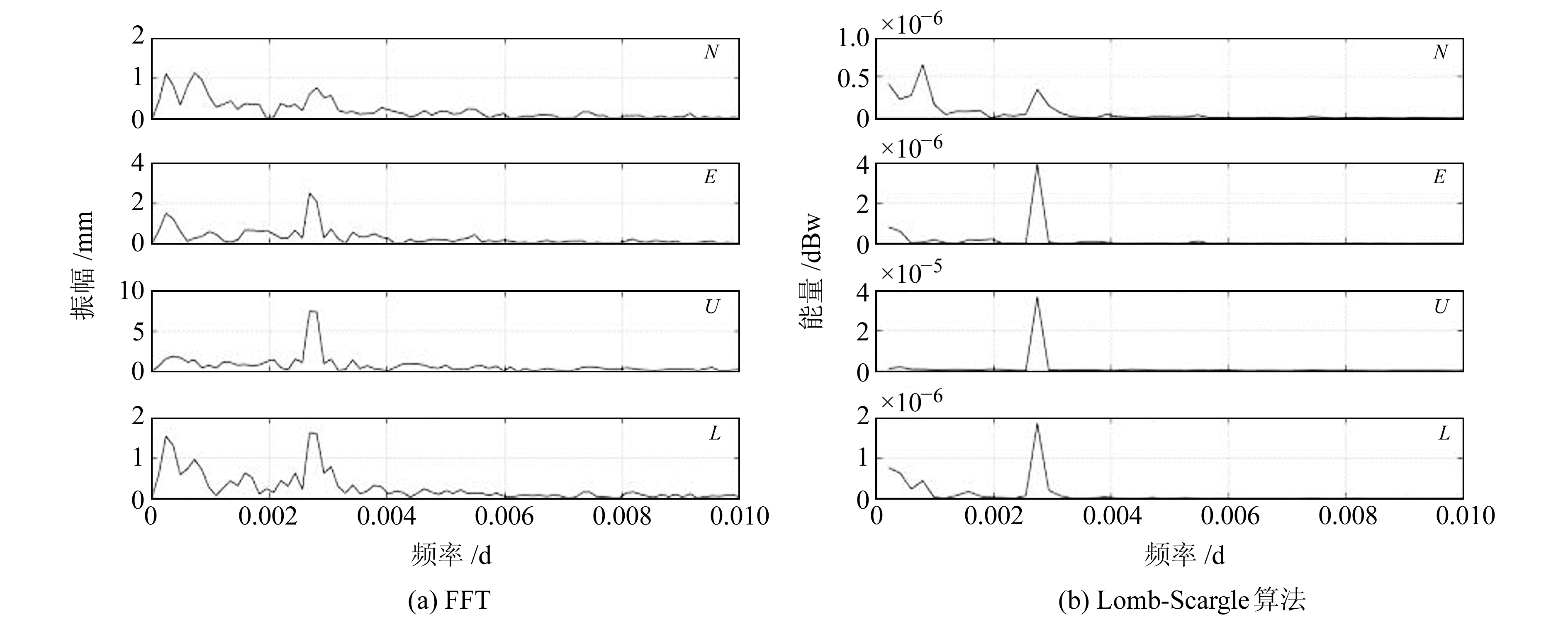
由图 2中CHUN-HRBN基线时频变换结果可以看出,Lomb-Scargle算法较快速傅里叶变换(FFT)更能准确地得到与真实情况相符的结果。基线中N、E、U、L四个分量的时间序列呈明显的周期性,基线时序出现明显的年周期,其余基线序列也表现出相似的特征,有些基线同时出现周期约2 a的长周期特性。
|
图 2 FFT和Lomb-Scargle算法CHUN-HRBN基线时频变换结果 Fig. 2 Time-frequency transform results of CHUN-HRBN baseline using FFT and Lomb-Scargle |
本文仅以CHUN-HRBN基线为例,其他基线序列表现出相似特征。由图 3可以看出,未剔除共模误差的残差序列中有较明显的周期性,说明时序中含有由非构造信号引起的共模误差,且共模误差在各方向均呈现出一定的随机性; 从共模误差剔除后的残差序列来看,基线的水平分量与垂直分量趋于平稳,基线长度序列也比较稳定。

|
图 3 CHUN-HRBN基线残差序列剔除CME前后对比 Fig. 3 Comparison of residual CHUN-HRBN baseline series before and after CME elimination |
通过相邻区域基线的共模误差分析,对每条基线各方向提取出的共模误差求绝对值的平均值,统计结果见表 2(单位mm)。
|
|
表 2 共模误差对各基线影响绝对值的平均值统计 Tab. 2 Statistics of the absolute mean value of the influence of CME on each baseline |
由表 2可知,共模误差对水平分量的影响约为1 mm,对垂直分量的影响最大,平均影响约为3 mm。采用构建三角网的方法虽能削弱部分公共误差的影响,但基线序列中仍存在共模误差的影响,因此在构建区域速度场模型及mm级参考框架时,共模误差是不容忽视的。
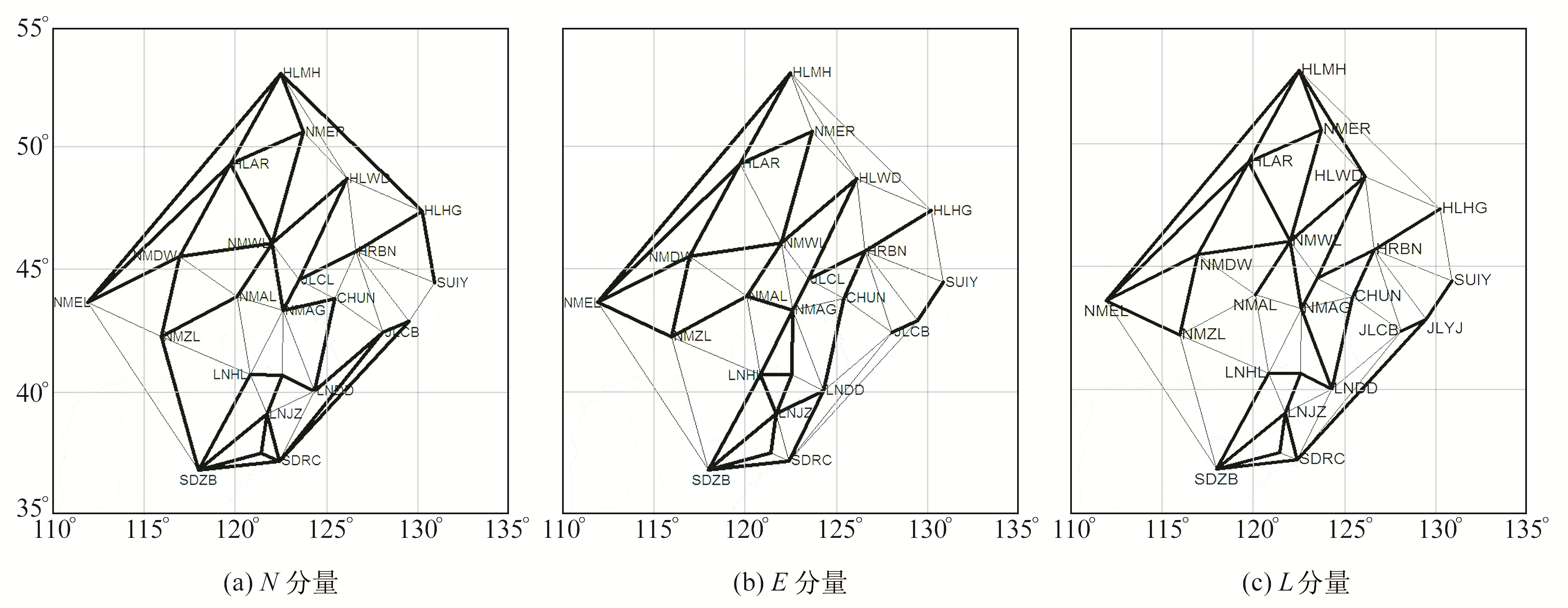
3.3 基线时空运动特征分析在空间尺度上对东北区域的基线进行分析,图 4为基线各分量年变化率的正负值,其中加粗线条表示基线年变化率为负值。
|
图 4 东北区域基线的年变化率分布 Fig. 4 Annual change rate distribution of the northeast regional baseline |
由图 4可以看出:
1) 长度逐年缩短的基线为年变化率为负值的基线,从N分量的年变化率来看,北东方向的基线有缩短趋势,且年变化率为负值的基线占比很大,均值为-1.2 mm/a; 有少部分北西方向的基线在N分量的年变化率为正值,说明这些基线在NS方向处于拉伸状态,均值为0.8 mm/a。
2) E分量的年变化率中北东方向的基线也有缩短趋势,这些缩短的基线均值为-1.3 mm/a,且从图中可以看出,E分量缩短的基线数量较多; 年变化率为正值的基线均值为1.2 mm/a,这些基线主要表现出在EW方向拉伸的趋势。
3) L分量的年变化率为负值的基线主要集中在北东与北西方向,近海和内陆地区都有明显表现,年变化率为负值的占比约56%,均值为-0.5 mm/a,表明这些基线长度在以每年0.5 mm的尺度缩短; 正值均值为0.9 mm/a,表明基线长度在以每年0.9 mm的尺度拉长。
4) 基线各分量在各方向的变化趋势可能来源于太平洋板块对欧亚板块的俯冲和日本海的弧形外张作用[2],也可能与基线两端所在块体的水平向差异运动有关。
3.4 基准站间随机影响分析基准站间的随机影响指的是各基准站在垂直和水平方向的运动趋势对基线在水平和垂直方向的运动趋势产生的影响。相邻区域基准站的随机影响主要通过求取剔除基线CME后各分量的残差序列的标准差来确定,统计基线各分量两站点间的随机影响结果见表 3(单位mm)。
|
|
表 3 基线各分量随机影响 Tab. 3 Random influence magnitude in each direction of baseline |
由表 3可知,4个分量中基线的随机影响均值分别为0.53 mm、0.72 mm、0.04 mm及0.27 mm,总体来看,基准站间的随机影响主要集中在NS与EW方向,对基线的长度影响较小。
4 结语通过对东北区域连续运行基准站网近14 a的基线数据进行空间运动规律、非线性影响及随机影响分析,得出以下结论:
1) 东北区域的基线周期性影响主要以年周期和半年周期为主,部分站点存在长周期影响。
2) 基线时间序列中的共模误差影响在水平与垂直方向的影响量级均在mm级,在垂直方向的平均影响最大,因此在mm级区域框架的维护中需要削弱该影响因素。
3) 从区域框架内部运动的随机影响统计来看,4个分量中基线的随机影响平均值分别为0.53 mm、0.72 mm、0.04 mm、0.27 mm,随机影响对EW方向的影响最大,NS方向次之,垂直方向的影响最小,可为参考框架更新提供依据。
4) 水平方向上,逐年缩短的基线主要分布在北东方向,在N分量中尤为明显; L分量中逐年缩短的基线主要集中在北东与北西方向,在近海和内陆地区都有较明显的分布。
本文虽考虑了共模误差的非线性影响,但未考虑由地表大气压强、非潮汐海洋、积雪深度、土壤湿度等地表质量负荷和温度引起的测站位移,对构建区域速度场模型及mm级参考框架均有一定的影响,未来还需进一步研究。
| [1] |
Altamimi Z, Rebischung P, Métivier L, et al. ITRF2014: A New Release of the International Terrestrial Reference Frame Modeling Nonlinear Station Motions[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(8): 6 109-6 131 DOI:10.1002/2016JB013098
(  0) 0) |
| [2] |
王伟. 中国大陆现今地壳运动的GPS分析与构造变形模拟[D]. 北京: 中国地震局地球物理研究所, 2013 (Wang Wei. Study on Present-Day Crustal Movement with GPS Data and Modeling the Active Deformation in the Chinese Mainland[D]. Beijing: Institute of Geophysics, CEA, 2013)
(  0) 0) |
| [3] |
马下平, 赵立都. 陆态网络GNSS基准站地壳运动速度场分析[J]. 测绘科学, 2018, 43(8): 1-6 (Ma Xiaping, Zhao Lidu. Analysis of Crustal Movement Velocity Field Based on GNSS Base Stations in CMONOC[J]. Science of Surveying and Mapping, 2018, 43(8): 1-6)
(  0) 0) |
| [4] |
蒋志浩. CGCS2000参考框架维持、更新理论与方法研究[J]. 测绘学报, 2019, 48(12): 1 636 (Jiang Zhihao. Research on the Theory and Method of Maintenance and Renewal of CGCS2000 Reference Frame[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(12): 1 636)
(  0) 0) |
| [5] |
蒋志浩, 张鹏, 秘金钟, 等. 基于非线性运动分析的CGCS2000下我国CORS站运动特征[J]. 地球物理学报, 2012, 55(3): 841-850 (Jiang Zhihao, Zhang Peng, Bei Jinzhong, et al. Characteristics of the Non-Linear Movement of CORS Network in China Based on the CGCS2000 Frame[J]. Chinese Journal of Geophysics, 2012, 55(3): 841-850 DOI:10.6038/j.issn.0001-5733.2012.03.014)
(  0) 0) |
| [6] |
Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego: University of California, 2002
(  0) 0) |
| [7] |
Montillet J P, Williams S D P, Koulali A, et al. Estimation of Offsets in GPS Time-Series and Application to the Detection of Earthquake Deformation in the Far-Field[J]. Geophysical Journal International, 2015, 200(2): 1 207-1 221 DOI:10.1093/gji/ggu473
(  0) 0) |
| [8] |
Langbein J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada[J]. Journal of Geophysical Research Atmospheres, 2008, 113(B5)
(  0) 0) |
| [9] |
Li W D, Jiang W P, Li Z, et al. Extracting Common Mode Errors of Regional GNSS Position Time Series in the Presence of Missing Data by Variational Bayesian Principal Component Analysis[J]. Sensors, 2020, 20(8): 2 298 DOI:10.3390/s20082298
(  0) 0) |
| [10] |
许昌. IGS站点坐标时间序列噪声特性与季节性变化分析[J]. 测绘学报, 2019, 48(4): 535 (Xu Chang. Noise Characteristics and Seasonal Variations of IGS Site Coordinate Time Series[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(4): 535)
(  0) 0) |
| [11] |
郭南男, 赵静旸. 一种改进的GPS区域叠加滤波算法[J]. 武汉大学学报: 信息科学版, 2019, 44(8): 1 220-1 225 (Guo Nannan, Zhao Jingyang. An Improved Stacking Filtering Algorithm for GPS Network[J]. Geomatics and Information Science of Wuhan University, 2019, 44(8): 1 220-1 225)
(  0) 0) |
2. Geodetic Data Processing Center, MNR, 334 East-Youyi Road, Xi'an 710054, China
 2021, Vol. 41
2021, Vol. 41

