2. 南方海洋科学与工程广东省实验室(珠海),广东省珠海市港湾1号,519080;
3. 中国地震局地质研究所地震动力学国家重点实验室,北京市华严里甲1号,100029
岩石圈有效弹性厚度(Te)是指与岩石圈板块中实际应力产生的弯矩相等的理论弯曲弹性薄板的厚度[1-2],是一个描述岩石圈在地质时间尺度下的强度指标[3],对于探讨岩石圈的动力学模型和构造运动有重要作用,通常通过重力异常和地形在频域中的相关性计算得到[4]。20世纪90年代之前,研究者利用互相独立的船载重力观测和船载地形观测数据计算有效弹性厚度[5-6],但鉴于船测资料往往与测线的选择密切相关,其反映的仅是测线段上的有效弹性厚度值。随着卫星技术的发展,人们可以在全球进行地形和重力观测,从而计算大区域和全球尺度的岩石圈弹性厚度,不过测高卫星资料常被同时应用于全球地形模型和全球重力场模型中[7-8],可能会对地形和重力的相关性产生影响,从而影响有效弹性厚度的估计。
考虑到在张裂构造背景下构造单元的变形程度与岩石圈强度密切相关[9],计算南海地区的有效弹性厚度能进一步了解整个区域的岩石圈强度,并有助于理解该区域的构造演化过程。本文以南海地区南沙群岛为例,分析测高卫星资料对计算有效弹性厚度的影响,并计算南海地区有效弹性厚度的分布,结合岩石圈年龄分析计算结果的含义。
1 计算方法与数据 1.1 岩石圈Te计算基本原理岩石圈有效弹性厚度的计算通常采用导纳法和相关性法等谱分析方法,在海洋区域一般采用导纳法[10]。该方法对重力异常和海底地形进行谱分析,计算两者之间的导纳关系,即实测导纳Z,将计算结果与岩石圈Te取不同值时根据模型计算得到的理论导纳Z′进行比较,当两者之差的均方根最小时获得Te的计算结果。
岩石圈Te由挠曲均衡理论确定[3],具体计算原理见文献[11]。可以看出,导纳法计算Te需要重力、地形及地壳结构等信息。
1.2 计算南沙群岛Te的数据及参数设置南海地区(10°S~30°N,90°E~130°E)重力观测资料丰富,有不少学者利用各种方法和资料计算了南沙群岛的有效弹性厚度[12-14],但普遍没有考虑测高卫星对数据资料的影响。作为构造活动相对稳定的区域,在计算Te时可将南海地区作为一般的加载模型,根据前人经验,这种条件适合采用导纳法进行Te计算[15]。
为对比测高卫星资料的影响,分别采用由测高卫星资料和重力资料联合得到的重力场模型(WGM2012)[16]及完全由重力卫星得到的重力场模型(ITU_GGC16)[17]计算Te,计算所需的地形模型选择由船测资料和测高卫星共同得到的GEBCO模型[18]。本文重力模型在南海地区的重力异常和地形如图 1所示,可以发现,地形与重力异常存在对应关系,越陡峭的区域重力异常越显著,这是一般加载模型的典型特征。
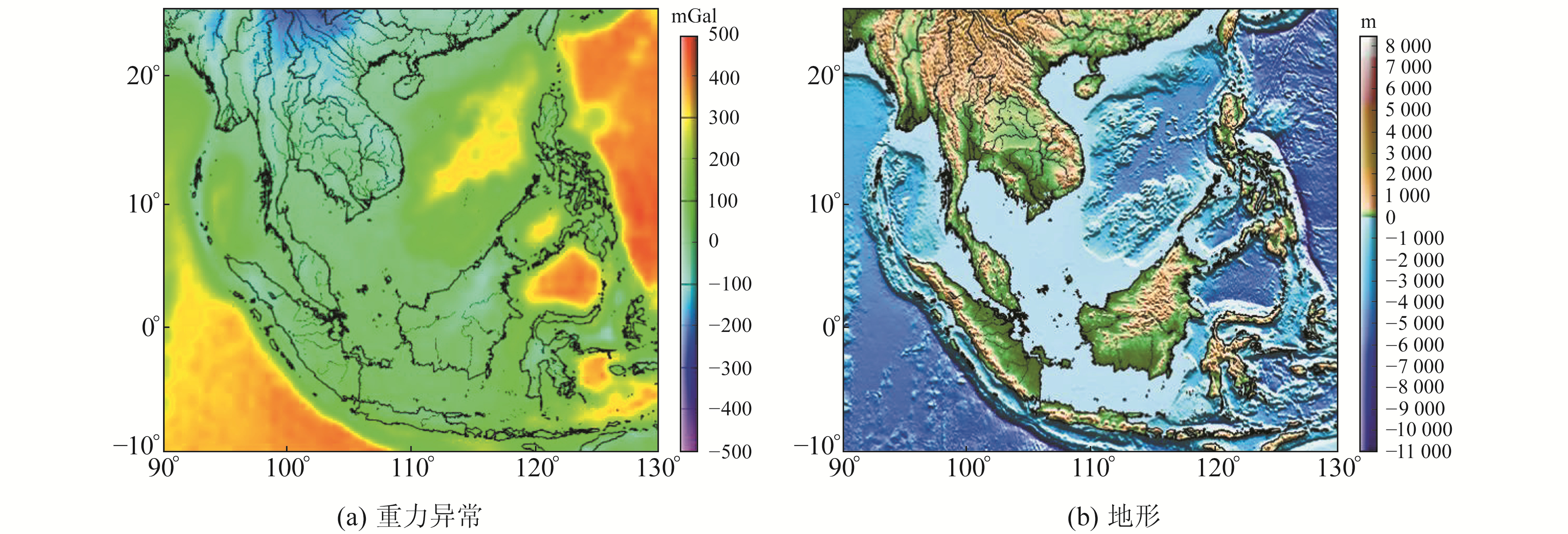
|
图 1 南海地区的重力异常和地形 Fig. 1 The gravity anomaly and the topography in the South China Sea |
Clift等[19]在南沙群岛(8°N~13°N,111°E~116°E)附近使用地质模拟方法来估算岩石圈的Te,其基本思路是应用不同的Te正演模拟长时间以来(28 Ma)海底地貌沉积的分布与厚度,并将其与当前地震反射剖面得到的地壳结构作对比,估算得到南沙群岛的Te值为8~10 km。考虑到该方法与本文计算Te的思路完全不同,可以作为一个互相印证的指标。
在计算研究有效弹性厚度时还需涉及该区域的地壳模型参数,包括地壳分层厚度、每层密度、杨氏模量及泊松比等。为此,选择现有分辨率最高(1°×1°)的全球地壳模型crust1.0模型[20]作为这些参数的来源(表 1),其中海水、地壳和地幔密度分别为模型在研究区域的平均值,平均水深为模型提供的平均值。
|
|
表 1 研究区域的部分地壳参数 Tab. 1 The crustal parameters of the study area |
首先计算南沙群岛的Te(图 2),并与前人研究成果[12-14, 19, 21-22]进行对比(表 2)。
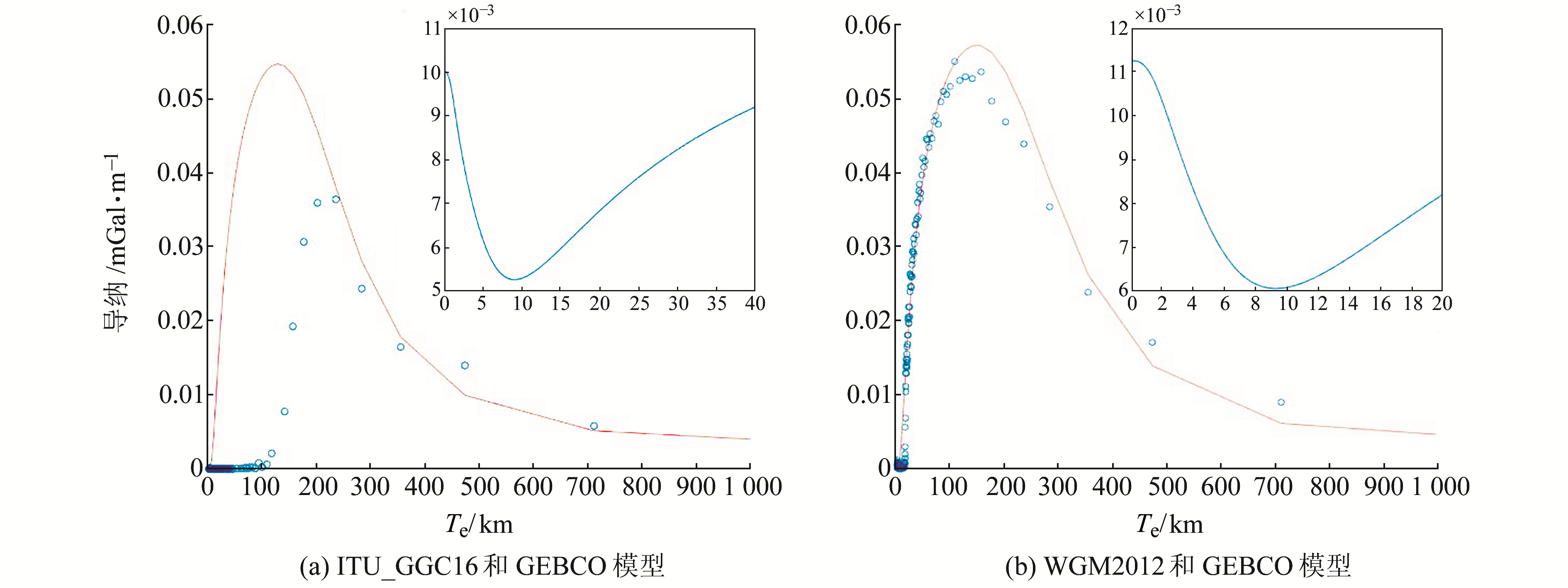
|
图 2 两种模型的最佳拟合Te及相应的RMS Fig. 2 The best fitting Te of two models and their RMS |
|
|
表 2 南沙群岛Te研究对比 Tab. 2 Comparison of different studies of Te in Nansha islands |
通过拟合发现,南沙群岛地区利用ITU_GGC16模型计算时的最佳Te为9.1 km,最佳拟合时的均方根为5.3 mGal/km(图 2(a));利用WGM2012模型拟合时的最佳Te为9.3 km,最佳拟合时的均方根为6.1 mGal/km(图 2(b))。采用联合的重力场模型比采用重力卫星的重力场模型计算的Te要高约2%;而采用2种数据计算的最小均方根在5~6 mGal/km,两者的拟合情况都比较好。需要说明的是,由于ITU_GGC16模型受空间分辨率的限制,仅使用波长在250~1 000 km的部分进行拟合。考虑到采用WGM2012模型可能会高估有效弹性厚度,本文认为利用ITU_GGC16模型计算得到的Te比利用WGM2012模型计算得到的Te更准确。
与前人的计算结果对比发现,南沙群岛Te的计算结果有一定的差异,即使使用同类方法,因为应用的算法参数和采用的数据及地壳模型不同,结果也存在一定差距。总体来看,除了Tesauro等[22]的结果,其他研究的Te值都在4~20 km的区间范围内,其中同样应用导纳法计算Te的苏达权[12]采用的海底地形模型(Sandwell模型)由测高卫星反演得到,应用相关性法的Shi等[13]采用的模型组合与本文的WGM2012+GEBCO组合类似,也存在重力模型与地形模型不互相独立的问题,其结果都比本文结果稍高,可能高估了实际的有效弹性厚度。考虑到Clift等[19]采用的地质模拟法与本文方法在数据和思路上均不相同,但结果较为接近,证明本文计算结果比较可靠。
总体来看,在南沙群岛地区计算有效弹性厚度时重力模型是否包含测高卫星资料对计算结果存在一定的影响,测高卫星资料未重复应用在重力模型和地形模型中的计算结果要小于重复应用的情况。
2.2 南海Te分布计算和分析进一步计算南海地区(图 3(a))的Te分布,计算时采用多窗口法[23-24],选择一个800 km×800 km的滑动窗口,并以50 km的间隔滑动,最后平滑得到1°×1°的有效弹性厚度分布。§2.1的结果表明,在计算有效弹性厚度时,如果在重力模型和地形模型中重复使用测高卫星资料可能高估该值,所以在计算Te分布时采用GEBCO地形模型,重力模型采用不包含测高卫星资料的ITU_GGC16模型。为减少干扰,去掉陆地部分的有效弹性厚度结果,仅看海洋部分,将南海海盆地区(0°~25°N,95°E~125°E)作为分析重点并放大(图 3(b))。
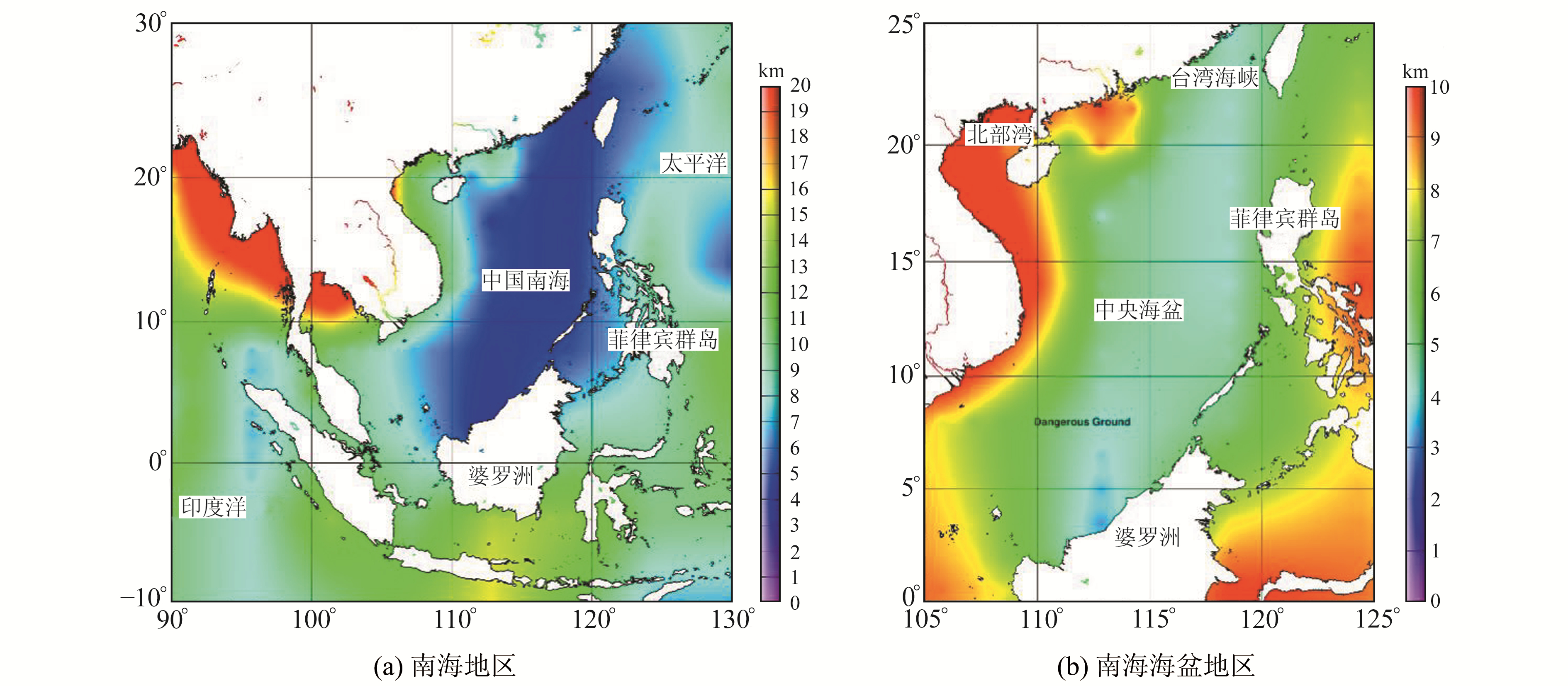
|
图 3 有效弹性厚度分布 Fig. 3 The Te distribution |
可以看出,南海地区的Te值显著低于周边区域,基本在3~8 km的区间范围,而南海中央海盆地区的Te值约为4 km,相比之下南海周缘的Te值稍大。东北部台湾海峡附近和靠近菲律宾群岛处均为7 km左右,中央海盆西侧的Te值从7 km一直上升到北部湾地区的10 km。南部靠近婆罗洲地区存在Te值锐减至4 km的区域,但在南海之外的地区Te值整体较大,东侧的菲律宾海沟处Te值为10~15 km,南侧越过婆罗洲的区域能达到16 km,这也是除了印度洋除靠近青藏高原的部分外Te值最大的区域。
根据全球岩石圈年龄模型[25](图 4)对比南海地区的岩石圈Te可以发现,最小Te的南海海盆对应着最年轻的岩石圈,符合南海海盆的扩张历史;印度洋北部和印尼地区有较大的Te,对应岩石圈相对古老的年龄。菲律宾海沟的西侧为Te较小的区域,而海沟东侧的Te显著增大,这也与岩石圈的年龄相对应。总体来看,在海洋或者洋壳区域,有效弹性厚度的分布与岩石圈年龄的分布比较一致。
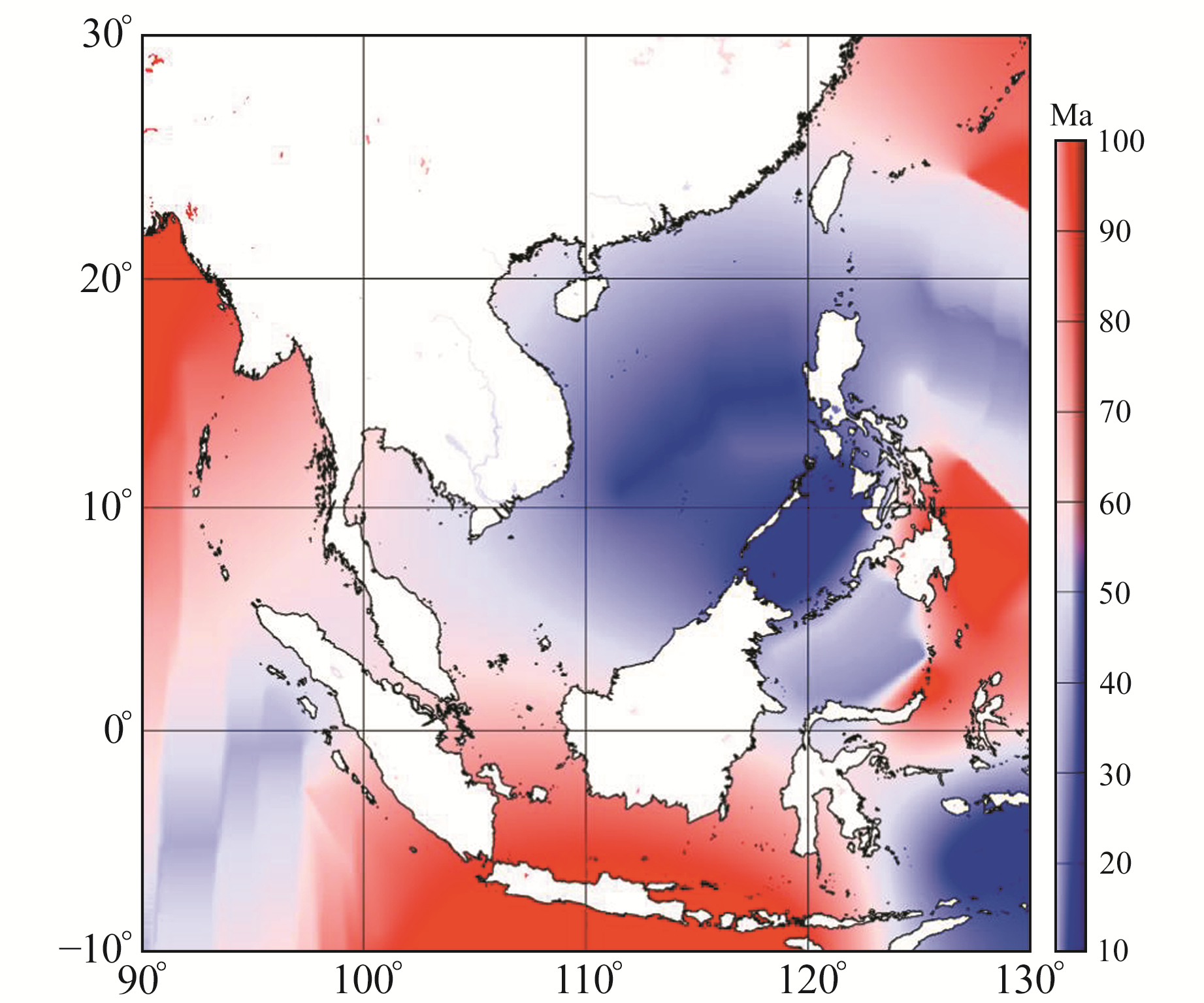
|
图 4 南海地区岩石圈年龄分布 Fig. 4 The lithosphere age distribution in the South China Sea |
本文利用2种不同的数据组合计算了南海地区南沙群岛的岩石圈有效弹性厚度,分析了重力模型及地形模型均来自卫星测高数据时对计算结果的影响,同时计算了南海地区的有效弹性厚度分布,并与南海地区的岩石圈年龄进行对比,通过对计算结果的分析得出以下结论:
1) 在计算有效弹性厚度时,如果重力模型和地形模型都应用了测高卫星资料,会导致重力模型和地形模型不互相独立,从而高估有效弹性厚度值,在南沙群岛地区的高估影响约为2%。
2) 虽然ITU_GGC16重力模型的空间分辨率低于WGM2012模型,但由于有效弹性厚度反映的是长波段的岩石圈信息,ITU_GGC16重力模型的波段能够有效覆盖从而得到准确的有效弹性厚度值。
3) 对比前人计算得到的南沙群岛有效弹性厚度值,本文得到的约9 km的结果与同类方法的结果相近,与思路不同的地质模拟法的计算结果也比较接近,所以认为9 km的有效弹性厚度值结果是可信的。
4) 南海地区岩石圈的有效弹性厚度分布表明,南海地区有效弹性厚度在0~15 km之间,南海海盆的有效弹性厚度最小(可以达到4 km),北部湾地区的有效弹性厚度相对较大(可以超过10 km)。总体来看,南海周边区域的有效弹性厚度值普遍比南海地区大,印尼周边区域、印度洋北部和菲律宾海沟东部部分地区存在较大的有效弹性厚度,能达到10~20 km。
5) 南海地区的有效弹性厚度与海底岩石圈年龄的空间分布有较强的相关性,这与前人的研究结论一致。南海海盆的有效弹性厚度小于周缘地区的有效弹性厚度,这也符合南海海盆的扩张历史。
| [1] |
Forsyth D W. Subsurface Loading and Estimates of the Flexural Rigidity of Continental Lithosphere[J]. Journal of Geophysical Research, 1985, 90(B14): 12 623-12 632 DOI:10.1029/JB090iB14p12623
(  0) 0) |
| [2] |
付永涛, 李安春, 秦蕴珊. 大洋和大陆边缘岩石圈有效弹性厚度的研究意义[J]. 海洋地质与第四纪地质, 2002, 22(3): 69-75 (Fu Yongtao, Li Anchun, Qin Yunshan. Effective Elastic Thickness of the Oceanic and Continental Marginal Lithospheres[J]. Marine Geology and Quaternary Geology, 2002, 22(3): 69-75)
(  0) 0) |
| [3] |
Watts A B. Isostasy and Flexure of the Lithosphere[M]. Cambridge: Cambridge University Press, 2001
(  0) 0) |
| [4] |
Kirby J F. Estimation of the Effective Elastic Thickness of the Lithosphere Using Inverse Spectral Methods: The State of the Art[J]. Tectonophysics, 2014, 631: 87-116 DOI:10.1016/j.tecto.2014.04.021
(  0) 0) |
| [5] |
Mckenzie D, Bowin C. The Relationship between Bathymetry and Gravity in the Atlantic Ocean[J]. Journal of Geophysical Research, 1976, 81(11): 1 903-1 915 DOI:10.1029/JB081i011p01903
(  0) 0) |
| [6] |
Watts A B, McKenzie D P, Parsons B E, et al. The Relationship between Gravity and Bathymetry in the Pacific Ocean[J]. Geophysical Journal International, 1985, 83(1): 263-298 DOI:10.1111/j.1365-246X.1985.tb05166.x
(  0) 0) |
| [7] |
Leuliette E W, Miller L. Closing the Sea Level Rise Budget with Altimetry, Argo, and GRACE[J]. Geophysical Research Letters, 2009, 36(4)
(  0) 0) |
| [8] |
Chen J L, Wilson C R, Tapley B D, et al. Long-Term and Seasonal Caspian Sea Level Change from Satellite Gravity and Altimeter Measurements[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(3): 2 274-2 290
(  0) 0) |
| [9] |
吴保珍, 施小斌, 杨小秋, 等. 南海北部白云凹陷及其邻区的岩石圈强度分析[J]. 热带海洋学报, 2014(1): 62-68 (Wu Baozhen, Shi Xiaobin, Yang Xiaoqiu, et al. Analysis on Lithospheric Strength of the Baiyun Sag and Its Surrounding Area in the Northern Margin of the South China Sea[J]. Journal of Tropical Oceanography, 2014(1): 62-68 DOI:10.3969/j.issn.1009-5470.2014.01.008)
(  0) 0) |
| [10] |
Simons F J, Olhede S C. Maximum-Likelihood Estimation of Lithospheric Flexural Rigidity, Initial-Loading Fraction and Load Correlation, under Isotropy[J]. Geophysical Journal International, 2013, 193(3): 1 300-1 342 DOI:10.1093/gji/ggt056
(  0) 0) |
| [11] |
胡敏章, 李建成, 李辉, 等. 西北太平洋岩石圈有效弹性厚度及其构造意义[J]. 地球物理学报, 2015, 58(2): 542-555 (Hu Minzhang, Li Jiancheng, Li Hui, et al. The Lithosphere Effective Elastic Thickness and Its Tectonic Implications in the Northwestern Pacific[J]. Chinese Journal of Geophysics, 2015, 58(2): 542-555)
(  0) 0) |
| [12] |
苏达权. 海洋岩石圈板块有效弹性厚度研究[J]. 地球物理学报, 2012, 55(10): 3 259-3 265 (Su Daquan. A Study of the Effective Elastic Thickness of the Oceanic Lithosphere[J]. Chinese Journal of Geophysics, 2012, 55(10): 3 259-3 265)
(  0) 0) |
| [13] |
Shi X B, Kirby J, Yu C H, et al. Spatial Variations in the Effective Elastic Thickness of the Lithosphere in Southeast Asia[J]. Gondwana Research, 2017, 42: 49-62 DOI:10.1016/j.gr.2016.10.005
(  0) 0) |
| [14] |
胡敏章, 李建成, 徐新禹, 等. 全球1°×1°海洋岩石圈有效弹性厚度模型[J]. 武汉大学学报: 信息科学版, 2017, 42(5): 575-582 (Hu Minzhang, Li Jiancheng, Xu Xinyu, et al. A 1°×1° Model for Lithospheric Effective Elastic Thickness over Global Seafloor[J]. Geomatics and Information Science of Wuhan University, 2017, 42(5): 575-582)
(  0) 0) |
| [15] |
Kalnins L M, Watts A B. Spatial Variations in Effective Elastic Thickness in the Western Pacific Ocean and Their Implications for Mesozoic Volcanism[J]. Earth and Planetary Science Letters, 2009, 286(1-2): 89-100 DOI:10.1016/j.epsl.2009.06.018
(  0) 0) |
| [16] |
Bonvalot S, Balmino G, Briais A, et al. World Gravity Map[EB/OL]. https://bgi.obs-mip.fr/data-products/grids-and-models/recent-gravity-maps/, 2012
(  0) 0) |
| [17] |
Akyilmaz O, Ustun A, Aydin C, et al. ITU_GGC16 the Combined Global Gravity Field Model Including GRACE & GOCE Data up to Degree and Order 280[EB/OL]. https://doi.org/10.5880/icgem.2016.005, 2016
(  0) 0) |
| [18] |
Weatherall P, Marks K M, Jakobsson M, et al. A New Digital Bathymetric Model of the World's Oceans[J]. Earth and Space Science, 2015, 2(8): 331-345 DOI:10.1002/2015EA000107
(  0) 0) |
| [19] |
Clift P, Lin J, Barckhausen U. Evidence of Low Flexural Rigidity and Low Viscosity Lower Continental Crust during Continental Break-up in the South China Sea[J]. Marine and Petroleum Geology, 2002, 19(8): 951-970 DOI:10.1016/S0264-8172(02)00108-3
(  0) 0) |
| [20] |
Laske G, Masters G, Ma Z T, et al. Update on CRUST1. 0— A 1-Degree Global Model of Earth's Crust[C]. EGU General Assembly, Vienna, 2013
(  0) 0) |
| [21] |
Braitenberg C, Wienecke S, Wang Y. Basement Structures from Satellite-Derived Gravity Field: South China Sea Ridge[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B5)
(  0) 0) |
| [22] |
Tesauro M, Kaban M K, Cloetingh S A P L. Global Model for the Lithospheric Strength and Effective Elastic Thickness[J]. Tectonophysics, 2013, 602: 78-86 DOI:10.1016/j.tecto.2013.01.006
(  0) 0) |
| [23] |
Deng Y F, Zhang Z J, Fan W M, et al. Multitaper Spectral Method to Estimate the Elastic Thickness of South China: Implications for Intracontinental Deformation[J]. Geoscience Frontiers, 2014, 5(2): 193-203 DOI:10.1016/j.gsf.2013.05.002
(  0) 0) |
| [24] |
Audet P. Toward Mapping the Effective Elastic Thickness of Planetary Lithospheres from a Spherical Wavelet Analysis of Gravity and Topography[J]. Physics of the Earth and Planetary Interiors, 2014, 226: 48-82 DOI:10.1016/j.pepi.2013.09.011
(  0) 0) |
| [25] |
Müller R D, Sdrolias M, Gaina C, et al. Age, Spreading Rates, and Spreading Asymmetry of the World's Ocean Crust[J]. Geochemistry, Geophysics, Geosystems, 2008, 9(4)
(  0) 0) |
2. Southern Marine Science and Engineering Guangdong Laboratory(Zhuhai), 1 Gangwan, Zhuhai 519080, China;
3. State Key Laboratory of Earthquake Dynamics, Institute of Geology, CEA, A1 Huayanli, Beijing 100029, China
 2021, Vol. 41
2021, Vol. 41

