2. 华北理工大学矿业工程学院,河北省唐山市建设南路80号,063210
PSInSAR技术通过分析SAR影像序列中的时间稳定永久散射体(permanent scatterer, PS)进行地表形变监测,广泛应用于城区、滑坡等形变监测及高程修正[1-2]领域。但非城区中稀疏的稳定散射体导致在地表监测过程中PS点分布密度不足,难以精确估计速率及残差等信息,从而使PSInSAR技术在非城区地形监测应用中受限[3]。为提高非城区PS点的分布密度,相邻影像连续干涉对[4-5]、小尺寸PS点结合角反射器优化PS点分布[6]、残差估计与解缠绕模型优化提高空间相干PS点识别率[7]、多尺度频率自适应相干估计提高PS点识别[8]等提高PS点分布密度的改进算法被相继提出。
在已有研究基础上,为解决非城区PS点分布不足而导致PSInSAR技术在非城区地表形变监测误差较大的问题,提出基于分时散射体(partial time scatterer, PTS)的改进PSInSAR算法。首先对SAR影像进行基于改进经验模态分解(empirical mode decomposition, EMD)算法的滤波降噪,然后采用双阈值与可信概率估计进行PTS提取,最后通过参数差分迭代估计法对PTS目标进行相位分离和形变速率估计,从而得到非城区监测区的地表形变。
1 边缘保持平滑滤波在经典PSInSAR算法的SAR影像干涉对(i, k)中,像元P的邻域像素具有平稳随机过程特性[9],因此其相干系数可表示为:
| $ \gamma_{P}^{i, k}=\frac{\sum\limits_{n=1}^{W} S_{i}^{(n)} S_{k}^{(n)}}{\sqrt{\sum\limits_{n=1}^{W}\left|S_{i}^{(n)}\right|^{2} \sum\limits_{n=1}^{W}\left|S_{i}^{*(n)}\right|^{2}}} $ | (1) |
式中,Si(n)和Sk(n)分别为影像对中影像i和影像k的局部信息块,*为复共轭运算。根据预设阈值T,γPi, k可将地表散射体划分为高相干PS、部分时序高相干PTS及低相干目标3类,由于非城区内PS数量较少,不足以保证经典算法的监测精度,而非城区可能存在大量部分时序高相干性的分时散射体目标,因此本文将PTS目标引入到经典PSInSAR算法中,以提高其在非城区地表形变监测中的精确率和适应性[10]。
SAR影像中通常含有较多的干扰噪声,因此在PTS目标提取前需对SAR影像进行滤波降噪。将传统EMD算法直接应用于SAR影像时,易造成对SAR影像边缘区域像素值的过度滤波[5],并且其模式混叠及以经验为依据的分量识别会使重建信号的准确度较低。为此,在传统算法行列分解的基础上,引入45°和135°两个分解方向,同时为优化IMF分量分界时相关系数法的复杂性和单一指标的不确定性,本文联合SAR影像的细节信息与逼近信息,采用基于均方根R和平滑度r估计的IMF分界K值自适应定位方法。假设干涉图经过改进EMD处理后的分量为dj(x),等权滤波并重构后可得:
| $ \begin{array}{c} \bar{d}_{j}^{V}(x)=\frac{1}{f_{\text {imf }}(x)} \sum\limits_{q=1}^{h} \sum\limits_{z=-1}^{+1} \omega^{(t)}(x+z) f_{\operatorname{imf}_{j, q}}^{t}(x)+ \\ \sum\limits_{q=h+1}^{n} f_{\operatorname{imf}_{j, q}}(x)+r_{j}^{V} \end{array} $ | (2) |
式中,z和ω(x)分别为平滑滤波器的系数及窗口值。R和r的表达式为:
| $ R =\sqrt{\sum\limits_{t=0}^{N-1}\left(I_{\mathrm{imf}}(t)-x(t)^{2}\right) / N} $ | (3) |
| $ r =\frac{\sum\limits_{t=0}^{N-2}\left(I_{\mathrm{imf}}(t+1)-I_{\mathrm{imf}}(t)\right)^{2}}{\sum\limits_{t=0}^{N-2}(x(t+1)-x(t))^{2}} $ | (4) |
式中,x(t)为含噪SAR干涉对影像序列。归一化R和r,并由变异系数法进行赋权处理,即
| $ \left\{\begin{array}{l} W_{R}=\frac{\sigma_{R} / \mu_{R}}{\sigma_{R} / \mu_{R}+\sigma_{r} / \mu_{r}} \\ W_{r}=\frac{\sigma_{r} / \mu_{r}}{\sigma_{R} / \mu_{R}+\sigma_{r} / \mu_{r}} \end{array}\right. $ | (5) |
式中,μ和σ为相应的均值与标准差。由此可得,IMF分界的复合指标为Fo=WR×PR+Wr×Pr,相应的分界阈值为:
| $ T_{k-1}=\left|F_{o}(k-1) / F_{o}(k)\right| $ | (6) |
则滤波时的约束权系数ω(x)为:
| $ \omega(x)=\exp \left[-\left|{f^{\prime}}_{\text {imf }}(x)\right| /\left(2 \eta^{2}\right)\right] $ | (7) |
式中,f′imf(u)为一阶导数;η用于判断像素的边缘归属,当像元η值大于梯度时,则划归为非边缘,反之则划归为边缘。当首次出现Tk-1∈[1, 3]时,则分界值K=k-1,此时将序号k之前的IMF分量划归为噪声,对序号k之后的IMF分量进行重构,可得到去噪后的SAR干涉影像对。
2 PTS目标提取对SAR影像干涉图进行边缘保持滤波后,首先由离差指数和相干系数对PTS目标点进行联合初识,获得PTS的候选目标[9],以缩小后续目标点的搜索范围,然后由目标点的相位信息推导其可信概率作为PTS可靠筛选的依据。
差分干涉图上某像元位置PTS候选目标的差分相位φint, lg由地表形变相位φdef, lg、大气相位φatm, lg、噪声相位φnoi, lg和地形相位残差Δφε, lg组成,其中l和g分别为干涉图序号及其像元位置。
已有研究表明[10],Δφε, lg具有一定范围内的空间相关性,而φdef, lg、φatm, lg在视线向(LOS)具有空间相关性,因此残余相位可表示为:
| $ W\left\{\varphi_{\mathrm{int}, l}^{g}-\hat{\varphi}_{\mathrm{int}, l}^{g}\right\}=W\left\{\Delta \varphi_{\varepsilon, l}^{\mathrm{nc}, g}+\varphi_{\mathrm{noi}, l}^{\mathrm{nc}, g}+\delta_{l}^{g}\right\} $ | (8) |
式中,φnc为差分相位的非相关部分,δlg为一个可忽略的较小值。Δφε, lnc, g的表达式为:
| $ \Delta \varphi _{\varepsilon ,l}^{{\rm{nc}},g} = \frac{{{\rm{4 \mathsf{ π} }}}}{{\lambda \bar R\sin \bar \theta }}B_{ \bot ,l}^g\Delta \varepsilon + \frac{{{\rm{4 \mathsf{ π} }}}}{\lambda }{T_i}\Delta v + \Delta \theta _l^{{\rm{nc}},g} $ | (9) |
式中,θ为入射角,λ为波长,R和θ为参数均值,B⊥, lg为时间基线,Δε和Δv为高程残差增量和形变速率增量,Δθlnc, g为残留的相位增量。采用最优化方法[2]对式(9)进行求解,可通过构建观测方程估计相关增量值,进而构建相干系数的目标函数:
| $ {r_g} = \frac{1}{{N - 1}}\left| {\sum\limits_{l - 1}^{N - 1} {\left( {\cos \Delta \omega _l^g + {\rm{j}}\sin \Delta \omega _l^g} \right)} } \right| $ | (10) |
式中,Δω为观测值与拟合值的相位差,即
| $ \Delta {\omega _i} = \Delta {\varphi _i} - \frac{{{\rm{4 \mathsf{ π} }}}}{{\lambda \bar R\sin \bar \theta }}B_{ \bot ,i}^g\Delta \varepsilon - \frac{{{\rm{4 \mathsf{ π} }}}}{\lambda }{T_i}\Delta v $ | (11) |
进而可得候选目标为可靠PTS的概率为:
| $ P_{g}=1-\left[(1-\alpha) p_{R}\left(r_{g}\right) / p\left(r_{g}\right)\right] $ | (12) |
式中,p(·)与pR(·)分别为PTS像元与非PTS像元的概率函数,α为调节系数。
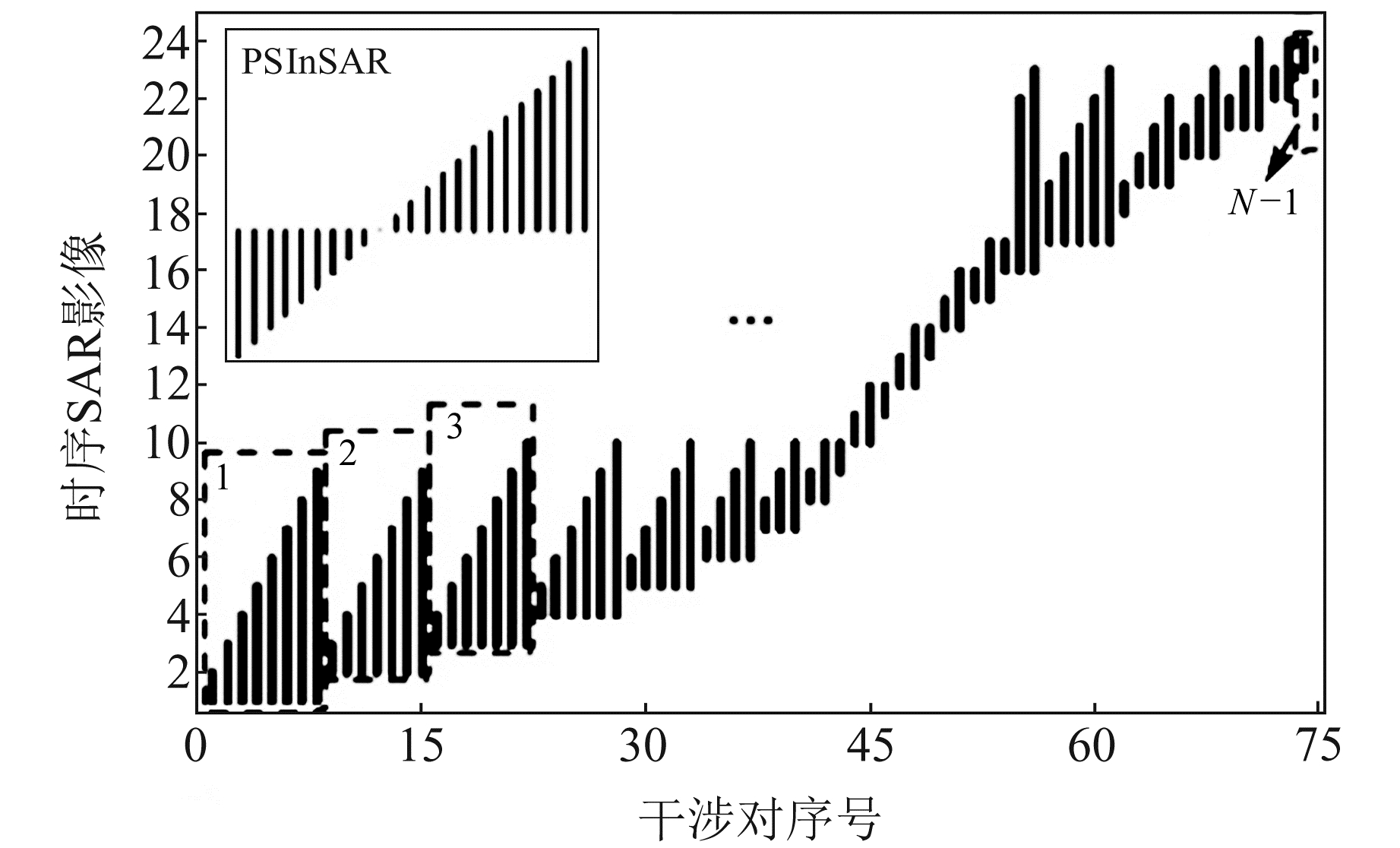
3 基于PTS的PSInSAR监测根据大气自相关特性对由提取的PTS目标构建的Delaunay三角网进行二次差分,并建立三角网连接边上像元的观测方程[8]。在提取PTS目标点时,由于PTS目标的季节、气象等的分时稳定性是主要参考因素,传统的基于共同主影像PSInSAR算法的参数解算过程在解析PTS贡献时较为困难,因此借助连续干涉对思想[4],将干涉图聚类为N-1个具有不同时相特性的组合(图 1),并以相干度作为组内各影像贡献度的衡量权重,以削弱低相干影像的贡献。
|
图 1 影像干涉对时间基线及其分组 Fig. 1 Image interference pair time baseline and its grouping |
基于以上分析,以提取的PTS目标对时序εp进行解算,其解算模型为:
| $ \varepsilon_{p}=\frac{1}{N} \sum\limits_{i=1}^{N-1} \sum\limits_{k=i+1}^{N}\left|\gamma_{p}^{k}\right|(\cos \omega+\mathrm{j} \sin \omega) / \sum\limits_{k=i+1}^{N} \gamma_{p}^{k} $ | (13) |
对干涉对进行分组并以全时序解算εp,既可保证与相干性差值相关的相位贡献差异性,又可突出聚类分组的时序意义。根据最优理论,当|εp|取极大值时,模型的输出相位最接近观测相位,此时获得的
| $ (\Delta \hat{\delta}, \Delta \hat{v})=\arg \left\{\max \left(\left|\varepsilon_{p}\right|\right)\right\} $ | (14) |
采用经典PSInSAR算法进行初始值解缠,通过Delaunay迭代求解高程修正与形变速率,即可解算出非线性形变相位[2]。
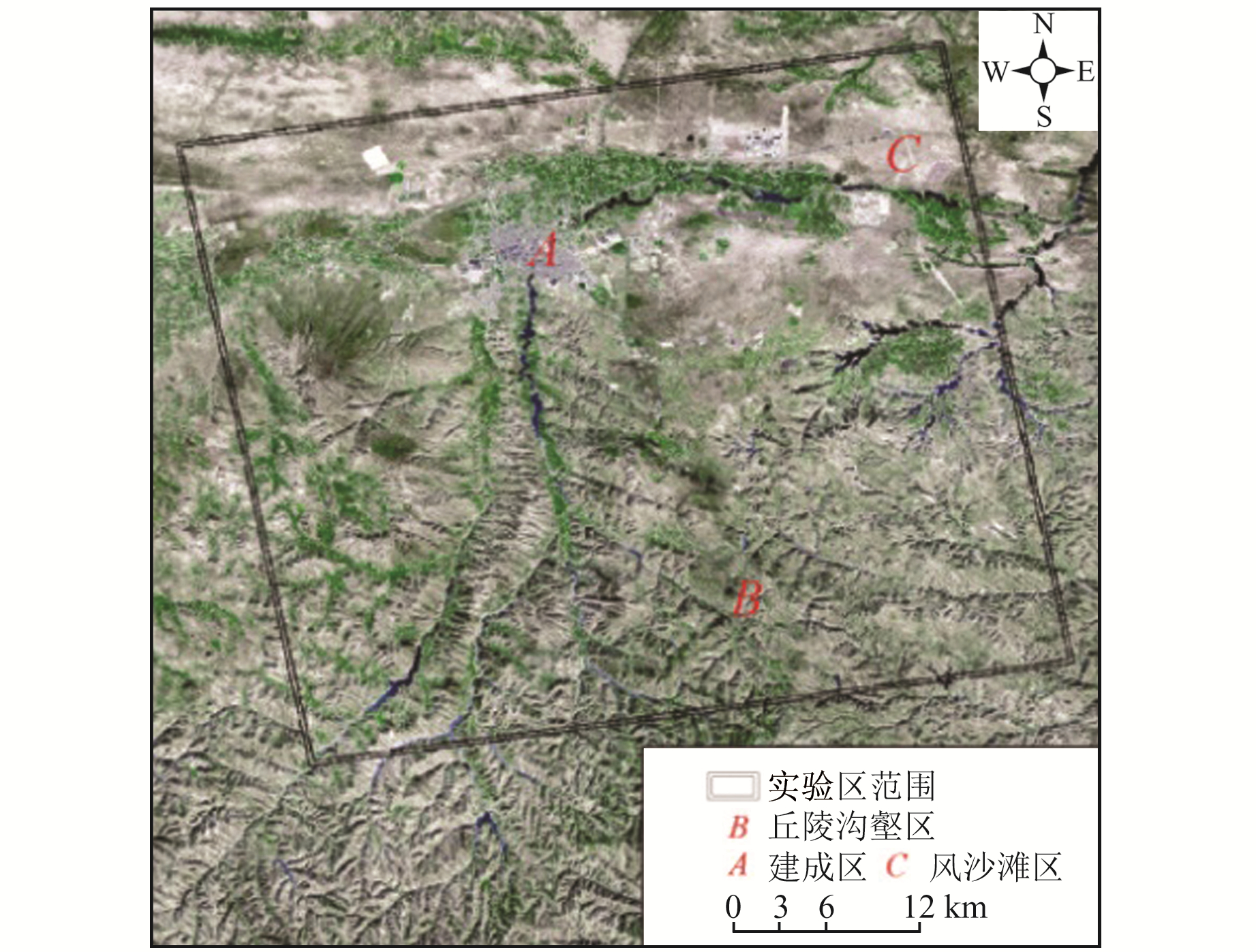
4 实验分析为验证本文算法在非城区形变监测中的有效性,以陕西靖边县周边区域作为测试实验区(图 2),实验数据为24景C波段干涉宽模式的SLC影像数据,采用ESA精密轨道数据处理配准及相关相位去除等操作。
|
图 2 实验区光学影像 Fig. 2 Optical image of the test area |
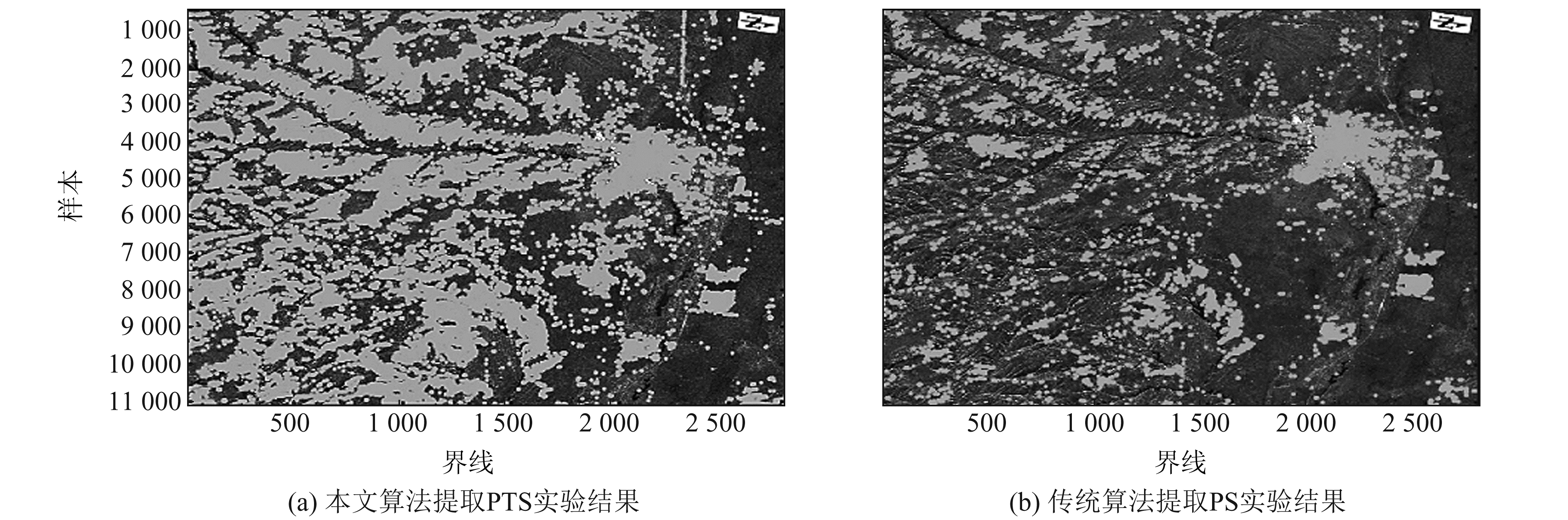
采用本文算法和传统PSInSAR算法分别提取PTS点和PS点,实验结果如图 3所示。从图中可以看出,在A区域,建筑物等可被较好地识别为PTS点和PS点;在B区域,植被较为稀少,PS点因失相干性而较少,密度较低,但本文算法仍可识别出较多的PTS点。对PTS点和PS点进行编号和经纬度重叠分析后发现,大部分传统PS点均被标记为PTS点,即这些同名的PTS点与PS点具有相同的空间分布特性,说明本文的提取算法具有有效性。
|
图 3 PTS与PS提取实验对比 Fig. 3 Comparison of PTS and PS extraction experiments |
为验证本文算法监测沉降的精度和可靠性,以实验区内2016年二等水准资料为基础,复测2016年布设的水准路线,以复测水准实际值作为精度和可靠性实验数据的基准参数,并将水准监测的垂线形变方向投影到SAR卫星LOS方向,选取与实验时间相同的水准历史资料对复测数据进行精度评价。
DSInSAR地形形变监测技术引入了雷达最新的分布式识别和滤波技术,可将裸土、沥青路面,特别是新围垦区等区域识别为DS点,因此将DSInSAR技术引入到实验中作为一种性能比较算法。提取监测区内水准点对应的形变数据点,选用平均误差
表 1(单位mm/a)为实验结果,从表中可以看出,在A区域,由于城区内永久相干目标较多,3种算法均获得了较好的误差精度;在B区域,PS点较少,形变监测精度的提高需依赖PTS点或DS点,因此本文算法和DSInSAR技术算法具有明显的优势,但本文算法更优,原因为本文算法的PTS点可充分利用测量点在不同时刻的贡献优势;在C区域,PTS点极少,沥青路面、新围垦区等具有雷达分布特性的DS点也较少,因此3种算法的监测误差均较大,而本文算法通过分时分析,在测量点较少的情况下充分利用各测量点在特征最优时刻的监测贡献度,避免监测点在特征较差时段对精度的不利影响,从而有效提高了形变监测的精度。
|
|
表 1 实验区内各算法的监测精度 Tab. 1 Monitoring accuracy of each algorithm in the experimental area |
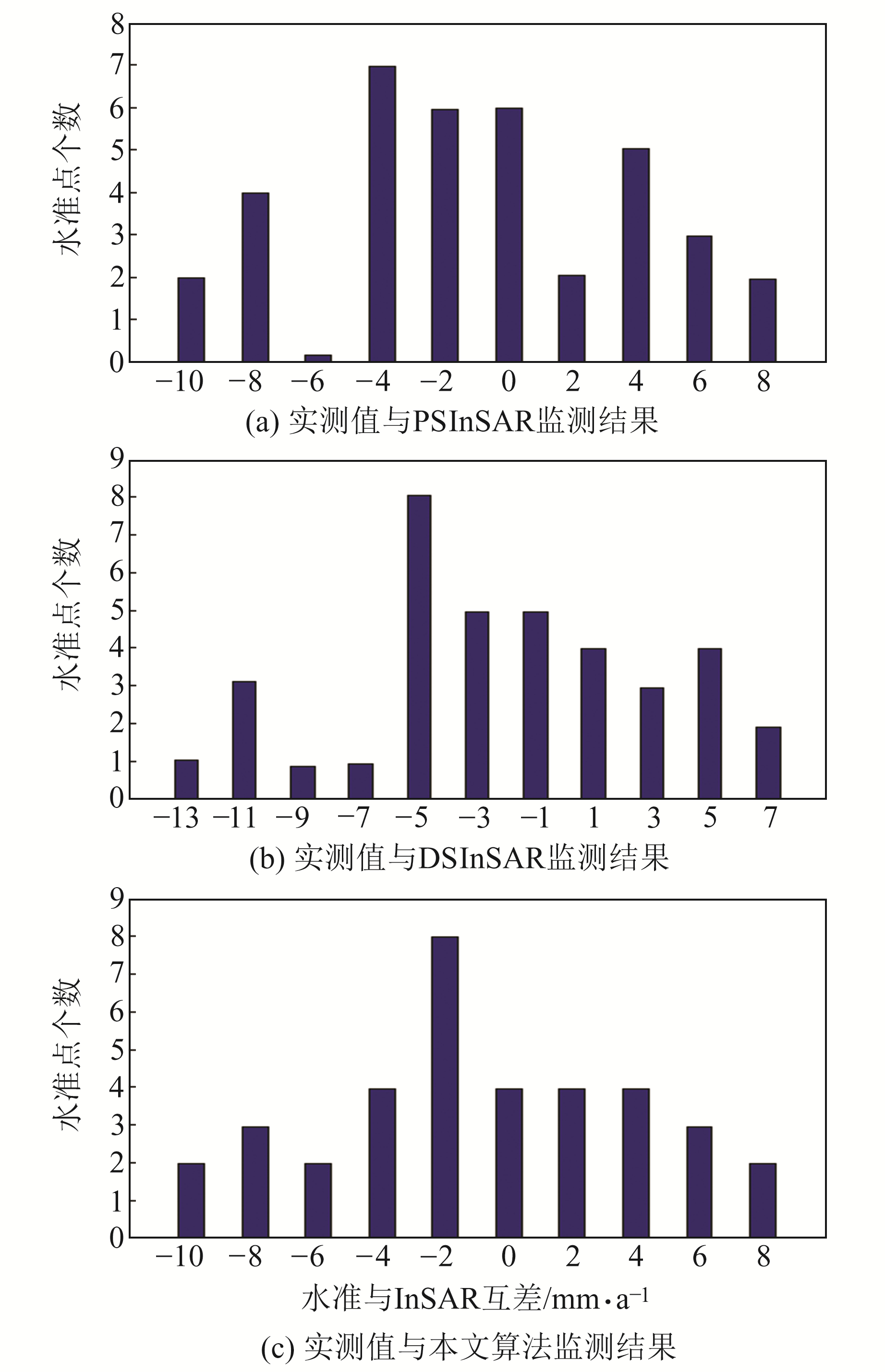
图 4为B区域水准测量结果与各算法监测结果的互差直方图,进一步验证了本文算法的监测精度较好,结果具有可靠性。
|
图 4 实测值与各算法监测结果互差直方图 Fig. 4 Histogram of mutual difference between measurement and monitoring results of each algorithm |
为解决PSInSAR技术在非城区监测误差较大的问题,提出基于PTS的改进PSInSAR算法。该算法通过改进的EMD对SAR影像进行边缘保持平滑滤波降噪,通过可信概率联合提取PTS目标;然后通过迭代估计PTS相位和形变速率,从而实现非城区地表形变的准确监测。实验结果表明,本文算法在非城区可获得比PSInSAR技术和DSInSAR技术更优的监测精度和可靠性,算法具有有效性。
| [1] |
Zhao C J, Li Z, Tian B S, et al. A Ground Surface Deformation Monitoring InSAR Method Using Improved Distributed Scatterers Phase Estimation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(11): 4 543-4 553 DOI:10.1109/JSTARS.2019.2946729
(  0) 0) |
| [2] |
周立新, 王志伟. 基于多视线向D-InSAR技术的三维地表形变抗差解算方法[J]. 大地测量与地球动力学, 2020, 40(12): 1 263-1 267 (Zhou Lixin, Wang Zhiwei. Robust Method for Resolving 3-D Surface Deformation from Multi-LOS D-InSAR Technology[J]. Journal of Geodesy and Geodynamics, 2020, 40(12): 1 263-1 267)
(  0) 0) |
| [3] |
Huang J X, Xie M W, Atkinson P M. Dynamic Susceptibility Mapping of Slow-Moving Landslides Using PSInSAR[J]. International Journal of Remote Sensing, 2020, 41(19): 7 509-7 529 DOI:10.1080/01431161.2020.1760398
(  0) 0) |
| [4] |
刘飞, 潘斌. 一种基于Sentinel-1连续干涉像对的PSInSAR算法[J]. 测绘通报, 2018(12): 30-35 (Liu Fei, Pan Bin. A New PSInSAR Algorithm Based on Sentinel-1 Consecutive Interferograms[J]. Bulletin of Surveying and Mapping, 2018(12): 30-35)
(  0) 0) |
| [5] |
鲁铁定, 钱文龙, 贺小星, 等. 一种确定分界IMF分量的改进EMD方法[J]. 大地测量与地球动力学, 2020, 40(7): 720-725 (Lu Tieding, Qian Wenlong, He Xiaoxing, et al. An Improved EMD Method for Determining Boundary IMF[J]. Journal of Geodesy and Geodynamics, 2020, 40(7): 720-725)
(  0) 0) |
| [6] |
王彦平, 吕森, 曹琨, 等. 地基SAR多阈值迭代优化PS点选择方法[J]. 信号处理, 2019, 35(6): 1 104-1 110 (Wang Yanping, Lü Sen, Cao Kun, et al. Ground-Based SAR Multi-Threshold Iterative Optimization PS Point Selection Method[J]. Journal of Signal Processing, 2019, 35(6): 1 104-1 110)
(  0) 0) |
| [7] |
李勇发, 左小清, 麻源源, 等. 基于PS-InSAR技术和遗传神经网络算法的矿区地表沉降监测与预计[J]. 地球物理学进展, 2020, 35(3): 845-851 (Li Yongfa, Zuo Xiaoqing, Ma Yuanyuan, et al. Surface Subsidence Monitoring and Prediction Based on PS-InSAR Technology and Genetic Neural Network Algorithm[J]. Progress in Geophysics, 2020, 35(3): 845-851)
(  0) 0) |
| [8] |
Ma P F, Liu Y Z, Wang W X, et al. Optimization of PSInSAR Networks with Application to TomoSAR for Full Detection of Single and Double Persistent Scatterers[J]. Remote Sensing Letters, 2019, 10(8): 717-725 DOI:10.1080/2150704X.2019.1601276
(  0) 0) |
| [9] |
Hay-Man A, Ge L L, Du Z Y, et al. Satellite Radar Interferometry for Monitoring Subsidence Induced by Longwall Mining Activity Using Radarsat-2, Sentinel-1 and ALOS-2 data[J]. International Journal of Applied Earth Observation and Geoinformation, 2017, 61: 92-103 DOI:10.1016/j.jag.2017.05.009
(  0) 0) |
| [10] |
莫莹, 朱煜峰, 江利明, 等. 基于Sentinel-1A的南昌市时间序列InSAR地面沉降监测[J]. 大地测量与地球动力学, 2020, 40(3): 270-275 (Mo Ying, Zhu Yufeng, Jiang Liming, et al. Land Subsidence Monitoring of Nanchang Area Based on Sentinel-1A Using Time Series InSAR Technology[J]. Journal of Geodesy and Geodynamics, 2020, 40(3): 270-275)
(  0) 0) |
2. College of Mining Engineering, North China University of Science and Technology, 80 South-Jianshe Road, Tangshan 063210, China
 2021, Vol. 41
2021, Vol. 41

