2. 中国地震局地球物理勘探中心, 郑州市文化路75号, 450002
震级是地震的基本参数之一,能定量描述地震强弱和大小,常用的震级标准有近震震级ML、面波震级MS、体波震级Mb/MB以及矩震级MW等[1-3]。其中,近震震级是最先被提出的,也是应用较广泛的震级标准,在测震学和地震工程学中有着非常重要的作用[4],其大小是在Wood-Anderson地震仪(以下简写为WA)记录的水平向最大振幅的对数值的基础上,加上相应的地震波随距离衰减校正值而得到的[5-6]。
我国目前使用的测震仪器在记录近场强震信号时会出现限幅,严重影响了地震震级的快速测定,强震仪记录的加速度信号则可以完整记录近场的强地面运动。并且随着强震动观测技术的发展[7],传统的强震动观测技术已拓展应用到地震监测、地震烈度速报、地震预警等领域[8-11],研究一种利用加速度记录来计算近震震级的方法是非常必要的。
1 研究方法有研究表明[12-13],在计算ML震级时,使用仿真WA记录的最大振幅仍然能够得到精确的ML震级值,且使用的WA最大振幅是由速度记录还是由加速度记录仿真而来的对计算结果影响不大[14]。另外,地震波在介质中传播时会发生衰减,其衰减的速率与地下介质的性质关系密切,因此在不同区域计算ML震级时的衰减校正值,即量规函数是有差别的[15-17]。本文利用加速度记录来计算ML震级的方法,必须解决加速度记录仿真WA记录和量规函数的选取这2个问题。
1.1 加速度记录仿真WA记录WA记录是位移记录,有时间域和频率域2种方法。本文采用Kanamori等[18]提出的递归公式,在时间域内将加速度记录实时仿真为WA记录的方法来进行处理。
在仿真WA记录前,利用高通滤波器对加速度数据进行去基线偏移(零漂)处理[18],具体公式为:
| $ {a_j} = \frac{{1 + q}}{2}\frac{{{\xi _j} - {\xi _{j - 1}}}}{g} + q{a_{j - 1}} $ | (1) |
其中,q=0.998,g为加速度计的放大因子,aj和ξj分别为去基线偏移前、后的采样值。
仿真WA记录的递归公式为:
| $ {w_j} = \frac{1}{{{c_2}}}[{g_{{\rm{wa}}}}\Delta {t^2}{a_j} + 2{c_1}{w_{j - 1}} - {w_{j - 2}}] $ | (2) |
式中,c1和c2为常数,由式(3)计算得出;gwa为WA地震计的增益,Δt为采样间隔,aj和wj分别为加速度和WA记录的采样值。
| $ \begin{array}{l} {c_1} = 1 + h{w_0}\Delta t\\ {c_2} = 1 + 2h{w_0}\Delta t + {({w_0}\Delta t)^2} \end{array} $ | (3) |
式中,h为WA地震计的阻尼系数,角频率w0=2πf,f为WA地震计的固有频率,Δt为采样间隔。
1.2 量规函数虽然ML震级的定义为WA记录的水平向最大振幅[6],但在实际计算中往往会使用垂直向的振幅数据。实验结果表明,台基为基岩的台站记录的数据中,水平向和垂直向的最大振幅几乎相同[19-20],而台基为土壤的台站记录的数据中,由于土壤的放大作用,水平向最大振幅值往往比垂直向的大。因此,在台基条件比较复杂的情况下,使用垂直向的振幅数据来计算ML震级比使用水平向振幅数据更为合适[4],并且在使用水平向振幅数据计算ML震级时也要考虑台基的台站校正。原始ML震级的量规函数适用于美国加州地区震源深度较浅的地震,校正距离使用的是震中距,在震源深度较大时一般使用震源距来代替震中距。在新震级国标中,江苏及邻区使用的量规函数为R12,本文采用R12来验证其在江苏地区的适用性。
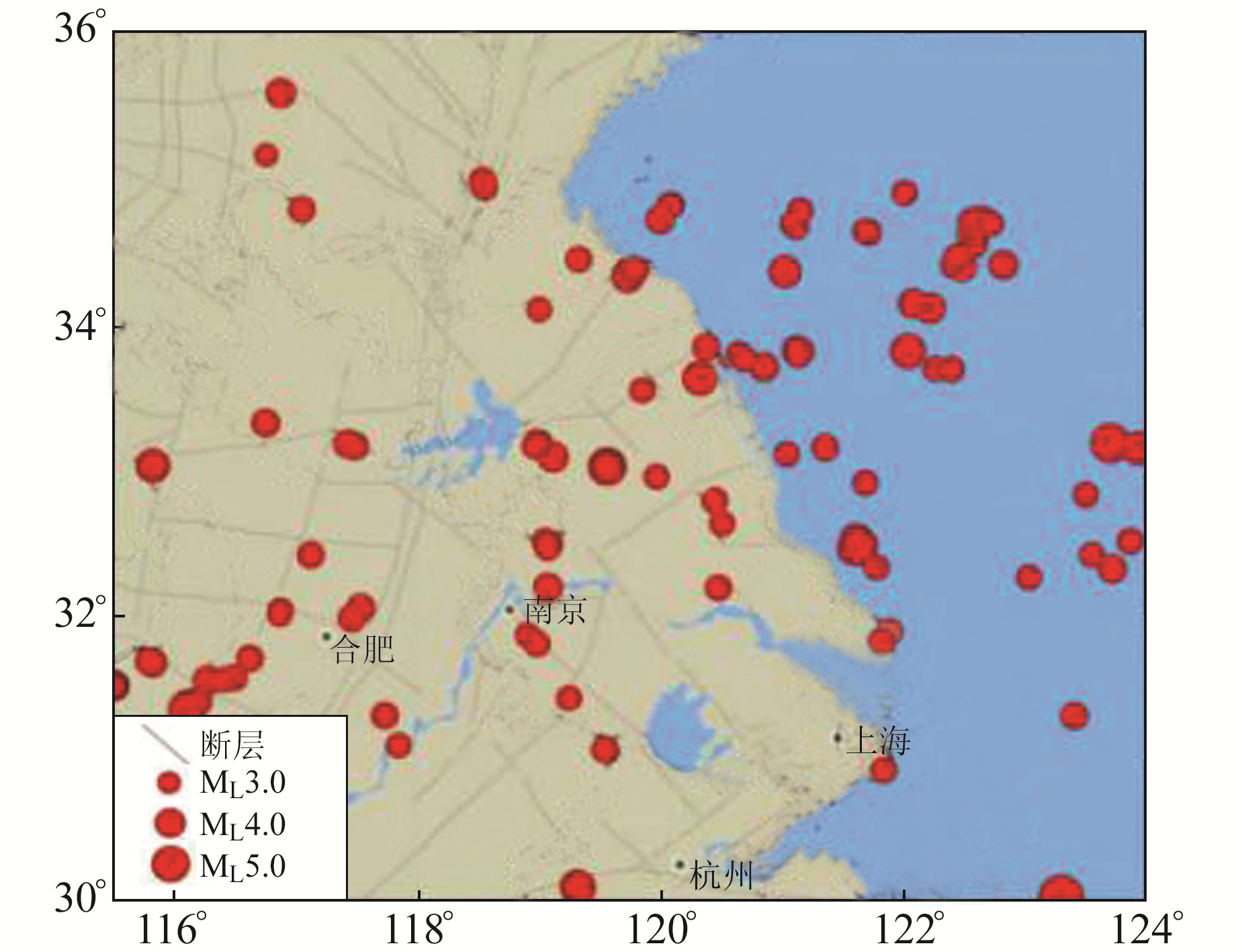
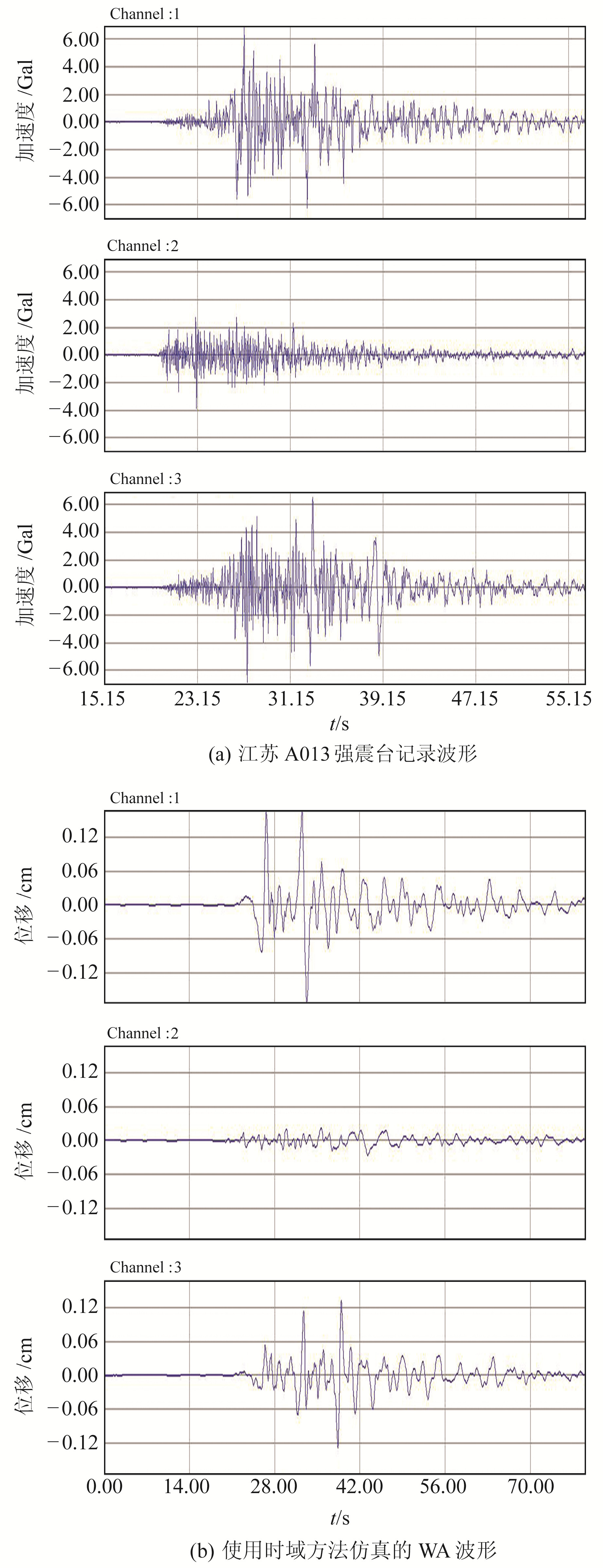
2 在江苏及邻区的应用选用2007~2018年江苏强震台网和江苏测震台网记录到的632次M2.3以上地震进行测试,台站和地震的分布范围在114°~124°E、30°~37°N,其中测震台站72个,强震台站76个。每个地震事件至少有10个台站记录到,选取震中距小于300 km的台站,测量仿真后的S波最大振幅,同一事件根据震中距大小剔除振幅异常的数据,最终得到符合要求的地震事件248次(图 1)。参加计算的振幅值为最大峰值的一半(单位mm),图 2为江苏A013强震台在震中距为36.8 km处加速度记录波形及仿真的WA记录波形。本文采用时间域方法对加速度波形进行仿真,对仿真后的位移波形自动量取水平向最大振幅,取2个水平向的均值,得到15 324个数据,并计算各地震事件的ML震级。
|
图 1 用于基于加速度记录测定震级的地震分布 Fig. 1 Distribution of earthquakes used to determine the magnitude based on acceleration records in this study |
|
图 2 地震波形 Fig. 2 Seismic waveform |
为定量分析基于加速度测定ML震级的可靠性,本文首先采用新震级国标规定的测定方法和量规函数测定了基于加速度记录的震级,并将结果与江苏测震台网基于速度记录测定的震级进行对比分析。江苏数字测震台网进行地震编目时采用“十五”区域测震软件JOPENS-MSDP,地震定位方法采用HYPOSAT方法,走时表采用IASP91表。震级测定时将原始速度波形仿真至WA记录上,量取最大双振幅和相应的周期,并按式(4)计算震级:
| $ \begin{array}{l} {M_L} = {\rm{log}}\frac{{{A_{\mu {\rm{EW}}}} + {A_{\mu {\rm{NS}}}}}}{2} + R\left( \Delta \right) + C\\ {A_\mu } = \frac{{{\rm{count值}}}}{{灵敏度}} \end{array} $ | (4) |
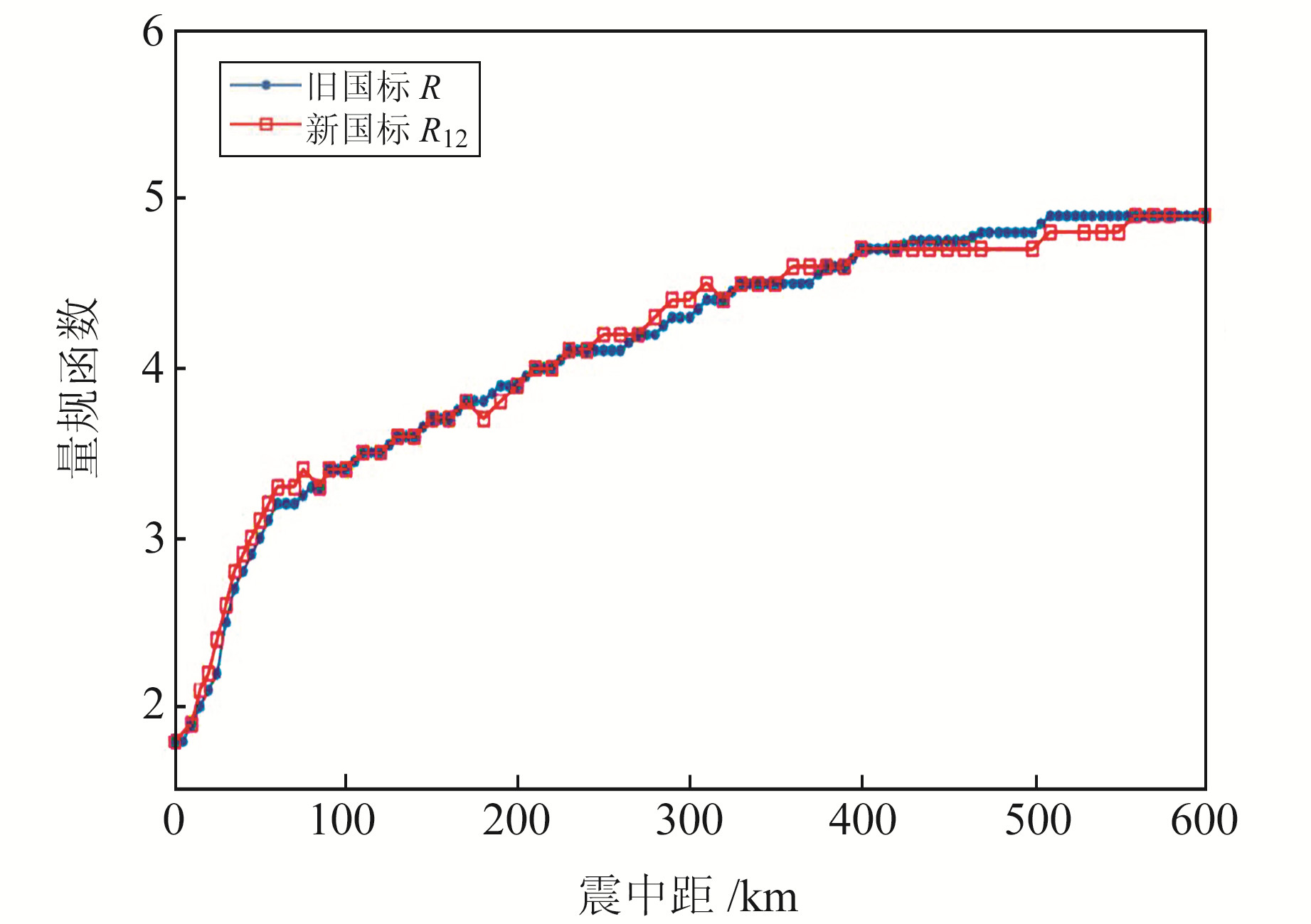
式中,C为台基校正值,由于计算时采用了多台平均方式,所以一般情况下C=0;R(Δ)为起算函数,为旧震级国标中的量规函数,具体见图 3。
|
图 3 新旧量规函数对比 Fig. 3 Comparison of new and old gauge functions |
根据我国新震级国标的有关要求,测定地方性震级应使用仿真成短周期地震仪S波(或Lg波)两个水平向记录的最大振幅,该最大振幅应大于干扰水平2倍以上,计算公式为:
| $ \begin{array}{*{20}{l}} {{M_L} = {\rm{lg}}(A) + R\left( \Delta \right) + C} \end{array} $ | (5) |
式中,
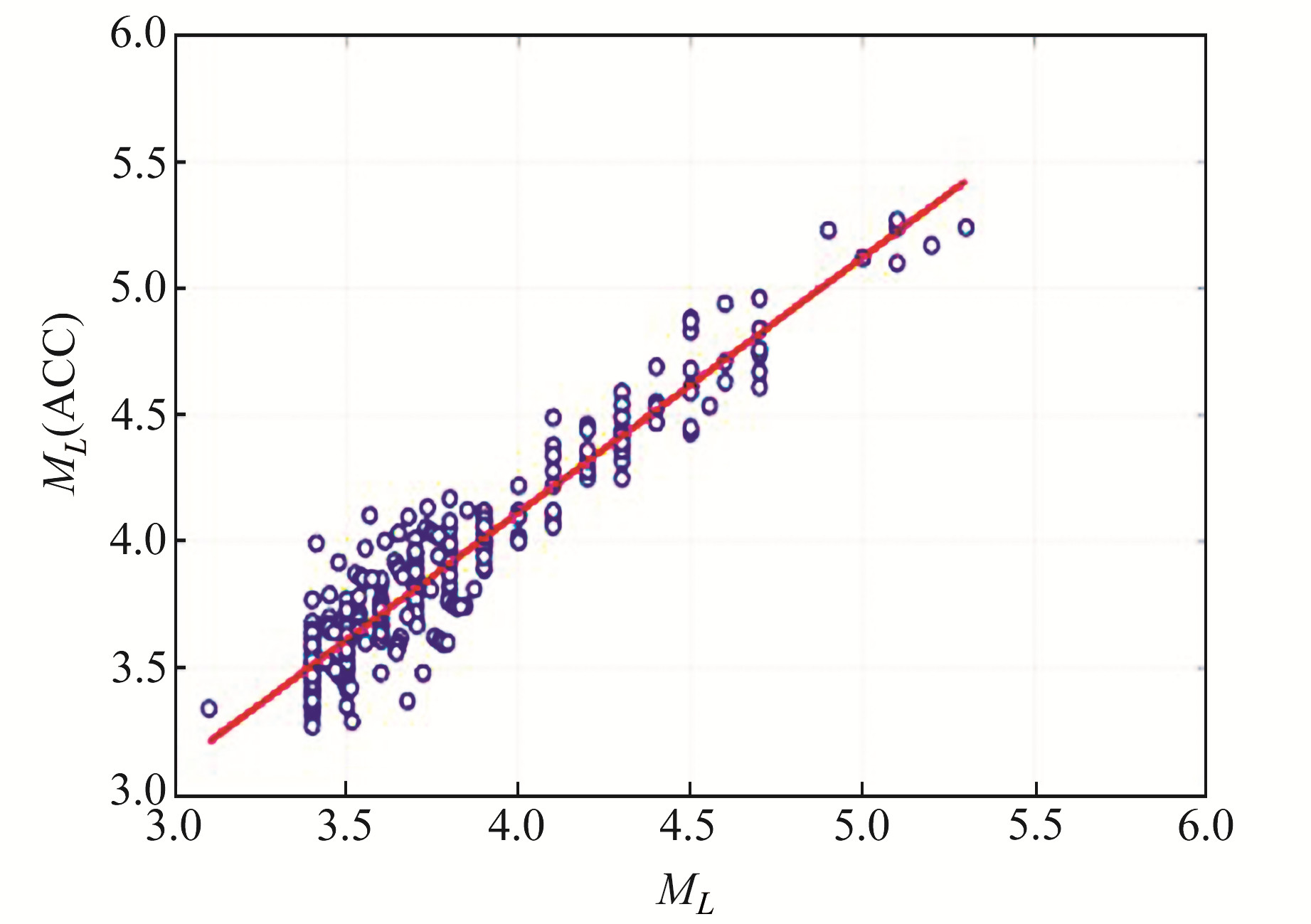
基于加速度记录测定的ML(ACC)震级与ML(速度记录)之间的线性拟合关系(图 4)为:
| $ {M_L}\left( {{\rm{ACC}}} \right) = 0.987{M_L} + 1.371 $ | (6) |
|
图 4 计算得到的ML(ACC)震级与ML震级的关系 Fig. 4 The relationship between ML (ACC) magnitude obtained by calculationand ML magnitude |
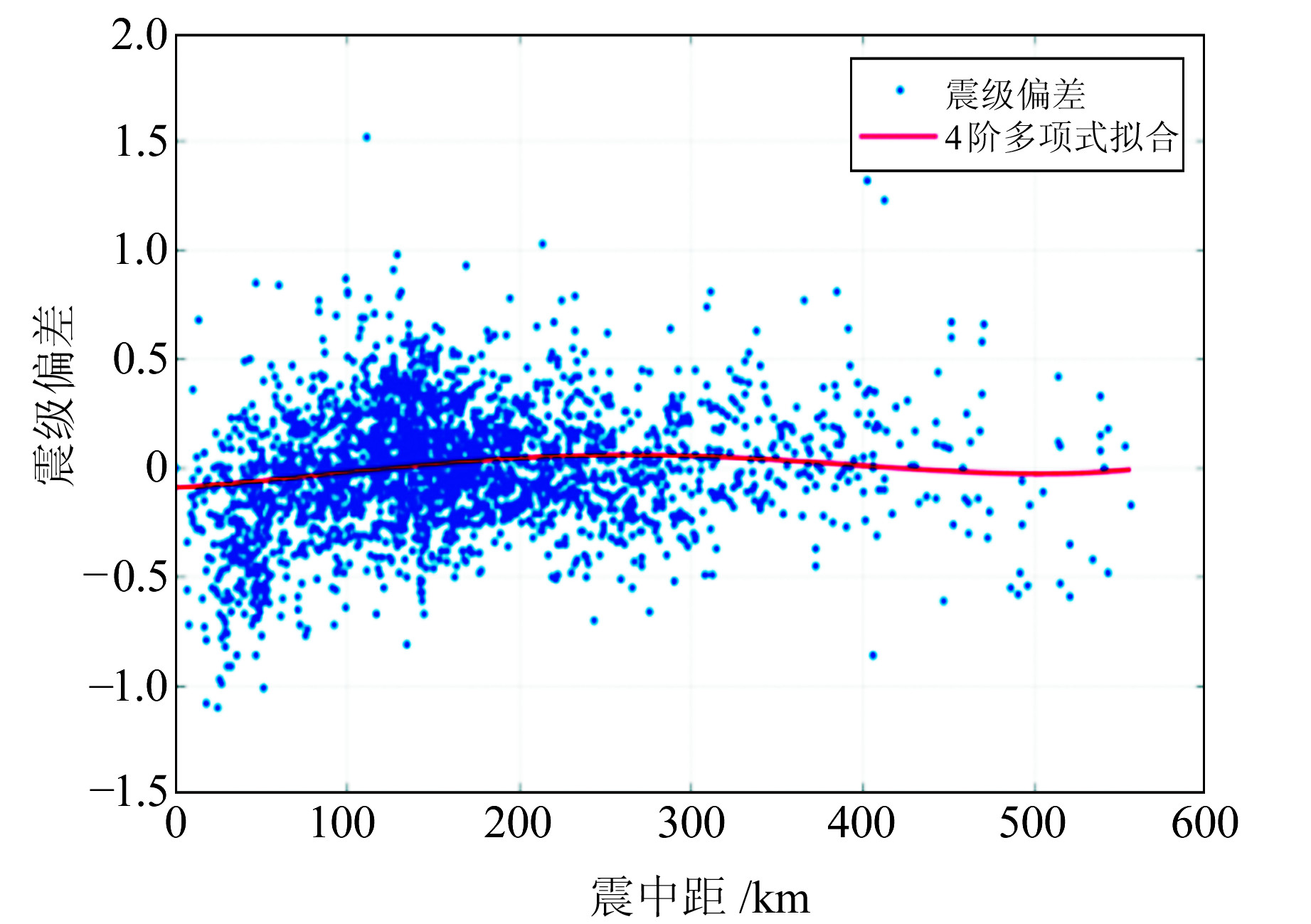
本文还计算了15 324组基于加速度测定的震级与人工编目震级之间的绝对偏差,偏差随震中距变化的分布如图 5所示。统计结果显示,偏差在±0.5级以内的结果占87%;通过4阶多项式拟合后发现,在震中距小于200 km范围内测定的震级略低于人工编目结果,这可能与所用台站数低于人工编目使用的台站数有关,震中距大于200 km范围无系统偏差。总体而言,两者结果的一致性较好。
|
图 5 与人工编目震级之间的误差随震中距的变化特征 Fig. 5 The variation characteristics of the error between magnitude and manual catalogue magnitude with epicentral distance |
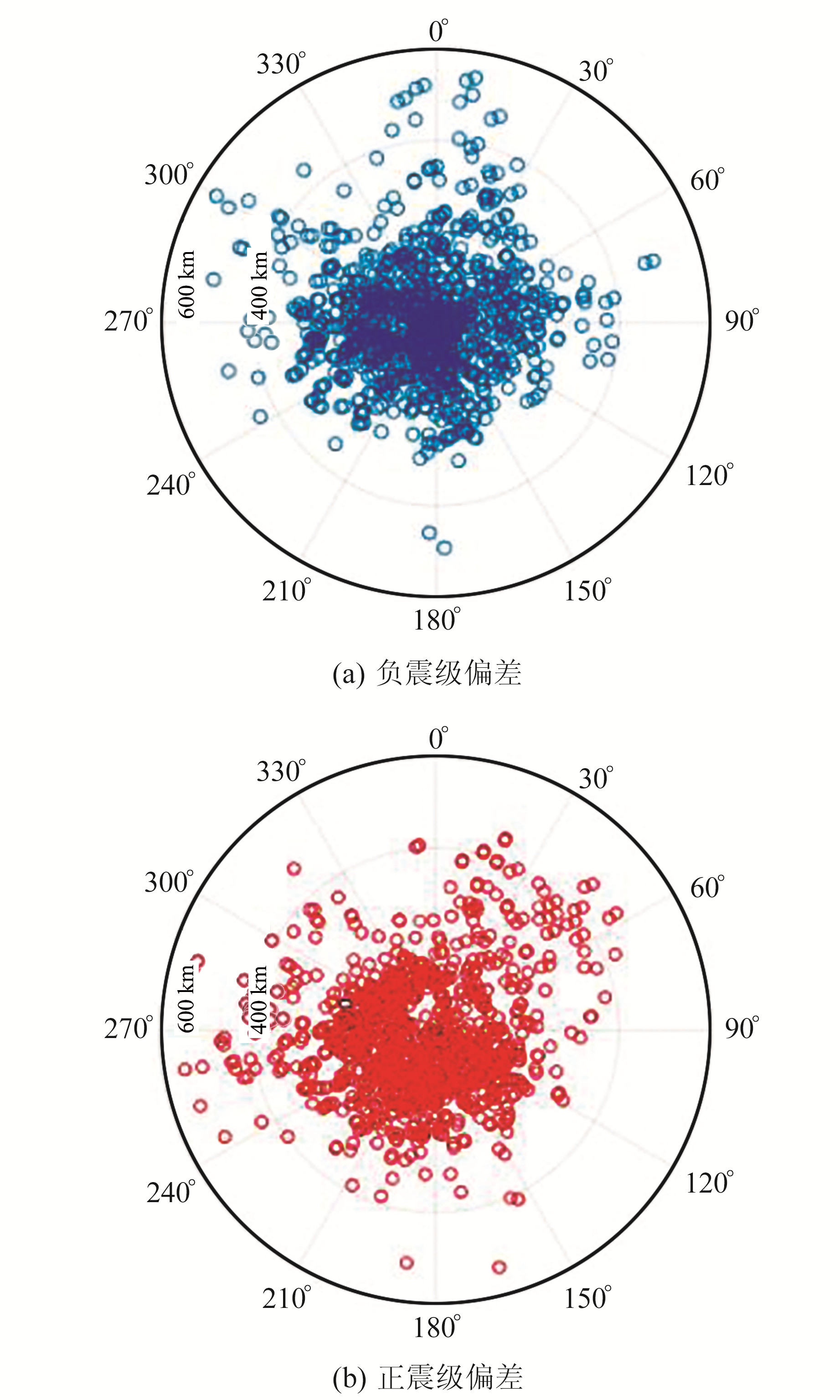
为探究震级偏差在方位上的规律性变化特征,以正N向与地震震中、记录台站连线之间的夹角为方位角,以顺时针方向为正,分析正、负偏差随震中距、反方位角(即360°减方位角)的变化特征。从图 6的结果来看,震级偏差随震中距和反方位角的变化特征总体上不明显,各方位上呈均匀分布状态。
|
图 6 震级偏差随方位的变化 Fig. 6 The variation of magnitude error with azimuth |
在强震发生后,距震中较近的速度型测震仪器往往会由于限幅而无法记录完整的地震波形,影响了地震震级的快速测定,而强震仪记录的加速度信号可以完整地记录近场的强地面运动。本文利用加速度波形记录测定近震震级的方法,在大震速报和地震预警的震级快速测定等方面有重要作用。
本文利用江苏强震台网记录的中强地震波形,初步尝试利用加速度波形记录进行近震震级的测定。为了定量分析基于加速度记录测定近震震级的可靠性,首先采用新震级国标规定的测定方法和量规函数测定了基于加速度记录的震级,并将结果与江苏测震台网基于速度记录测定的震级进行对比分析,得到线性拟合关系式:ML(ACC)=0.987ML+1.371。同时,基于248个地震的15 324组数据,计算其与人工编目震级之间的绝对偏差,结果显示,偏差在±0.5级以内的结果占87%;通过4阶多项式拟合后发现,在震中距小于200 km范围内测定的震级略低于人工编目的结果,震中距大于200 km无系统偏差。两者结果的一致性较好表明,本文利用加速度波形记录仿真WA位移记录来计算ML震级是可行的,计算得到的结果也是可靠的。另外分析了震级偏差在方位上的规律性变化特征,从结果来看,震级偏差随震中距和反方位角的变化特征总体上不明显,各方位上呈均匀分布状态。
在利用历史地震资料的基础上,利用本文计算方法能够计算出较可靠的ML震级值,在大震自动速报时采用实时仿真WA位移记录的方法进行震级的快速测定,对于缩短速报时间、提高速报震级参数的准确性等方面都是非常有意义的。
| [1] |
陈培善, 叶文华. 论中国地震台网测得的面波震级[J]. 地球物理学报, 1987, 30(1): 39-51 (Chen Peishan, Ye Wenhua. On the Surface Wave Magnitude Measured by the Seimic Network in China[J]. Chinese Journal of Geophysics, 1987, 30(1): 39-51)
(  0) 0) |
| [2] |
陈宏峰, 袁菲, 徐志国, 等. 使用中国地震台网资料快速测定中强地震矩震级[J]. 地震地磁观测与研究, 2014, 35(增3): 51-57 (Chen Hongfeng, Yuan Fei, Xu Zhiguo, et al. Rapid Calculation of the Moment Magnitude of Moderate and Strong Earthquakes by Using the Data from China Seismic Network[J]. Seismological and Geomagnetic Observation and Research, 2014, 35(S3): 51-57)
(  0) 0) |
| [3] |
高景春, 赵英萍, 徐志国, 等. 河北省测震台网中小地震矩震级的测定[J]. 华北地震科学, 2011, 29(2): 1-5 (Gao Jingchun, Zhao Yingping, Xu Zhiguo, et al. Study on Moment Magnitude of Small and Moderate Earthquakes Located by Hebei Seismic Network[J]. North China Earthquake Sciences, 2011, 29(2): 1-5)
(  0) 0) |
| [4] |
陈运泰, 吴忠良, 王培德, 等. 数字地震学[M]. 北京: 地震出版社, 2000 (Chen Yuntai, Wu Zhongliang, Wang Peide, et al. Digital Seismology[M]. Beijing: Seismological Press, 2000)
(  0) 0) |
| [5] |
郭履灿, 庞明虎. 面波震级和它的台基校正值[J]. 地震学报, 1981, 3(3): 312-320 (Guo Lücan, Pang Minghu. Surface-Wave Magnitude of Earthquakes and Its Station Correction[J]. Acta Seismologica Sinica, 1981, 3(3): 312-320)
(  0) 0) |
| [6] |
Richter C F. An Instrumental Earthquake Magnitude Scale[J]. Bulletin of the Seismological Society of America, 1935, 25(1): 1-32
(  0) 0) |
| [7] |
康英, 刘杰, 郑斯华, 等. 区域数字台网新参数的求解[J]. 地震地磁观测与研究, 2004, 25(增1): 119-128 (Kang Ying, Liu Jie, Zheng Sihua, et al. Determination of New Parameters in Regional Digital Seismic Network[J]. Seismological and Geomagnetic Observation and Research, 2004, 25(S1): 119-128)
(  0) 0) |
| [8] |
Kanamori H, Jennings P C. Determination of Local Magnitude(ML) from Strong-Motion Accelerograms[J]. Bulletin of the Seismological Society of America, 1978, 68(2): 471-485
(  0) 0) |
| [9] |
Espinosa A F. Attenuation of Strong Horizontal Ground Accelerations in the Western United States and Their Relation to ML[J]. Bulletin of the Seismological Society of America, 1980, 70(2): 583-616
(  0) 0) |
| [10] |
Hatzidimitriou P, Papazachos C, Kiratzi A, et al. Estimation of Attenuation Structure and Local Earthquake Magnitude Based on Acceleration Records in Greece[J]. Tectonophysics, 1993, 217(3-4): 243-253 DOI:10.1016/0040-1951(93)90008-8
(  0) 0) |
| [11] |
章文波, 彭克中. 利用近场地震加速度记录测定近震震级ML的研究[J]. 地震工程与工程振动, 1995, 15(3): 4-11 (Zhang Wenbo, Peng Kezhong. Determination of near Earthquake Magnitude ML Using near-Field Accelerograms[J]. Earthquake Engineering and Engineering Vibration, 1995, 15(3): 4-11)
(  0) 0) |
| [12] |
Uhrhammer R A, Collins E R. Synthesis of Wood-Anderson Seismograms from Broadband Digital Records[J]. Bulletin of the Seismological Society of America, 1990, 80(3): 702-717
(  0) 0) |
| [13] |
Langston C A, Brazier R, Nyblade A A, et al. Local Magnitude Scale and Seismicity Rate for Tanzania, East Africa[J]. Bulletin of the Seismological Society of America, 1998, 88(3): 712-721
(  0) 0) |
| [14] |
Bobbio A, Vassallo M, Festa G. A Local Magnitude Scale for Southern Italy[J]. Bulletin of the Seismological Society of America, 2009, 99(4): 2 461-2 470
(  0) 0) |
| [15] |
Uhrhammer R A, Loper S J, Romanowicz B. Determination of Local Magnitude Using BDSN Broadband Records[J]. Bulletin of the Seismological Society of America, 1996, 86(5): 1 314-1 330
(  0) 0) |
| [16] |
Keir D, Stuart G W, Jackson A, et al. Local Earthquake Magnitude Scale and Seismicity Rate for the Ethiopian Rift[J]. Bulletin of the Seismological Society of America, 2006, 96(6): 2 221-2 230
(  0) 0) |
| [17] |
Askari R, Ghods A, Sobouti F. Calibration of an ML Scale in the Alborz Region, Northern Iran[J]. Bulletin of the Seismological Society of America, 2009, 99(1): 268-276
(  0) 0) |
| [18] |
Kanamori H, Maechling P, Hauksson E. Continuous Monitoring of Ground-Motion Parameters[J]. Bulletin of the Seismological Society of America, 1999, 89(1): 311-316
(  0) 0) |
| [19] |
Alsaker A, Kvame L B, Hansen R A, et al. The ML Scale in Norway[J]. Bulletin of the Seismological Society of America, 1991, 81(2): 379-398
(  0) 0) |
| [20] |
Bindi D, Luzi L, Pacor F, et al. Ground-Motion Predictions from Empirical Attenuation Relationships Versus Recorded Data: The Case of the 1997-1998 Umbria-Marche, Central Italy, Strong-Motion Data Set[J]. Bulletin of the Seismological Society of America, 2006, 96(3): 984-1 002
(  0) 0) |
2. Geophysical Exploration Center of CEA, 75 Wenhua Road, Zhengzhou 450002, China
 2021, Vol. 41
2021, Vol. 41

