2. 应急管理部国家自然灾害防治研究院, 北京市安宁庄路1号, 100085;
3. 中国地震局地震研究所, 武汉市洪山侧路40号, 430071
无线电掩星探测技术具有全天候、全球覆盖、高时空分辨率、低成本的优点,如何反演得到高精度的掩星产品广受关注。对掩星观测数据的获取,如GNSS卫星的精密星历信息是基于地固坐标系(international terrestrial reference system,ITRS)下的坐标[1],而掩星反演计算是在惯性坐标系(Julian epoch 2000.0,J2000)[2-3]下进行的。ITRS坐标转换至J2000坐标过程中需要使用岁差模型和章动模型,2003-01-01后使用比IAU1976和IAU1980模型精度更高的IAU2000A模型[4]。IAU2000A岁差章动模型是一种基于刚性地球的模型,其章动序列包含完整的MHB章动,该模型精度可达0.2 mas[5-7]。LEO(low earth orbit)卫星精密定轨要求定轨精度尽可能高,坐标旋转造成的误差需要考虑;中性大气掩星反演数据处理要求轨道精度优于10 cm,因此在ITRS/J2000转换时要保证坐标转换精度,这对整个掩星反演过程起着尤为重要的作用。
目前,基于IERS官网的坐标转换原理包含4种坐标转换方法,其中基于春分点的经典角坐标转换法精度较高、算法复杂度较低,但通常在ITRS/J2000坐标转换过程中容易忽视海洋潮汐和地球章动引起的极移矩阵高频改正项误差,以及框架间的经度误差、倾角误差和旋转误差等常数偏差矩阵造成的误差。
针对上述问题,同时也为了提高ITRS/J2000坐标转换的精度,本文采用基于春分点的经典角坐标转换法,并采用线性插值、海洋潮汐及章动高频改正项修正,保证ITRS/GCRS坐标转换的精度;再通过常数偏差矩阵的变换,将GCRS坐标转换到J2000平赤道坐标系中。同时,分析季节及Kp、Dst、F107等指数[8]对坐标转换以及中性大气掩星反演的影响。最后,针对ITRS/J2000坐标转换提出建议和措施,以减小坐标转换造成的精度损失。
1 算法原理和步骤本文选择基于春分点的经典角坐标转换法,ITRS与J2000坐标系的差别体现在极移、地球自转和岁差章动上。ITRS/J2000坐标转换如下[9]:
| $ {\mathit{\boldsymbol{r}}_{{\rm{J2000}}}} = {\mathit{\boldsymbol{B}}^{\rm{T}}}({\mathit{\boldsymbol{M}}_{Q(t)}}{\mathit{\boldsymbol{M}}_{R(t)}}{\mathit{\boldsymbol{M}}_{W(t)}}){\mathit{\boldsymbol{r}}_{{\rm{ITRS}}}} $ | (1) |
式中,rJ2000为转换后的J2000惯性系下的坐标向量,B为常数偏差矩阵,MQ(t)为岁差章动矩阵,MR(t)为地球自转矩阵,MW(t)为极移矩阵,rITRS为待转换的地固系下的坐标向量。
岁差章动矩阵MQ(t)根据所选的转换模式而有所区别,本文基于春分点的经典角模式下MQ(t)计算公式如下:
| $ {\mathit{\boldsymbol{M}}_{Q(t)}} = \mathit{\boldsymbol{B}} \cdot \mathit{\boldsymbol{P}}(t) \cdot \mathit{\boldsymbol{N}}(t) $ | (2) |
式中,B为常数偏差矩阵,P(t)为岁差矩阵,N(t)为章动矩阵,岁差矩阵和章动矩阵随时间变化。B矩阵的计算公式如下:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{R}}_z}({J_{{\rm{ra}}}}){\rm{ }}\cdot{\mathit{\boldsymbol{R}}_y}({\delta _{{\rm{lon}}}}){\rm{ }}\cdot{\mathit{\boldsymbol{R}}_x}({\delta _{{\rm{obl}}}})} \end{array} $ | (3) |
| $ {\mathit{\boldsymbol{R}}_x}(\alpha ) = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{{\rm{cos}}\alpha }&{{\rm{sin}}\alpha }\\ 0&{ - {\rm{sin}}\alpha }&{{\rm{cos}}\alpha } \end{array}} \right] $ | (4) |
| $ {\mathit{\boldsymbol{R}}_y}(\alpha ) = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\alpha }&0&{ - {\rm{sin}}\alpha }\\ 0&1&0\\ {{\rm{sin}}\alpha }&0&{{\rm{cos}}\alpha } \end{array}} \right] $ | (5) |
| $ {\mathit{\boldsymbol{R}}_z}(\alpha ) = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\alpha }&{{\rm{sin}}\alpha }&0\\ {{\rm{ - sin}}\alpha }&{{\rm{cos}}\alpha }&0\\ 0&0&1 \end{array}} \right] $ | (6) |
式中,δobl为J2000坐标系倾角校正参数,大小为3.306 041 454 222 148×10-8 rad;δlon为J2000坐标系经度校正参数,大小为-8.056 217 146 976 144×10-8 rad;Jra为J2000平均春分点的旋转角,大小为-7.078 279 744 199 226×10-8 rad。Rx、Ry、Rz为3个轴方向的旋转函数。
MQ(t)矩阵为地球自转矩阵,根据所选模式不同计算方法也不同,本文采用格林威治时间计算。
MW(t)为极移矩阵,主要通过IERS观测数据、模型计算出的海洋潮汐和章动误差高频改正项组成。计算公式如下:
| $ {\mathit{\boldsymbol{M}}_{W(t)}} = {\mathit{\boldsymbol{R}}_n}( - s'){\rm{ }}\cdot{\mathit{\boldsymbol{R}}_m}({x_p}){\rm{ }}\cdot{\mathit{\boldsymbol{R}}_l}({y_p}) $ | (7) |
式中,参数-s′可由xp和yp计算得到,(xp, yp)计算公式如下:
| $ ({x_p}, {y_p}) = (x″, y″) + {(\delta x, \delta y)_{{\rm{tides}}}} + {(\delta x, \delta y)_{{\rm{nutation}}}} $ | (8) |
式中,(x″, y″)由IERS观测文件EOP参数线性插值得到,(δx, δy)tides和(δx, δy)nutation通过模型计算得到。
2 实验对比分析ITRS/J2000坐标转换过程中涉及到3个转换矩阵,同时需要对高频改正项和常数偏差矩阵加以考虑,为了分析极移矩阵MW(t)中高频改正项和岁差章动矩阵MQ(t)中常数偏差矩阵对坐标转换精度影响的大小,下面从极移的高频改正项误差、常数偏差矩阵误差及坐标转换误差对掩星反演的影响3个部分进行阐述,均使用长期C04形式的EOP地球参数进行转换。
2.1 极移的高频改正项误差地球极移矩阵中高频改正项包括海洋潮汐引起的误差和章动引起的误差。Yoder等[10]首先提出由于极距惯性的潮汐变形引起UT1的周期性变化,包括地球解耦岩心的纬向潮汐变形、地表弹性和海洋平衡。Chao等[11]论述1 d和0.5 d章动源自外部太阳单轴等扭矩对地球非轴对称部分的直接影响,指定为极运动的章动效应。海洋潮汐、地球章动等影响直接体现在坐标转换精度上,下面对其造成的影响进行数据分析。
对加高频改正项前后的坐标转换误差进行分析,将其转换结果作差按月求平均,结果如图 1所示。由图可知,高频改正项误差呈现纺锤形变化,与海洋潮汐和章动高频改正项随时间变化有关。对误差的均值和标准差进行统计分析表明,该项误差对坐标转换造成均值0.06 mm、标准差0.44 m的影响。三轴误差呈现近似周期性变化,符合高频改正项中潮汐变化引起的误差变化规律。

|
图 1 不同季节潮汐章动对坐标转换的影响 Fig. 1 Influence of precession nutation during different season on coordinate conversion |
ITRS/J2000的转换精度还与季节有关,随着四季更替,地球周围磁场发生变化,图 2统计了2019年每个季节的坐标转换误差偏差的均值和标准差。夏季、秋季和冬季误差在纵坐标轴0±0.07 mm范围内波动,误差较小;春季误差约为0.23 mm,是其他季节的3倍,说明春节坐标转换时潮汐章动高频改正项造成的误差较大,建议使用快速更新和预报的EOP参数进行坐标转换。
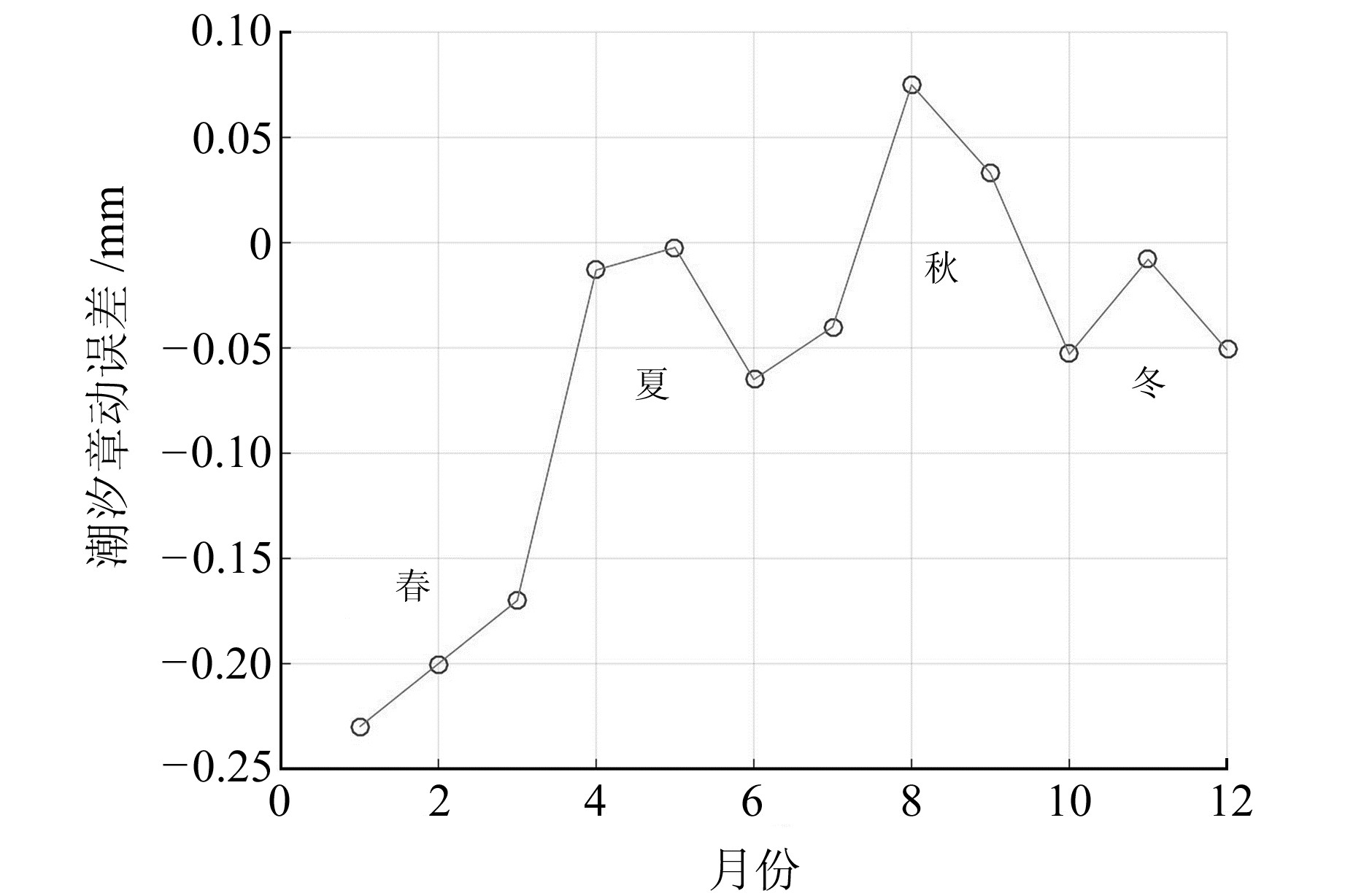
|
图 2 潮汐章动误差季节性分析 Fig. 2 Seasonal analysis of precession nutation error |
为了研究海洋潮汐和章动高频改正项对坐标转换的影响与地磁活动、太阳活动的关系,下面对2019年的Kp、Dst、F107指数进行对比分析,如图 3所示,其中图 3(a)表示Kp、Dst、F107随时间变化曲线,图 3(b)表示相应时间内潮汐章动引起的坐标转换误差变化曲线。由图 3(a)和图 3(b)对比可知,Dst指数和F107指数全年比较平静,高频改正项造成的坐标转换误差分别在2019年第52天、第220天、第300天差别较大,与其相应时间段内的Kp指数也增长到了30以上,该现象可能是由于地磁活动造成对坐标转换的影响,建议Kp指数较大时采用快速更新和预报的EOP参数进行坐标转换,以减小坐标转换的精度损失。
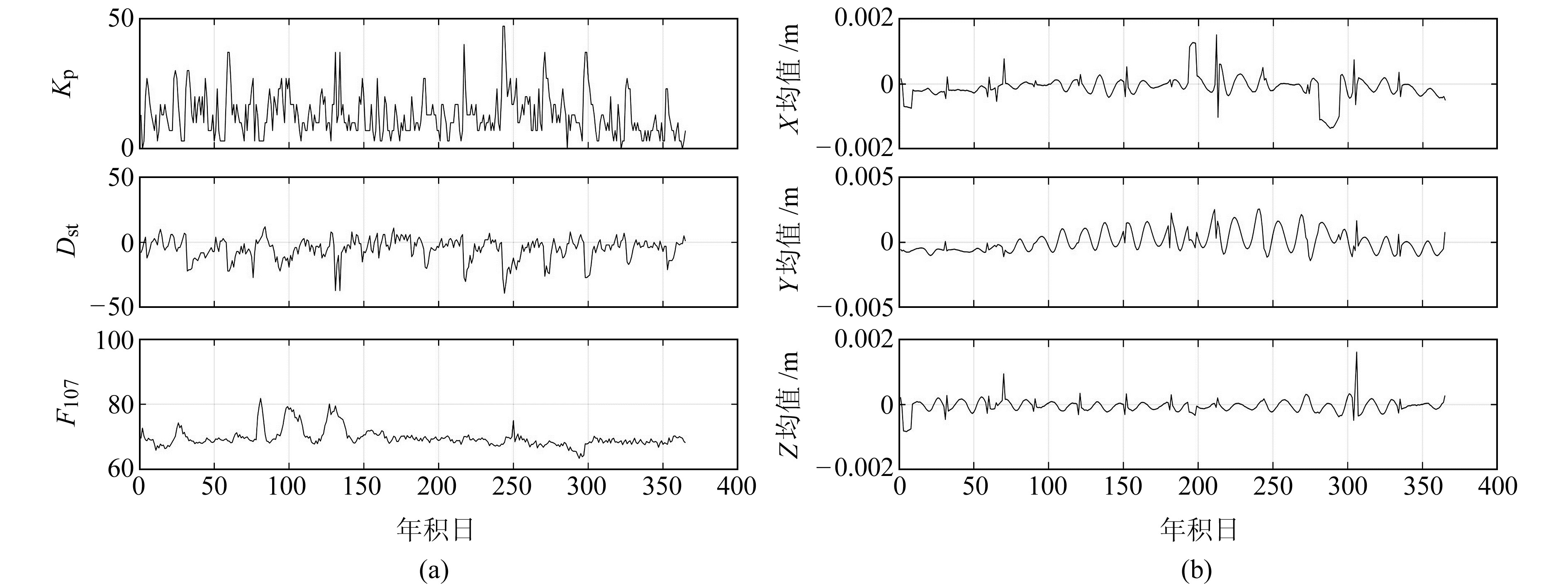
|
图 3 地磁指数与太阳活动指数对坐标转换精度的影响 Fig. 3 Influence of geomagnetic index and solar activity index on coordinate conversion precision |
常数偏差矩阵B表征了GCRS框架与J2000框架间偏差的大小。GCRS与J2000框架间在经度方向上存在偏差,坐标轴倾角也存在偏差,以及坐标轴间存在一定的旋转角度。上述3种偏差均可近似看作常数,分别通过相应的3×3矩阵表达,通过对GCRS框架下的坐标乘以相应的改正矩阵即可转换到J2000坐标系下。图 4统计了2019年全年的常数偏差矩阵B对IGS精密星历坐标转换的影响。

|
图 4 不同季节常数偏差矩阵对坐标转换的影响 Fig. 4 Influence of constant deviation matrix of different season on coordinate transformation |
对加常数偏差矩阵B改正项前后的坐标转换误差进行分析,将其转换结果作差按月求均值,如图 4所示。由图可知,误差呈随机噪声误差形式分布;从均值和标准差进行分析,常数偏差矩阵对坐标转换造成均值-0.028 m、标准差1.7 m的影响。
2.3 坐标转换误差对掩星反演的影响为了分析潮汐章动误差和常数偏差矩阵引起的坐标转换误差对中性大气掩星反演的影响,加入潮汐章动改正项并将常数偏差矩阵旋转后分析反演出的大气干温产品偏差。中性大气掩星反演主要根据低轨卫星LEO观测数据、GPS/BDS掩星精密轨道和LEO精密轨道信息计算得到大气附加相位延迟,通过大气附加相位延迟求出附加多普勒频移以及L1频点的弯曲角,估计出掩星平面的方位角信息,对曲率中心进行修正,组合弯曲角消去电离层影响,用气象模型优化弯曲角,然后进行ABEL积分变换计算出大气折射率廓线,最后由Smith-Weintraub方程、理想气体方程、流体静力学方程计算出干温产品[12]。潮汐章动和常数偏差矩阵会影响GPS/BDS掩星和LEO卫星的轨道精度,我们通过带有误差的轨道反演得到的中性大气干温产品的差异分析误差的影响,将该带误差的轨道引入张衡一号电磁星掩星反演过程中。由图 5、图 6可知,潮汐章动误差引起0.09 K的温度偏差,常数偏差矩阵引起0.19 K的温度偏差,因此中性大气掩星反演必须对潮汐章动误差和常数偏差矩阵进行修正。
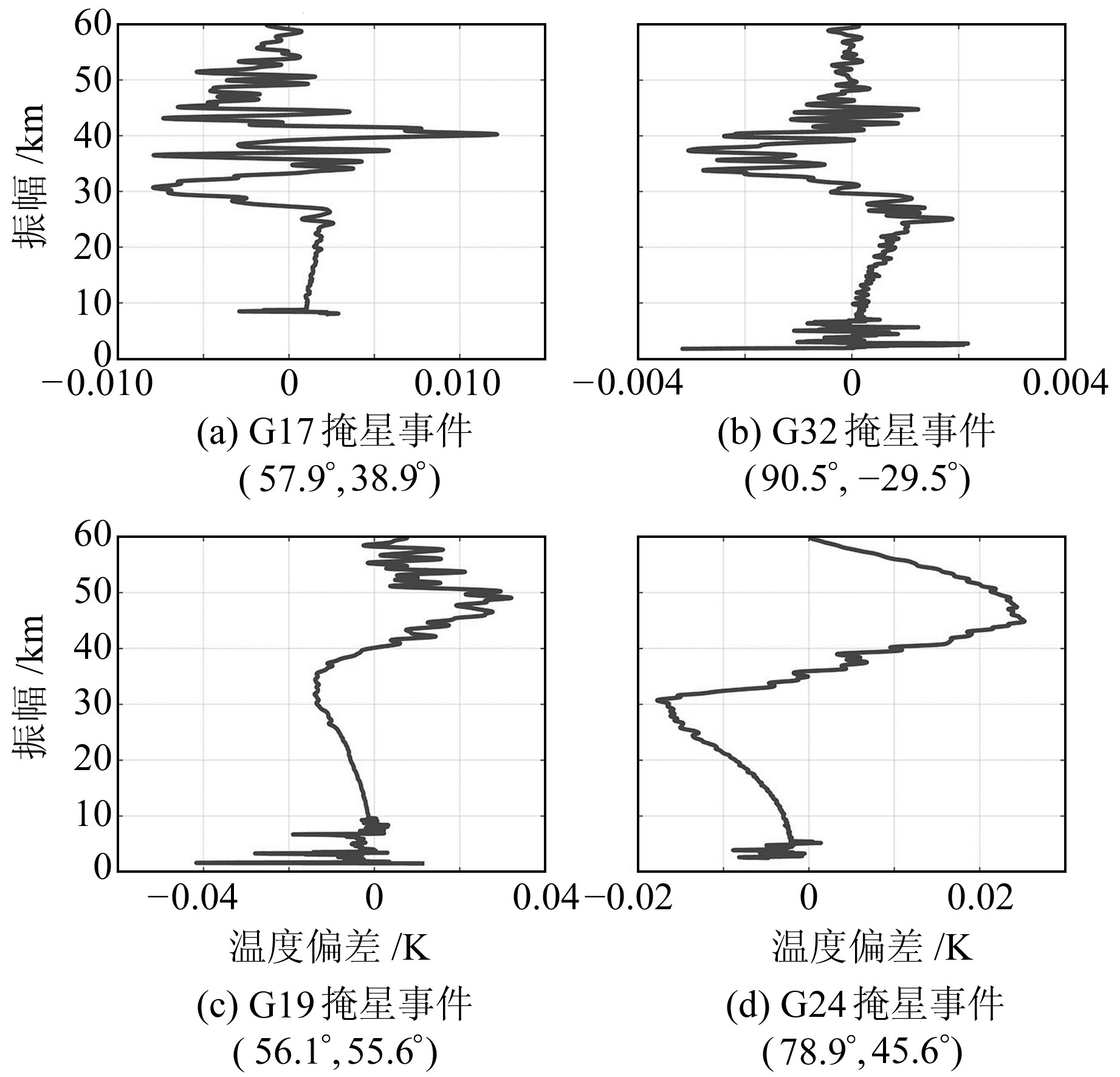
|
图 5 潮汐章动误差引起的反演温度偏差 Fig. 5 Inversion temperature deviation caused by tidal nutation error |
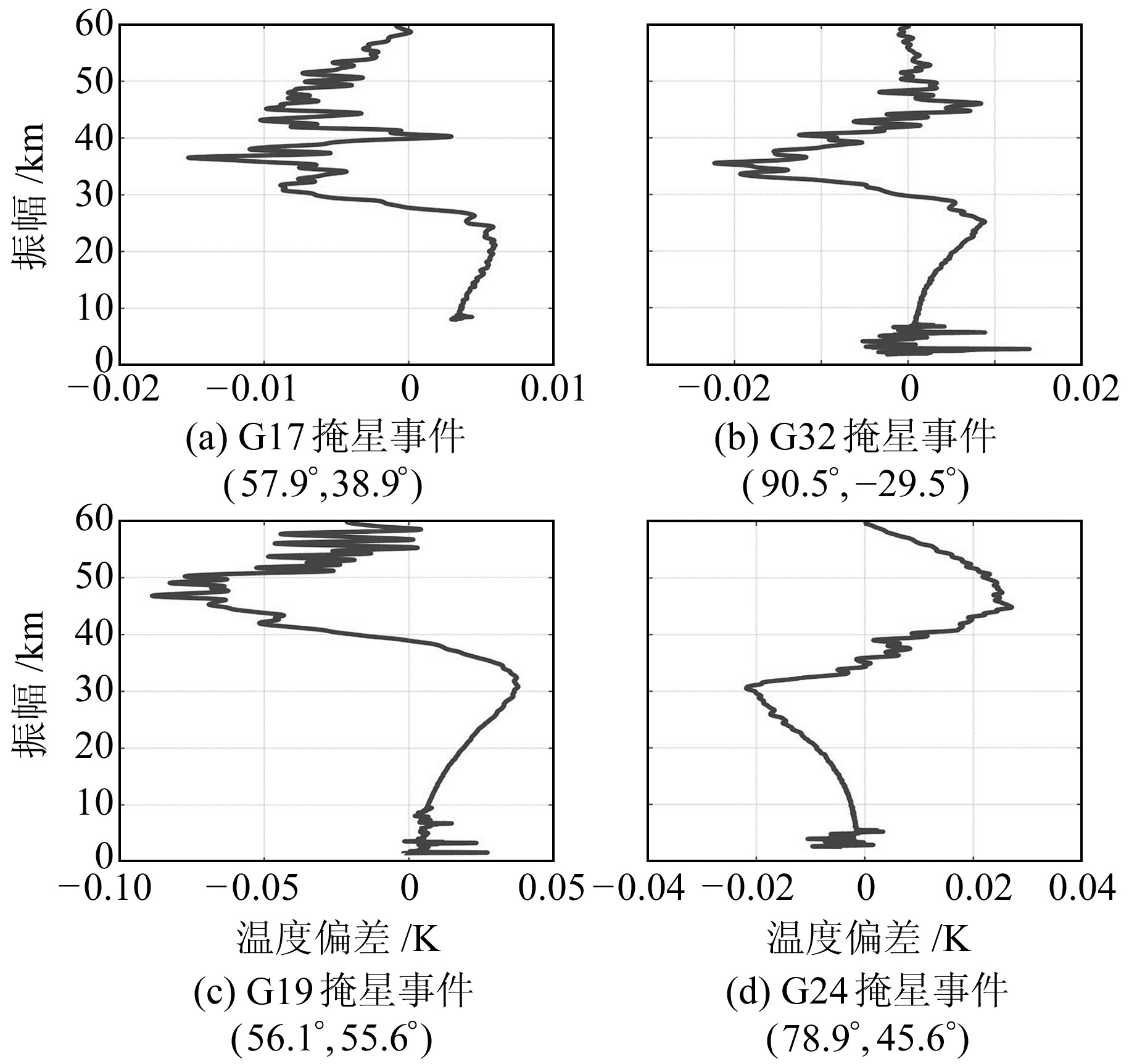
|
图 6 常数偏差矩阵引起的反演温度偏差 Fig. 6 Inversion temperature deviation caused by constant deviation matrix |
本文对2019年的IGS精密星历数据坐标(ITRS)进行不同误差选项下的转换分析,其中高频改正项误差随季节的变化从分析结果来看符合规律;对ITRS转换至J2000过程中的潮汐章动误差和常数偏差矩阵B造成的精度影响进行分析,并研究坐标转换误差与地磁指数和太阳活动指数的关系。得出结论如下:
1) 高频改正项可以造成0.44 m误差(偏差的标准差),严重影响精密定轨精度和掩星数据数据处理精度,在进行ITRS转换至J2000时必须加以改正。
2) IERS极移和时间UT1观测数据均为UTC 0 h,由于待转换时刻与0 h时间间隔的不同可造成0~0.2 m误差,需线性插值到所需时刻。
3) 海洋潮汐和章动高频改正项误差随季节变化而变化,在春季造成的转换误差是夏季、秋季和冬季的3倍,建议在春季使用快速更新和预报的Bulletin A,而不是C04地球参数。
4) 海洋潮汐和章动高频改正项误差随地磁指数Dst和太阳活动指数F107变化不明显,随磁指数Kp变化而变化,建议在Kp指数大于30时采用快速更新和预报的Bulletin A参数,而不是C04地球参数。
5) 在Kp指数出现较大值时高频改正项造成的坐标转换误差不一定变大,规律性不明显,后期需要增加实验分析数据量验证该现象。
6) 通常转换出的是GCRS惯性坐标,需要经过常数偏差矩阵进行变换得到J2000平赤道坐标,B常数矩阵可以造成1.7 m误差,在精密定轨和掩星数据处理时必须加以改正。
7) 在进行中性大气掩星反演过程中,潮汐章动误差可对温度反演造成0.09 K偏差,常数偏差矩阵可对温度反演造成0.19 K偏差,必须加以改正。
| [1] |
李征航, 魏二虎, 王正涛, 等. 空间大地测量学[M]. 武汉: 武汉大学出版社, 2010 (Li Zhenghang, Wei Erhu, Wang Zhengtao, et al. Space Geodesy[M]. Wuhan: Wuhan University Press, 2010)
(  0) 0) |
| [2] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2010)
(  0) 0) |
| [3] |
徐贤胜. GPS/LEO无线电掩星全息反演技术[D]. 上海: 上海大学, 2012 (Xu Xiansheng. GPS/LEO Radio Occultation Holographic Inversion Technology[D]. Shanghai: Shanghai University, 2012)
(  0) 0) |
| [4] |
Capitaine N, Mathews P M, Dehant V, et al. On the IAU 2000/2006 Precession-Nutation and Comparison with other Models and VLBI Observations[J]. Celestial Mechanics and Dynamical Astronomy, 2009, 103(2): 179-190 DOI:10.1007/s10569-008-9179-9
(  0) 0) |
| [5] |
Wallace P T, Capitaine N. Precession-Nutation Procedures Consistent with IAU 2006 Resolutions[J]. Astronomy and Astrophysics, 2006, 459(3): 981-985 DOI:10.1051/0004-6361:20065897
(  0) 0) |
| [6] |
McCarthyD D, Petit G. IERS Conventions, IERS Technical Note 32[Z]. IERS Convention Center, Sevres, France, 2004
(  0) 0) |
| [7] |
Petitt G, Luzum B. IERS Conventions(2010), IERS Technical Note 36[Z]. Frankfurt am Main: Verlag des Bundesamts fur Kartographie and Geodesy, 2010
(  0) 0) |
| [8] |
徐晓华, 罗佳. COSMIC掩星折射指数廓线的统计验证[J]. 武汉大学学报: 信息科学版, 2009, 34(2): 214-217 (Xu Xiaohua, Luo Jia. Statistical Validation of COSMIC Radio Occultation Refractivity Profiles[J]. Geomatics and Information Science of Wuhan University, 2009, 34(2): 214-217)
(  0) 0) |
| [9] |
张捍卫, 郑勇, 马高峰. GCRS与ITRS之间的坐标转换研究[J]. 大地测量与地球动力学, 2011, 31(1): 63-67 (Zhang Hanwei, Zheng Yong, Ma Gaofeng. On Coordinate Transformation between GCRS and ITRS[J]. Journal of Geodesy and Geodynamics, 2011, 31(1): 63-67)
(  0) 0) |
| [10] |
Yoder C F, Williams J G, Parke M E. Tidal Variations of Earth Rotation[J]. Journal of Geophysical Research: Solid Earth, 1981, 86(B2): 881-891 DOI:10.1029/JB086iB02p00881
(  0) 0) |
| [11] |
Chao B F, Dong D N, Liu H S, et al. Libration in the Earth's Rotation[J]. Geophysical Research Letters, 1991, 18(11): 2 007-2 010 DOI:10.1029/91GL02491
(  0) 0) |
| [12] |
苟小平, 符养, 郭粤宁, 等. COSMIC计划及掩星数据误差分析[J]. 气象科学, 2009, 29(3): 348-350 (Gou Xiaoping, Fu Yang, Guo Yuening, et al. COSMIC Mission and Error Analysis of GPS Radio Occultation Data[J]. Scientia Meteorologica Sinica, 2009, 29(3): 348-350)
(  0) 0) |
2. National Institute of Natural Hazards, MEM, 1 Anningzhuang Road, Beijing 100085, China;
3. Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China
 2021, Vol. 41
2021, Vol. 41


