2. 中国测绘科学研究院, 北京市莲花池西路28号, 100830;
3. 辽宁工程技术大学测绘与地理科学学院, 辽宁省阜新市龙湾南大街188号, 123000
精密单点定位技术(precise point positioning,PPP)相比于网络RTK等高精度定位服务系统具有独特优势:总成本和运营服务等方面投资较低;无需像差分定位模式一样,需要借助地面参考站才能获取高精度的定位结果;作用范围广,不受限于基准站间距离,可以直接获取cm级定位精度[1]。PPP技术广泛应用于测绘、地质勘测等,但该技术以差分方式消除电离层延迟误差,载波相位的整周模糊度无法快速固定,进而导致其定位收敛速度较慢[2]。
国内外许多学者对如何加快PPP定位收敛速度进行了广泛而深入的研究。宋超等[3]根据短时间内对流层延迟误差变化较为平稳的特点,利用预先估计的对流层延迟参数作为先验信息,进行附加对流层信息约束的PPP定位,结果表明,PPP重新收敛的速度明显加快,且约束越强收敛速度越快;Li等[4]采用非差非组合的方式,将电离层延迟误差作为未知数进行参数估计,利用IGS电离层工作组(IGS ionosphere working group,Iono-WG)提供的全球电离层格网图(global ionosphere maps,GIM)作为附加电离层约束条件,结果表明,此种方法对于收敛速度的加快和定位精度的提高均有促进作用;Yan等[5]分别利用附近地面参考站解算和IGS所提供的两种不同来源的电离层延迟信息STEC和VTEC,进行附加电离层约束的PPP定位实验,结果表明,附近参考站所提供的电离层延迟信息可显著缩短PPP定位收敛时间,而GIM产品对PPP定位结果的影响取决于GIM产品的数据质量。
基于上述研究,附加电离层约束PPP的定位结果与先验电离层信息的质量有关。本文采用美国西海岸CORS网内的参考站观测数据,进行区域电离层建模,获取高精度电离层先验信息,作为附加约束条件进行PPP定位,并且详细阐述了区域电离层建模方法、附加电离层约束数学模型的公式推导过程;通过大量实验数据,对比分析无电离层组合模型、非差非组合模型和附加电离层约束的非差非组合模型3种算法的PPP定位表现,验证该算法的有效性。
1 电离层延迟建模电离层延迟误差在PPP定位以及其他GNSS定位技术中,都属于最大的误差源之一,对于定位结果的影响程度较大,目前较好的处理方法是采用无电离层组合模型,可以消除电离层误差一阶项的影响,但是只可针对双频用户使用,且无电离层组合估计方法处理能力有限。所以,在PPP定位过程中,能够合理有效地对电离层延迟误差进行最优处理,将影响着整个PPP定位算法的精度和可靠性[6]。
由于电离层对电磁波的折射作用,不同频率电磁波的传播速度不同[7]。根据该特点,本文采用载波相位观测值平滑伪距观测值方法,计算得到高精度的TEC值[8]。
| $ \begin{array}{c} {\rm{STEC}} = \frac{{f_1^2f_2^2}}{{40.28(f_1^2 - f_2^2)}}\left\{ {\left[ {({L_1} - {L_2}) + } \right.} \right.\\ \frac{1}{N}\sum\limits_{n = 1}^N {({P_2} - {P_1}) - ({L_1} - {L_2})]} + \\ c({\rm{DC}}{{\rm{B}}_{\rm{r}}} + {\rm{ DC}}{{\rm{B}}^{\rm{s}}}){\rm{ }}\} \end{array} $ | (1) |
式中,f为载波相位的频率,N为历元数,P1和P2为伪距观测值,L1和L2为载波相位观测值,DCBr为接收机的差分码偏差,DCBs为卫星的差分码偏差。
由于地面接收机与空中不同卫星之间的传播路径各不相同,故各个方向上的TEC值也不同。这些TEC值之中,天顶方向总电子量VTEC值是最小的[9],一般通过投影函数对传播路径方向的总电子含量STEC和天顶方向的总电子含量VTEC进行投影转换。投影函数为:
| $ mf(z) = \frac{1}{{{\rm{cos}}z'}}, {\rm{sin}}z' = \frac{R}{{R + H}}{\rm{sin}}\alpha z $ | (2) |
式中,mf为投影函数,z为测站的天顶距,R和H分别为地球半径和假定电离层薄层厚度。
将上述方法所获得的VTEC值通过模型拟合可得到电离层模型,表示天顶总电子含量的球谐函数模型为[10]:
| $ \begin{array}{c} VTEC(\varphi , \lambda ) = \\ \sum\limits_{n = 0}^{{n_{{\rm{max}}}}} {\sum\limits_{m = 0}^n {\tilde p} } {\rm{sin}}\varphi ({a_{nm}}{\rm{cos}}m\lambda + {b_{nm}}{\rm{sin}}m\lambda ) \end{array} $ | (3) |
式中,VTEC为天顶方向总电子含量,φ和λ分别为地磁纬度和日固经度,n和m分别为球谐函数的阶数,
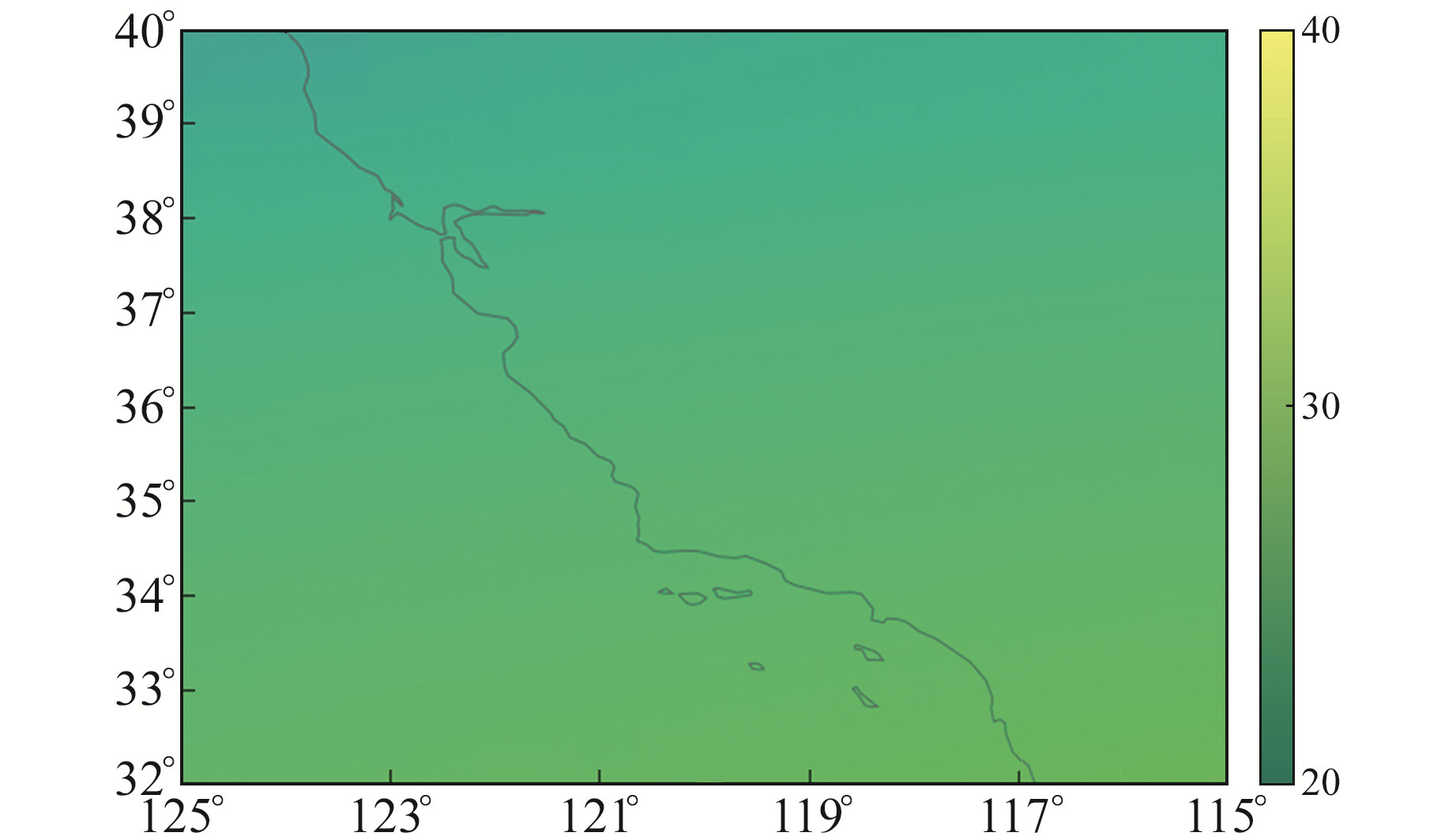
本文实验数据采用美国西海岸CORS网参考站所采集的观测数据,实验区域范围为32°~40°N、115°~125°W,观测时间为2020-01-01~2020-01-03,采样间隔为1 s,卫星截止高度角为10°,各参考站站点的精确坐标可由SOPAC网站获得,站点位置分布均匀,观测数据连续。对183个地面参考站的观测数据进行数据处理,进而建立区域电离层延迟模型,图 1显示了UTC 2020-01-01 07:00的电离层总电子含量结果。
|
图 1 UTC 2020-01-01 07:00的电离层总电子含量 Fig. 1 Total electron content in the ionosphere at 07:00 UTC on January 1, 2020 |
实验对比了无电离层组合模型、非差非组合模型和附加电离层约束的非差非组合模型3种不同情况下的PPP定位结果,以评估附加电离层约束算法对于提高PPP定位精度和加快收敛速度的适用性。
为了验证附加电离层约束算法对于PPP定位的有效性,选用美国西海岸CORS网内8个参考站(TRLK、ALTH、P300、CRCN、MULN、DONO、CHOW、P512)2020年年积日001全天24 h的观测数据进行测试,对比上述3种不同PPP定位模型的相关表现。
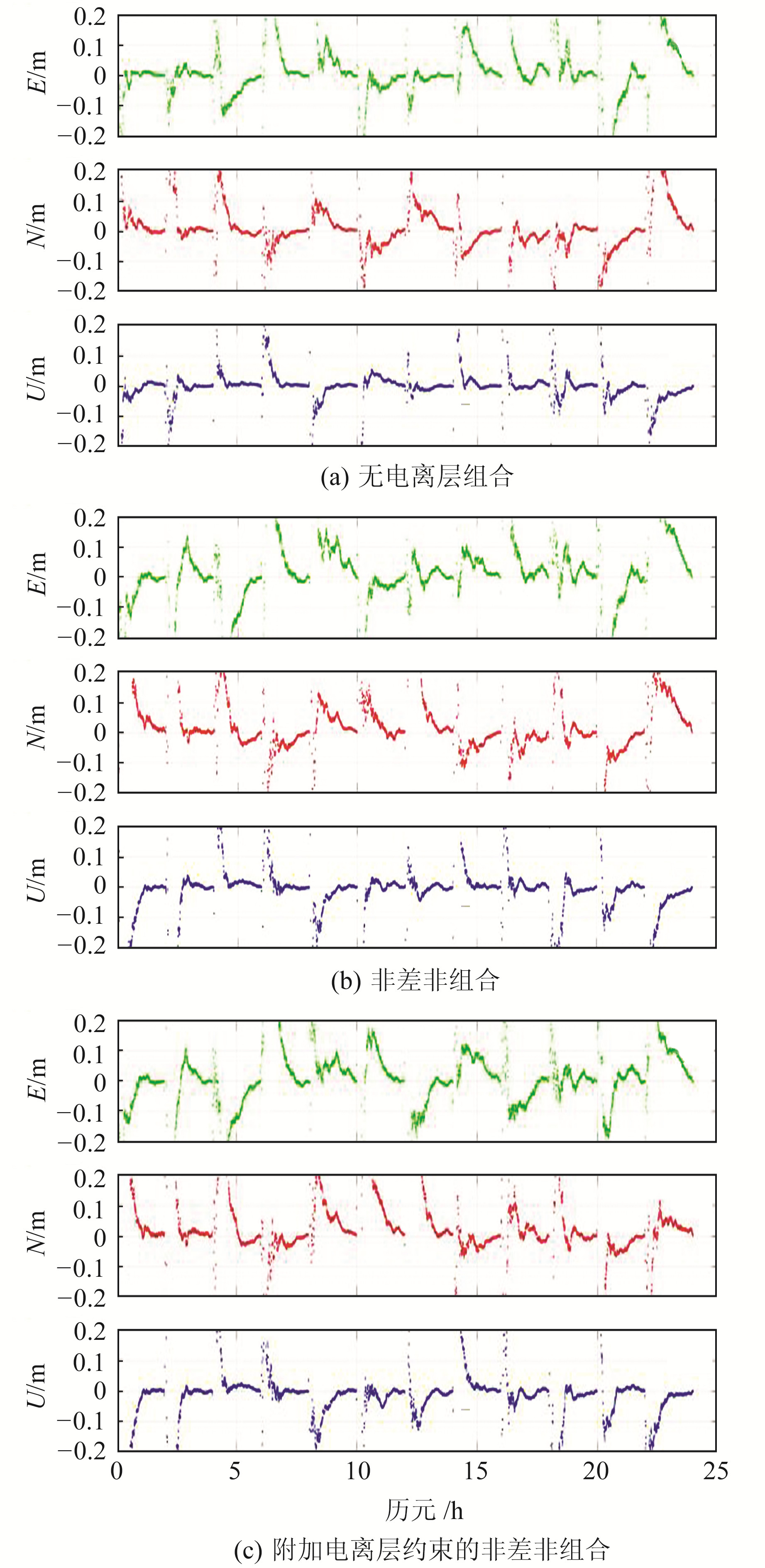
将1 d分为12个时段,每隔2 h进行一次卡尔曼滤波重置,并统计各个时段的PPP定位平均收敛时间(以参考站ALTH为例),进而对比分析附加电离层约束算法在多时段下的收敛性能。
由图 2可以看出,3种PPP定位算法在不同时段下的收敛速度不尽相同,其中无电离层组合方式和非差非组合方式收敛趋势基本一致,某些时段甚至费时长于60 min,PPP定位精度才能收敛至0.1 m;可以明显看出,附加电离层约束的非差非组合方式的PPP定位收敛更加快速。
|
图 2 3种算法在多时段下的PPP收敛过程 Fig. 2 Convergence process of PPP under multi-period with three arithmetics |
由表 1可以看出,3种不同PPP定位算法的定位精度基本一致,只是未附加电离层约束的非差非组合算法相较于附加电离层算法定位精度略低,主要原因是电离层延迟误差未得到更加有效的处理。
|
|
表 1 PPP定位结果 Tab. 1 PPP positioning results |
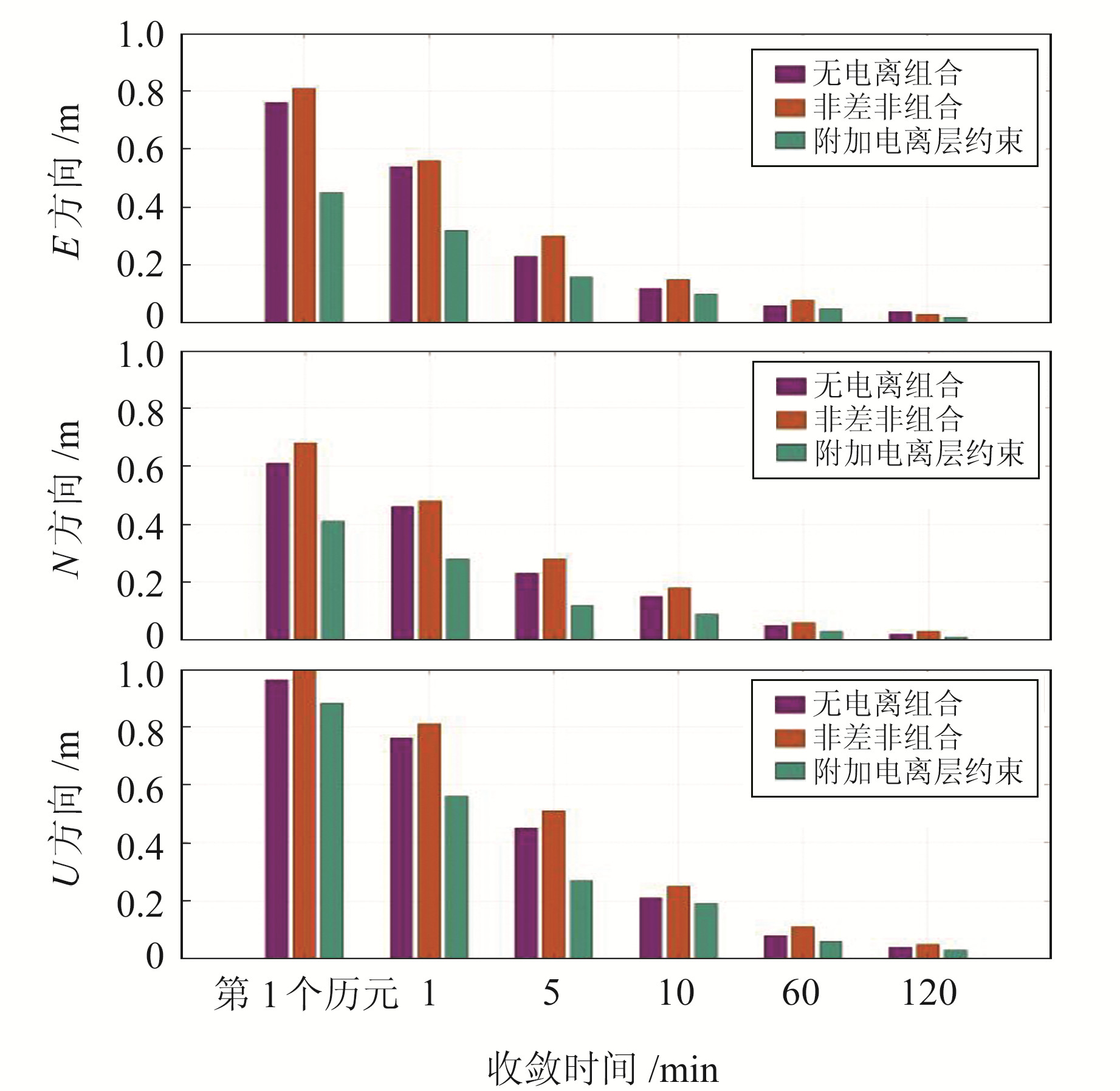
为了进一步分析附加电离层约束的非差非组合算法的收敛性能,分别统计了E、N、U三个坐标方向在不同时间下的PPP定位收敛精度(图 3)。
|
图 3 3个方向不同时段下的PPP定位精度 Fig. 3 PPP positioning accuracy at different time periods in three directions |
由图 3可以看出,在前10 min内,相比于无电离层组合和非差非组合算法,附加电离层约束算法的PPP定位结果收敛速度明显更快。与非差非组合算法相比,1 min时,对于E方向分量,加入电离层约束后,PPP定位精度从0.56 m提升到0.32 m,提高将近42.86%;对于N方向分量,PPP定位精度从0.48 m提升到0.28m,提高将近41.7%;对于U方向分量,PPP定位精度从0.81 m提升到0.56 m,提高将近30.86%。10 min后,3种算法收敛速度渐趋平稳,附加电离层约束算法优势表现不再显著。
PPP定位模型的几何强度可以通过卡尔曼滤波过程估计参数的协方差矩阵的迹来表现。图 4以参考站ALTH为例,显示了非差非组合和附加电离层约束的非差非组合两种算法估计参数的协方差矩阵迹的差值。

|
图 4 参数协方差矩阵迹的差值估计 Fig. 4 Estimated the difference of trace of parameter covariance matrix |
因为PPP观测模型中增加了电离层延迟虚拟观测量,该虚拟观测量的观测值为区域电离层延迟模型的计算值,虚拟观测值的方差为区域电离层延迟模型的先验方差。电离层延迟虚拟观测量为电离层延迟估计参数近似值,等于区域电离层延迟模型的计算值,因此观测方程的近似值与观测值差值为0。
通过增加电离层延迟虚拟观测方程,从而加强了观测模型的几何强度。累加虚拟观测方程后得到法方程,其法方程系数矩阵的对角元素值变大。对法方程系数矩阵求逆,得到待估参数的协方差矩阵。附加电离层延迟虚拟观测值后,待估参数的协方差矩阵对角元素值将变小,估计参数的方差变小,估计精度提高,待估参数的协方差矩阵对角元素值即代表了DOP值。对角元素之和为广义的GDOP(含电离层延迟参数和对流层湿延迟参数方差),也为协方差矩阵的迹。待估参数协方差矩阵对角元素值越小,DOP值越小,几何强度越高。
由图 4可明显看出,附加电离层约束的观测模型,其估计参数的协方差矩阵的迹在收敛初期显著变小,说明附加电离层延迟虚拟观测方程后,待估参数的精度在收敛初期提升明显。表 1的PPP定位误差显示,附加电离层约束的PPP定位误差在收敛初期显著小于消电离层组合PPP和非组合PPP,说明PPP定位误差与待估定位参数的精度信息一致。结果表明,附加电离层约束算法可以加强PPP定位模型的几何强度,进而加快收敛速度。
3 结语本文针对精密单点定位技术收敛时间较长的问题,提出一种附加高精度区域电离层先验信息约束的方法,采用美国西海岸CORS网内的参考站观测数据,进行区域电离层建模,获取高精度电离层先验信息,并且通过实际观测数据进行算法实验,得到以下结论:
1) 非差非组合和附加电离层约束的非差非组合两种算法的定位精度基本一致。
2) 相对于无电离层组合方式,非差非组合方式具有更小的观测噪声。
3) 在附加有效电离层信息后,非差非组合方式可以提高定位模型的几何强度,在PPP定位收敛过程中不同程度地提高收敛速度,在PPP定位开始的几分钟内表现尤为显著。
| [1] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1 399-1 407 (Zhang Xiaohong, Li Xingxing, Li Pan. Review of GNSS PPP and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 399-1 407)
(  0) 0) |
| [2] |
宋超, 郝金明, 张鹤. 利用先验对流层延迟约束加快PPP重新收敛方法[J]. 测绘科学技术学报, 2015, 32(5): 441-444 (Song Chao, Hao Jinming, Zhang He. A Method to Accelerate PPP Re-Convergence with Prior Troposphere Delay Constraint[J]. Journal of Geomatics Science and Technology, 2015, 32(5): 441-444)
(  0) 0) |
| [3] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉: 武汉大学, 2013 (Li Xingxing. Research on GNSS Precision Single Point Positioning and Non-Differential Ambiguity Fast Determination Method[D]. Wuhan: Wuhan University, 2013)
(  0) 0) |
| [4] |
Li X X, Ge M R, Zhang H P, et al. A Method for Improving Uncalibrated Phase Delay Estimation and Ambiguity-Fixing in Real-Time Precise Point Positioning[J]. Journal of Geodesy, 2013, 87(5): 405-416 DOI:10.1007/s00190-013-0611-x
(  0) 0) |
| [5] |
Cheng S, Zhou P, Wang J, et al. Enhancing Precise Point Positioning with External Ionosphere Constraints[C]. IGNSS Symposium, 2015
(  0) 0) |
| [6] |
王健, 党亚民, 王虎, 等. 多系统融合全球电离层建模研究[J]. 测绘通报, 2018(6): 7-11 (Wang Jian, Dang Yamin, Wang Hu, et al. Research on Multisystem Fusion Global Ionospheric Modeling[J]. Bulletin of Surveying and Mapping, 2018(6): 7-11)
(  0) 0) |
| [7] |
袁运斌. 基于GPS的电离层监测及延迟改正理论与方法的研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2002 (Yuan Yunbin. Research on the Theory and Method of Ionospheric Monitoring and Delay Correction Based on GPS[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2002)
(  0) 0) |
| [8] |
Hatch R. The Synergism of GPS Code and Carrier Measurements[J]. IGSS, 1983(2): 1 213-1 231
(  0) 0) |
| [9] |
蔡昌盛, 李征航, 赵晓峰. 利用GPS组合观测值建立区域电离层模型研究[J]. 测绘工程, 2003, 12(1): 13-16 (Cai Changsheng, Li Zhenghang, Zhao Xiaofeng. Study on Regional Ionospheric Model Using GPS Combination Observations[J]. Engineering of Surveying and Mapping, 2003, 12(1): 13-16)
(  0) 0) |
| [10] |
党亚民, 王虎, 赵文娇, 等. 融合BDS/GPS/GLONASS反演全球电离层特性研究[J]. 大地测量与地球动力学, 2015, 35(1): 87-91 (Dang Yamin, Wang Hu, Zhao Wenjiao, et al. Research of the Characteristics of Inversing Global Ionospheric with Fusing of BDS, GPS and GLONASS[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 87-91)
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China;
3. School of Geomatics, Liaoning Technical University, 188 South-Longwan Street, Fuxin 123000, China
 2021, Vol. 41
2021, Vol. 41


