2. 中国科学技术大学计算机科学与技术学院, 合肥市金寨路96号, 230088
北斗系统融合了导航与通信功能,具备定位导航授时、星基增强、地基增强、精密单点定位、短报文通信和国际搜救等多种服务能力[1-3]。其中,精密单点定位利用PPP-B2b信号作为数据播发通道,通过北斗3号GEO卫星播发北斗3号系统和其他全球卫星导航系统(GNSS)精密轨道和钟差等改正参数,为我国及周边地区用户提供动态dm级、静态cm级的精密定位服务[4-5]。目前,PPP-B2b已经能够播发有效卫星为C19~C45(C31除外)共26颗北斗3号卫星的精密改正电文。本文利用北斗系统播发的PPP-B2b信号数据,分析其在中国区域的静态和动态精密单点定位精度。
1 PPP定位模型与数据处理双频PPP数据处理时,通常利用无电离层组合消除电离层一阶项影响,伪距和相位无电离层组合观测方程可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {P_{{\rm{IF}}}^{S,i} = \rho + c\Delta {t^i} - c\Delta {t_{r,S}} + \delta {\rm{Trop + }}\varepsilon ({\rm{P}}_{{\rm{IF}}}^{{\rm{S}},{\rm{i}}})}\\ {\Phi _{{\rm{IF}}}^S = \rho + c\Delta {t^i} - c\Delta {t_{r,S}} + \delta {\rm{Trop + }}{\lambda _{\rm{i}}}{{\rm{N}}^{\rm{i}}}{\rm{ + }}\varepsilon (\Phi _{{\rm{IF}}}^{S,i})} \end{array}} \right. $ | (1) |
式中,S为卫星系统,i为卫星编号,PIFS, i、ΦIFS, i分别为无电离层伪距和相位观测值,ρ为包含卫星轨道误差、相对论效应、固体潮、天线相位中心等误差影响的站星几何距离,c为光速,Δti为卫星钟差,Δtr, S为接收机钟差,δTrop为对流层延迟,λi为无电离层组合波长,N为载波相位模糊度,ε(PIFS, i)、ε(ΦIFS, i)分别为伪距和相位多路径效应误差及观测噪声。
如何改正式(1)中卫星轨道、卫星钟差和码间偏差是实现高精度定位的关键和基础。利用北斗广播星历改正时,其改正精度有限,仅能获得dm~m级的定位精度[5]。北斗系统PPP-B2b信号旨在提供高精度的卫星轨道、钟差和码间偏差修正产品,提高卫星轨道、钟差和码间偏差的改正精度,显著提高北斗系统的定位服务性能。利用PPP-B2b改正卫星轨道、钟差及码间偏差方法如下。
1.1 卫星轨道改正轨道改正信息参数为轨道改正向量δO在径向、切向和法向的分量,联合利用广播星历计算出的卫星位置向量Xbroadcast可计算卫星位置改正向量δX。修正算法如下:
| $ {\mathit{\boldsymbol{X}}_{{\rm{orbit}}}} = {\mathit{\boldsymbol{X}}_{{\rm{broadcast}}}} - \delta \mathit{\boldsymbol{X}} $ | (2) |
式中,Xorbit为改正后的卫星位置,Xbroadcast为广播星历计算得到的卫星位置,δX为轨道改正数。δX的计算公式为:
| $ \begin{array}{l} {\mathit{\boldsymbol{e}}_{{\rm{radial}}}} = \frac{\mathit{\boldsymbol{r}}}{{|\mathit{\boldsymbol{r}}|}}\\ {\mathit{\boldsymbol{e}}_{{\rm{cross}}}} = \frac{{r \times \dot r}}{{|r \times \dot r|}}\\ {\mathit{\boldsymbol{e}}_{{\rm{along}}}} = {\mathit{\boldsymbol{e}}_{{\rm{cross}}}} \times {\mathit{\boldsymbol{e}}_{{\rm{radial}}}}\\ \delta \mathit{\boldsymbol{r}} = [{\mathit{\boldsymbol{e}}_{{\rm{radial}}}}\;\;{\mathit{\boldsymbol{e}}_{{\rm{along}}}}\;\;{\mathit{\boldsymbol{e}}_{{\rm{cross}}}}]\cdot\;\delta \mathit{\boldsymbol{O}} \end{array} $ | (3) |
式中,r、
钟差改正电文参数是相对于广播星历钟差的改正参数:
| $ {t_{{\rm{satellite}}}} = {t_{{\rm{broadcast}}}} - \frac{{{C_0}}}{c} $ | (4) |
式中,tbroadcast为广播星历计算得到的卫星钟差改正数,tsatellite为改正后的卫星钟差改正数,C0为PPP-B2b提供的钟差改正参数。
1.3 卫星码间偏差修正由于卫星跟踪模式的不同,各观测值都包含一个与信号跟踪模式相关的偏差。同步处理各频率的各类信号时,首先需要消除该偏差,其修正算法为:
| $ {\tilde P_{{\rm{sig}}}} = {P_{{\rm{sig}}}} - {\rm{DC}}{{\rm{B}}_{{\rm{sig}}}} $ | (5) |
式中,
本文选取2020年doy 112~115的B2b改正数产品,以GBM事后最终轨道和钟差产品为基准,分析比较B2b精密轨道和钟差产品的精度,计算方法详见参考文献[5]。表 1给出B2b实时产品的轨道在径向(R)、切向(A)、法向(C)差值的RMS值,以及钟差的RMS和STD值。可以看出,B2b产品轨道R方向精度均值为0.07 m,A方向精度均值为0.33 m,C方向精度均值为0.24 m;钟差存在约4~5 ns的系统差,但是STD值优于0.10 ns,能满足cm~dm级实时定位精度需求。
|
|
表 1 B2b轨道钟差产品精度统计 Tab. 1 Accuracy statistics of B2B track clock error products |
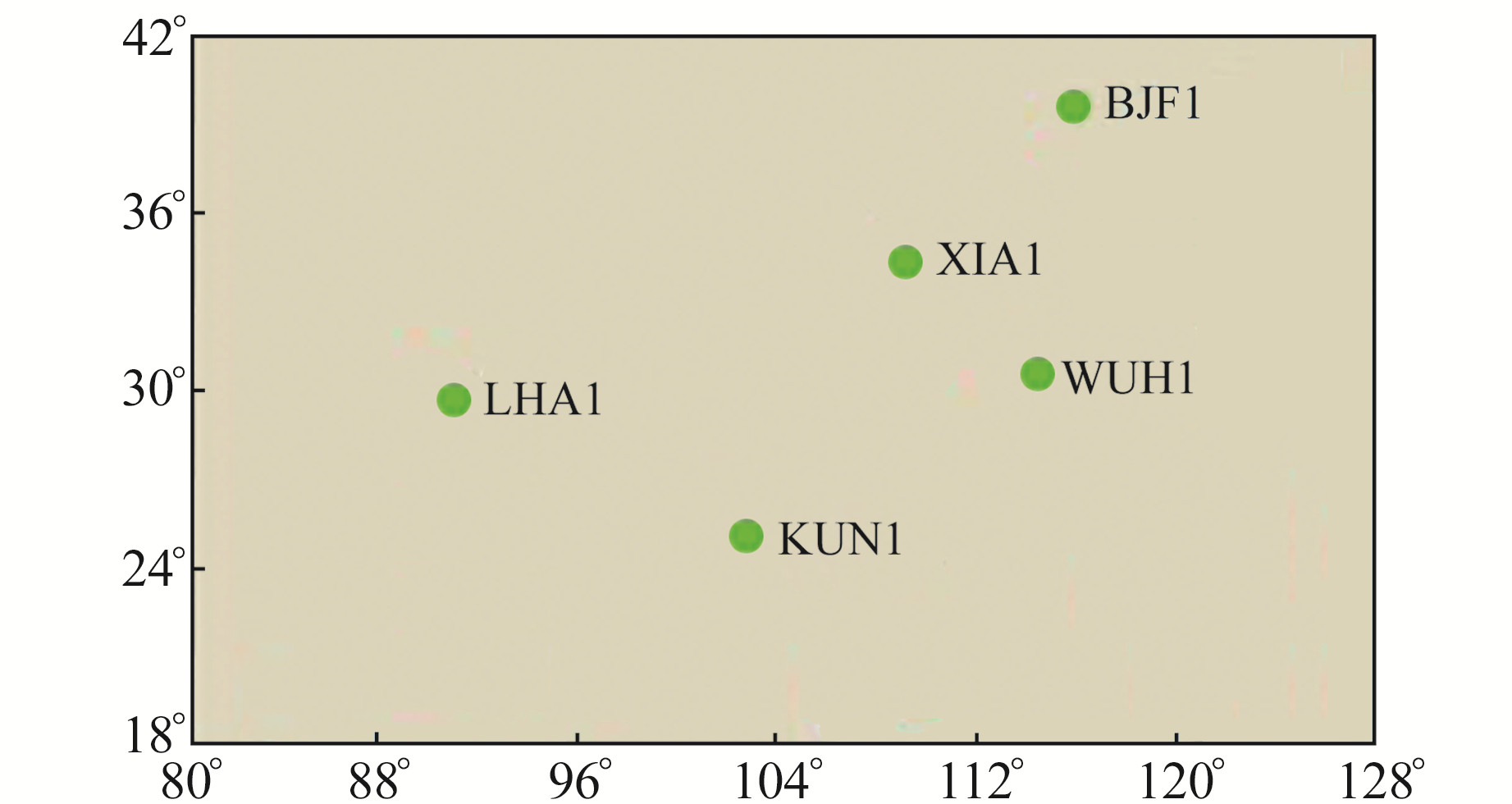
为验证北斗3号PPP-B2b卫星轨道、钟差及码间偏差产品的服务性能,选取IGMAS中国区域的BJF1、LHA1、KUN1、WUH1、XIA1等5个测站在2020年doy 112~115的观测数据,利用实时收到的北斗3号PPP-B2b电文信息,分别通过式(2)~(4)改正卫星轨道、钟差和码间偏差,采用事后仿实时静态、动态PPP定位精度分析,将定位结果与真值坐标进行比较,其中真值坐标由周解坐标提供。图 1为测站分布。
|
图 1 测站分布 Fig. 1 Distribution of stations |
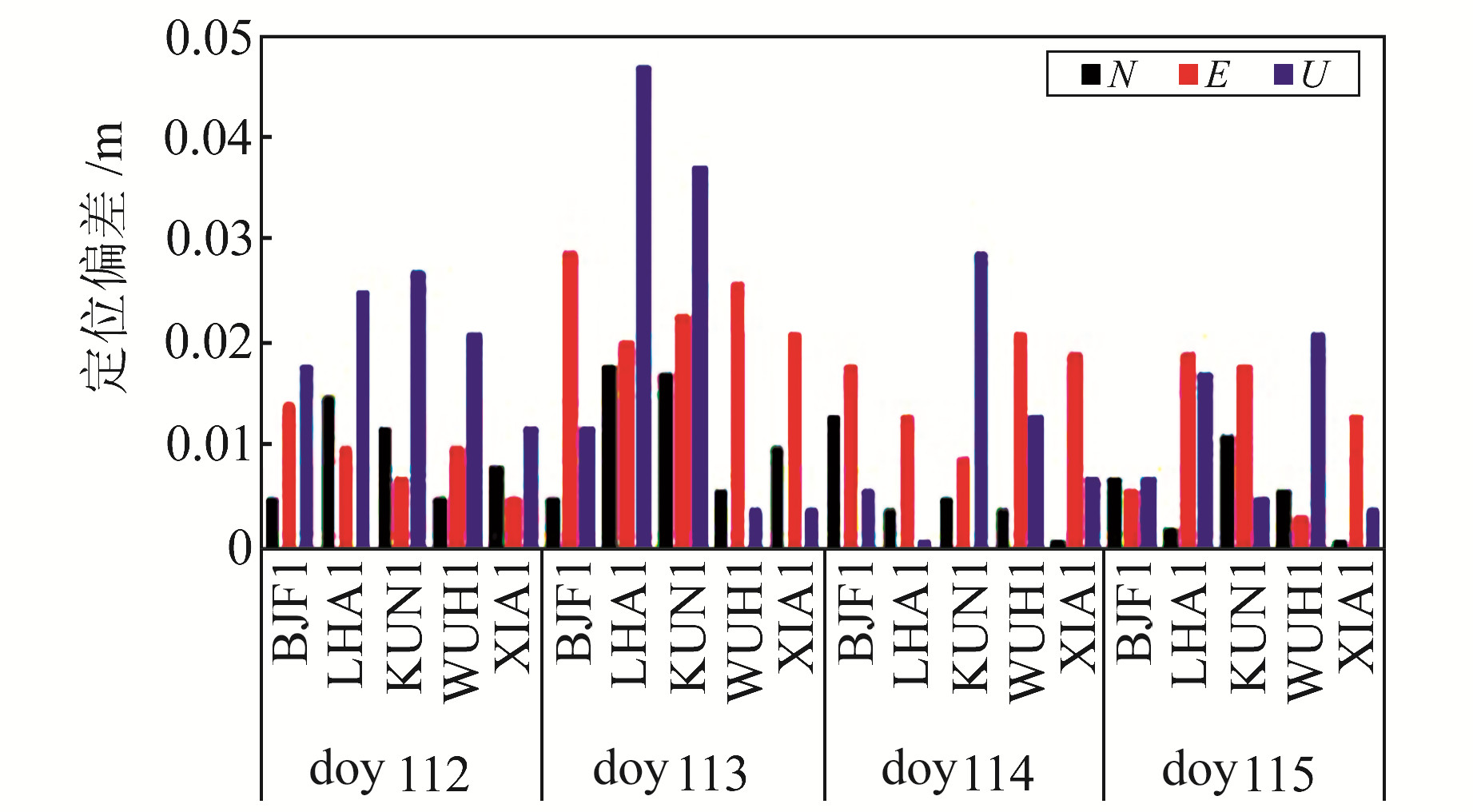
将各测站数据进行24 h静态解算,比较最终定位坐标结果与真值坐标,分别统计各测站所能达到的定位精度(图 2)。
|
图 2 静态定位精度统计 Fig. 2 Static positioning accuracy statistics |
由图 2可见,各测站N、E方向定位精度均优于3 cm,高程方向优于5 cm。将各测站4 d的定位精度取平均值,如表 2(单位m)所示。可以看出,利用北斗3号PPP-B2b信号提供的精密卫星轨道、钟差及码间偏差产品的静态PPP定位精度可达0.8 cm、1.5 cm、1.6 cm。
|
|
表 2 各测站静态定位精度均值 Tab. 2 Mean values of static positioning accuracy of each station |
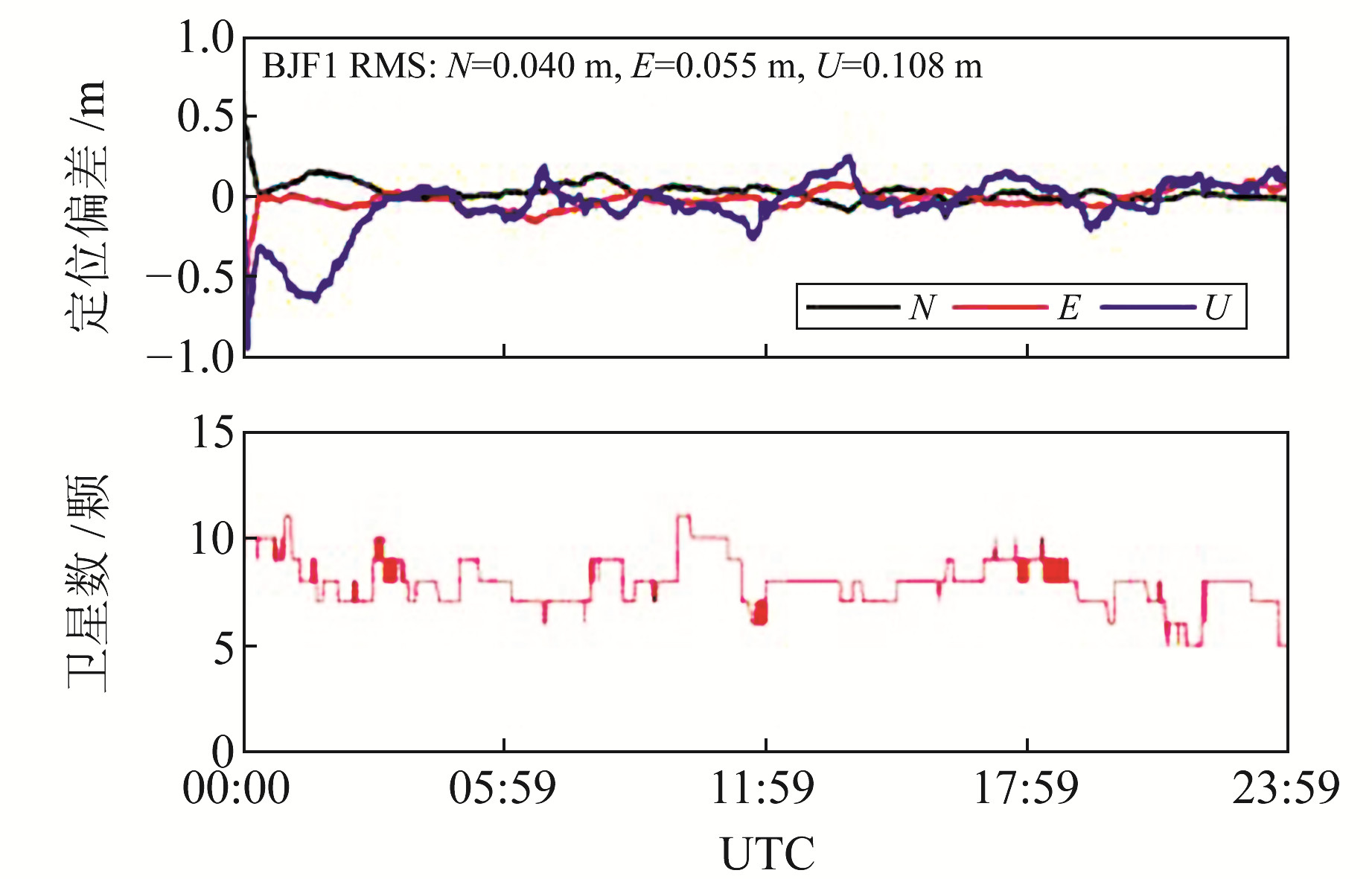
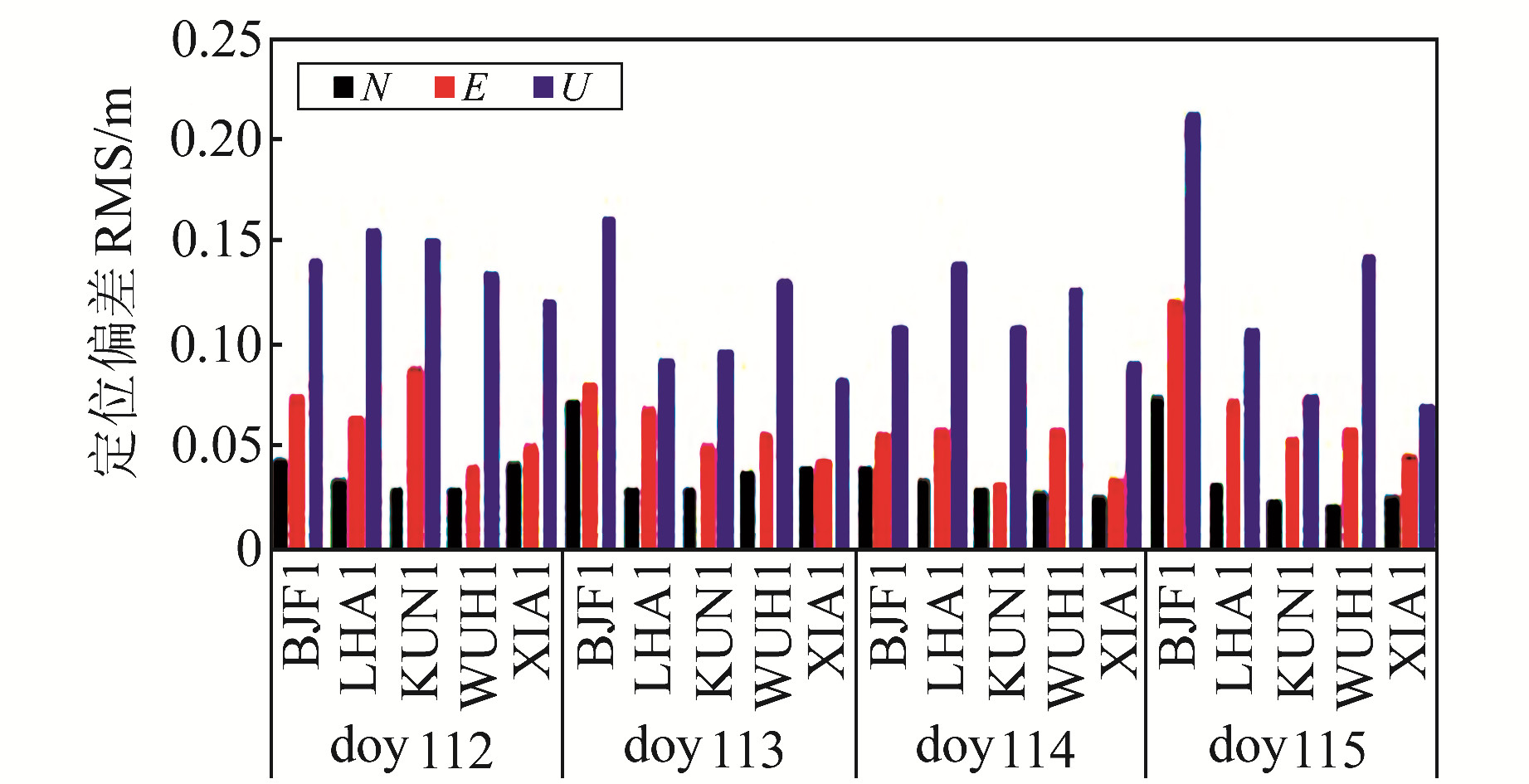
图 3给出BJF1站2020年doy 114动态PPP定位偏差和卫星数时间序列。可以看出,目前在中国区域BDS-3可用卫星数约为7~12颗,动态PPP收敛后N、E、U方向定位精度RMS分别为4.0 cm、5.5 cm和10.8 cm。图 4给出4 d内各测站的定位精度RMS统计。可以看出,除BJF1测站外,其他测站4 d内定位精度RMS平面方向均优于10 cm、高程方向优于20 cm,且不同测站没有明显的精度差异,说明不同天北斗3号PPP-B2b信号定位精度稳定,且不同区域的定位精度相当。进一步将各测站4 d的定位精度取平均,如表 3(单位m)所示,作为对比,表 3也给出了采用GBM事后产品动态定位精度的RMS统计。可以看出,采用GBM事后最终产品,动态PPP定位精度平均RMS在N、E、U方向分别达到2.3 cm、3.3 cm和9.2 cm;而利用北斗3号PPP-B2b信号,动态PPP定位精度N、U方向比GBM稍低,E方向明显比GBM低,N、E、U方向平均RMS分别达到3.6 cm、6.0 cm和12.2 cm。
|
图 3 2020年doy114定位偏差及卫星数的时间序列 Fig. 3 Time series of doy 114 positioning deviation and satellite number in 2020 |
|
图 4 2020年doy112~115定位偏差统计 Fig. 4 Statistics of positioning deviation during doy 112 to 115 in 2020 |
|
|
表 3 B2b产品动态定位精度RMS统计 Tab. 3 RMS statistics of dynamic positioning accuracy of B2B products |
根据北斗3号B2b信号精度指标,本文以平面定位精度优于0.3 m、高程定位精度优于0.6 m所需要的时间作为PPP收敛时间,给出各测站2020年doy 112~115的平均收敛时间(见表 4,单位s)。由表可知,B2b约需要0.5 h的收敛时间,除BJF1站外,其他测站的收敛时间比GBM稍长。
|
|
表 4 测站收敛时间统计 Tab. 4 Convergence time statistics |
本文选取iGMAS中国区域的BJF1、LHA1、KUN1、WUH1、XIA1等5个测站2020年doy 112~115观测数据对北斗3号PPP-B2b信号定位效果进行分析,结果表明,在我国区域内,利用北斗3号PPP-B2b信号,静态PPP定位N、E、U方向定位精度RMS分别可达0.8 cm、1.5 cm和1.6 cm,动态定位精度RMS分别达到3.6 cm、6.0 cm和12.2 cm,实现了静态cm级、动态dm级的定位服务,达到系统设计的指标要求。
| [1] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5 005-5 017 DOI:10.1029/96JB03860
(  0) 0) |
| [2] |
Kouba J. Measuring Seismic Waves Induced by Large Earthquakes with GPS[J]. Studia Geophysica et Geodaetica, 2003, 47(4): 741-755 DOI:10.1023/A:1026390618355
(  0) 0) |
| [3] |
Guo J, Li X X, Li Z H, et al. Multi-GNSS Precise Point Positioning for Precision Agriculture[J]. Precision Agriculture, 2018, 19(5): 895-911 DOI:10.1007/s11119-018-9563-8
(  0) 0) |
| [4] |
朱永兴, 冯来平, 贾小林, 等. 北斗区域导航系统的PPP精度分析[J]. 测绘学报, 2015, 44(4): 377-383 (Zhu Yongxing, Feng Laiping, Jia Xiaolin, et al. The PPP Precision Analysis Based on BDS Regional Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 377-383)
(  0) 0) |
| [5] |
施闯, 郑福, 楼益栋. 北斗广域实时精密定位服务系统研究与评估分析[J]. 测绘学报, 2017, 46(10): 1 354-1 363 (Shi Chuang, Zheng Fu, Lou Yidong. Research and Evaluation of BDS Real-Time Wide-Area Precise Positioning Service System[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 354-1 363)
(  0) 0) |
2. School of Computer Science and Technology, University of Science and Technology of China, 96 Jinzhai Road, Hefei 230088, China
 2021, Vol. 41
2021, Vol. 41


