2. 福州市勘测院, 福州市高新大道1号, 350108;
3. 河南城建学院测绘与城市空间信息学院, 河南省平顶山市龙翔大道, 467036
快速准确地固定整周模糊度是载波相位测量的关键技术,目前应用最广的模糊度解算方法是基于整数最小二乘估计的模糊度降相关平差法(LAMBDA算法)[1]。由于在轨卫星的数量逐渐增多,导致模糊度解算的维数不断增加,而现有的模糊度解算方法在解算高维模糊度时效率较低[2],因此如何有效提升高维模糊度的解算效率成为国内外学者的主要研究内容[3-11]。卢立果等[5]提出一种基于下三角Cholesky分解的整数高斯变换算法(low-triangular Cholesky decomposition integer Gauss transformation, LIGT),该算法与LAMBDA算法等价,是LAMBDA算法在下三角Cholesky分解下的一种补充。本文在LIGT算法的基础上进行改进,以提高LIGT算法在高维情况下的降相关效率。
1 MLIGT算法MLIGT算法(modified low-triangular Cholesky decomposition integer Gauss transformation, MLIGT)是本文在LIGT算法基础上进行改进的一种快速降相关算法,基于下列2个改进策略,可以有效提高LIGT算法的降相关效率以及总体效率。
1.1 改进策略1改进策略1是在进行整数高斯变换之前,使用对称旋转排序策略对条件方差仅进行一次预排序。利用该策略可以减少条件方差的交换次数,从而提高算法的运行效率。
假设协方差矩阵
| $ {\mathit{\boldsymbol{Q}}_{\hat a\hat a}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{q}}_{11}}&\mathit{\boldsymbol{q}}\\ {{\mathit{\boldsymbol{q}}^{\rm{T}}}}&{{{\mathit{\boldsymbol{\tilde Q}}}_{\hat a\hat a}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{}\\ \mathit{\boldsymbol{l}}&{\mathit{\boldsymbol{\tilde L}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{d}}1}&{}\\ {}&{\mathit{\boldsymbol{\tilde D}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&{{\mathit{\boldsymbol{l}}^{\rm{T}}}}\\ {}&{{{\mathit{\boldsymbol{\tilde L}}}^{\rm{T}}}} \end{array}} \right] $ | (1) |
由式(1)可得,d1=q11,q=d1lT,
对称旋转策略首先找到协方差矩阵
| $ {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{Q}}_{\hat a\hat a}}\mathit{\boldsymbol{P}}_1^{\rm{T}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{q}}_{11}}}&\mathit{\boldsymbol{q}}\\ {{\mathit{\boldsymbol{q}}^{\rm{T}}}}&{{{\mathit{\boldsymbol{\tilde Q}}}_{\hat a\hat a}}} \end{array}} \right] $ | (2) |
令d1=q11、
| $ \mathit{\boldsymbol{\tilde P}}\left( {{{\mathit{\boldsymbol{\tilde Q}}}_{\hat a\hat a}} - \mathit{\boldsymbol{l}}{\mathit{\boldsymbol{d}}_1}{\mathit{\boldsymbol{l}}^{\rm{T}}}} \right){{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}{\rm{ = }}\mathit{\boldsymbol{\tilde L\tilde D}}{{\mathit{\boldsymbol{\tilde L}}}^{\rm{T}}} $ | (3) |
式中,
| $ \begin{array}{l} {{\mathit{\boldsymbol{\bar Q}}}_{\hat a\hat a}} = \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{Q}}_{\hat a\hat a}}{\mathit{\boldsymbol{P}}^{\rm{T}}} = \mathit{\boldsymbol{LD}}{\mathit{\boldsymbol{L}}^{\rm{T}}}, \mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{P}}_1}\left[ {\begin{array}{*{20}{c}} 1&{}\\ {}&{\mathit{\boldsymbol{\tilde P}}} \end{array}} \right], \\ \;\;\;\;\;\mathit{\boldsymbol{L = }}\left[ {\begin{array}{*{20}{c}} 1&{}\\ {\mathit{\boldsymbol{l}}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}}&{\mathit{\boldsymbol{\tilde L}}} \end{array}} \right], \mathit{\boldsymbol{D = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{d}}_1}}&{}\\ {}&{\mathit{\boldsymbol{\tilde D}}} \end{array}} \right] \end{array} $ | (4) |
LIGT算法有2次整数高斯变换(即元素降相关)过程,第1次整数高斯变换是对L矩阵次对角线元素进行高斯消去,第2次是在满足交换条件后对L矩阵剩余的元素进行高斯消去。由于条件方差交换的影响,可能会造成第1次整数高斯变换和第2次整数高斯变换过程中部分元素重复执行,增加降相关耗时。为了解决这一问题,将第1次整数高斯变换过程与条件方差交换步骤进行合并,以此减少冗余的整数高斯变换过程,该策略本文称之为延后降相关。改进后算法的条件方差交换条件发生了改变:
| $ \begin{array}{*{20}{l}} {{d_i} + {{({l_{i, i - 1}} - [{l_{i, i - 1}}]{\rm{ }})}^2}{d_{i - 1}} < {d_{i - 1}}} \end{array} $ | (5) |
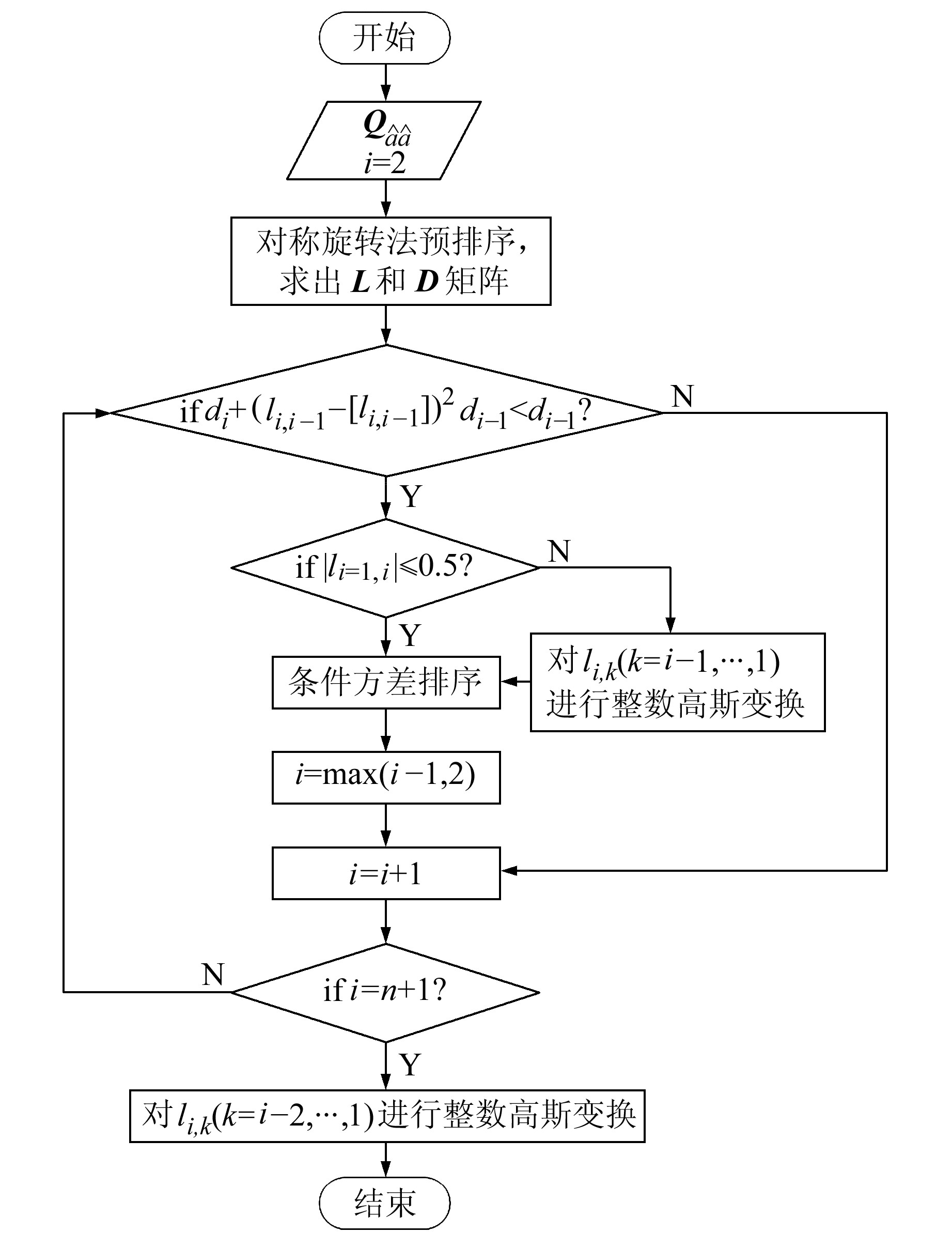
由于改进策略1增加了对称旋转策略预排序,改进策略2使用延后降相关策略将第1次降相关整合到条件方差交换过程之中,因此MLIGT算法相较于LIGT算法在程序流程上有了较大的改变。MLIGT算法流程如图 1所示,解算过程如下。
|
图 1 MLIGT算法流程 Fig. 1 MLIGT algorithm flowchart |
1) 输入原始协方差矩阵
2) 判断交换条件di+(li, i-1-[li, i-1])2di-1 < di-1是否成立,如果不成立,则更新i的值;如果成立,则继续判断li, i-1的绝对值是否大于0.5,如果大于0.5则先对li, k(k=i-1, …, 1)进行整数高斯变换,然后进行条件方差排序,如果小于等于0.5,则直接进行条件方差排序,最后更新i的值。
3) 判断i的值是否超过模糊度维数n,如果i小于n,则返回步骤2);如果i大于n,则进入第2次降相关,对li, k(k=i-2, …, 1)进行整数高斯变换,最后结束程序。
2 实验与分析分别设计模拟数据实验和实测数据实验对LIGT算法、SEQR算法以及MLIGT算法进行对比分析。实验使用的计算机配置为:Intel CORE i5-4210M处理器,8 G内存,Windows10系统。
2.1 模拟数据实验模拟数据根据文献[12]中的方法设计,浮点解构造方式为:
| $ \begin{array}{*{20}{l}} {\hat a = 100 \times {\rm{randn}}(n, 1)} \end{array} $ | (6) |
模糊度协方差矩阵
| $ {\mathit{\boldsymbol{Q}}_{\hat a\hat a}}{\rm{ = }}\begin{array}{*{20}{l}} {\mathit{\boldsymbol{U \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{U}}^{\rm{T}}}} \end{array} $ | (7) |
式中,U为单位正交矩阵,Λ为对角矩阵,服从[0, 1]均匀分布,且对Λ按照升序排列。U的构造形式为:
| $ \mathit{\boldsymbol{U}} = {\mathit{\boldsymbol{U}}_{n, n - 1}}{\mathit{\boldsymbol{U}}_{n, n - 2}}, {\rm{ }} \ldots {\rm{ }}, {\mathit{\boldsymbol{U}}_{n, 1}}, {\rm{ }} \ldots {\rm{ }}, {\mathit{\boldsymbol{U}}_{3, 1}}{\mathit{\boldsymbol{U}}_{2, 1}} $ | (8) |
其中,Ui, j的构造形式为:
| $ \begin{array}{l} {\mathit{\boldsymbol{U}}_{i, j}}{\rm{ = }}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{I}}_1}}&0&0&0&0\\ 0&{\cos {\theta _{i, j}}}&0&{\sin {\theta _{i, j}}}&0\\ 0&0&{{I_2}}&0&0\\ 0&{ - \sin {\theta _{i, j}}}&0&{\cos {\theta _{i, j}}}&0\\ 0&0&0&0&{{I_3}} \end{array}} \right], \\ \;\;\;\;\;\;\;\;\;\;\;\;\; - \frac{{\rm{ \mathsf{ π} }}}{2} \le {\theta _{i, j}} \le \frac{{\rm{ \mathsf{ π} }}}{2} \end{array} $ | (9) |
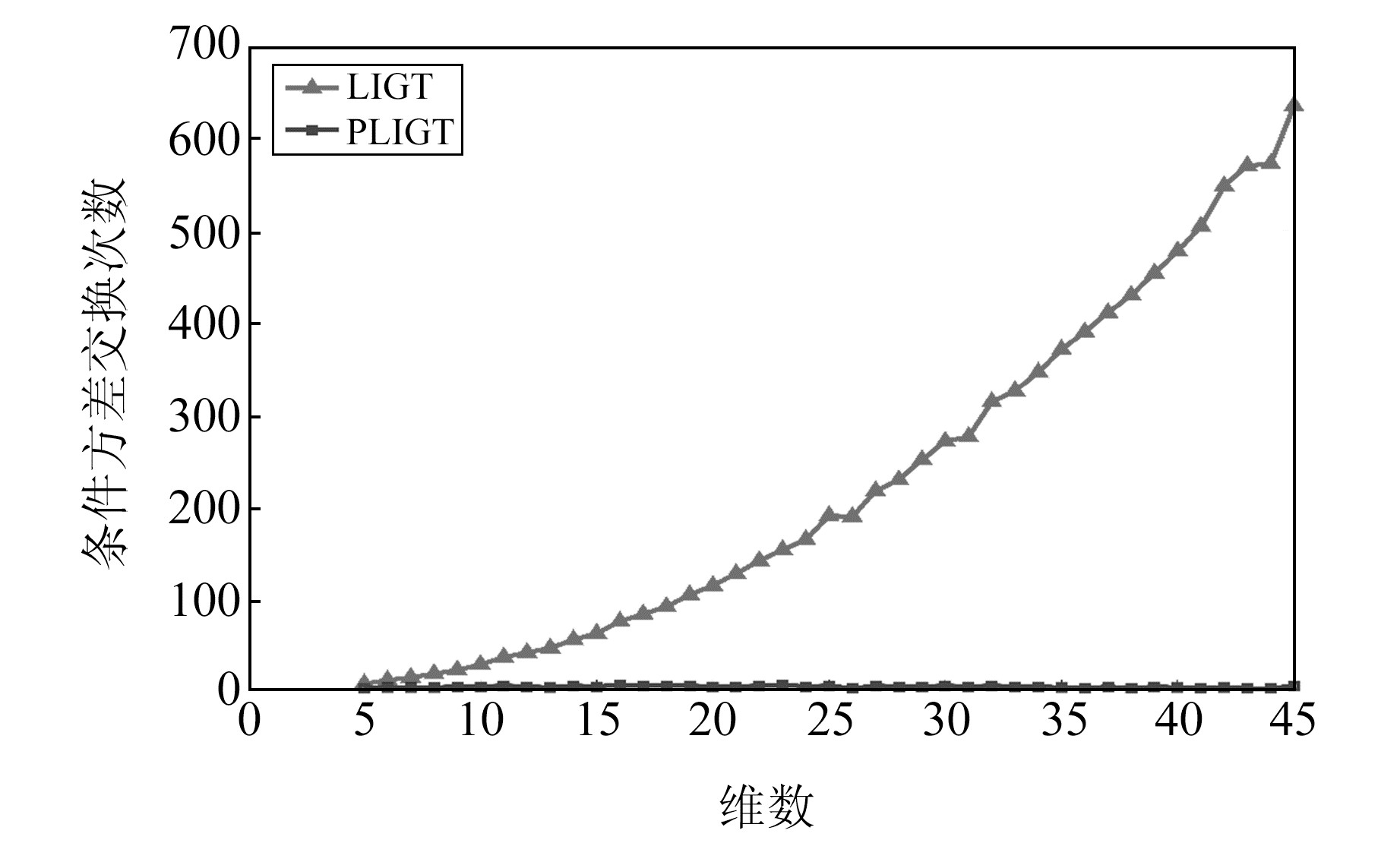
利用上述模拟方法,构建5~45维模糊度协方差矩阵,每一维度模拟100组数据。为了对比改进策略1对LIGT算法的提升,使用LIGT算法和PLIGT(permutational low-triangular Cholesky decomposition integer Gauss transformation)算法分别进行处理,其中PLIGT算法是仅在LIGT算法基础上增加了改进策略1。图 2是不同维度下2种算法的平均条件方差交换次数的变换规律。由图可见,随着维度的变化,LIGT算法的条件方差交换次数不断增加;而PLIGT算法的条件方差交换次数始终稳定在一个较低的水平,且明显低于LIGT算法。因此改进策略1通过减少条件方差交换次数,可以显著提高LIGT算法的解算效率。
|
图 2 不同维度下条件方差交换次数 Fig. 2 Numbers of conditional variance exchanges in different dimensions |
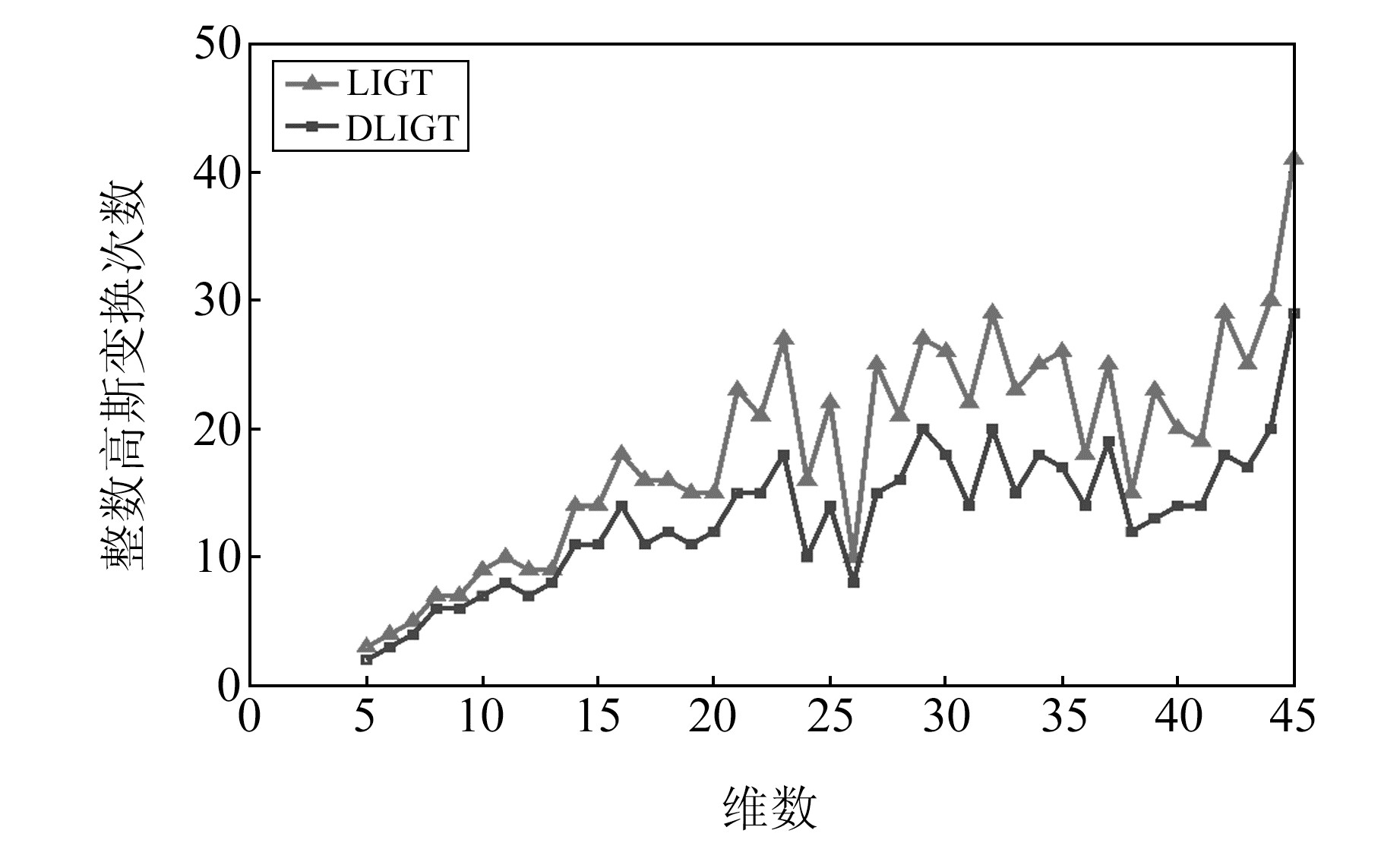
为了对比改进策略2单个因素对LIGT算法的提升,在LIGT算法基础上仅使用改进策略2设计出一个对比算法,命名为DLIGT(delayed low-triangular Cholesky decomposition integer Gauss transformation)算法。图 3为2种算法在不同维度下100组数据的平均整数高斯变换次数的结果对比,其中整数高斯变换次数指算法的第1次和第2次整数高斯变换的累积总次数。由图 4可见,随着维度的上升,2种算法的整数高斯变换次数整体呈现上升趋势,此外,DLIGT算法的平均整数高斯变换次数在不同维度下均低于LIGT算法。因此,改进策略2可以通过减少LIGT算法的整数高斯变换过程次数,在一定程度上提高算法的降相关效率。
|
图 3 不同维度下整数高斯变换次数 Fig. 3 Numbers of integer Gaussian transformations in different dimensions |
|
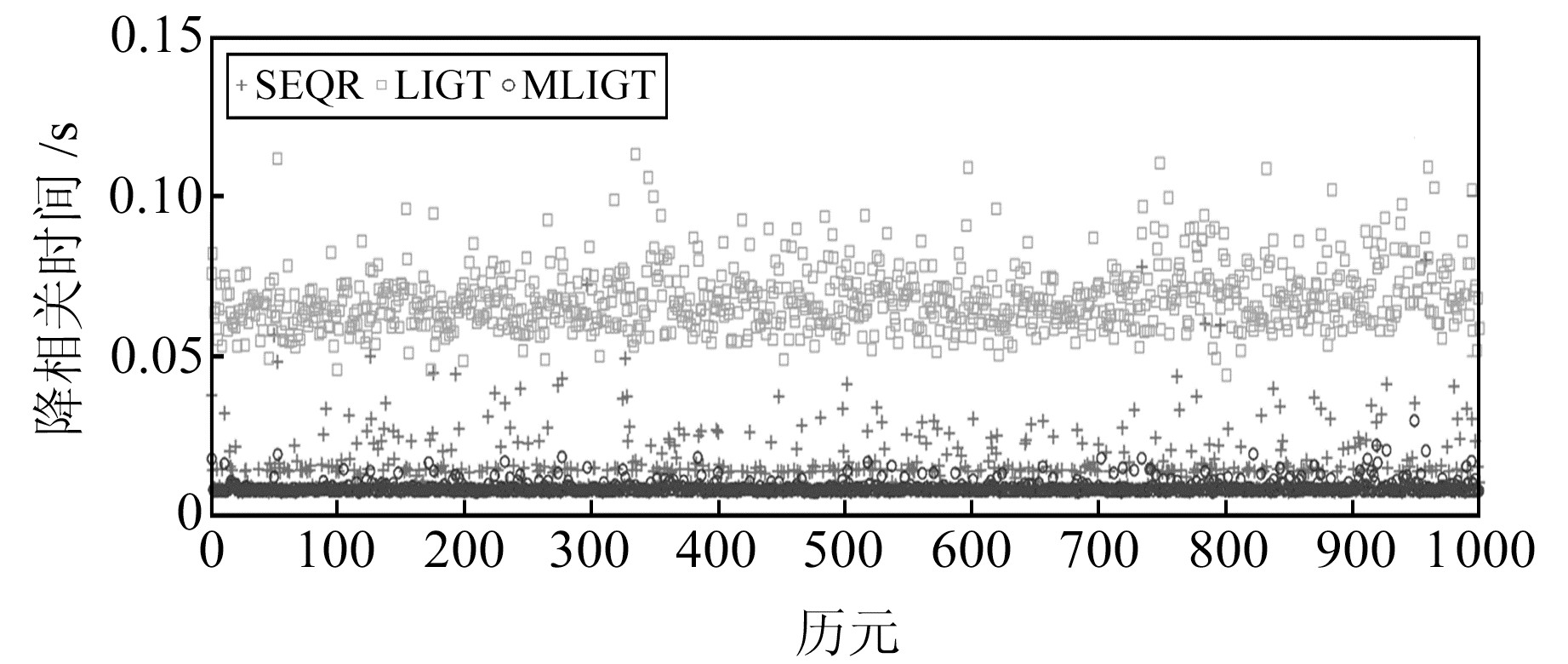
图 4 不同历元下40维模拟数据的降相关时间 Fig. 4 Decorrelation time of 40-dimensional simulation data in different epochs |
为了验证2个策略对LIGT算法的综合改进效果,使用上述模拟方法模拟1 000历元的模糊度数据,每个历元的模糊度矩阵维数为40。实验对比了SEQR算法、LIGT算法和MLIGT算法的降相关时间和降相关时间标准差,如表 1所示,不同历元下的降相关时间对比结果见图 4。从表 1和图 4的结果可以看出,MLIGT算法相较于LIGT算法效率有较大提升,比SEQR算法效率略高,此外MLIGT算法的时间稳定性在3种算法中表现最好。
|
|
表 1 模拟数据实验的平均降相关时间及其标准差 Tab. 1 The average decorrelation time and its standard deviation of the simulated data experiment |
为了进一步验证改进算法在实际测量中的效率以及解算时间的稳定性,采用SEQR算法、LIGT算法、MLIGT算法分别对实测的2组GNSS数据进行实验,对比3种算法的降相关时间、搜索时间、总体时间以及总体时间的标准差。其中,搜索方法同前面章节一致,使用基于LDLT分解的SE-VB算法。
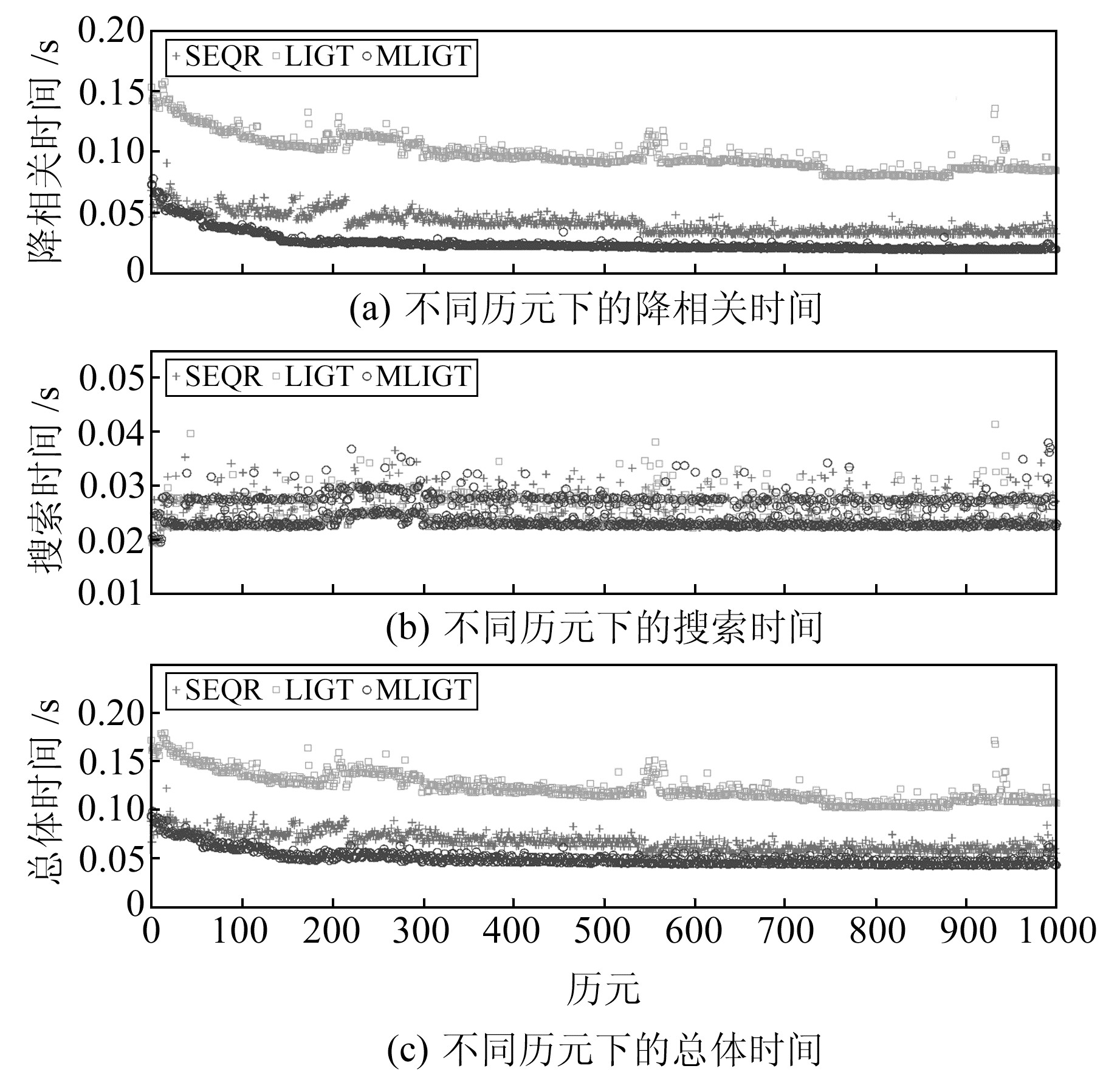
2.2.1 实验1第1组数据为静态观测数据,基线长为29.5 km,采样间隔为1 s,数据采集时观测环境开阔,数据质量良好,采用GPS+BDS单历元处理结果,取前1 000个历元进行实验,模糊度维数在40维左右。第1组数据的平均解算结果见表 2,不同历元下的解算时间见图 5。从表 2和图 5可以看出,MLIGT算法的降相关时间最小,SEQR算法次之,两者均比LIGT算法降相关效率高。3种算法的搜索时间差异不大,因此减少总体解算耗时的关键取决于降相关效率。从图 5也可以看出,3种算法的总体解算时间与降相关时间的图像线型趋势基本保持一致。从表 2可以看出,MLIGT算法总体时间标准差最小,因此在该组实验中MLIGT算法的解算时间稳定性比其他2种算法表现更好。
|
|
表 2 静态观测数据的平均解算时间和总体时间标准差 Tab. 2 Mean solution time and total time standard deviation of static observations |
|
图 5 不同历元下静态观测数据的模糊度解算时间 Fig. 5 Resolution time of ambiguity of static observation data under different epochs |
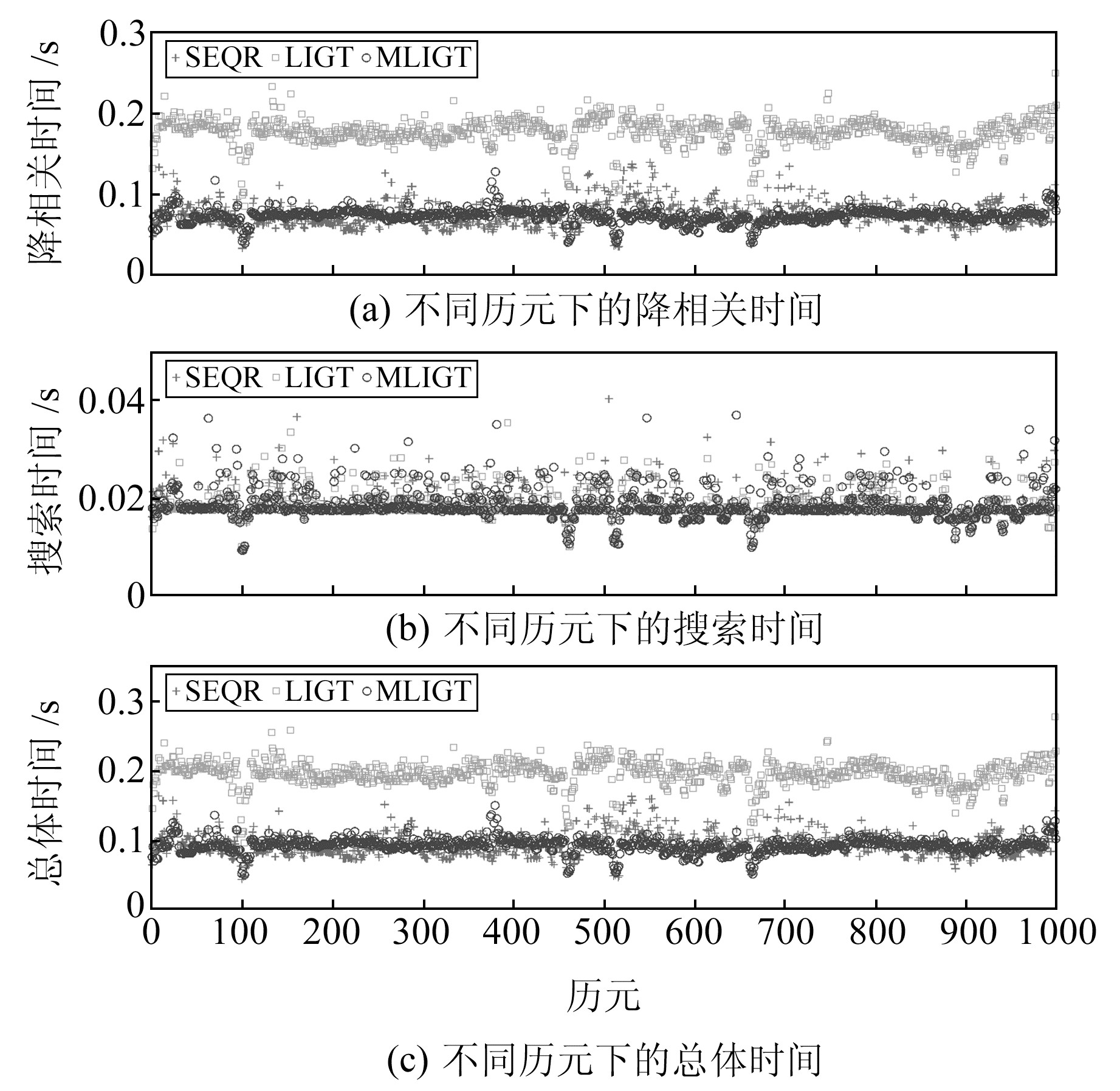
第2组数据为动态观测数据,该组数据为车载数据,基准站架设于开阔空地,流动站搭载在行驶车辆车顶上进行动态测量,采样间隔为1 s,观测数据采用GPS+BDS单历元处理结果,取前1 000个历元进行实验,模糊度维数在30~40之间。第2组数据的平均解算结果见表 3,不同历元下的模糊度解算时间见图 6。从表 3可以看出,MLIGT算法的平均降相关时间虽然在3者中最短,但与SEQR算法的平均降相关时间差距不是很明显。3种算法的搜索时间差异较小,因此3种算法总体解算时间的长短仍取决于降相关时间的长短。从总体时间标准差来看,MLIGT算法的标准差最小,因此理论上MLIGT算法的解算时间稳定性更好。从图 6(a)和6(c)也可以看出,MLIGT算法与SEQR算法虽然大部分线型基本重合,但MLIGT算法明显更向中心靠拢,而SEQR算法的线型则较为发散。
|
|
表 3 动态观测数据的平均解算时间和总体时间标准差 Tab. 3 Mean solution time and total time standard deviation of dynamic observation data |
|
图 6 不同历元下动态观测数据的模糊度解算时间 Fig. 6 Resolution time of ambiguity of dynamic observation data under different epochs |
通过模拟实验可以看出,MLIGT算法的改进策略1通过减少条件方差交换次数来提高降相关效率,改进策略2通过减少整数高斯变换次数来提高降相关效率。因此在2种改进策略的共同作用下,MLIGT算法的降相关效率得到较为显著的提升,并且随着维度的升高,2种策略的改进效果与LIGT算法相比会更显著。
通过综合模拟数据实验和2组实测数据实验的结果可以看出,MLIGT算法的整体解算效率明显高于LIGT算法,且维数在40及以上的实验组中,效率要高于SEQR算法。MLIGT算法与SEQR算法效率的高低取决于模糊度维数的大小和数据的构造,因为MLIGT算法相较于SEQR算法有一个条件方差交换过程,可以进一步对不满足升序排列的条件方差进行变换,而且MLIGT算法中的对称旋转排序只作一次,是在进入循环前进行一次排序;而SEQR算法的对称旋转排序过程不低于一次,排序的次数取决于维数的大小和数据的构造,通常在数据维数较大时,一次整数高斯变换可能无法跳出循环,需要继续循环进行对称旋转排序和整数高斯变换,直到满足元素降相关的条件而跳出循环,因此理论上MLIGT算法的降相关效率要高于SEQR算法,并且随着模糊度维数的升高,这种差距还会进一步增大。
此外,相较于LIGT算法和SEQR算法,MLIGT算法在求解模糊度的过程中解算时间表现得更为稳定。
3 结语在高维模糊度解算过程中,提高降相关效率是提高整体解算效率中最为关键的问题。本文在LIGT算法基础上分别从减少条件方差交换次数和减少整数高斯变换次数2个方面进行改进,从而提高了算法的降相关效率,并通过模拟实验和实测实验共同验证了MLIGT算法的有效性。实测数据实验结果表明,MLIGT算法具有更少的降相关时间和整体解算时间,即MLIGT算法的降相关效率更高;此外,通过2组各1 000历元的实测数据实验计算出,MLIGT算法具有更小的总体时间标准差,因此在总体解算时间上MLIGT算法具有更好的稳定性。
| [1] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82 DOI:10.1007/BF00863419
(  0) 0) |
| [2] |
程建华, 王晶, 晏亮, 等. 高维情况下双差整周模糊度LAMBDA法解算分析[J]. 哈尔滨工程大学学报, 2012, 33(4): 470-475 (Cheng Jianhua, Wang Jing, Yan Liang, et al. Analysis of a Double-Differ Ambiguity Solution by the LAMBDA Method in High Dimensional Application[J]. Journal of Harbin Engineering University, 2012, 33(4): 470-475 DOI:10.3969/j.issn.1006-7043.201105022)
(  0) 0) |
| [3] |
Chang X W, Yang X, Zhou T. MLAMBDA: A Modified LAMBDA Method for Integer Least-Squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565 DOI:10.1007/s00190-005-0004-x
(  0) 0) |
| [4] |
Xu P L. Parallel Cholesky-Based Reduction for the Weighted Integer Least Squares Problem[J]. Journal of Geodesy, 2012, 86(1): 35-52 DOI:10.1007/s00190-011-0490-y
(  0) 0) |
| [5] |
卢立果, 鲁铁定, 吴汤婷, 等. 下三角Cholesky分解的整数高斯变换算法[J]. 测绘科学, 2017, 42(12): 57-62 (Lu Liguo, Lu Tieding, Wu Tangting, et al. Integer Gauss Transformation Algorithm Based on Low Triangular Cholesky Decomposition[J]. Science of Surveying and Mapping, 2017, 42(12): 57-62)
(  0) 0) |
| [6] |
Hassibi A, Boyd S. Integer Parameter Estimation in Linear Models with Applications to GPS[J]. IEEE Transactions on Signal Processing, 1998, 46(11): 2 938-2 952 DOI:10.1109/78.726808
(  0) 0) |
| [7] |
Lenstra A K, Lenstra Jr H W, Lovász L. Factoring Polynomials with Rational coefficients[J]. Mathematische Annalen, 1982, 261(4): 515-534 DOI:10.1007/BF01457454
(  0) 0) |
| [8] |
Ling C, Howgrave-Graham N. Effective LLL Reduction for Lattice Decoding[C]. 2007 IEEE International Symposium on Information Theory, Nice, 2007
(  0) 0) |
| [9] |
Xie X H, Chang X W, Borno M A. Partial LLL Reduction[C]. IEEE GLOBECOM 2011, Houston, 2011
(  0) 0) |
| [10] |
Nguên P Q, Stehlé D. Floating-Point LLL Revisited[C]. Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, 2005
(  0) 0) |
| [11] |
Fontein F, Schneider M, Wagner U. PotLLL: A Polynomial Time Version of LLL with Deep Insertions[J]. Designs, Codes and Cryptography, 2014, 73(2): 355-368 DOI:10.1007/s10623-014-9918-8
(  0) 0) |
| [12] |
Xu P L. Random Simulation and GPS Decorrelation[J]. Journal of Geodesy, 2001, 75(7-8): 408-423 DOI:10.1007/s001900100192
(  0) 0) |
2. Fuzhou Investigation and Surveying Institute, 1 Gaoxin Road, Fuzhou 350108, China;
3. School of Surveying and Urban Spatial Information, Henan University of Urban Construction, Longxiang Road, Pingdingshan 467036, China
 2021, Vol. 41
2021, Vol. 41


