2. 地理国情监测技术应用国家地方联合工程研究中心, 兰州市安宁西路118号, 730070;
3. 甘肃省地理国情监测工程实验室, 兰州市安宁西路118号, 730070
大气扰动会对地壳形变和地面重力产生周期性的影响,并且是cm级的反馈,在高精度大地测量研究中无法忽略[1-2]。计算大气负荷对地壳影响的方法主要是基于Longman地球负荷理论、负荷格林函数、球谐函数、大气导纳[3-4]等,采用的数据为全球大气模型数据或区域气象站气压数据[5]。
本文收集了2012~2017年兰新铁路线周边包括甘肃、宁夏、青海各省部分区域的全球大气数据和气象站数据,采用移去-恢复法分析该区域在6 a间大气负荷对地壳形变和地面重力的影响及整体变化规律。
1 基本理论 1.1 地壳负荷形变理论根据弹性地球负荷响应理论,将区域大气模型和全球大气模型转换为区域和全球等效水高,本文研究的等效水高变化量为某一时刻等效水高值与参考基准时刻等效水高之差,或相对于某一时间段等效水高平均值之差。地壳负荷形变理论及其具体计算公式可以参考文献[6]。
1.2 移去-恢复法理论大地高精确转化为正常高的方法有几何拟合法和移去-恢复法两种。几何拟合法适用于大地水准面变化均匀而缓慢的平坦地区,而在山区和丘陵地区,由于地势起伏较大,单纯的几何拟合法无法满足其精度要求,因此需引入移去-恢复法来提高计算精度,减小单独使用全球模型计算时的误差,更准确地表现出大气负荷对区域影响的变化特征[7],其主要计算流程见图 1。

|
图 1 计算流程 Fig. 1 Calculation process |
研究区域为102°~107°E、34°~38°N范围内的兰新铁路线周边区域,包含2012-01~2017-12的数据。
2.2 区域形变数据采集与预处理 2.2.1 全球大气数据本文所需的全球大气数据来自欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts)的全球大气压变化的格网化模型[8]。将2011年10~12月的月均值气压数据作为基准扣除,并且按照1 hPa=10.2 mm的等效水高换算关系,将全球大气数据转化为等效水高进行表示。
2.2.2 区域气压数据区域气压数据来自中国气象数据网,共54个气象站数据。提取得到的气压数据点值需经过平面插值来实现网格化,本文选择了计算相对灵巧、适用范围较广的克里金插值法将气压数据内插为区域大气压变化格网数据。
3 大气负荷形变场的计算与分析分析数据发现,大气负荷对地壳形变的影响大体呈现出年周期性和季节性变化,每年的变化趋势随着季节的变化而产生近似的形变量以及移动方向。故本文选取2017年3月、6月、9月、12月的数据分别对地壳垂直及水平形变、垂线偏差和地面重力影响进行研究。
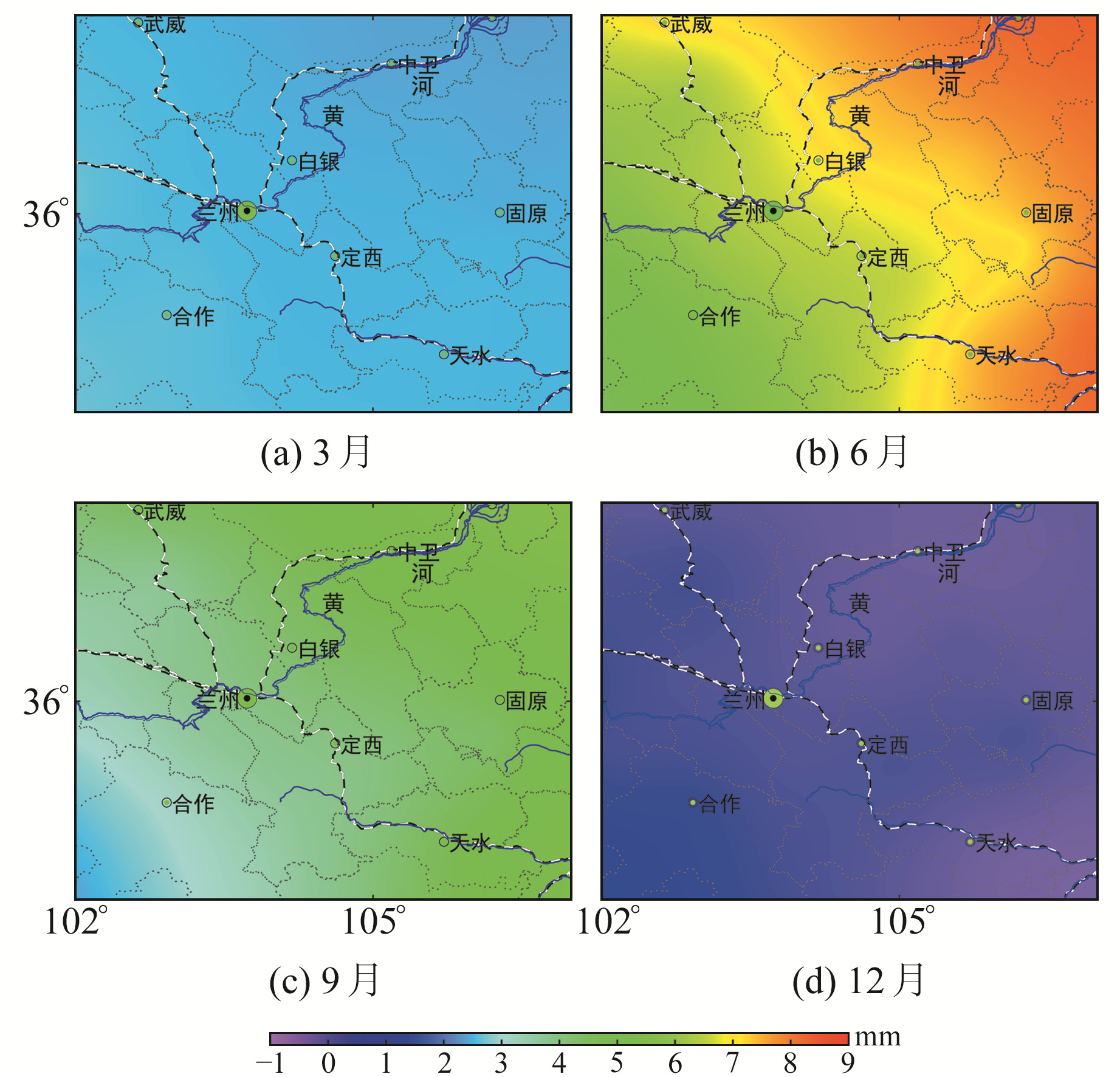
3.1 大气负荷对地壳形变的影响 3.1.1 大气负荷对垂直形变的影响根据负荷形变理论,将2011年10~12月的月均值气压数据基准扣除,再运用移去-恢复法将区域大气等效水高转化为区域高精度大气负荷影响值。图 2为2017年4个月份的垂直形变,由图可见,3月形变量在3 mm左右;12月垂直形变量在-1~1 mm之间,为一年中最小,在甘肃省、宁夏境内形变量为1 mm左右;6月的垂直形变量最大,并且线路北部形变量整体略高于南部,最大处出现在宁夏中卫附近,年变化幅度大约为10 mm。
|
图 2 2017年大气负荷对地壳垂直形变的影响 Fig. 2 Vertical deformation caused by pressure loading in 2017 |
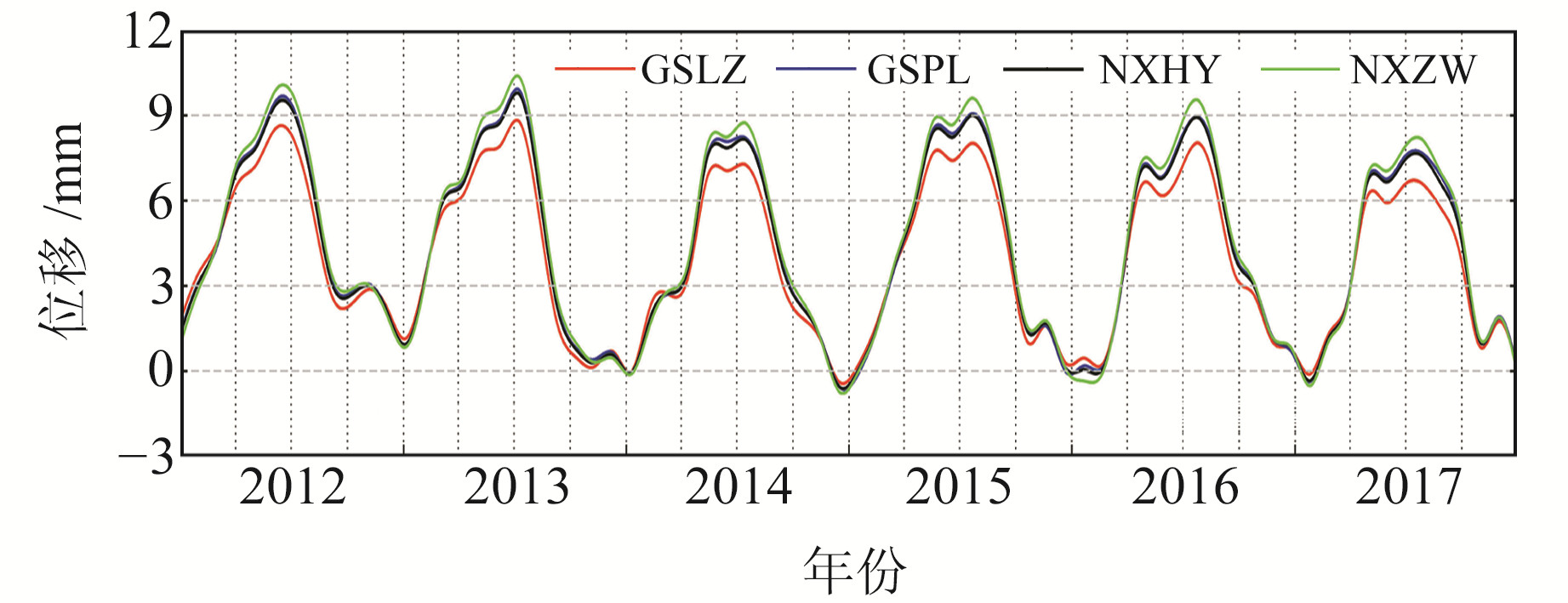
为了更好地研究其变化规律,选择区域内2012~2017年兰州(GSLZ)、平凉(GSPL)、海源(NXHY)、中卫(NXZW)4个连续运行参考站(CORS)的时间序列作为参考(图 3)。可以看出,4个地区的CORS站点每年的形变趋势都呈现近似的年周期性和季节性特征,并且在每年的夏季变化量最大,达到9 mm,冬季形变量趋近于0 mm。大气负荷对地壳的垂直形变的影响表现为年周期性和季节性。
|
图 3 站点大气负荷对垂直形变影响时序对比 Fig. 3 Comparison of stationary atmospheric load to vertical deformation time series |
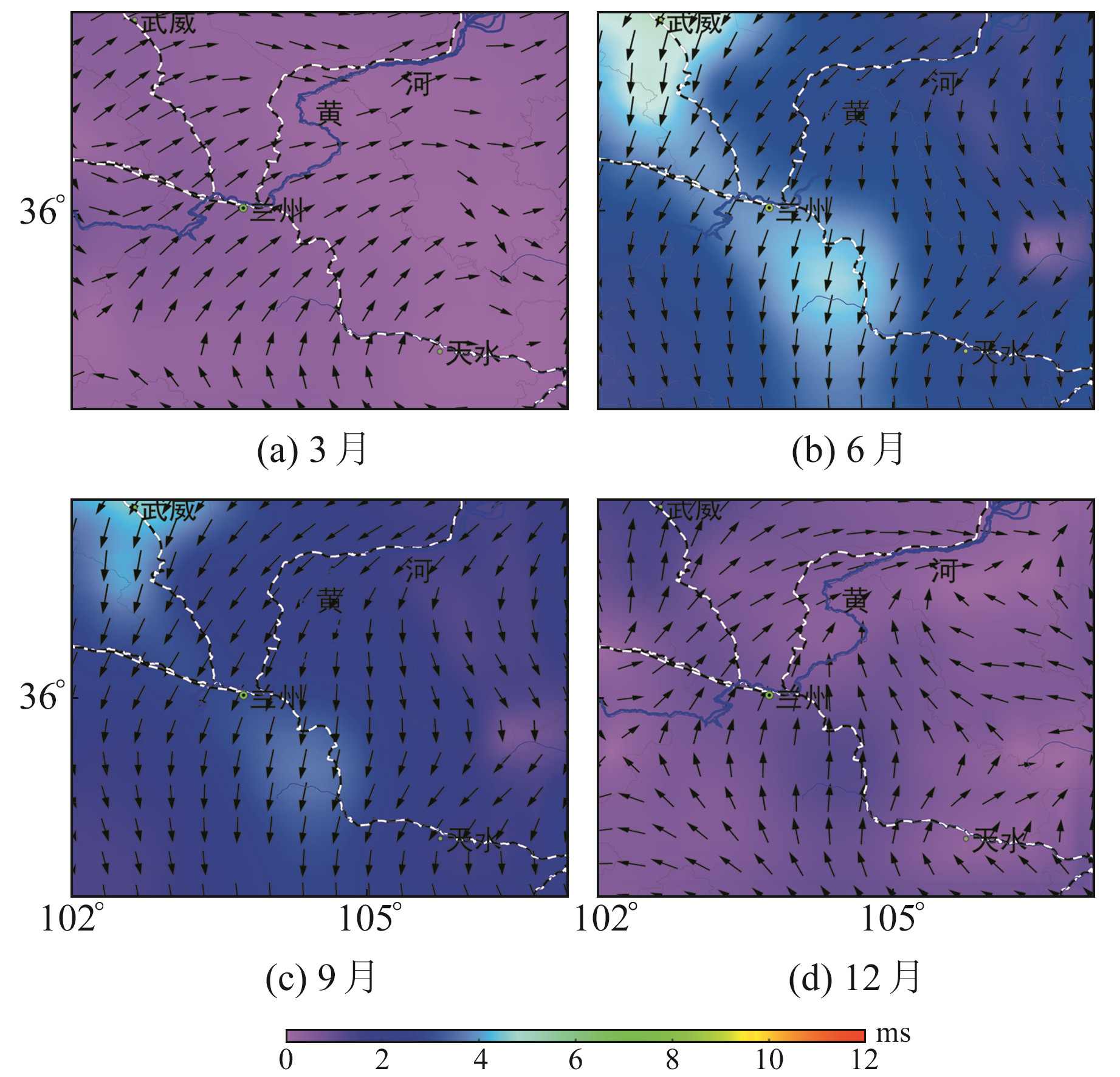
地壳水平形变、垂线偏差分为NS和EW两个分量,通过Python软件计算出两个分量平面向量的模,并绘制出平面速度场图和垂线偏差形变图。图 4为大气负荷对地壳水平形变的影响,由图可知,3月、12月的形变量接近0 mm, 6月、9月的变化量大致为1.1 mm。在兰新线沿线的武威、兰州、天水等区域年变化量趋于最大,为1 mm左右,比垂直形变变化量要小。图 5为大气负荷对垂线偏差的影响,由图可知,3月、12月的形变量大致为0 ms,6月、9月的形变值为6 ms左右,其变化量最大处也为兰新线沿线区域,为6 ms左右。总体而言,大气负荷对地壳水平形变、垂线偏差的影响也呈现出年周期性和季节性特征。

|
图 4 2017年大气负荷对地壳水平形变的影响 Fig. 4 Horizontal deformation caused by pressure loading in 2017 |
|
图 5 2017年大气负荷对地壳垂线偏差形变的影响 Fig. 5 Variation of vertical deviation caused atmospheric load in 2017 |
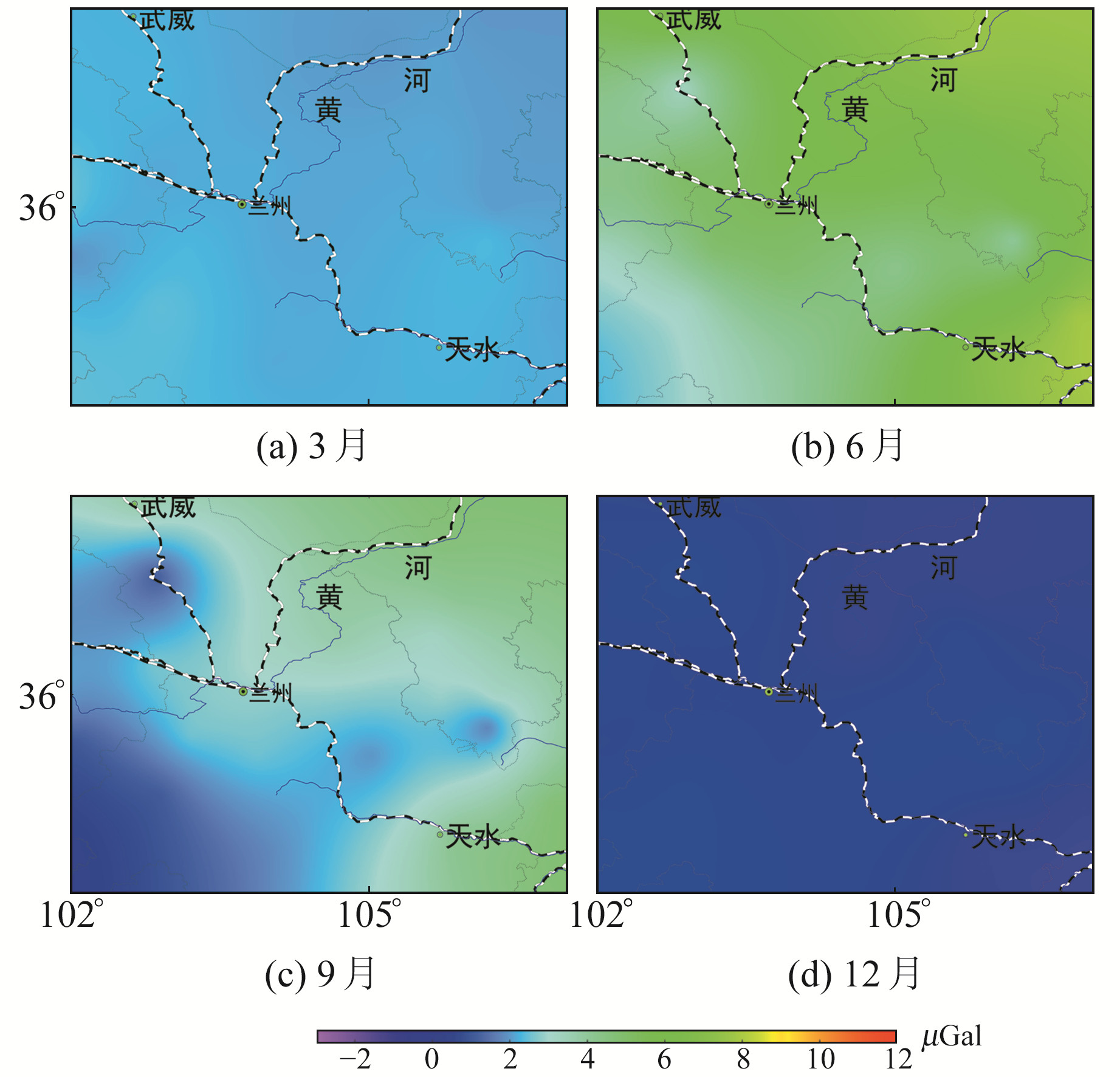
地面重力变化的影响因素分为直接影响和间接影响,其中直接影响占主要部分[9]。直接影响为大气压力对地面的直接作用,通过大气导纳的方法计算;间接影响为大气负荷变化对地球内部密度质量重新分布引起的重力变化,通过移去-恢复法进行计算。如图 6所示,6月的重力变化为一年中最大,趋近于7 μGal,12月的重力变化量为-2 μGal左右,年变化幅度大约为9 μGal。以兰新铁路为界线,线路以北区域重力变化量比线路以南区域要大,并且在6月、9月变化程度更加明显。由图可见,重力变化与大气压变化呈反比关系,即气压越大地面重力越小。
|
图 6 大气负荷对地面重力的影响 Fig. 6 Gravity change caused by atmospheric pressure loading |
为了更加具体地反映出大气负荷对兰新线区域大气负荷形变场和重力场的影响,本文对大气负荷月平均值、标准差和年变化幅度进行更近一步的统计(表 1)。由表 1看出,大气负荷对地壳形变和地面重力的影响具有年周期变化特征,一年中大气负荷对地壳在垂直方向的扰动幅度达到cm级,最大、最小值分别为7.10 mm、0.00 mm,其变化幅度在4种影响类型中最大,为8.35 mm;对地面重力的影响最大值为5.04 μGal,最小值为0.00 μGal;在水平方向影响最小,不超过2 mm;大气负荷对垂线偏差影响较大,达到6.74 ms。
|
|
表 1 大气负荷对大地测量要素影响统计 Tab. 1 Influence statistics of atmospheric load on geodetic factors |
本文选取2012~2017年兰新铁路线周边区域的全球大气模型数据和区域气象站数据,基于大气负荷理论,采用移去-恢复法计算出该区域在6 a间的高精度大气负荷影响值,得到大气负荷对兰新线周边区域地壳形变和地面重力的影响。结果表明,大气负荷引起的地壳及地面的重力变化表现出季节性和年周期性特征,对该区域在垂直方向的影响达到cm级,接近1 cm;水平方向的变化量不足2 mm,较其他影响要素而言变化较小;对垂线偏差影响的年变化量大致为6 ms,并且在甘肃区域的线路周边变化幅度更加明显;对地面重力的影响幅度达到了6 μGal。本文成果可为研究兰新线区域大气负荷对地壳形变及重力变化的影响、局部区域地壳形变规律提供参考。
| [1] |
罗少聪, 孙和平, 徐建桥. 大气负荷引起的重力与位移变化理论计算的精度估计[J]. 测绘学报, 2001, 30(4): 309-315 (Luo Shaocong, Sun Heping, Xu Jianqiao. Theoretical Computation in the Precision Estimation of the Change in Gravity and Displacements Due to Atmospheric Loading[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 309-315 DOI:10.3321/j.issn:1001-1595.2001.04.007)
(  0) 0) |
| [2] |
黄勇. 大气负荷的理论研究[D]. 武汉: 武汉大学, 2003 (Huang Yong. Theoretical Research of Atmospheric Loading[D]. Wuhan: Wuhan University, 2003)
(  0) 0) |
| [3] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797 DOI:10.1029/RG010i003p00761
(  0) 0) |
| [4] |
Spratt R S. Modelling the Effect of Atmospheric Pressure Variations on Gravity[J]. Geophysical Journal of the Royal Astronomical Society, 2010, 71(1): 173-186
(  0) 0) |
| [5] |
王伟, 章传银, 杨强, 等. 大气负荷对区域地壳形变和重力变化的影响分析[J]. 武汉大学学报: 信息科学版, 2018, 43(9): 1 302-1 308 (Wang Wei, Zhang Chuanyin, Yang Qiang, et al. Impact of Atmospheric Pressure Loading on Regional Crustal Deformation and Gravity Change[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1 302-1 308)
(  0) 0) |
| [6] |
王伟, 党亚民, 章传银, 等. 基于CORS站网监测三峡地区陆地水负荷对地壳形变和重力变化的影响[J]. 地球物理学报, 2017, 60(3): 962-971 (Wang Wei, Dang Yamin, Zhang Chuanyin, et al. Monitoring of Crustal Deformation and Gravity Variation from Terrestrial Water Loading in the Three Gorges Region by the CORS Network[J]. Chinese Journal of Geophysics, 2017, 60(3): 962-971)
(  0) 0) |
| [7] |
李冲, 刘站科. 几种移去-恢复法的比较分析[J]. 测绘工程, 2009, 18(5): 41-43 (Li Chong, Liu Zhanke. Analysis and Comparison of Several Remove-Restore Model[J]. Engineering of Surveying and Mapping, 2009, 18(5): 41-43 DOI:10.3969/j.issn.1006-7949.2009.05.011)
(  0) 0) |
| [8] |
Ray R D, Ponte R M. Barometric Tides from ECMWF Operational Analyses[J]. Annales Geophysicae, 2003, 21(8): 1 897-1 910 DOI:10.5194/angeo-21-1897-2003
(  0) 0) |
| [9] |
王海涛, 王斌, 王伟, 等. 大气负荷对新疆地区地壳形变和地面重力变化的影响[J]. 大地测量与地球动力学, 2019, 39(2): 189-194 (Wang Haitao, Wang Bin, Wang Wei, et al. Research on the Effect of Atmospheric Pressure Load on Crust Deformation and Gravity Change in Xinjiang Region[J]. Journal of Geodesy and Geodynamics, 2019, 39(2): 189-194)
(  0) 0) |
2. National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, 118 West-Anning Road, Lanzhou 730070, China;
3. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, 118 West-Anning Road, Lanzhou 730070, China
 2021, Vol. 41
2021, Vol. 41

