2. 中国地震局地球物理研究所, 北京市民族大学南路5 号, 100081;
3. 湖北省地震局, 武汉市洪山侧路40 号, 430071
背景噪声是地震计在未发生地震时拾取的在地球内部传播的弹性波,包含地球内部的全部信息,可用于地壳结构成像、火山爆发监测等。关于地球背景噪声的研究主要集中在2个方面:1)地球噪声模型、噪声产生的机制和源。如Peterson[1]提出地球新噪声模型;Stehly等[2]通过求取噪声相关函数的包络,获得归一化的噪声背景能量流(normalized background energy flux, NBEF); Stutzmann等[3]分析全球气候对背景噪声的时间演化关系。2)地球背景噪声的利用。根据背景噪声的自互相提取格林函数进行地震成像研究[4]以及地震传感器其他性能研究,包括估算地震计自噪声[5]、地震计方位角偏差[6, 7]以及数据质量评估[8], 其中针对记录数据质量评估的研究主要集中在能量-频率分布特征方面。本文将采用分形新方法对地震传感器记录的数据进行质量评价。
1 地震背景噪声的分形性 1.1 时间序列分形属性如果时间序列x(t)具有自相似或自仿射等分形特征,则对于任何τ≥1, t1, t2, …tτ∈T和a > 0, x(t)应满足标度律:
| $\left[x\left(a t_{1}\right), x\left(a t_{2}\right), \cdots, x\left(a t_{\tau}\right)\right]= \\ \left[a^{n} x\left(t_{1}\right), a^{n} x\left(t_{2}\right) \cdots a^{n} x\left(t_{\tau}\right)\right], n>0$ | (1) |
式中,a为标度指数。由x(t)满足标度律可知,其功率谱密度S(f)满足负幂律:
| $S(f) \propto f^{-\beta}$ | (2) |
式中,β为功率谱密度指数。S(f)满足负幂律,且1 < β≤3为该时间序列分形的必要条件,即PSD法。
在实际数据处理中,实验对象不可能严格服从该规律,但在相当宽度的频带范围内满足标度律时可解释为分形[9]。
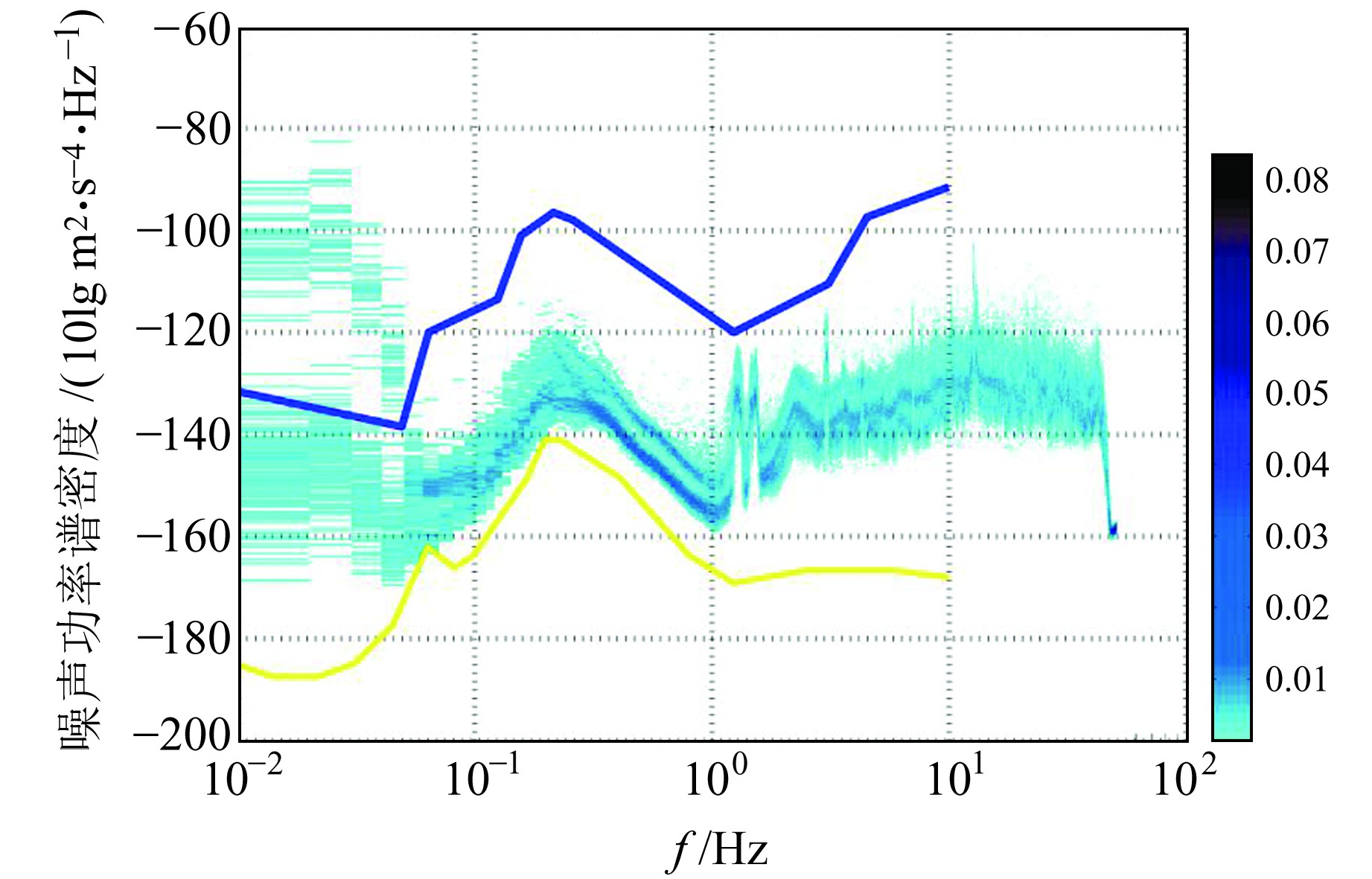
1.2 地球背景噪声分形性质通过对比Peterson[1]基于全球75个台站记录得到的新噪声模型(N噪声模型)、Khairy等[10]基于埃及国家地震台网7台宽频带地震计记录得到的E噪声模型以及El Fellah等[11]基于摩洛哥国家地震台网23台宽频带地震计记录得到的M噪声模型(图 1), 得出第二类地脉动中0.2~1 Hz频段内功率谱密度满足负幂律,因此推断该频段背景噪声具有分形性。基于该性质,下文将重点介绍该频带范围内背景噪声的分形分析与应用。
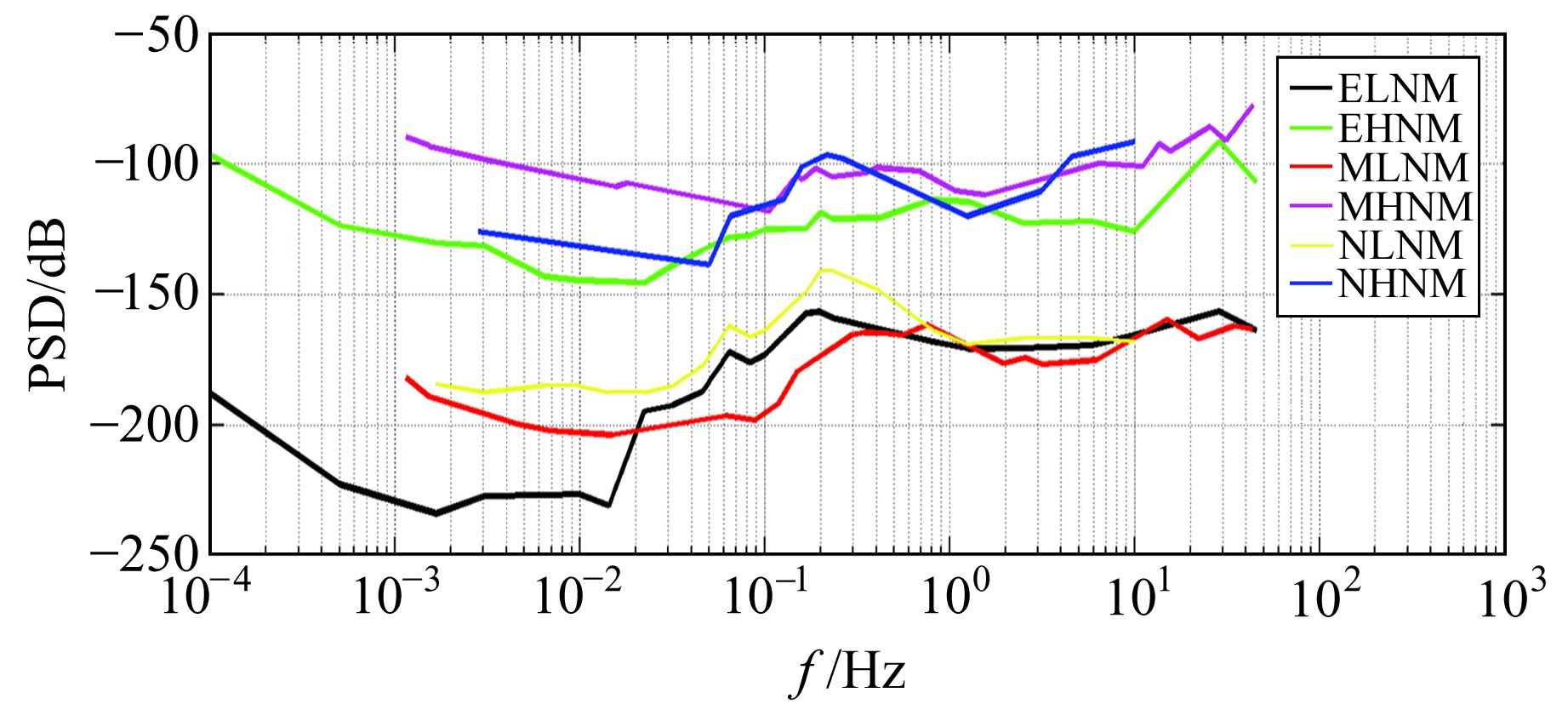
|
图 1 不同地球背景噪声模型对比 Fig. 1 Comparison of different Earth background noise models |
分形维数(fractal dimension)是分形理论中最核心的概念与内容[12]。其中,分形盒维数表明波形(图像)在一定标度下的不规则性或复杂性与波形频谱有关,也表示复杂性随标度减小而加剧的速率[13]。
对分形曲线y=f(x), 用尺度为δ的网格对其进行覆盖,所需网格数为Nδ, 则Nδ随δ的减小而增大,且满足:
| $N_{\delta}=k \delta^{-D}$ | (3) |
式中,D为曲线的分维数,也称为计盒维数,k为整数。
一维时间序列分形盒维数法采用已知宽度的栅格覆盖分形曲线(图 2), 栅格尺度(宽度)为δ。如第i个栅格内曲线段的计盒维数为:
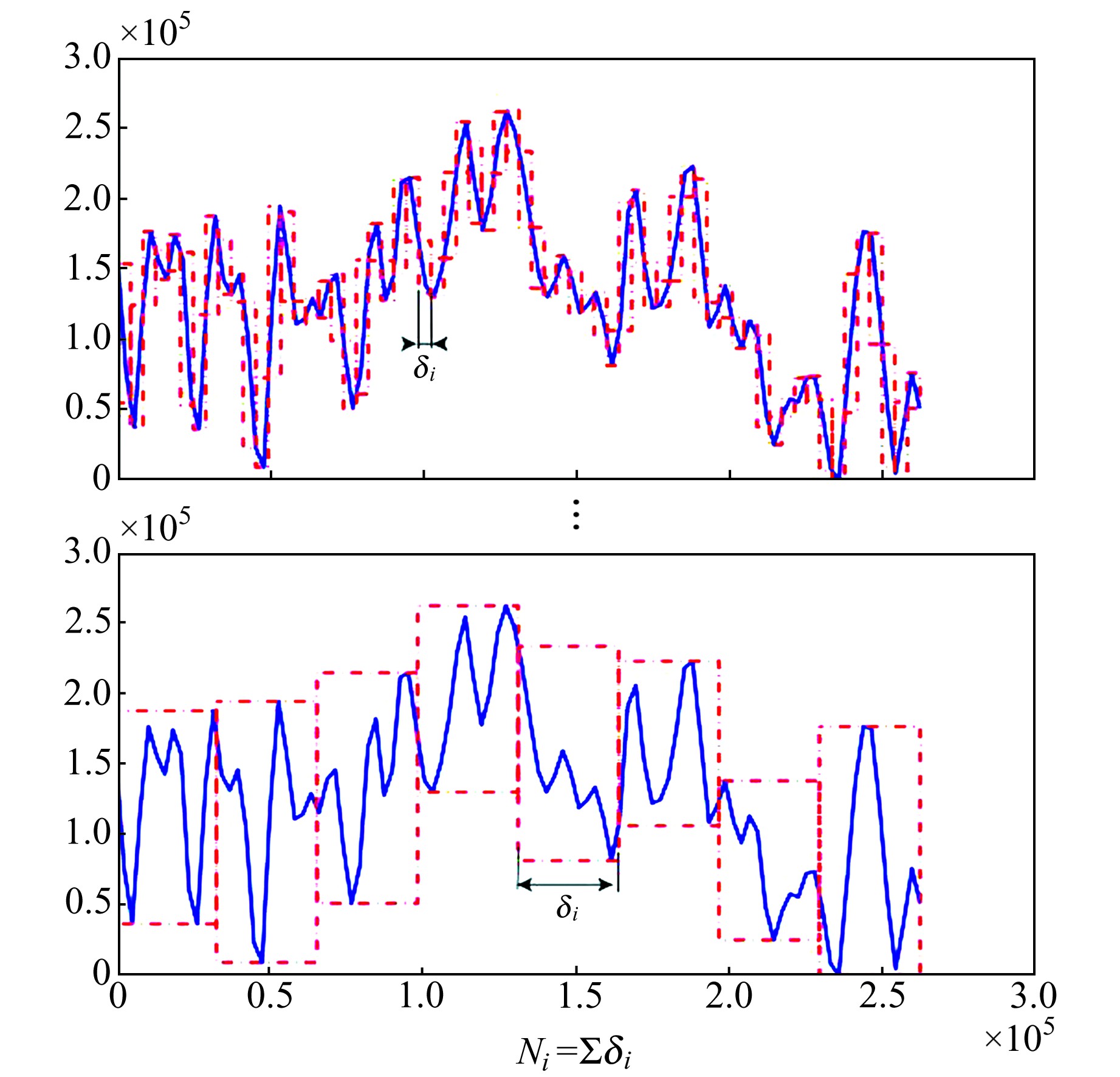
|
图 2 一维时间序列分形盒维数原理 Fig. 2 The diagram of fractal box dimension of one-dimensional time sequence |
| $N_{\delta}(i)=\frac{f_{\max }(i)-f_{\min }(i)}{\delta}$ | (4) |
则覆盖该曲线段的网格数
通过构造已知Hurst值的一维分形波形并进行多次比较验证,结果表明,上述算法能很好地反映理论盒维数的变化情况。
2.2 数据背景本文选取国家台网中心及广东省地震台网提供的23个在运行台站2015年的数据及中国地震局地球物理研究所提供的17个实验设备的记录数据进行分析,实验数据有效涵盖了我国台站运行环境。所选台站中,纬度最高的约53°N为漠河台(MOH), 最低的约16°N为西沙台(XSA), 实验范围跨越中国各个纬度带;在地域高程方面,都兰台(DUL)处于3 500 m以上的高寒地区。
表 1为本文使用的台站和地震计类型,包含我国在运行的4种主流地震计及17种国内外在运行或即将投入使用的地震计,可使实验结果具有一般性和普适性。
|
|
表 1 地震仪器分类及参数 Tab. 1 Classification and parameters of seismic instruments |
小波的自适应分解能力能有效地对背景噪声进行尺度(频段)划分,满足在一定尺度内对背景噪声进行自相似性分析的要求。根据本文所采用的地震仪的采样率(100 Hz), 选择哈尔小波为小波基进行8阶小波分解,提取子带6至子带8的数据(频带范围为0.2~1 Hz)进行盒维数估算。
图 3为不同尺度下盒维数分布图,子带6的盒维数集中在1.57~1.59之间,子带7的盒维数集中在1.49~1.50之间,子带8的盒维数集中在1.42~1.44之间,表明正常运行的宽频带地震计背景噪声在特定尺度下的分形盒维数稳定收敛。上述结果也表明,由于0.2~1 Hz为21种宽频带地震计(包括甚宽频带及超宽频段)的通频带,该尺度下分形盒维数与地震计种类及系统参数无关;同时,台站的地理位置和观测条件对实验结果影响较小。
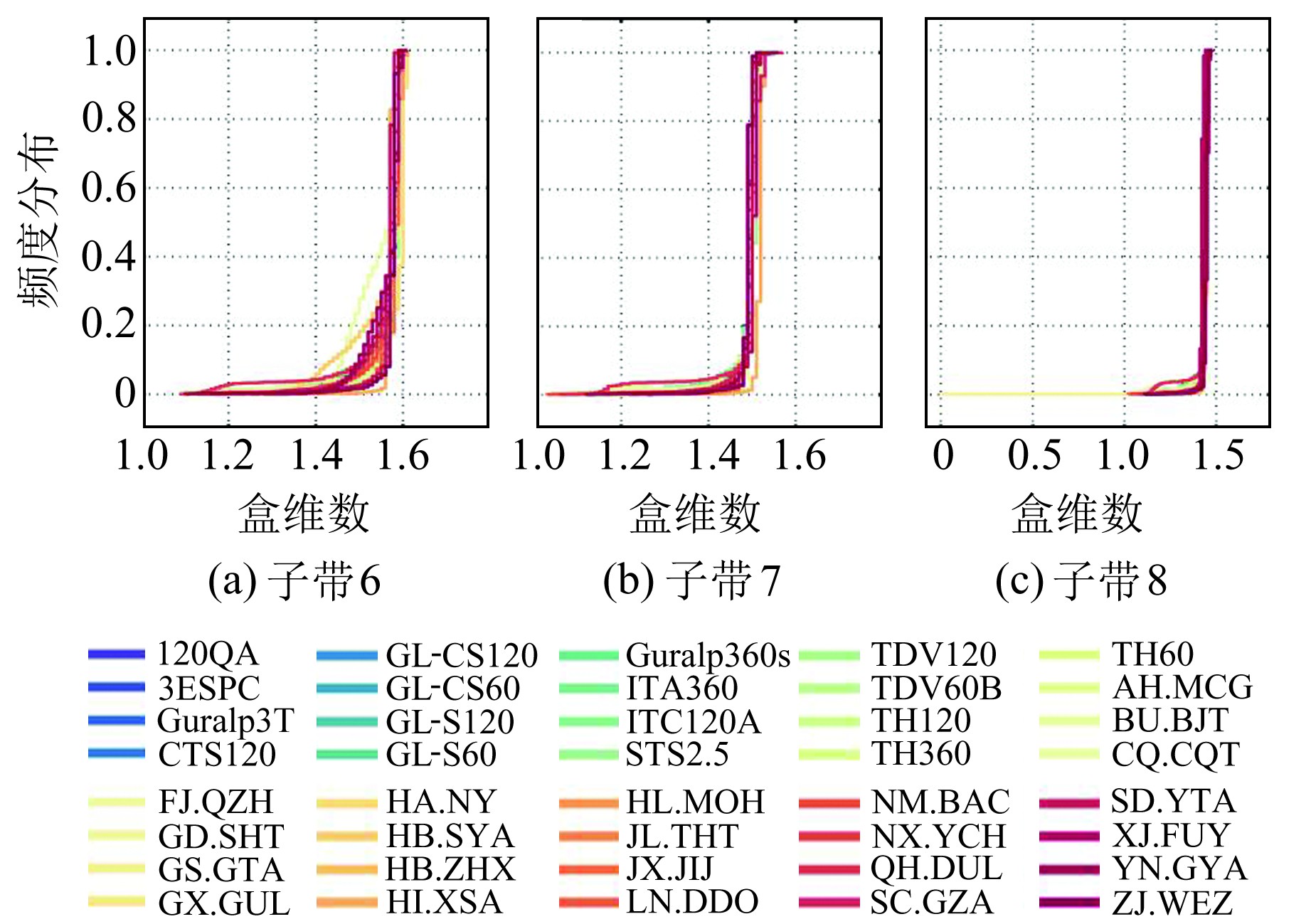
|
图 3 不同子带盒维数频度图 Fig. 3 Frequentness of box dimension of different subbands |
为进一步检验分形对仪器运行状态的监控能力,对部分已发生基本故障的地震计数据及部分地震事件进行分析。图 4为地震事件对实验结果的影响,图 4(a)为正常地脉动数据叠加近场干扰及地震事件的盒维数结果,其中紫色圈盒维数变化对应图 4(b)。从图 4(a)可以看出,近场地震事件的盒维数结果类似于近场干扰,盒维数变化与能量成反比,且与子带的频带范围有关,这种异常形态在背景噪声进行分形处理后较易识别。
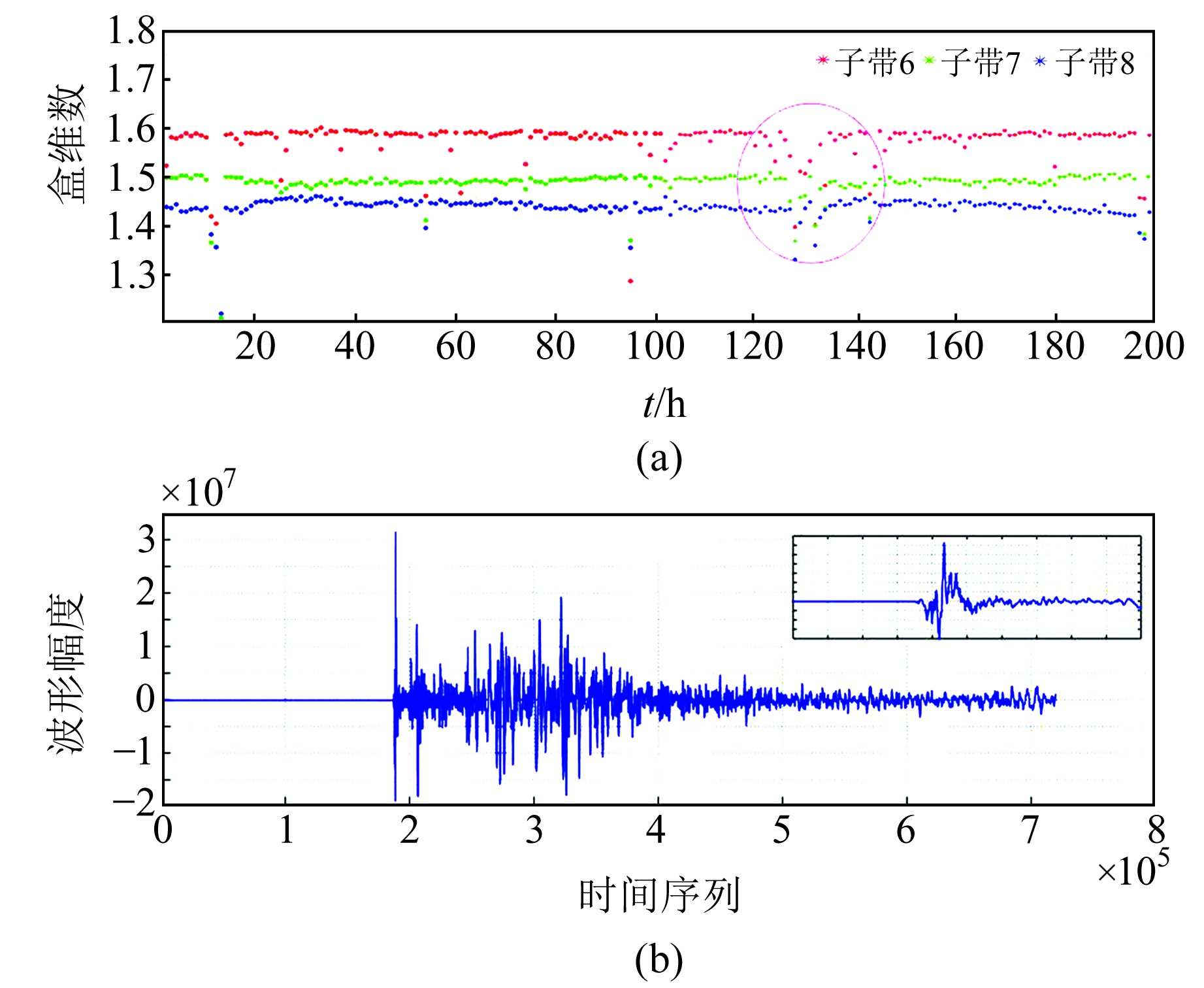
|
图 4 地震事件影响 Fig. 4 Influence of earthquake event |
图 5中地震仪处于不稳定工作状态,仪器异常时盒维数会出现明显突变。图 5(a)为正常地脉动数据叠加近场干扰及故障的盒维数结果,其中方框盒维数变化对应图 5(b)。图 5(b)为地震计零点漂移直至逐渐靠摆的过程,从图中可以看出,故障时段的盒维数与近场干扰存在差异,盒维数变化与子带的频带范围无关。近场干扰表现为盒维数变小的扰动,类似于图 5中近震事件;零漂至靠摆的盒维数表现为整体平行跳变。
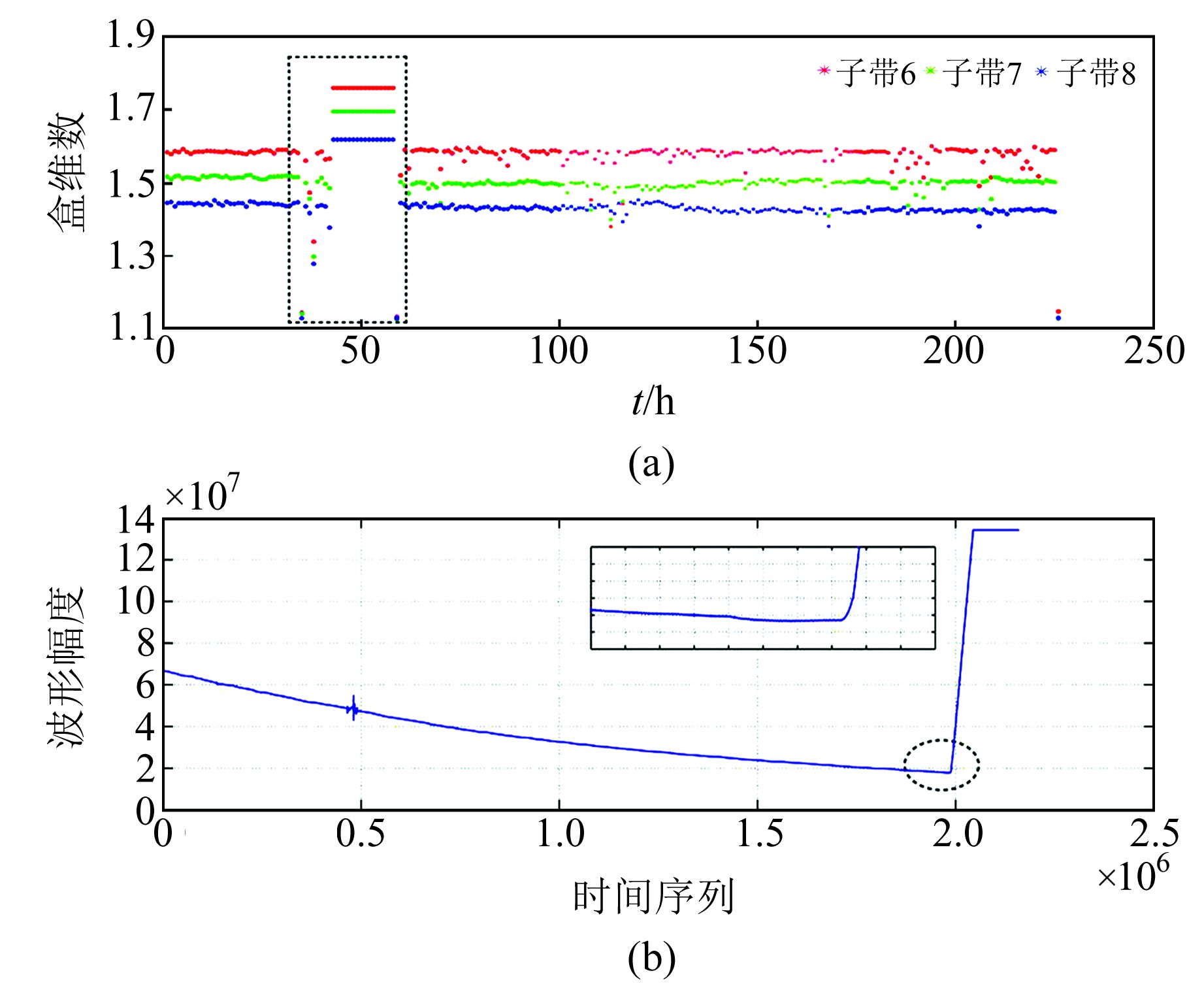
|
图 5 故障事件数据分析 Fig. 5 Data analysis of fault event |
结合盒维数结果与频域分析结果,根据采样定律可判断采集的数据头文件中采样率是否真实有效,当实际数据的采样率与本文默认采样率100 Hz不符合时,所计算的子带频域范围会因不满足标度律而不具有分形性。
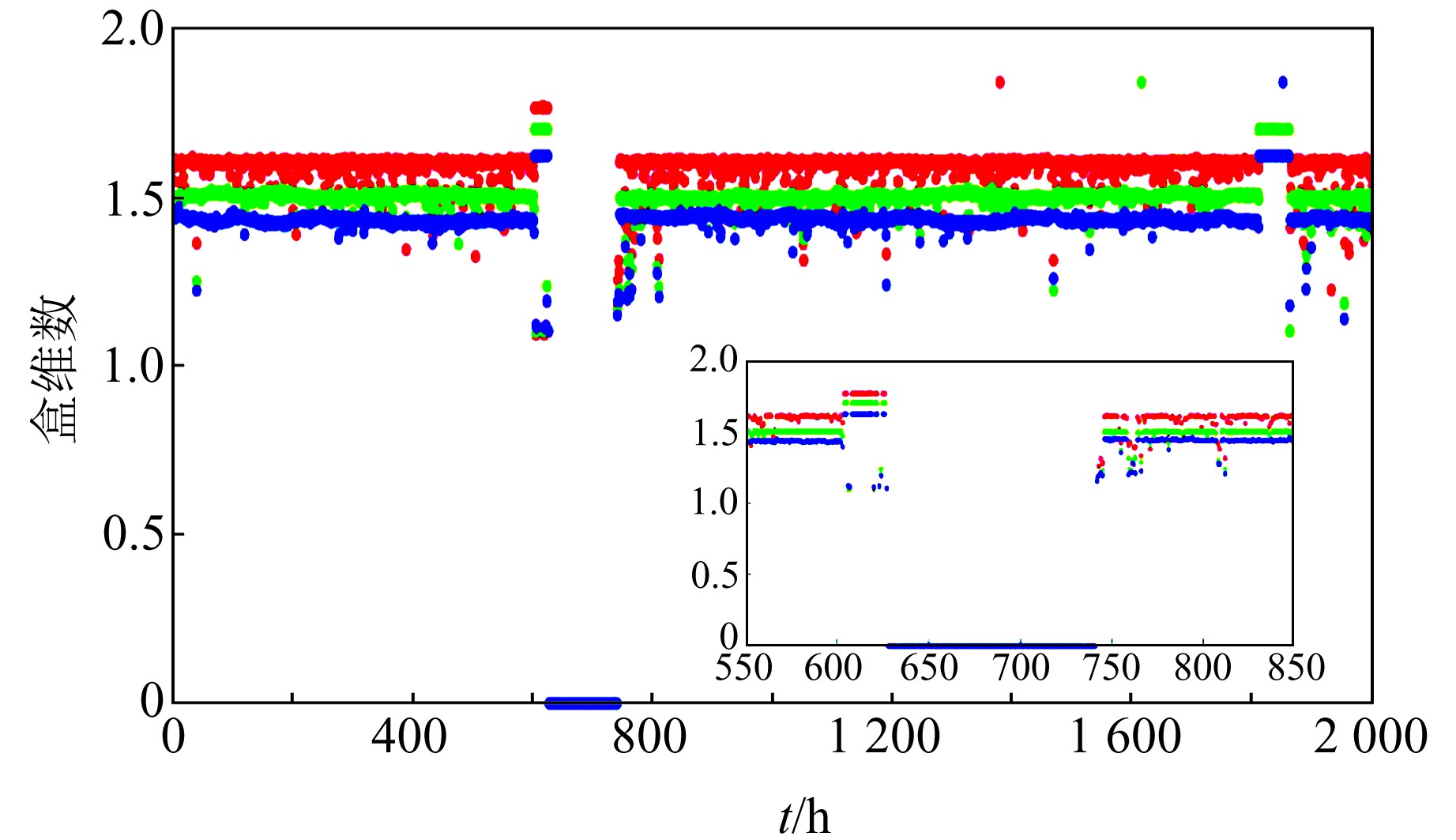
4 监控观测系统运行状态的可行性探讨利用噪声概率密度方法(图 6)和分形盒维数方法(图 7)对NY台3个月的数据进行处理。由噪声概率密度方法可知,该时间段内台基噪声频谱相对稳定,存在2个1.2~1.5 Hz频带的未知干扰,同时也存在少量异常记录。由图 7可知,台基噪声(0.2~1 Hz)波形在602 h(2015-10-26 07:00)零点漂移逐渐至靠摆;620 h(2015-10-27 01:00)地震观测系统无输出;745~749 h(2015-11-01 06:00~10:00)更换设备并进行电标定测试等,异常波形如图 8所示。
|
图 6 NY台噪声概率密度函数 Fig. 6 Probability density function of NY station |
|
图 7 NY台噪声分形盒维数 Fig. 7 Fractal box dimensions of NY station |
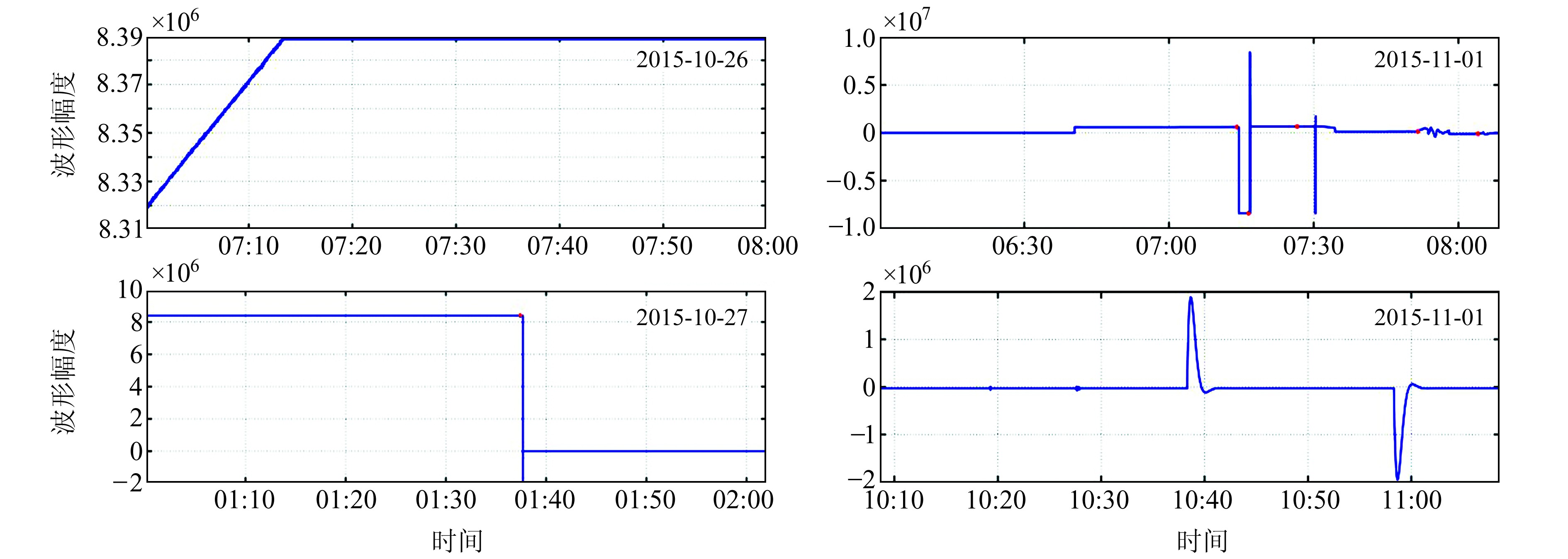
|
图 8 NY台异常波形 Fig. 8 Abnormal waveform of NY station |
与功率谱方法相比,分形盒维数方法可定量分析0.2~1 Hz频段范围内的异常波形,能准确定位到异常波形的时间。同时,该方法及结果与仪器参数无关,但该方法缺少全频带信息。可以看出,噪声功率谱方法及分形盒维数方法各有优缺点,通过噪声分析评价波形质量只能用来初步估计仪器的运行状态。
在测震台网产出维护中,现有的监测地震仪运行状态的方法主要是定期使用电流标定线圈激励法,根据标定数据计算结果来检查和验证地震计性能,包括阶跃标定、正弦标定以及伪随机码标定。与将噪声功率谱方法作为辅助分析类似,分形盒维数方法可通过对地震计背景噪声数据进行分形计算,获取盒维数并定量评价波形质量,进一步反映仪器工作状态,从而减少信息中断,远程监测地震计的运行状态。
5 结语利用地震计的日常记录评估地震计运行状态及数据质量,对提升台站观测系统运维能力具有实用意义。功率谱概率密度方法可分析频域范围内能量分布的相对变化,但无法在时间域内对地震仪器状态进行定量检测;而分形方法提出的时域波形复杂度研究可定量评估特定频段内波形状态。因此,相应标度下背景噪声的自相似性可与地震监测相结合,利用背景噪声在一定尺度下(频带范围内)的分形性质对地震观测仪器进行定量分析。在监控地震观测系统运行状态方面,该方法具有定量化程度高、抗干扰能力强、不受观测系统约束、可实现准实时化等优点。本文方法也可用于数据质量评价,同时实现非人为化操作并提高效率,进一步完善我国地震监测和预警系统的运维。
| [1] |
Peterson J. Observations and Modeling of Seismic Background Noise[J]. USGS Open File Report, 1993, 18(12): 93-322
(  0) 0) |
| [2] |
Stehly L, Campillo M, Shapiro N M. A Study of the Seismic Noise from Its Long-Range Correlation Properties[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B10)
(  0) 0) |
| [3] |
Stutzmann E, Schimmel M, Patau G, et al. Global Climate Imprint on Seismic Noise[J]. Geochemistry Geophysics Geosystems, 2009, 10(11)
(  0) 0) |
| [4] |
Yao H J, Hilst R D, Hoop M V. Surface-Wave Array Tomography in SE Tibet from Ambient Seismic Noise and Two-Station Analysis—I. Phase Velocity Maps[J]. Geophysical Journal International, 2006, 166(2): 732-744 DOI:10.1111/j.1365-246X.2006.03028.x
(  0) 0) |
| [5] |
Sleeman R, Wettum A, Trampert J. Three-Channel Correlation Analysis: A New Technique to Measure Instrumental Noise of Digitizers and Seismic Sensors[J]. Bulletin of the Seismological Society of America, 2006, 96(1): 258-271 DOI:10.1785/0120050032
(  0) 0) |
| [6] |
吕永清, 蔡亚先, 程骏玲. 确定地震计安装方位的相干性分析法[J]. 大地测量与地球动力学, 2007, 27(4): 124-127 (Lü Yongqing, Cai Yaxian, Cheng Junling. Orientation for Seismometer with Coherence Analysing Method[J]. Journal of Geodesy and Geodynamics, 2007, 27(4): 124-127)
(  0) 0) |
| [7] |
Xie J B, Yang D K, Ding L S, et al. A Comparison of Azimuth, Misalignment, and Orthogonality Estimation Methods in Seismometer Testing[J]. Bulletin of the Seismological Society of America, 2018, 108(2): 1 004-1 017
(  0) 0) |
| [8] |
齐军伟, 周云耀, 吕永清, 等. WTSB-120井下地震计和CTS-1甚宽频带地震计对比观测分析[J]. 大地测量与地球动力学, 2016, 36(增2): 31-35 (Qi Junwei, Zhou Yunyao, Lü Yongqing, et al. Comparison Analysis of Waveform Observation between WTSB-120 Borehole Seismometers and CTS-1 VBB Seismometers[J]. Journal of Geodesy and Geodynamic, 2016, 36(S2): 31-35)
(  0) 0) |
| [9] |
曹茂森, 任青文, 王怀洪. 基于小波与分形理论的地震异常检测[J]. 地球物理学报, 2005, 48(3): 672-679 (Cao Maosen, Ren Qingwen, Wang Huaihong. A Method of Detecting Seismic Singularities Using Combined Wavelet with Fractal[J]. Chinese Journal of Geophysics, 2005, 48(3): 672-679 DOI:10.3321/j.issn:0001-5733.2005.03.027)
(  0) 0) |
| [10] |
Khairy A E, Soliman M S. New Seismic Noise Models Obtained Using Very Broadband Stations[J]. Pure and Applied Geophysics, 2013, 170(11): 1 849-1 857 DOI:10.1007/s00024-013-0640-7
(  0) 0) |
| [11] |
El Fellah Y, Khairy A E, Harnafi M, et al. New Comprehensive Standard Seismic Noise Models and 3D Seismic Noise Variation for Morocco Territory, North Africa, Obtained Using Seismic Broadband Stations[J]. Exploration Geophysics, 2016, 48(3): 272-283
(  0) 0) |
| [12] |
李倩倩, 李春, 杨阳. 自相似性和分形维数在风场分析中的应用[J]. 动力工程学报, 2016, 36(11): 914-919 (Li Qianqian, Li Chun, Yang Yang. Application of Wind Speed Self-Similarity and Fractal Dimension in Wind Field Analysis[J]. Journal of Chinese Society of Power Engineering, 2016, 36(11): 914-919 DOI:10.3969/j.issn.1674-7607.2016.11.010)
(  0) 0) |
| [13] |
刘文涛, 陈红, 蔡晓霞, 等. 信号特征对分形维数的影响[J]. 火力与指挥控制, 2014, 39(9): 69-71 (Liu Wentao, Chen Hong, Cai Xiaoxia, et al. Signal Characteristics to Influence of Fractal Dimension[J]. Fire Control and Command Control, 2014, 39(9): 69-71)
(  0) 0) |
| [14] |
李剑, 孙才新, 杜林, 等. 局部放电灰度图象分维数的研究[J]. 中国电机工程学报, 2002, 22(8): 123-127 (Li Jian, Sun Caixin, Du Lin, et al. Study on Fractal Dimension of PD Gray Intensity Image[J]. Proceedings of the Chinese Society for Electrical Engineering, 2002, 22(8): 123-127)
(  0) 0) |
2. Institute of Geophysics, CEA, 5 South-Minzudaxue Road, Beijing 100081, China;
3. Hubei Earthquake Agency, 40 Hongshance Road, Wuhan 430071, China
 2021, Vol. 41
2021, Vol. 41

