自板块构造学说提出以来,环太平洋地震带一直是地震学家和地质学家研究的重点地区。对环太平洋俯冲带的研究是认识板块构造运动的有力证据,而发生在俯冲带的地震则是认识板块构造运动及板块间应力场状态的最有效手段。地震的本质是板块运动跨地质断层的错动,从纯物理的角度来看,地震是一种非平衡系统的耗散,地震的发生是一个能量释放的过程。
日本海沟是太平洋板块向欧亚板块俯冲,同时受菲律宾板块和欧美板块共同作用的结果(图 1), 是全球地震活动非常频繁的区域之一。海沟俯冲带的发现是板块构造运动的有力证据。Wadati[1]研究发现,发生在大洋中的深源地震会形成按一定规律排列的地震区,在此研究基础上发现了著名的Wadati-Benioff带。宁杰远等[2]利用1965~1982年的地震数据资料分析日本至中国东北地区地震深度的分布,认为日本本州至中国东北Benioff带具有连续性,中国东北区域深震为日本海下Benioff带的一部分。
|
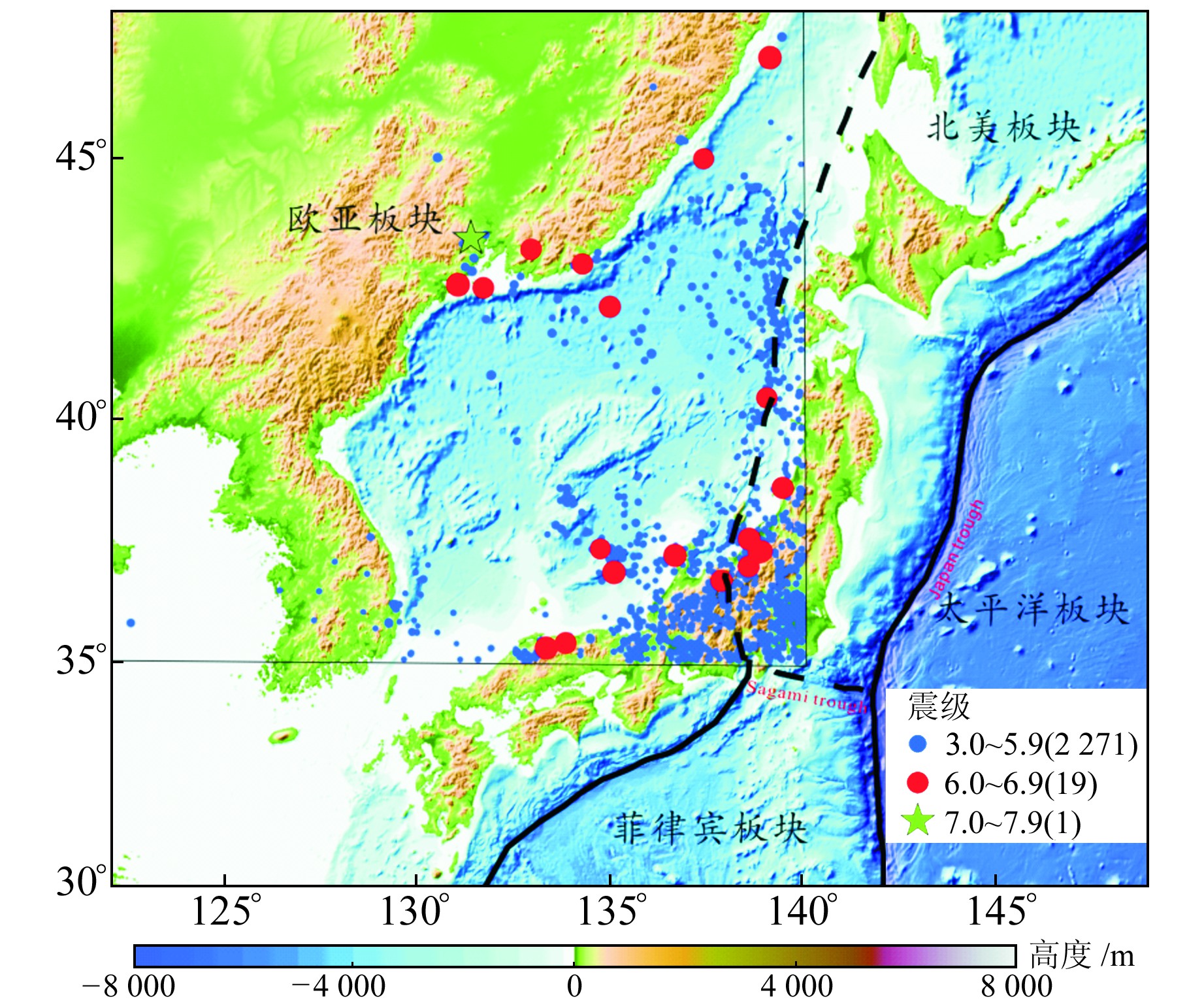
黑色实线为板块边界,黑色虚线表示正在逐渐成形的块体边界,蓝色、红色圆圈及绿色五角星为震中分布,矩形框为研究区 图 1 日本海沟至中国东北区域地形构造及研究区震中分布 Fig. 1 Topography structure and epicenters distribution of the study area from Japan trench to northeast China |
在日本3·11 MW9.0大地震发生以后,国内外许多学者对该区域的板块应力状态及同震效应进行了详细研究,并对日本海沟俯冲带区域的应力场变化进行分析,以期解释地震发生的相关物理过程。Yokota等[3]利用多种数据资料反演3·11大地震的破裂过程,结果显示,地震破裂长度为480 km, 宽度为180 km, 同震最大位移量达到35 m。陈为涛等[4]研究认为,该地震的同震位移在瞬间产生的形变量相当于中国东北地区12.7 a的长期应变积累。在俯冲带区域,主压应力轴在大震之前处于板块汇聚方向,大震之后地壳上盘及部分上隆区域出现张应力变化[5]。杨佳佳等[6]通过震源机制解反演日本3·11大地震震源区应力场变化发现,震源区主压应力轴和最大水平主压应力都发生了改变。
上述研究大多通过划分地震的区域和时间进行构造应力场分析,但关于Benioff带的空间三维构造应力场分析及与中国东北地区构造应力场的相关研究较少,因此难以从深度及空间方面分析该地区应力场变化的整体分布。为了更加科学和详细地认识日本海沟俯冲带的应力场变化及中国板块应力转换的过程,本文将基于震源机制解的数据资料进行空间应力场3D反演。通过分区域、分空间进行应力场反演,得到日本至中国东北地区的构造应力场及其空间变化,并以此为基础,探讨海沟俯冲带的具体分布情况,同时分析日本海沟俯冲带与中国东北Benioff带地下构造的相互作用,以期从更大范围认识板块运动的变化情况,为地震预测预报提供参考。
1 数据资料与研究方法 1.1 数据资料选取本研究收集了1997-01-01~2020-05-07 MW≥3.0共2 291个地震的震源机制解数据资料,所选数据纬度为35~50°N, 经度为122~140°E, 深度在0~700 km之间。所有数据资料均来源于NIED(National Research Institute for Earth Science and Disaster Prevention) F-net宽频带地震台网中心矩张量解目录。
1.2 研究方法应用震源机制解推断某一地区的应力场方向,是认识地壳运动和地震震源物理过程的有效方法之一。SATSI程序采用阻尼最小二乘法,可同时得到多个网格点的应力张量并进行平滑,具有良好的计算性能[7]。其基本原理为:最小化每一个断层面上的滑动矢量与剪应力的差别,建立断层面震源机制解参数与应力张量的线性关系:
| $\boldsymbol{Gm}=\boldsymbol{d}$ |
式中,矩阵G可由每个震源机制解的断层面滑动矢量得到,m为应力张量的单位模型矩阵向量,d为数据矩阵矢量。通过最小二乘法进行应力反演,其中应力张量的模型矩阵向量可确定最大主应力、中间主应力、最小主应力的方向及表示主应力相对大小的R值。本研究采用基于SATSI法发展而来的MSATSI构造应力反演方法[8], 可在MATLAB环境下进行完整的应力反演。由于本次研究基于3D反演进行区域应力场反演,每个网格点与周边6个网格点相邻,采用阻尼拟合参数会对每个网格点造成较大影响。应力场反演可得到反映应力相对大小的R值的量θ(θ=1-R=(σ2-σ3)/(σ1-σ3))和3个主应力的方位角与倾伏角,同时还可反演每个网格的极射赤平投影P、T轴分布图。R取不同值,相应的应力主轴表现结果会存在差异。R值可用来评估主应力轴方向的不确定性,取值范围为0~1。当R取值为0时,即主张应力轴方向确定,主压应力轴(σ1)取向与中间应力轴(σ2)取向趋于一致,并在垂直于主张应力轴(σ3)的平面内呈现挤压状态;当R取值为0.5时,表明主张应力轴与主压应力轴确定,相应的应力轴分辨状态趋于明显;当R取值为1时,表明主压应力轴方向确定,主张应力轴取向与中间应力轴取向趋于一致,并在垂直于主压应力轴的平面内旋转,同时呈现张性特征;R值在0~0.5时,中间应力轴的压性特征越来越明显;R值在0.5~1时,中间应力轴的张性特征越来越明显[6, 9-10]。
2 数据整理与分析 2.1 数据资料分区说明为从空间上给出日本至中国东北区域的构造应力场,以经度、纬度和深度为划分标准,对收集到的震源机制数据进行分区,将分区后的震源机制解数据置于3×4×5的矩阵网格中。将相应的网格矩阵单元作为固定区域的应力场反演区块,以序号为i、j、k的网格点对反演的区域进行命名分区。对于反演坐标轴中的X轴与Y轴,以5°×5°的经纬度进行区域划分。纬度在35°~40°划分为矩阵[i, 0, k]区(i、j、k表示对应矩阵网格的未知数),纬度在40°~45°划分为矩阵[i, 1, k]区,纬度在45°~50°划分为矩阵[i, 2, k]区。经度小于125°划分为矩阵[0, j, k]区,经度在125°~130°划分为矩阵[1, j, k]区,经度在130°~135°划分为矩阵[2, j, k]区,经度在135°~140°划分为矩阵[3, j, k]区。深度在0~30 km划分为矩阵[i, j, 5]区,深度在30~60 km划分为矩阵[i, j, 4]区,深度在60~100 km划分为矩阵[i, j, 3]区,深度在100~300 km划分为矩阵[i, j, 2]区,深度在300~500 km划分为矩阵[i, j, 1]区,深度在500~700 km划分为矩阵[i, j, 0]区,具体分区见表 1。虽然部分矩阵区块可能数据量小或缺少震源机制解数据资料,但不会对该区域整体应力场反演的过程及结果造成影响。根据矩阵分区规则,对各个存在震源机制解的网格区域进行统计及划分:矩阵[0,0,5]区分配到1个震源机制解;矩阵[1,0,5]区分配到28个震源机制解;矩阵[2,0,5]区分配到240个震源机制解;矩阵[3,0,5]区分配到1 083个震源机制解;矩阵[3,1,5]区分配到137个震源机制解;矩阵[3,2,5]区分配到2个震源机制解;矩阵[1,0,4]区分配到2个震源机制解;矩阵[3,0,4]区分配到276个震源机制解;矩阵[2,1,4]区分配到1个震源机制解;矩阵[3,1,4]区分配到1个震源机制解;矩阵[3,0,3]区分配到111个震源机制解;矩阵[3,0,2]区分配到169个震源机制解;矩阵[3,1,2]区分配到75个震源机制解;矩阵[2,0,1]区分配到30个震源机制解;矩阵[3,0,1]区分配到75个震源机制解;矩阵[2,1,1]区分配到7个震源机制解;矩阵[3,1,1]区分配到23个震源机制解;矩阵[3,2,1]区分配到3个震源机制解;矩阵[2,0,0]区分配到4个震源机制解;矩阵[2,1,0]区分配到20个震源机制解;矩阵[2,2,0]区分配到1个震源机制解;矩阵[3,2,0]区分配到2个震源机制解。为保证数据反演结果的可靠性,设置约束反演应力场的相关条件,见表 2。
|
|
表 1 矩阵网格划分标准 Tab. 1 Standard of matrix grid division |
|
|
表 2 应力反演的相关约束条件 Tab. 2 Relevant constraint condition for stress inversion |
在构造应力场研究中,由于地震发震的快速性特点,单个地震的P、T轴分布往往不能作为真实发震区域的应力场主轴分布方位。数值模拟分析表明,当地震发生的数量足够多时,大量震源机制解P、T轴的平均取向可代表该地区的主应力轴方位。图 2为本研究中相应区域的P、T轴平面分布图,用以可视化日本至中国东北震源机制解的分区情况及检验应力反演结果的可靠性[11-12]。

|
圆形网格表示赤平投影结果,其中红点表示P轴分布,蓝点表示T轴分布 图 2 震源机制解分区及各区P、T轴平面投影分布 Fig. 2 The distribution of focal mechanism solution and the plan projection of P axis and T axis of each region |
矩阵[1,0,5]区经度为125°~130°, 纬度为35°~40°, 深度为0~30 km, 本区反演共使用28个震源机制解,反演结果见图 2~3和表 3~4。反演结果表明,σ1轴的最优方位角为-11.20°, 角度变化范围为-21.70°~0.10°, 该区域主压应力轴为NNW向,与菲律宾板块挤压欧亚板块运动方向一致。倾伏角最优解为14.80°, 角度变化范围为-44.60°~26.40°, 倾伏角较小。σ2轴方位角为-124.00°, 为SSW向,倾伏角最优解为55.70°。σ3轴方位角最优解为87.60°, 角度变化范围为53.50°~248.40°, 为NEE-NE向,张应力轴近水平,角度变化范围较大,相应的最优解不确定度系数也较大。该区R值最优解为0.75, 表明该区压应力轴较稳定,中间应力轴与张应力轴性质趋于一致,反映该区压应力轴表现明显。
|
|
表 3 各分区构造应力反演结果 Tab. 3 Inversion results of tectonic stress in each subarea |
|
|
表 4 相关分区反演结果 Tab. 4 Inversion results of relevant subarea |
矩阵[2,0,5]区经度为130°~135°, 纬度为35°~40°, 深度为0~30 km, 本区共使用240个震源机制解进行反演,反演结果见图 2~3和表 3~4。反演结果表明,σ1轴方位角最优解为21.20°, 角度变化范围为17.00°~25.40°, 为NNE向,主压应力轴与矩阵[1,0,5]区相比存在明显偏转。σ3轴方位角最优解为118.00°, 角度变化范围为107.60°~116.00°, 为SEE向。主张应力轴和主压应力轴倾伏角近水平,R值最优解为0.45, 表明该区主压和主张应力轴均表现明显。
矩阵[3,0,5]区经度为135°~140°, 纬度为35°~40°, 深度为0~30 km, 该区反演共使用1 083个震源机制解,反演结果见图 2~3和表 3~4。反演结果表明,σ1轴最优方位角为25.30°, 角度变化范围为24.10°~28.50°, 主压应力轴仍为NNE向,表明在相同条件下,随着经度的增加,主压应力轴角度发生顺时针偏转。σ3轴方位角最优解为175.20°, 角度变化范围为133.40°~264.50°, 为SSE-SE向,而该处σ3轴倾伏角最优解为82.80°, 近于垂直。R值最优解为0.83, 表明主张应力轴水平向出现硬性阻碍物,导致倾伏角和R值变大。
矩阵[3,1,5]区经度为135°~140°, 纬度为40°~45°, 深度为0~30 km, 本区反演共使用137个震源机制解,反演结果见图 2~3和表 3~4。反演结果表明,σ1轴方位角最优解为6.90°, 角度变化范围为-1.60°~12.00°, 方位角为NNE-NE向,倾伏角最优解为6.20°, 显示出与[3,0,5]区相同的性质,倾伏角近水平。与[3,0,5]区的方位角相比,σ1轴随纬度的增加,主压应力轴趋于正NS向。σ3轴方位角最优解为-177.40°, 角度变化范围为-257.00°~-89.40°, 方位角为NNW向,倾伏角最优解为83.80°, 变化范围为62.70°~88.20°。R值最优解为0.76, 与同经度的[3,0,5]区相比,倾伏角表现结果一致,这进一步说明该区的应力场受某一区域块体控制。
2.2.2 深度30~60 km该深度仅矩阵[3,0,4]区满足相关反演要求,其经度为135°~140°, 纬度为35°~40°, 深度为30~60 km, 反演共使用276个震源机制解,反演结果见图 2~3和表 3~4。反演结果表明,σ1轴最优方位角为62.60°, 角度变化范围为56.90°~70.60°, 为NEE向,最优倾伏角较小,为23.30°。σ3轴方位角为171.70°, 角度变化范围为153.40°~218.00°, 方位角变化较大,为SSE-SE向;倾伏角最优解为37.10°, 变化范围为-1.30°~66.00°。R值最优解为0.87, 表明主压应力轴方向作用明显。
2.2.3 深度60~100 km该深度仅矩阵[3,0,3]区满足反演所需的震源机制解个数要求,其经度为135°~140°, 纬度为35°~40°, 深度为60~100 km, 该区反演共使用111个震源机制解,反演结果见图 2~3和表 3~4。反演结果显示,最大主压应力轴方位角为26.70°, 角度变化范围为-8.30°~44.80°, 为NNE-NE向,与相同经纬度、不同深度的[3,0,5]区和[3,0,4]区主压应力轴基本保持一致。最小主应力轴最优方位角为122.10°, 角度变化范围为88.00°~285.90°, 为SEE-SE向,角度变化范围较大。σ3轴最优倾伏角为55.80°, 角度变化范围为-29.50°~79.00°。与[3,0,5]区和[3,0,4]区相比,主张应力轴倾伏角逐渐变小。R值最优解为0.78, 表明该区仍被主压应力轴所控制。
2.2.4 深度100~300 km矩阵[3,0,2]区经度为135°~140°, 纬度为35°~40°, 深度为100~300 km, 该区反演共使用169个震源机制解,反演结果见图 2~3和表 3~4。反演结果表明,σ1轴最优方位角为-116.90°, 角度变化范围为-175.50°~48.30°, 为SWW-SW向,与矩阵[3,0,5]、[3,0,4]和[3,0,3]区相比,偏转角度逆时针陡增;σ1轴最优倾伏角为46.60°, 角度变化范围为-34.50°~87.40°, 与同经纬度的[3,0,5]、[3,0,4]和[3,0,3]区相比,倾伏角明显增大。σ3轴最优方位角为131.10°, 角度变化范围为78.90°~169.40°, 最大主张应力轴以SSE向为主,最优倾伏角为19.50°, 与同经纬度的[3,0,5]、[3,0,4]和[3,0,3]区相比,倾伏角明显变缓,说明到达该深度时障碍物的挤压作用明显下降。该区R值最优解为0.32, 表明该区主张应力作用较明显。
矩阵[3,1,2]区经度为135°~140°, 纬度为40°~45°, 深度为100~300 km。该区σ1轴最优方位角为-153.80°, 最大主压应力轴为SSW向,最优倾伏角为46.80°, 与同深度的[3,0,2]区基本一致,说明同深度主压应力轴横向压应力保持稳定状态。σ3轴最优方位角为-61.30°, 最大主张应力轴为NWW向,倾伏角最优解为2.30°, 与[3,0,2]区相比,角度偏转较大,向相反方向发生张性破裂。R值最优解为0.89, 表明该区以压性应力状态为主,与[3,0,2]区相反。
2.2.5 深度300~500 km矩阵[3,0,1]区经度为135°~140°, 纬度为35°~40°, 深度为300~500 km, 该区应力反演共使用75个震源机制解,反演结果见图 2~3和表 3~4。反演结果表明,σ1轴最优方位角为167.80°, 变化区间为162.00°~191.60°, 主压应力轴为SSE-SE向。与同经纬度、不同深度的[3,0,2]区存在明显差异,说明在该区约300 km处存在使主压应力轴发生偏转的巨大作用力。σ1轴最优倾伏角为37.40°, 倾伏角与[3,0,2]区相比明显变缓,进一步说明该区分界处存在巨大作用力。σ3轴最优方位角为54.40°, 变化范围为38.80°~77.60°, 最大主张应力轴为NEE向,倾伏角最优解为27.40°, 角度变化范围为5.80°~39.80°。该区张应力轴与同经纬度、不同深度的[3,0,2]区相比,NEE方向倾伏角变缓,表明阻碍张应力轴的障碍物逐渐减少。
矩阵[3,1,1]区经度为135°~140°, 纬度为40°~45°, 深度为300~500 km, 该区反演共使用23个震源机制解。反演应力结果表明,压应力轴与[3,0,1]区基本相同,说明该区的压应力轴较稳定,张应力轴与[3,0,1]区正好相反,说明该深度的2个区域的张性破裂受到2股应力影响。
矩阵[2,0,1]区经度为130°~135°, 纬度为35°~40°, 深度为300~500 km, 该区反演共使用30个震源机制解。反演结果显示,σ1轴与邻近矩阵区的轴方向呈现出一致的趋势性挤压,σ3轴也表现为趋势性拉张。
2.2.6 深度500~700 km该深度仅矩阵[2,1,0]区满足要求,经度为130°~135°, 纬度为40°~45°, 深度为500~700 km, 该区反演共使用20个震源机制解,反演结果见图 2~3和表 3~4。反演结果表明,σ1轴方位角最优解为173.20°, 角度变化范围为153.80°~210.20°, 倾伏角最优解为58.90°, 最大主压应力轴为SSE向。与300~500 km区域相比,方位角保持一定趋同性,倾伏角变大。σ3轴方位角最优解为-48.00°, 变化范围为-131.40°~56.90°, 倾伏角最优解为24.40°, 最大主张应力轴为NW向。与300~500 km区域相比,张应力轴向偏西方向偏转,倾伏角趋于平缓。
3 结语本文采用3D构造应力场反演,通过空间分区的方法,将收集到的2 291个震源机制解分配到相应区域中。分析结果表明:
1) 从日本东海岸到中国东北区域,构造应力场呈现明显的分层现象,地壳表层应力场与深源应力场具有明显差别,浅层构造应力场的主张和主压应力随经纬度的改变出现一定程度的旋转变化,各区的压应力轴受不同板块控制。岡田義光[13]研究认为,日本东北部属于北美板块,且日本东部边缘正在形成新的板块边界。由此可以看出,地壳浅层中各区主压应力与张应力不仅受到欧亚板块、菲律宾板块和太平洋板块的相互挤压碰撞,同时也受北美板块的斜插挤压作用,地壳应力结构复杂。矩阵[1,0,5]区的主压应力轴为NNW向,说明该区域的压应力主要来自于菲律宾板块,太平洋板块向西挤压为辅。[2,0,5]区与[3,0,5]区的主压应力轴为NNE向,与太平洋板块挤压欧亚板块的方向存在偏差,进一步说明该区处于板块交接处,受到北美板块强大的斜插作用。[3,1,5]区压应力轴方位角为6.90°, 与[2,0,5]区和[3,0,5]区相比,压应力轴呈近NS向,说明在经度相同的0~30 km深度,纬度越高,压应力轴受到的偏转作用力越强,北美板块的挤压斜插作用越剧烈。
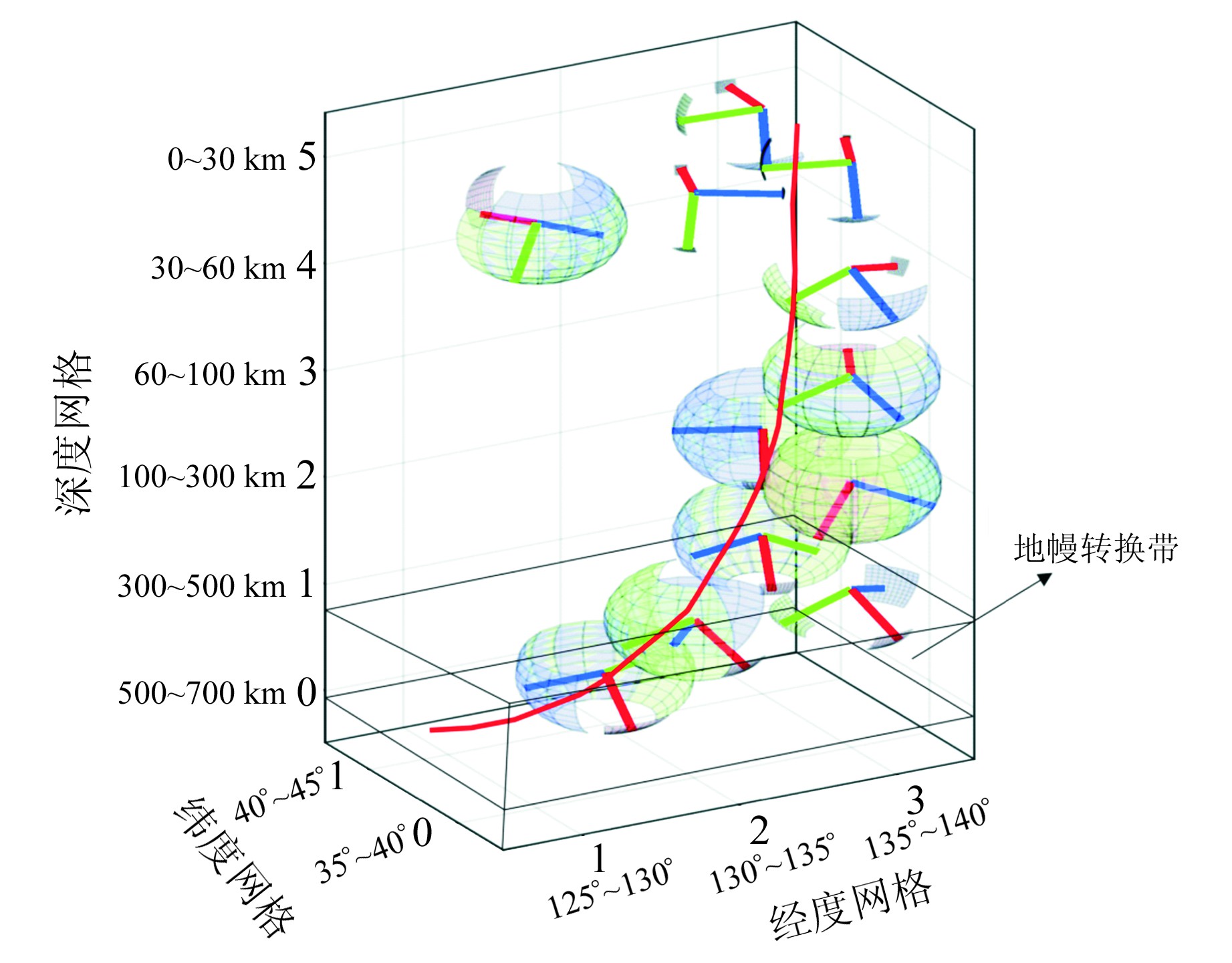
2) 由表 2和图 3可知,随着深度的增加,压应力轴及张应力轴在约300 km深处出现明显变化,最大主压应力轴由水平方向突然向下俯冲,随后俯冲速度以一定规律变缓,说明该区域在300 km以下已到达Benioff俯冲带,且俯冲带一直延伸到700 km左右。
|
纬度网格为Y轴,经度网格为X轴,深度网格为Z轴,红色柱棒为σ1轴,绿色棒柱为σ2轴,蓝色棒柱为σ3轴,红色线段为Benioff带走势曲线 图 3 各区网格矩阵构造应力场反演结果示意图 Fig. 3 Diagram of inversion results of tectonic stress field of grid matrix in each region |
3) 由表 2和图 3可以看出,最大主张应力轴在北美板块与欧亚板块的交接地带呈现出一定规律的俯冲现象,俯冲由浅部一直持续到300~500 km左右并逐渐变缓消亡。可以看出,随着时间的推移,北美板块在一定程度上继续向NE方向挤压欧亚板块,并持续发生地震。
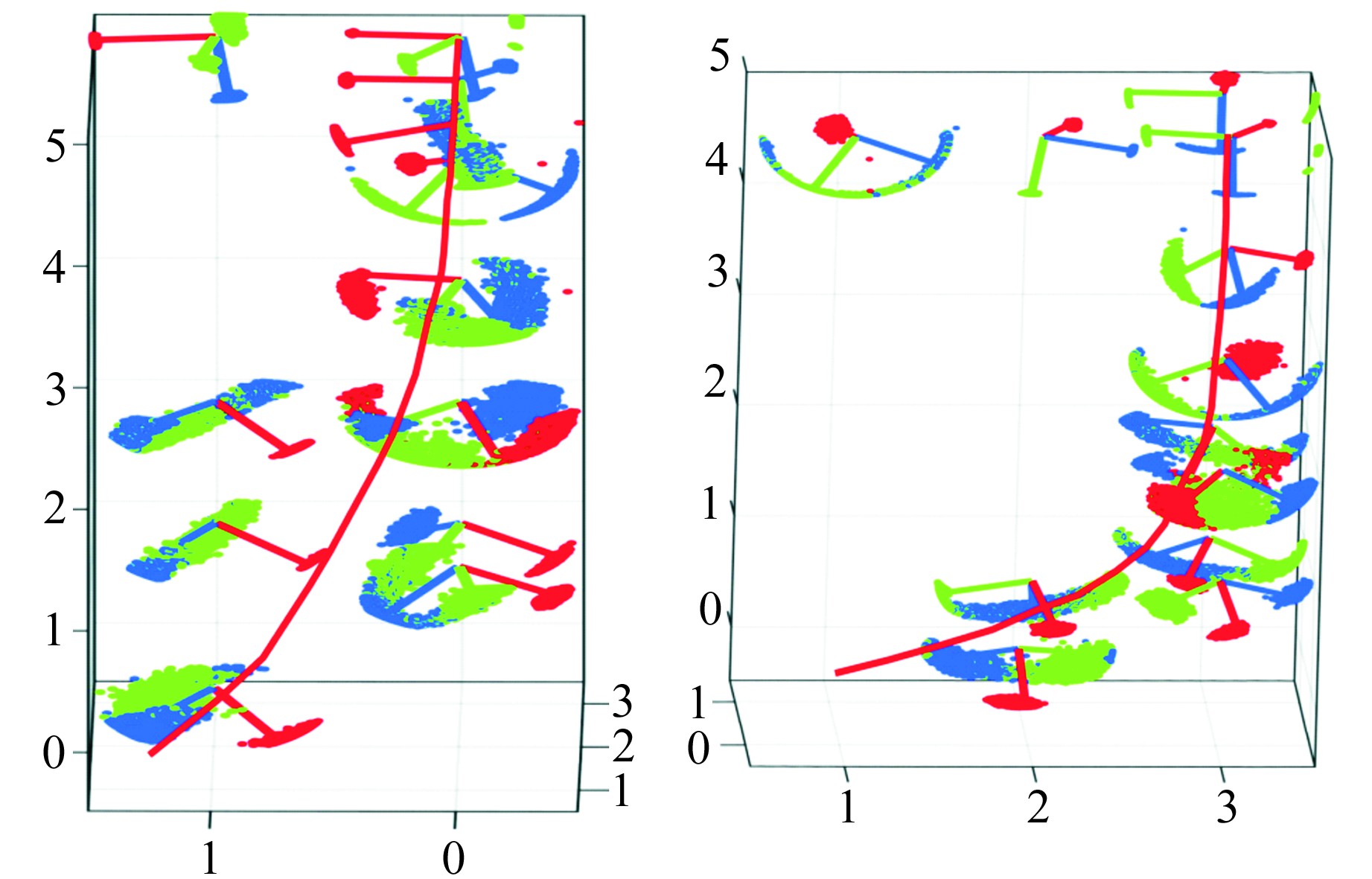
4) 由三维构造应力场图中主压应力轴可以看出,随着深度的增加,Benioff带向下凹陷俯冲。图 4为旋转后的三维立体图,从图中可以看出,俯冲过程一直延续到中国东北区域,该区域的深震与Benioff带的俯冲作用具有重要联系,Benioff带沿着日本海沟一线斜插入中国东北区域约500~700 km深处。
|
红色散点为σ1轴分布,绿色散点为σ2轴分布,蓝色散点为σ3轴分布,红色线段为Benioff带走势曲线 图 4 3D网格矩阵旋转后各区散点构造应力场反演结果示意图 Fig. 4 Diagram of inversion results of regional scattered tectonic stress field after 3D grid matrix rotation |
本次研究以空间三维的角度进行构造应力场反演,可更清晰有效地对某一地区的地块运动进行判断分析,但变化无处不在。本研究尚未涉及以时间轴为变化的空间四维应力场反演,后续将在该领域继续探索。
| [1] |
Wadati K. On the Activity of Deep-Focus Earthquakes in the Japan Islands and Neighbourhoods[J]. Geophysics, 1935, 8: 305-326
(  0) 0) |
| [2] |
宁杰远, 臧绍先. 日本海及中国东北地震的深度分布及其应力状态[J]. 地震地质, 1987, 9(2): 49-61 (Ning Jieyuan, Zang Shaoxian. The Distribution of Earthquakes and Stress State in the Japan Sea and the Northeast China[J]. Seismology and Geology, 1987, 9(2): 49-61)
(  0) 0) |
| [3] |
Yokota Y, Koketsu K, Fujii Y, et al. Joint Inversion of Strong Motion, Teleseismic, Geodetic, and Tsunami Datasets for the Rupture Process of the 2011 Tohoku Earthquake[J]. Geophysical Research Letters, 2011, 38(7)
(  0) 0) |
| [4] |
陈为涛, 甘卫军, 肖根如, 等. 3·11日本大地震对中国东北部地区地壳形变态势的影响[J]. 地震地质, 2012, 34(3): 425-439 (Chen Weitao, Gan Weijun, Xiao Genru, et al. The Impact of 2011 Tohoku-Oki Earthquake in Japan on Crustal Deformation of Northeastern Region in China[J]. Seismology and Geology, 2012, 34(3): 425-439 DOI:10.3969/j.issn.0253-4967.2012.03.004)
(  0) 0) |
| [5] |
Chiba K, Lio Y, Fukahata Y. Detailed Stress Fields in the Focal Region of the 2011 off the Pacific Coast of Tohoku Earthquake—Implication for the Distribution of Moment Release[J]. Earth, Planets and Space, 2012, 64(12): 1 157-1 165 DOI:10.5047/eps.2012.07.008
(  0) 0) |
| [6] |
杨佳佳, 张永庆, 谢富仁. 日本海沟俯冲带MW9.0地震震源区应力场演化分析[J]. 地球物理学报, 2018, 61(4): 1 307-1 324 (Yang Jiajia, Zhang Yongqing, Xie Furen. The Evolutionary Analysis of the Stress Field in the Seismic Focal Zone of the Great Tohoku-Oki Earthquake(MW=9.0)in the Japan Trench Subduction Zone[J]. Chinese Journal of Geophysics, 2018, 61(4): 1 307-1 324)
(  0) 0) |
| [7] |
Hardebeck J L, Michael A J. Damped Regional-Scale Stress Inversions: Methodology and Examples for Southern California and the Coalinga Aftershock Sequence[J]. Journal of Geophysical Research, 2006, 111(B11)
(  0) 0) |
| [8] |
Martínez-Garzón P, Kwiatek G, Ickrath M, et al. MSATSI: A MATLAB Package for Stress Inversion Combining Solid Classic Methodology, a New Simplified User-Handling, and a Visualization Tool[J]. Seismological Research Letters, 2014, 85(4): 896-904 DOI:10.1785/0220130189
(  0) 0) |
| [9] |
Guiraud M, Laborde O, Philip H. Characterization of Various Types of Deformation and Their Corresponding Deviatoric Stress Tensors Using Microfault Analysis[J]. Tectonophysics, 1989, 170(3-4): 289-316 DOI:10.1016/0040-1951(89)90277-1
(  0) 0) |
| [10] |
万永革, 盛书中, 许雅儒, 等. 不同应力状态和摩擦系数对综合P波辐射花样影响的模拟研究[J]. 地球物理学报, 2011, 54(4): 994-1 001 (Wan Yongge, Sheng Shuzhong, Hsu Yaju, et al. Effect of Stress Ratio and Friction Coefficient on Composite P Wave Radiation Patterns[J]. Chinese Journal of Geophysics, 2011, 54(4): 994-1 001 DOI:10.3969/j.issn.0001-5733.2011.04.014)
(  0) 0) |
| [11] |
McKenzie D P. The Relation between Fault Plane Solutions for Earthquakes and the Directions of the Principal Stresses[J]. Bulletin of the Seismological Society of America, 1969, 59(2): 591-601
(  0) 0) |
| [12] |
许忠淮, 阎明, 赵仲和. 由多个小地震推断的华北地区构造应力场的方向[J]. 地震学报, 1983, 5(3): 268-279 (Xu Zhonghuai, Yan Ming, Zhao Zhonghe. Evaluation of the Direction of Tectonic Stress in North China from Recorded Data of a Large Number of Small Earthquakes[J]. Acta Seismologica Sinica, 1983, 5(3): 268-279)
(  0) 0) |
| [13] |
岡田義光. 海沟型地震、内陆型地震和板内地震[J]. 世界地震译丛, 2007(2): 77-79 (Okada Y. Trench Earthquake, Inland Earthquake and Intraplate Earthquake[J]. Translated World Seismology, 2007(2): 77-79)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

