2. 华东交通大学土木工程国家实验教学示范中心, 南昌市双港东大街808 号, 330013
GNSS变形监测具有测站间无需通视和全天候自动观测等优点[1], 被广泛应用于工程结构的健康监测。由于数据采集过程中易受天气、树木遮挡、多路径效应等多种因素影响,GNSS变形序列中常包含测量噪声,这些噪声会严重影响测量精度,导致监测物的变形信息不准确。因此,有必要对监测数据进行滤波处理。常见的变形监测数据滤波方法有小波去噪[2-3]、Kalman滤波[4]、经验模态分解[5-8](empirical mode decomposition, EMD)等。GNSS变形监测受背景噪声影响具有非平稳、高频率、重复性强等特点,EMD及其改进方法在处理该类信号时具有明显优势。本文针对EMD分解中的噪声传递以及真实信号缺失等问题,提出基于EMD的改进方法——CEEMDAN, 在分解过程中加入有限次自适应白噪声,可有效避免模态混叠和信号失真。通过比较CEEMDAN、EMD和小波去噪方法的去噪效果,利用仿真数据与GNSS边坡实测监测数据进行实验分析,验证该方法的有效性和可靠性。
1 CEEMDAN方法构建 1.1 CEEMDAN原理EMD在构建包络线时使用三次样条法,无法判断信号两端是否为极值点,所以会产生端点效应。在分解过程中,EMD采取递归分解,在频率尺度不连续时,无法正确分离不同尺度的信号,从而造成模态混叠现象。针对该问题,EEMD分解时在序列中间断加入高斯白噪声,由于白噪声具有均值为0的特点,因此在加入数量足够多的情况下白噪声会相互抵消,从而在一定程度上避免模态混叠问题,但分解后的单个IMF仍存在残余噪声,导致残余噪声在高阶IMF和低阶IMF中传递。
CEEMDAN算法是在EEMD基础上发展而来的,针对EEMD分解过程中的噪声传递问题,CEEMDAN在各个分解阶段添加自适应高斯白噪声,得到模态分量后立即进行加总平均计算,同时在后续分解中执行同样操作。该算法可实现在较少的平均次数下,保证重构误差为0, 从而有效避免噪声传递的问题。CEEMDAN方法的具体步骤如下:
1) 在原始信号x(t)中添加I组均值为0的自适应白噪声ωi(t), 第i次信号可表示为:
| $x^{i}(t)=x(t)+\omega^{i}(t)$ | (1) |
式中,i为实验次数1, 2, …, I。采用EMD算法对xi(t)进行分解,得到第1个模态分量,然后立即对其进行加总平均计算,得到:
| $\mathrm{IMF}_{1}=\frac{1}{I} \sum\limits_{i=1}^{i} \mathrm{IMF}_{1}^{i}$ | (2) |
将原始信号减第1个模态分量得到残余分量:
| $r_{1}=x(t)-\mathrm{IMF}_{1}$ | (3) |
2) 求解第2阶模态分量IMF2, 在残余分量r1中继续加入白噪声ωi(t), 构成新的待分解信号:
| $R_{1}(t)=r_{1}(t)+\omega^{i}(t)$ | (4) |
进行i次实验(i=1, 2, …, I), 然后对R1(t)进行EMD分解,得到第2个模态分量:
| $\mathrm{IMF}_{2}=\frac{1}{I} \sum\limits_{i=1}^{i} \mathrm{IMF}_{2}^{i}$ | (5) |
残余分量可表示为:
| $\mathrm{IMF}_{2}=\frac{1}{I} \sum\limits_{i=1}^{i} \mathrm{IMF}_{2}^{i}$ | (6) |
3) 重复执行步骤1)和2), 直到信号不能再被分解,即信号单调为止,从而得到k个IMF, 信号x(t)可表示为:
| $x(t)=\sum\limits_{i=1}^{n} \mathrm{IMF}_{i}+r_{n}(t)$ | (7) |
排列熵(permutation entropy, PE)[9]、样本熵和模糊熵等概念相同,是衡量时间序列复杂程度的指标,在计算子序列之间复杂程度的同时可引入排列的思想。排列熵具有运算效率高、抗干扰能力强、输出结果简洁等优点,适用于非线性、不规则的信号,对区分IMF频率具有很好的适用性。时间序列越规则,其值越小;时间序列越复杂,即包含噪声越多,其值越大。计算排列熵的基本步骤如下:
1) 设时间长度为N的时间序列X(1), X(2), …, X(n), 重构时间序列,每个子序列以x(i)表示,得到以下序列矩阵:
| $\left[\begin{array}{cccc}x(1) & x(1+\lambda) & \cdots & x(1+(m-1)) \lambda \\ x(j) & x(j+\lambda) & \cdots & x(j+(m-1)) \lambda \\ \vdots & \vdots & & \vdots \\ x(k) & x(k+\lambda) & \cdots & x(k+(m-1)) \lambda\end{array}\right]$ | (8) |
式中,m为嵌入维数,λ为时间延迟,j=1, 2, …, k。
2) 将矩阵中每一行元素组成向量,按升序排列,即
| $\begin{aligned} X(i)=\{& x\left(i+\left(j_{1}-1\right) \lambda\right) \leqslant x\left(i+\left(j_{2}-1\right) \lambda\right) \\ & \left.\leqslant \cdots \leqslant x\left(i+\left(j_{m}-1\right) \lambda\right)\right\} \end{aligned}$ | (9) |
如果其中有2项相等,则按照ji的下标i进行排序,得到新的符号序列:
| $S(l)=\left(j_{1}, j_{2}, \cdots, j_{m}\right)$ | (10) |
式中,l=1, 2, …, k, 共产生m!种不同排列,即所有m维子序列X(i)都被映射到m!种不同排列中。
3) 计算所有符号的概率分布,用Pj表示,时间序列的排列熵可表示为:
| $H_{P}(m)=-\sum\limits_{j=1}^{k} P_{j} \ln P_{j}$ | (11) |
可以看出,当Pj取
| $H_{P}=H(m) / \ln (m !)$ | (12) |
式中,Hp的取值范围为[0, 1]。模糊隶属度为模糊集合中研究对象介于0~1之间的某个值,使用模糊隶属度区分高低频分量可得到较为合理的结果。本文基于IMF的特点,经过大量实验,参考文献[10]将PE值的模糊隶属度设定为0.6。当时间序列PE值大于0.6时,可认为是包含噪声的高频信号;PE值小于0.6时,则看作干净信号。计算每一个IMF的PE值,可以筛选出低频信号进行重构。
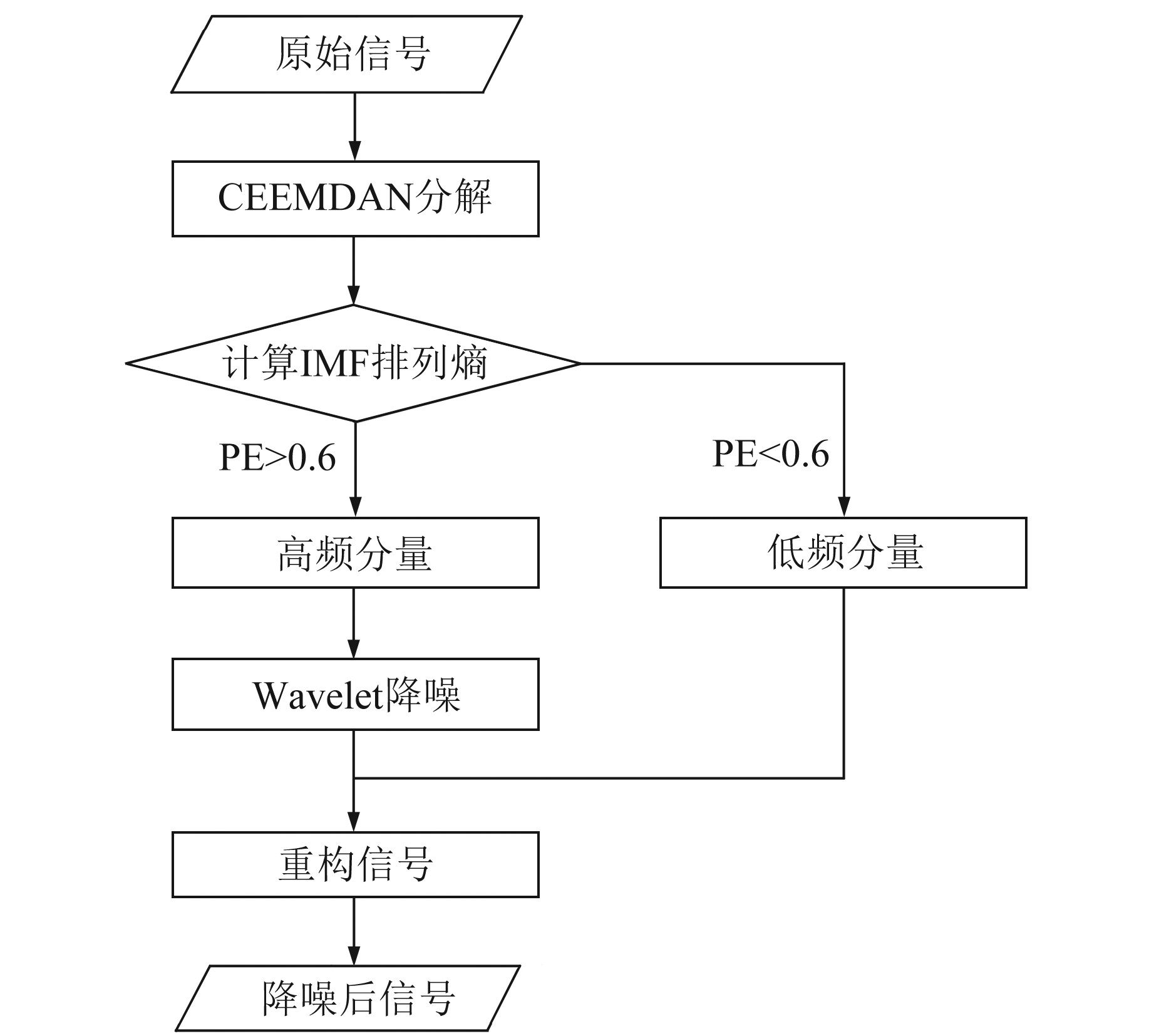
1.3 CEEMDAN去噪方法使用CEEMDAN将原始信号分解为不同频率的IMF分量,可避免EMD模态混叠和端点效应问题,分解得到的IMF分量能更清晰地表达自身特征。根据GNSS变形监测序列噪声高频率、周日重复的特点,可认为噪声主要存在于高频分量中,如果直接舍弃则可能丧失其中的真实信息。本文方法对高频分量继续进行小波去噪,使高频分量中的低频信息能得到很好地保留。首先需要找出高频分量与低频分量的分界点K, 常用方法有相关系数法、标准化模量累计均值法、平均周期与能量密度乘积法等。本文根据IMF的特性,引入排列熵的概念来区分高频噪声,计算每个IMF的PE值;然后筛选出高频分量,并将其看作噪声信号,将低频分量看作干净信号;对高频分量继续采用小波分析的方法进行去噪,同时对去噪后的高频分量与干净信号进行重构,得到去噪后的信号。具体步骤见图 1。
|
图 1 CEEMDAN方法流程 Fig. 1 Flow diagram of CEEMDAN method |
为验证本文方法的有效性,构造模拟变形信号对本文方法进行实验。模拟信号由3个正弦函数叠加组成,在该信号的基础上加入高斯白噪声,其函数为:
| $y_{t}=4 \sin (2 \pi t / 1000) \cdot \sin (2 \pi t / 400)+ \\ 2 \sin (2 \pi t / 600)+\sin (2 \pi t / 300)+\mathrm{ noise}$ | (13) |
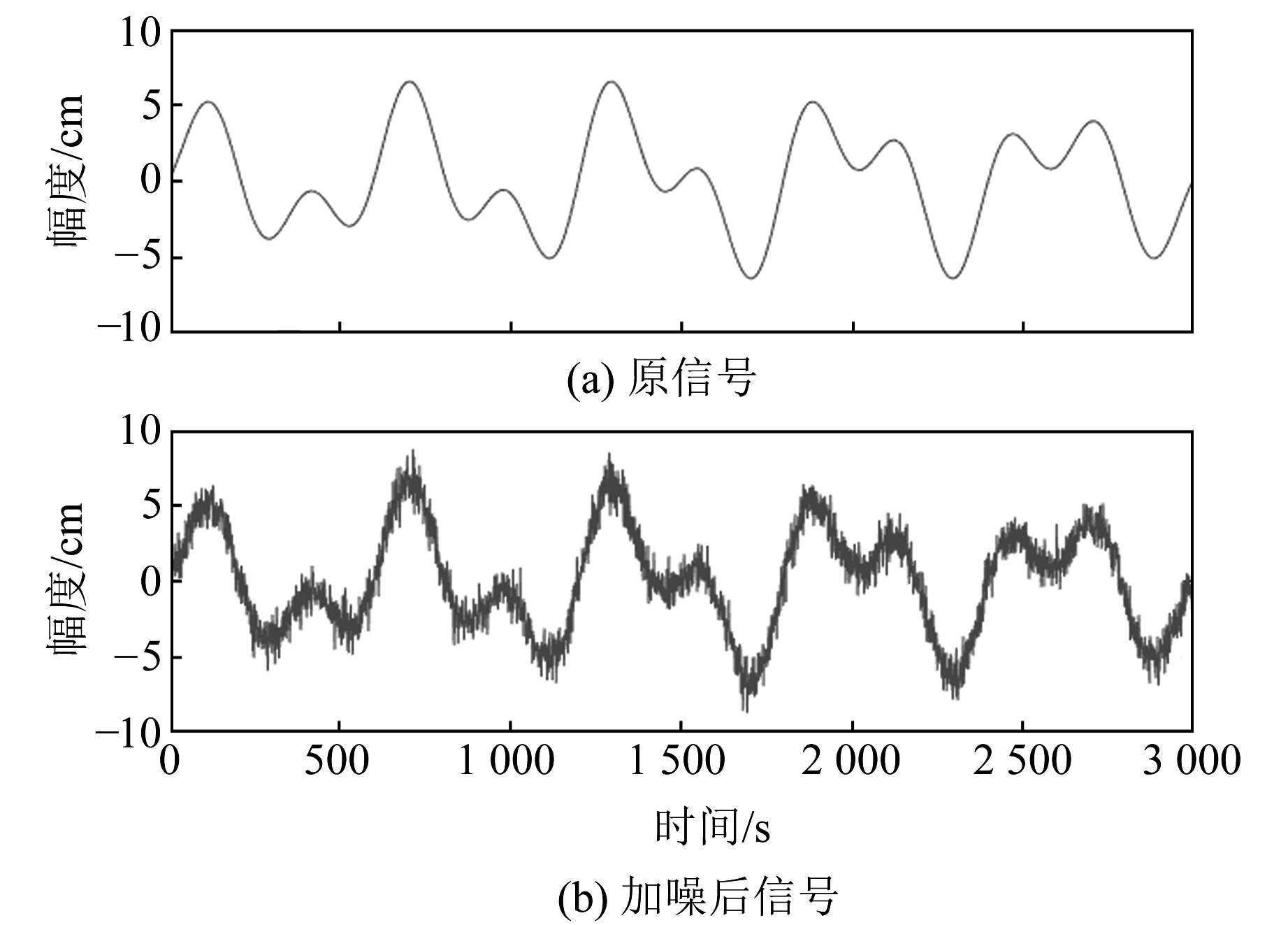
式中,noise是信噪比为2 dB的高斯白噪声,采样数为3 000, 采样间隔1 s, 仿真信号及加噪后信号如图 2所示。
|
图 2 仿真信号序列 Fig. 2 Simulation signal sequence diagram |
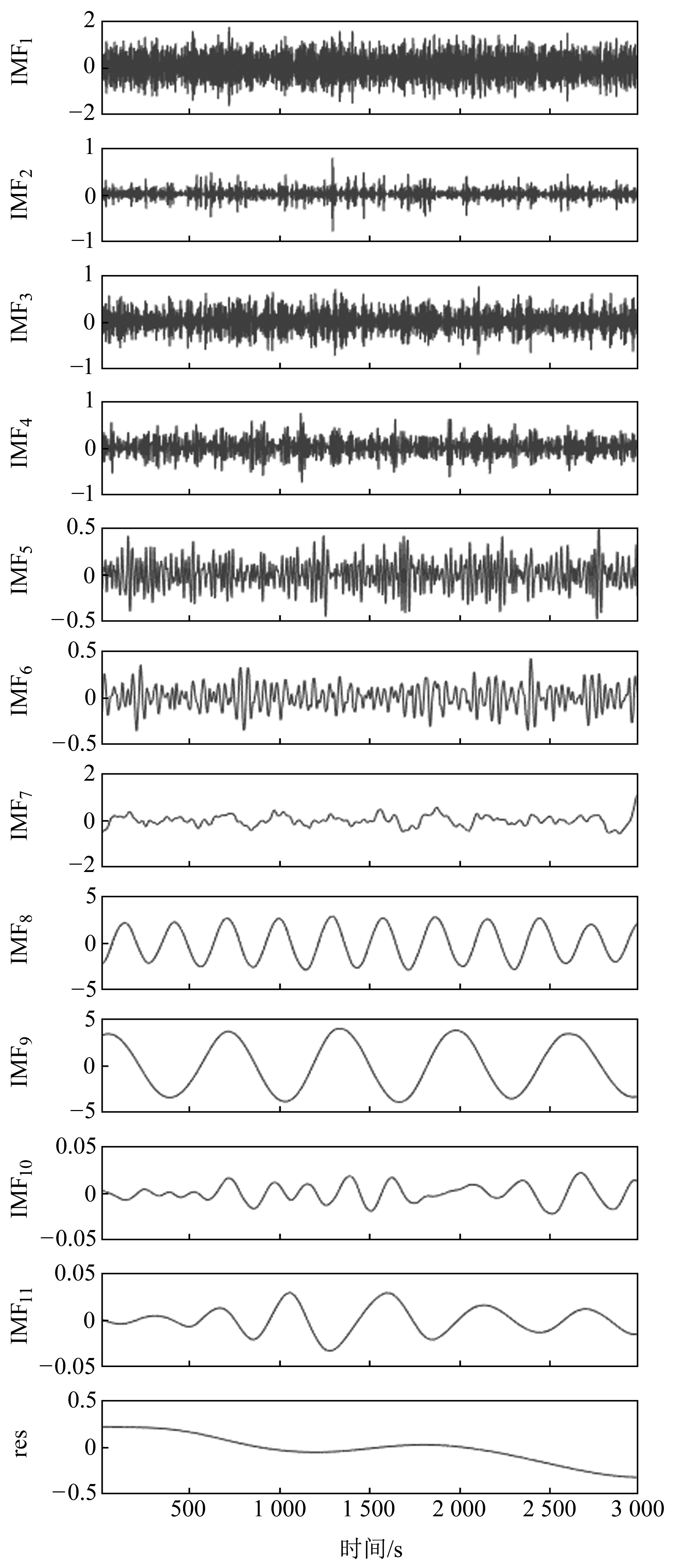
采用CEEMDAN算法对加噪后信号进行分解,得到11个IMF分量和1个残余项,各IMF分量如图 3所示。从图中可以看出,随着分解次数的增加,信号越来越平滑,表明高斯白噪声主要分布在高频分量上。
|
图 3 基于CEEMDAN方法的分解图 Fig. 3 Decomposition diagram based on CEEMDAN method |
利用排列熵理论确定高频噪声,计算各IMF分量的PE值,结果见表 1。由表 1可知,前3个IMF分量的PE值大于0.6, 可将其看作高频噪声,使用小波变换进行去噪处理。经过多次实验,小波基选择去噪效果较好的db7小波,分解层数为3, 选取Heursure(启发式阈值)进行软阈值处理。将去噪后的分量与第4~11个低频分量和残余项进行重构,得到去噪后信号。
|
|
表 1 各IMF分量排列熵 Tab. 1 The permutation entropy of each IMF |
为验证CEEMDAN方法的去噪效果,对原始信号分别采用小波去噪、EMD、CEEMDAN方法进行去噪,利用信噪比、均方根误差和相关系数3个指标评价去噪效果:
| $\mathrm{SNR}=10 \lg \left(\frac{\sum\limits_{i=1}^{L} s^{2}(i)}{\sum\limits_{i=1}^{L}\left(s(i)-s^{\prime}(i)^{2}\right.}\right)$ | (14) |
| $\mathrm{RMES}=\sqrt{\frac{1}{L}\left(s(i)-s^{\prime}(i)\right)^{2}}$ | (15) |
| $R=\frac{\operatorname{cov}\left(s, s^{\prime}\right)}{\sigma_{s} \cdot \sigma_{s^{\prime}}}$ | (16) |
式中,SNR为信噪比,RMSE为均方根误差,R为相关系数,s(i)为原始信号,s′(i)为去噪后信号,L为信号长度。具体去噪效果见表 2, 从表中可以看出,小波去噪和EMD方法均能起到一定的去噪效果。与之相比,CEEMDAN方法去噪后的信噪比、相关系数均有所提升,均方误差有所降低,表明本文方法具有有效性。
|
|
表 2 仿真数据去噪效果对比 Tab. 2 Comparison of denoising effect of simulation data |
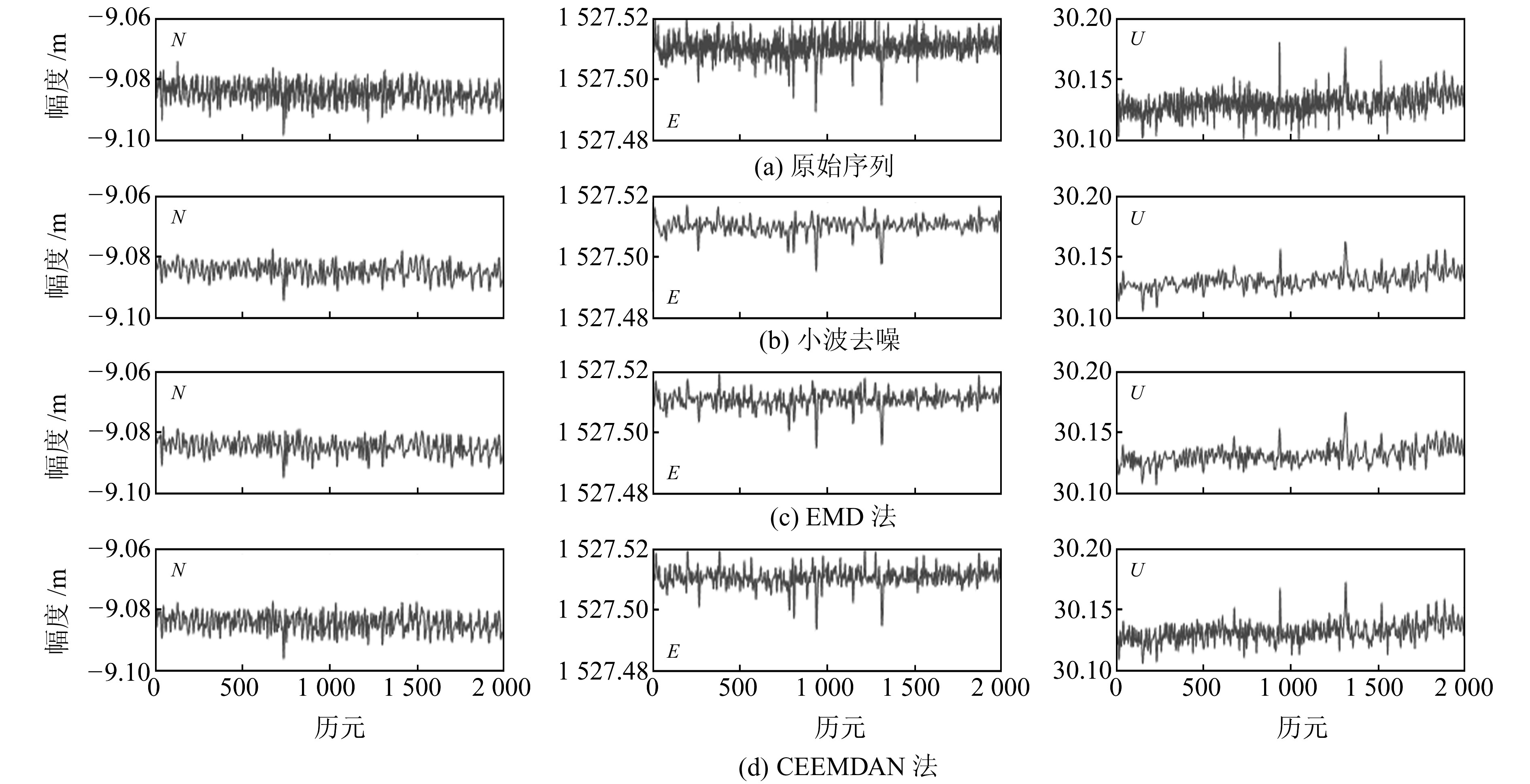
为进一步验证该方法的可靠性,利用某边坡GNSS变形监测数据进行实验分析。该边坡布设0001、0007、J001、J002共4个监测点,采样频率为1 Hz。实验利用09-01~11-30共91 d的监测数据,选取间隔1 h, 截取2 000个历元进行去噪处理。由于篇幅所限,仅展示0001监测点的去噪结果,原始序列和去噪后序列如图 4所示,表 3为0001监测点N、E、U方向3种去噪方法的效果对比。
|
图 4 实测数据去噪效果 Fig. 4 Denoising effect of measured data |
|
|
表 3 实测数据降噪效果对比 Tab. 3 Comparison of denoising effect of measured data |
从图 4和表 3可以看出,原始监测序列局部呈不平稳态势,具有很大随机性,说明其受到很大的噪声污染。通过分析3个方向的信噪比和相关系数可知,新方法与小波去噪方法相比,信噪比分别提高7.41%、3.15%和6.22%, 相关系数分别提高19.6%、27.34%和23.13%;与EMD方法相比,信噪比分别提高6.86%、2.31%和5.97%, 相关系数分别提高16.67%、15.64%和21.22%, 表明新方法相比于传统方法可提取更多的变形量,与原始序列更接近。从均方根误差来看,3个方向上,新方法与小波去噪方法相比分别减少47.37%、36%和40%, 与EMD方法相比分别减少6.86%、2.31%和5.97%, 表明新方法的去噪效果更稳定,能更清晰地表达变形趋势。
4 结语本文构建了一种自适应完备集合经验模态分解的去噪方法,引入排列熵理论确定高低频分界值K。该方法结合多种方法的优点,可有效解决EMD分析的端点效应和模态混叠问题,通过排列熵理论准确划分高低频,对高频噪声进行精细处理,使其GNSS变形监测的真实信息得到有效保留。仿真和实测数据实验表明,CEEMDAN方法的去噪精度显著优于EMD和小波去噪方法,证明了其有效性和可靠性。
| [1] |
陈永奇. 工程测量学[M]. 北京: 测绘出版社, 2016 (Chen Yongqi. Engineering Surveying[M]. Beijing: Surveying and Mapping Press, 2016)
(  0) 0) |
| [2] |
李超, 郝建新, 文鸿雁, 等. 变形监测数据的一种小波去噪法研究[J]. 测绘科学, 2012, 37(4): 24-25 (Li Chao, Hao Jianxin, Wen Hongyan, et al. A Wavelet De-Noising Method of Deformation Monitoring Data[J]. Science of Surveying and Mapping, 2012, 37(4): 24-25)
(  0) 0) |
| [3] |
甘若, 陈天伟, 郑旭东, 等. 改进小波阈值函数在变形监测数据去噪中的应用[J]. 桂林理工大学学报, 2020, 40(1): 150-155 (Gan Ruo, Chen Tianwei, Zheng Xudong, et al. Wavelet Deformation Monitoring Data of Denoising Algorithm Based on New Threshold Function[J]. Journal of Guilin University of Technology, 2020, 40(1): 150-155)
(  0) 0) |
| [4] |
雷孟飞, 孔超, 周俊华. 自适应卡尔曼滤波在BDS变形监测数据处理中的应用[J]. 导航定位学报, 2019, 7(4): 75-79 (Lei Mengfei, Kong Chao, Zhou Junhua. Application of Adaptive Kalman Filtering in BDS Deformation Monitoring Data Processing[J]. Journal of Navigation and Positioning, 2019, 7(4): 75-79)
(  0) 0) |
| [5] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1 971): 903-995
(  0) 0) |
| [6] |
张双成, 何月帆, 李振宇, 等. EMD用于GPS时间序列降噪分析[J]. 大地测量与地球动力学, 2017, 37(12): 1 248-1 252 (Zhang Shuangcheng, He Yuefan, Li Zhenyu, et al. EMD for Noise Reduction of GPS Time Series[J]. Journal of Geodesy and Geodynamics, 2017, 37(12): 1 248-1 252)
(  0) 0) |
| [7] |
钱荣荣, 王坚, 刘立聪. 基于完备经验模态分解自相关消噪技术的GNSS高精度动态变形监测研究[J]. 大地测量与地球动力学, 2017, 37(6): 623-626 (Qian Rongrong, Wang Jian, Liu Licong. GNSS High Precision Dynamic Deformation Monitoring Research Based on CEEMD Auto Correlation De-Noising Technique[J]. Journal of Geodesy and Geodynamics, 2017, 37(6): 623-626)
(  0) 0) |
| [8] |
罗亦泳, 黄城, 张静影. 基于变分模态分解的变形监测数据去噪方法[J]. 武汉大学学报: 信息科学版, 2020, 45(5): 784-790 (Luo Yiyong, Huang Cheng, Zhang Jingying. Denoising Method of Deformation Monitoring Data Based on Variational Mode Decomposition[J]. Geomatics and Information Science of Wuhan University, 2020, 45(5): 784-790)
(  0) 0) |
| [9] |
Bandt C, Pompe B. Permutation Entropy: A Natural Complexity Measure for Time Series[J]. Physical Review Letters, 2002, 88(17)
(  0) 0) |
| [10] |
郑近德, 程军圣, 杨宇. 改进的EEMD算法及其应用研究[J]. 振动与冲击, 2013, 32(21): 21-26 (Zheng Jinde, Cheng Junsheng, Yang Yu. Modified EEMD Algorithm and Its Applications[J]. Journal of Vibration and Shock, 2013, 32(21): 21-26)
(  0) 0) |
2. National Experimental Teaching Demonstration Center of Civil Engineering, East China Jiaotong University, 808 East-Shuanggang Street, Nanchang 330013, China
 2021, Vol. 41
2021, Vol. 41

