短基线集干涉合成孔径雷达(SBAS-InSAR)技术在地震、火山、滑坡、泥石流、城市沉降、河口沉降等灾害监测中有广泛应用[1-4]。然而在实际使用中发现,SBAS-InSAR形变模型病态的可能性始终存在,这会直接影响形变反演的精度和可靠性[5-6]。
谱修正迭代法优良的性质及其未改变方程等量关系的特点,使其在病态问题的解算中得到广泛关注[7-12]。通过谱修正迭代的收敛性证明不难看出,其充分迭代结果收敛于最小二乘估计结果,现有的迭代终止条件一般是根据相邻两次迭代估值是否小于阈值进行判定,但这意味着不同的阈值会导致谱修正迭代估计结果发生变化,这种经验性的阈值选取会带来较大的不确定性。因此,本文针对谱修正迭代终止条件的优化方法展开研究,提出一种L曲线谱修正迭代法实现迭代结果的优选,并通过SBAS-InSAR形变反演实验对方法的有效性进行验证。
1 SBAS-InSAR形变反演假设实验区域内存在Ns+1幅时间序列为t0, t1, …, tNs的单视复数(singal look complex, SLC)影像(图 1), 根据时空基线条件得到M个差分干涉对。若第j幅干涉图由tA和tB(tA > tB)时刻的影像得到,去除地形相位可得到差分干涉图中(r, x)处的差分干涉相位为:

|
图 1 SBAS-InSAR时序差分干涉对的组成方式 Fig. 1 Combination of time series differential interference pairs of SBAS-InSAR |
| $\delta \varphi_{j}(r, x)=\varphi\left(t_{B}, r, x\right)-\varphi\left(t_{A}, r, x\right)$ | (1) |
| $\delta \varphi_{j}(r, x) \approx \frac{4 \pi}{\lambda}\left[d\left(t_{B}, r, x\right)-d\left(t_{A}, r, x\right)\right]+ \\ \varphi_{\text {atm }}+\varphi_{\text {non-lin }}+\varphi_{\text {noise }}+\varphi_{\text {top-error }}$ | (2) |
式中,d(tA, r, x)和d(tB, r, x)为LOS向累积形变量,φ(tA, r, x)和φ(tB, r, x)为形变相位值,λ为雷达波长,φatm为大气延迟相位,φnon-lin为非线性形变相位,φnoise为噪声相位,φtop-error为地形残余相位。
不同时刻(t0, t1, …, tNs)相对于t0时刻的形变相位向量φT可表示为:
| $\boldsymbol{\varphi}^{\mathrm{T}}=\left[\varphi\left(t_{1}\right), \cdots, \varphi\left(t_{N_{s}}\right)\right]$ | (3) |
差分干涉图解缠后的相位观测值δφT可表示为:
| $\delta \boldsymbol{\varphi}^{\mathrm{T}}=\left[\delta \varphi_{1}, \cdots, \delta \varphi_{N_{s}}\right]$ | (4) |
通过组合差分干涉图可得:
| $\underset{M \times 1}{\delta \hat{\boldsymbol{\varphi}}}=\underset{M \times N_{s}}{\boldsymbol{B}} \underset{N_{s} \times 1} {\hat{\boldsymbol{\varphi}}_{}}$ | (5) |
式中,
| $\hat{\boldsymbol{\varphi}}=\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}} \delta \boldsymbol{\varphi}$ | (6) |
不难看出,时序差分干涉对的质量对形变反演精度有着重要影响。由于产生时序差分干涉对的方法仍以经验判断为主,因此形变反演模型中可能存在病态性,从而导致最小二乘估计结果难以满足精度要求。
2 谱修正迭代法设X的估值为
| $\boldsymbol{V}=\boldsymbol{B} \hat{\boldsymbol{X}}-\boldsymbol{L}$ | (7) |
法方程为:
| $\boldsymbol{N} \hat{\boldsymbol{X}}=\boldsymbol{W}$ | (8) |
式中,N=BTPB, W=BTPL, L为观测向量,P为权阵。
在法方程两侧加上$\boldsymbol{N} \hat{\boldsymbol{X}}=\boldsymbol{W}$, 可得:
| $(\boldsymbol{N}+\boldsymbol{I}) \hat{\boldsymbol{X}}=\boldsymbol{W}+\hat{\boldsymbol{X}}$ | (9) |
式中,I为单位阵。则谱修正迭代法的公式为:
| $\hat{\boldsymbol{X}}^{(i)}=(\boldsymbol{N}+\boldsymbol{I})^{-1}\left(\boldsymbol{W}+\hat{\boldsymbol{X}}^{(i-1)}\right)$ | (10) |
式中,
| $\boldsymbol{L}=\boldsymbol{A} \boldsymbol{Y}+\boldsymbol{\Delta}$ | (11) |
| $\hat{\boldsymbol{Y}}=\boldsymbol{\Lambda}^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{L}$ | (12) |
因为有
| $\hat{\boldsymbol{Y}}^{(i)} \triangleq \boldsymbol{F}_{i} \hat{\boldsymbol{Y}}+(\boldsymbol{\Lambda}+\boldsymbol{I})^{-i} \hat{\boldsymbol{Y}}^{(0)}$ | (13) |
式中,i为迭代次数,i=1, 2, …, Fi为n阶对角矩阵。设Fi(r)为对角矩阵Fi的第r个对角元素,r=1, 2, …, n,
| $F_{i}^{(r)}=\frac{\left(\lambda_{i}^{2}+1\right)^{i}-1}{\left(\lambda_{i}^{2}+1\right)^{i}}$ | (14) |
由于谱修正迭代法最终收敛于最小二乘估计[7-9], 当谱修正迭代法的迭代初值给定后,可得:
| $E\left(\hat{\boldsymbol{Y}}^{(i)}\right)=\frac{(\boldsymbol{\Lambda}+\boldsymbol{I})^{i}-1}{(\boldsymbol{\Lambda}+\boldsymbol{I})^{i}} \tilde{\boldsymbol{Y}}+(\boldsymbol{\Lambda}+\boldsymbol{I})^{-i} \hat{\boldsymbol{Y}}^{(0)}$ | (15) |
| $\operatorname{cov}\left(\hat{\boldsymbol{Y}}^{(i)}\right)=\sigma_{0}^{2} \boldsymbol{F}_{j} \boldsymbol{\Lambda}^{-1} \boldsymbol{F}_{j}$ | (16) |
则谱修正迭代法最终估值的均方误差可表示为:
| $\operatorname{MSE}\left(\hat{\boldsymbol{X}}^{(i)}\right)=\sum\limits_{r=1}^{n}\left(\left(F_{i}^{(r)}-1\right) \tilde{\boldsymbol{Y}}+\frac{\hat{\boldsymbol{Y}}^{(0)}}{\left(\lambda_{r}^{2}+1\right)^{i}}\right)^{2}+ \\ \sigma_{0}^{2} \sum\limits_{r=1}^{n} \frac{\left(F_{i}^{(r)}\right)^{2}}{\lambda_{i}^{2}}$ | (17) |
有偏估计方法通常是引入正则化参数或正则化矩阵,通过降低解算方程的病态程度,从而降低病态性对估计结果的影响程度。而谱修正迭代法在不改变方程等量关系的情况下,通过合理确定迭代估计结果改善病态问题估计的结果。
3 L曲线谱修正迭代谱修正迭代法的迭代终止条件直接影响估计结果的精度。通过设置阈值确定谱修正迭代法终止条件,易使得估计结果的稳定性变差,估值精度存在不确定性。因此,有必要改进谱修正迭代法的迭代终止条件。
令迭代初始值为
| $\hat{\boldsymbol{X}}^{(i)}=\boldsymbol{N}_{P} \boldsymbol{W}+\cdots+\underbrace{\boldsymbol{N}_{P} \cdots \boldsymbol{N}_{P}}_{i} \boldsymbol{W}+\underbrace{\boldsymbol{N}_{P} \cdots \boldsymbol{N}_{P}}_{i} \hat{\boldsymbol{X}}^{(0)}$ | (18) |
可以看出,谱修正迭代法的迭代估值
为了实现谱修正迭代结果的优选,提出一种L曲线谱修正迭代法,利用L曲线的最大曲率点,确定残差较小且稳定的迭代结果作为最终估值。构造谱修正迭代法的估计准则为:
| $\|\boldsymbol{B} \hat{\boldsymbol{X}}-\boldsymbol{L}\|^{2}+i \hat{\boldsymbol{X}}^{\mathrm{T}} \hat{\boldsymbol{X}}=\|\boldsymbol{B} \hat{\boldsymbol{X}}-\boldsymbol{L}\|^{2}+ \\ i\|\hat{\boldsymbol{X}}\|^{2}=\min$ | (19) |
其中,
定义
| $\hat{\rho}=\lg \|\boldsymbol{B} \hat{\boldsymbol{X}}-\boldsymbol{L}\|_{2}^{2}=2 \lg \|\boldsymbol{B} \hat{\boldsymbol{X}}-\boldsymbol{L}\|_{2}$ | (20) |
| $\hat{\eta}=\lg \|\hat{\boldsymbol{x}}\|_{2}^{2}=2 \lg \|\hat{\boldsymbol{x}}\|_{2}$ | (21) |
令
| $\kappa=2 \frac{\hat{\rho}^{\prime} \hat{\eta}^{\prime \prime}+\hat{\rho}^{\prime \prime} \hat{\eta}^{\prime}}{\left(\left(\hat{\rho}^{\prime}\right)^{2}+\left(\hat{\eta}^{\prime}\right)^{2}\right)^{3 / 2}}$ | (22) |
选择最大曲率点作为终止迭代的条件,迭代次数m对应的估计值即为估值稳定且残差较小的谱修正迭代法的最终估值。
基于L曲线的谱修正迭代法的计算流程如图 2所示,计算步骤为:1)进行谱修正充分迭代,当迭代估值
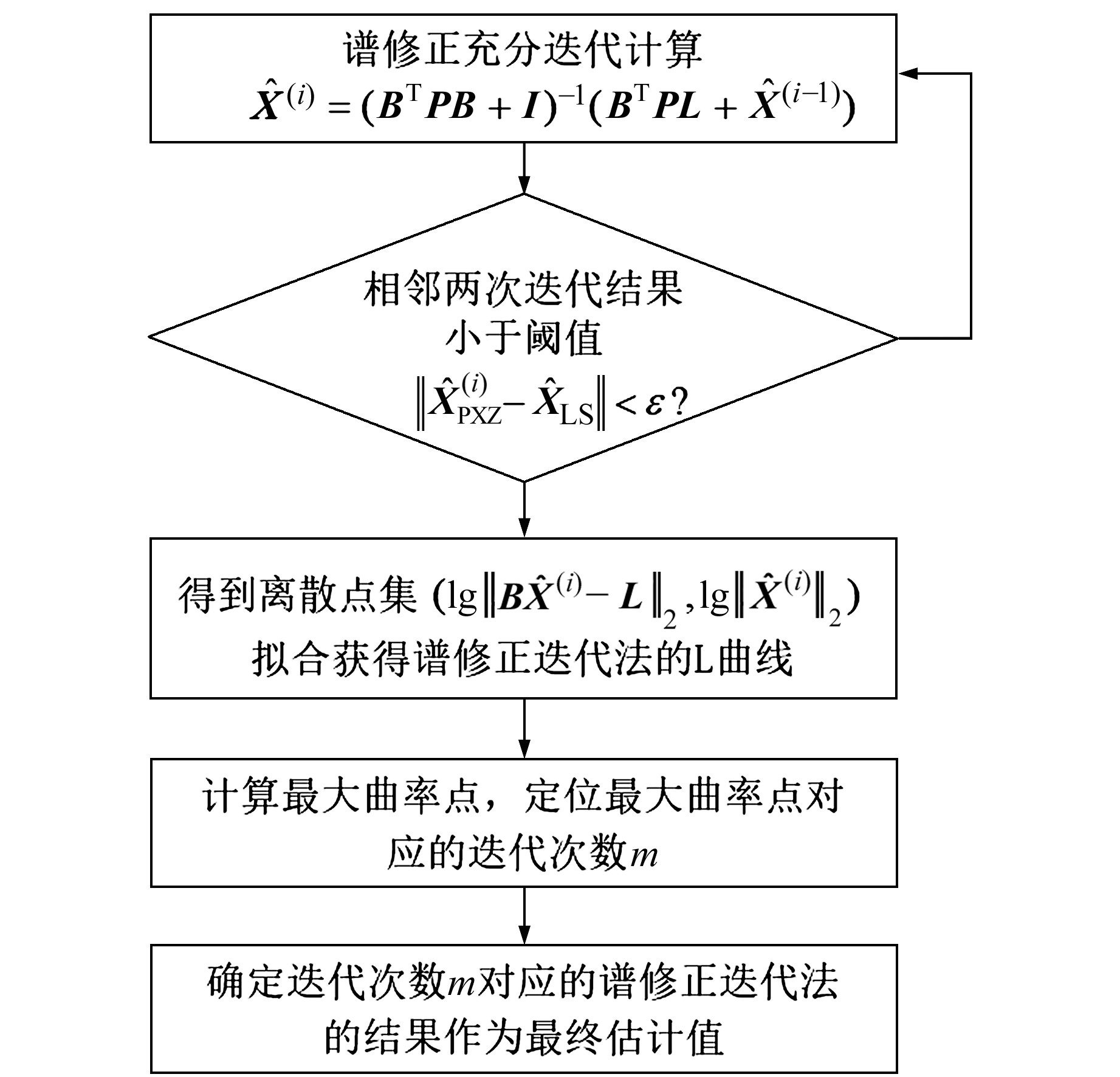
|
图 2 基于L曲线的谱修正迭代法 Fig. 2 L-curve characteristic value correction iteration method |
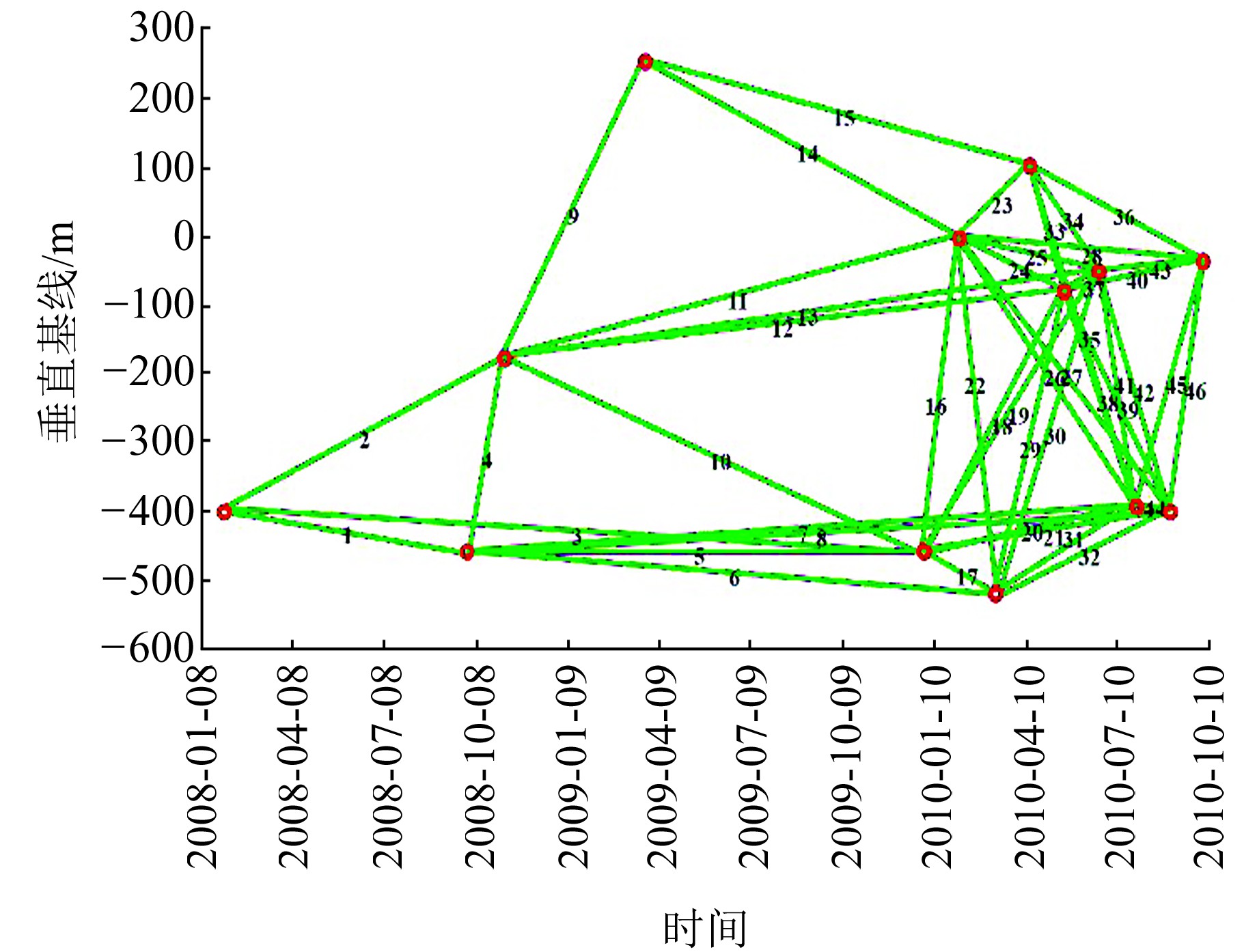
济宁市拥有丰富的煤炭资源,但随着开采量的增加,矿区沉降问题日益严重[13]。采用2008-01~2010-09期间覆盖实验区的13景Envisat ASAR影像(极化方式VV, 波段C, 波束入射角23°, 方位向分辨率4 m, 距离向分辨率7 m), 采用多主影像自由组合进行干涉配对,形成46个干涉对(图 3), 选取58 751个高相干点,构建形变模型系数矩阵的条件数为519, 呈病态性。研究区域内既有沉降,也存在抬升,最大年平均沉降速率大于-40 mm/a。
|
图 3 干涉对组合方式 Fig. 3 Combination of interference pairs |
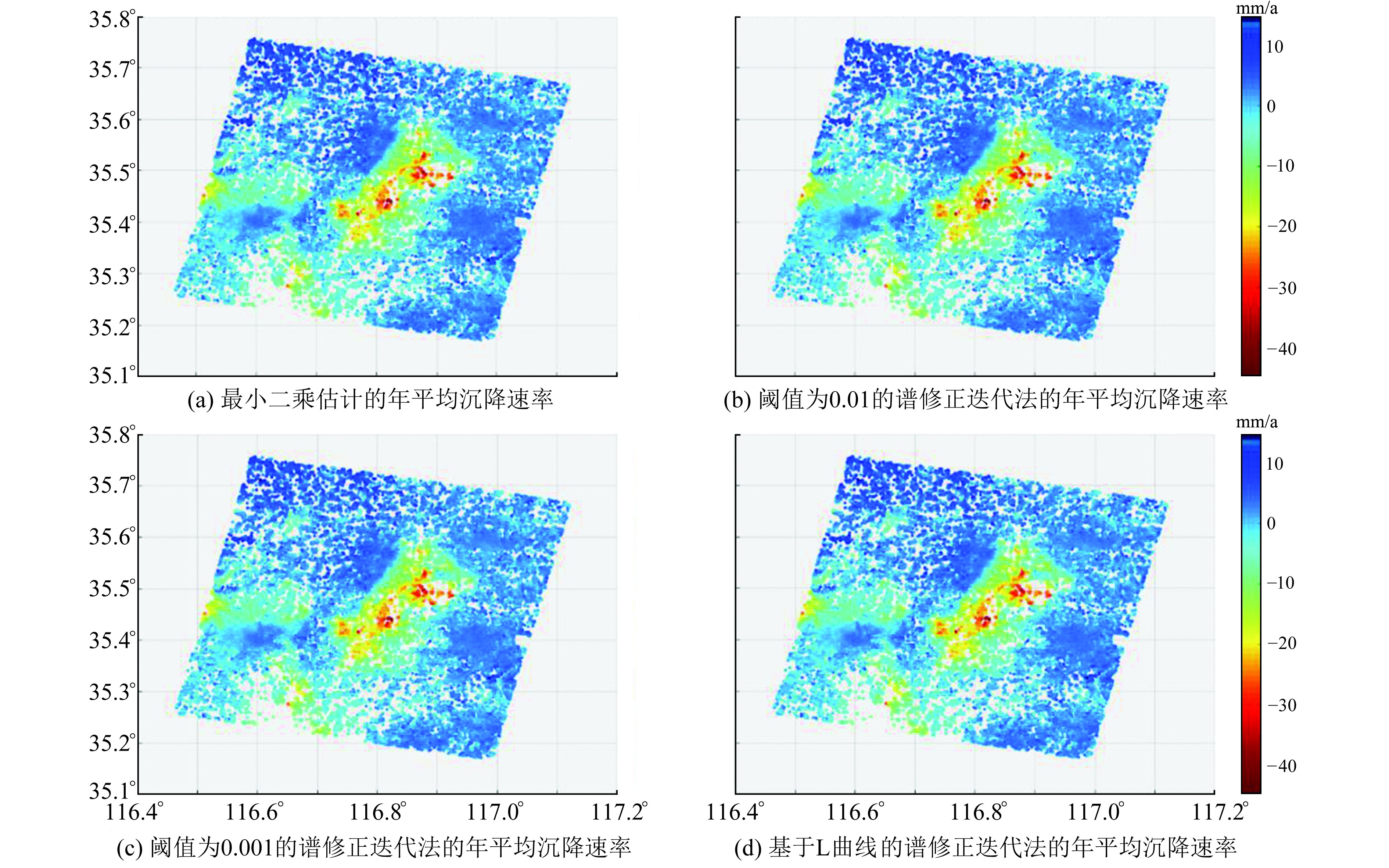
采用最小二乘估计(LS)、谱修正迭代法(PXZ, 阈值为0.01、0.001)、L曲线谱修正迭代法(PXZ-L)进行解算,图 4给出了不同估计方法的年平均沉降速率。表 1为LS、PXZ-0.01、PXZ-0.001、PXZ-L解算的高相干点的均方根误差统计结果。将实验区内5个点的水准数据作为精度评定的依据,表 2和3分别列出4种方法相对于水准结果的沉降量和沉降速率中误差。所选5个水准点位于沉降区域的边缘,最大年平均沉降速率均小于-6 mm/a。
|
图 4 不同估计方法解算得到的年平均沉降速率 Fig. 4 Annual average subsidence rate calculated by different estimation methods |
由图 4可知,最小二乘估计的年平均沉降速率范围为-43.91~14.94mm/a; 谱修正迭代法(阈值分别为0.01、0.001)的年平均沉降速率范围为-43.70~14.70 mm/a、-43.88~14.87mm/a; L曲线谱修正迭代法的年平均沉降速率范围为-48.90~14.89 mm/a。可见,受病态影响,各种方法的估计结果存在差异。
|
|
表 1 均方根误差统计 Tab. 1 Statistical table of root mean square error |
|
|
表 2 不同估计方法解算的沉降量与水准点监测结果的差值 Tab. 2 The differences of settlement calculated bydifferent estimation methods and levelling monitoring |
|
|
表 3 不同估计方法解算的年平均沉降速率与水准点监测结果的差值 Tab. 3 The differences of subsidence rate calculated by different estimation methods and levelling monitoring |
由表 1可以看出,形变反演结果的均方根误差集中分布于0~15 mm之间,最小二乘估计、谱修正迭代法(阈值为0.01、0.001)、L曲线谱修正迭代法的较小均方根误差频数占比分别为97.82%、97.85%、97.82%和97.88%。因此,不同阈值条件下的谱修正迭代法的估计结果存在差异,使得对病态问题的改善程度存在较大不确定性;而L曲线谱修正迭代法通过选择估值稳定且残差较小的估计结果,实现了估计结果的优选,其较小均方根误差频数占比也最高。
比较表 2中水准监测结果与各估计方法反演得到的最邻近高相干点的沉降量差值可以看出,谱修正迭代法(阈值为0.01、0.001)以及L曲线谱修正迭代法反演后的沉降量结果依次为σPXZ-0.01=2.908 mm, σPXZ-0.001=2.977 mm及σPXZ-L=2.867 mm, 小于最小二乘估计方法反演得到的沉降量结果σLS=3.035 mm。表 3中各方法估计的年平均沉降速率差值结果显示,3种方法估计的沉降速率结果依次为σPXZ-0.01=1.077 mm/a, σPXZ-0.001=1.103 mm/a及σPXZ-L=1.062 mm/a, 同样小于最小二乘方法估计的沉降速率结果σLS=1.124 mm/a。沉降量与沉降速率的结果均表明,谱修正迭代法可减弱病态性对估计结果的不良影响,其中,基于L曲线的谱修正迭代法的差值最小,证明L曲线谱修正迭代法是可行的。
5 结语谱修正迭代法通过在法方程系数矩阵的两端同时增加未知参数,在不改变方程等量关系的情况下,实现对系数矩阵病态性的改善,在整个计算过程中不需要额外计算正则化参数或正则化矩阵,因此在病态问题的解算中具有独特的优势。但谱修正迭代终止条件通常是依据相邻迭代结果小于阈值,而阈值的选取越小,迭代结果越接近于最小二乘估计,因此基于阈值的迭代终止条件无益于估计结果的优选。为此,本文提出一种利用L曲线进行谱修正迭代估值优选的方法,并通过SBAS-InSAR形变模型反演实验进行验证分析。结果表明,基于L曲线的谱修正迭代法能够提高解的精度和可靠性。
| [1] |
Canova F, Tolomei C, Salvi S, et al. Land Subsidence along the Ionian Coast of SE Sicily(Italy), Detection and Analysis via Small Baseline Subset(SBAS)Multitemporal Differential SAR Interferometry[J]. Earth Surface Processes and Landforms, 2012, 37(3): 273-286 DOI:10.1002/esp.2238
(  0) 0) |
| [2] |
李金超, 高飞, 鲁加国, 等. 基于SBAS-InSAR和GM-SVR的居民区形变监测与预测[J]. 大地测量与地球动力学, 2019, 39(8): 837-842 (Li Jinchao, Gao Fei, Lu Jiaguo, et al. Deformation Monitoring and Prediction of Residential Areas Based on SBAS-InSAR and GM-SVR[J]. Journal of Geodesy and Geodynamics, 2019, 39(8): 837-842)
(  0) 0) |
| [3] |
高二涛, 范冬林, 付波霖, 等. 基于PS-InSAR和SBAS技术监测南京市地面沉降[J]. 大地测量与地球动力学, 2019, 39(2): 158-163 (Gao Ertao, Fan Donglin, Fu Bolin, et al. Land Subsidence Monitoring of Nanjing Area Based on PS-InSAR and SBAS Technology[J]. Journal of Geodesy and Geodynamics, 2019, 39(2): 158-163)
(  0) 0) |
| [4] |
莫莹, 朱煜峰, 江利明, 等. 基于Sentinel-1A的南昌市时间序列InSAR地面沉降监测[J]. 大地测量与地球动力学, 2020, 40(3): 270-275 (Mo Ying, Zhu Yufeng, Jiang Liming, et al. Land Subsidence Monitoring of Nanchang Area Based on Sentinel-1A Using Time Series InSAR Technology[J]. Journal of Geodesy and Geodynamics, 2020, 40(3): 270-275)
(  0) 0) |
| [5] |
Zhai M, Liu G L, Tao Q X, et al. Application of the Liu-Type Estimator in Illposed Problems of Small Baseline Subsets Deformation Monitoring[J]. Journal of Applied Remote Sensing, 2018, 12(3)
(  0) 0) |
| [6] |
Zhai M, Liu G L, Tao Q X, et al. A Novel Approach for Regularization Matrix Construction and Its Application in SBAS Deformation Model Inversion[J]. International Journal of Remote Sensing, 2020, 41(10): 3 708-3 722 DOI:10.1080/01431161.2019.1707900
(  0) 0) |
| [7] |
王新洲, 刘丁酉, 张前勇, 等. 谱修正迭代法及其在测量数据处理中的应用[J]. 黑龙江工程学院学报, 2001, 15(2): 3-6 (Wang Xinzhou, Liu Dingyou, Zhang Qianyong, et al. The Iteration by Correcting Characteristic Value and Its Application in Surveying Data Processing[J]. Journal of Heilongjiang Institute of Technology, 2001, 15(2): 3-6)
(  0) 0) |
| [8] |
王新洲, 刘丁酉, 黄海兰. 谱修正迭代结果的协因数矩阵[J]. 武汉大学学报: 信息科学版, 2003, 28(4): 429-431 (Wang Xinzhou, Liu Dingyou, Huang Hailan. The Co-Factor Matrix of the Iteration Method by Correcting Characteristic Value[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 429-431)
(  0) 0) |
| [9] |
Zhai M, Liu G L, Tao Q X, et al. A Novel Characteristic Value Correction Iteration Method[J]. Communications in Statistics-Simulation and Computation, 2019, 48(2): 591-600 DOI:10.1080/03610918.2017.1390124
(  0) 0) |
| [10] |
邓兴升, 孙虹虹. 自适应谱修正LU分解法解算高病态法方程[J]. 大地测量与地球动力学, 2014, 34(6): 135-139 (Deng Xingsheng, Sun Honghong. Self-Adaptive Spectrum Correction LU Decomposition Algorithm for Solving a Normal Equation with Severely Ill-Conditioned Matrix[J]. Journal of Geodesy and Geodynamics, 2014, 34(6): 135-139)
(  0) 0) |
| [11] |
于冬冬, 王乐洋. 病态总体最小二乘问题的谱修正迭代法[J]. 大地测量与地球动力学, 2015, 35(4): 702-706 (Yu Dongdong, Wang Leyang. Iteration Method by Correcting Characteristic Values to Ill-Posed Total Least Squares Problem[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 702-706)
(  0) 0) |
| [12] |
蒋攀, 游为. 基于实四元数的大旋转角三维坐标转换的改进谱修正迭代解法[J]. 大地测量与地球动力学, 2019, 39(11): 1 182-1 187 (Jiang Pan, You Wei. The Improved Iteration Method by Correcting Characteristic Value for Transformation of Three-Dimensional Coordinates Based on Large Rotation Angle and Quaternions[J]. Journal of Geodesy and Geodynamics, 2019, 39(11): 1 182-1 187)
(  0) 0) |
| [13] |
王志勇, 张继贤, 黄国满. 基于InSAR的济宁矿区沉降精细化监测与分析[J]. 中国矿业大学学报, 2014, 43(1): 169-174 (Wang Zhiyong, Zhang Jixian, Huang Guoman. Precise Monitoring and Analysis of the Land Subsidence in Jining Coal Mining Area Based on InSAR Technique[J]. Journal of China University of Mining and Technology, 2014, 43(1): 169-174)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


