利用GPS技术反演海潮负荷位移参数主要分为静态方法和动态方法。例如吴志露等[1]利用傅里叶变换从动态PPP解算的时间序列中提取出潮波参数,解算结果证明了GPS反演有效、可靠,然而其解算过程中忽略了时间序列长度以及地心运动改正对潮波参数的影响;魏国光等[2]证明,短期静态PPP解算结果中提取的潮波参数可用于补充观测资料的不足,但由于其静态PPP解算精度为cm级,因而该结论还有待论证。上述研究主要利用不同海潮模型进行对比分析,而在当前GPS观测精度下,有必要分析不同地球模型对海潮负荷位移参数的影响。
本文使用静态方法,利用新西兰南北岛陆地范围内189个GPS测站连续11 a(2008~2018年)的观测数据解算8个主要潮波的位移参数,并选取7种全球海潮模型与GPS反演结果进行对比,分析4种地球模型对海潮负荷位移参数的影响,最后对GPS实测结果和模型值之间的残差进行初步探讨。
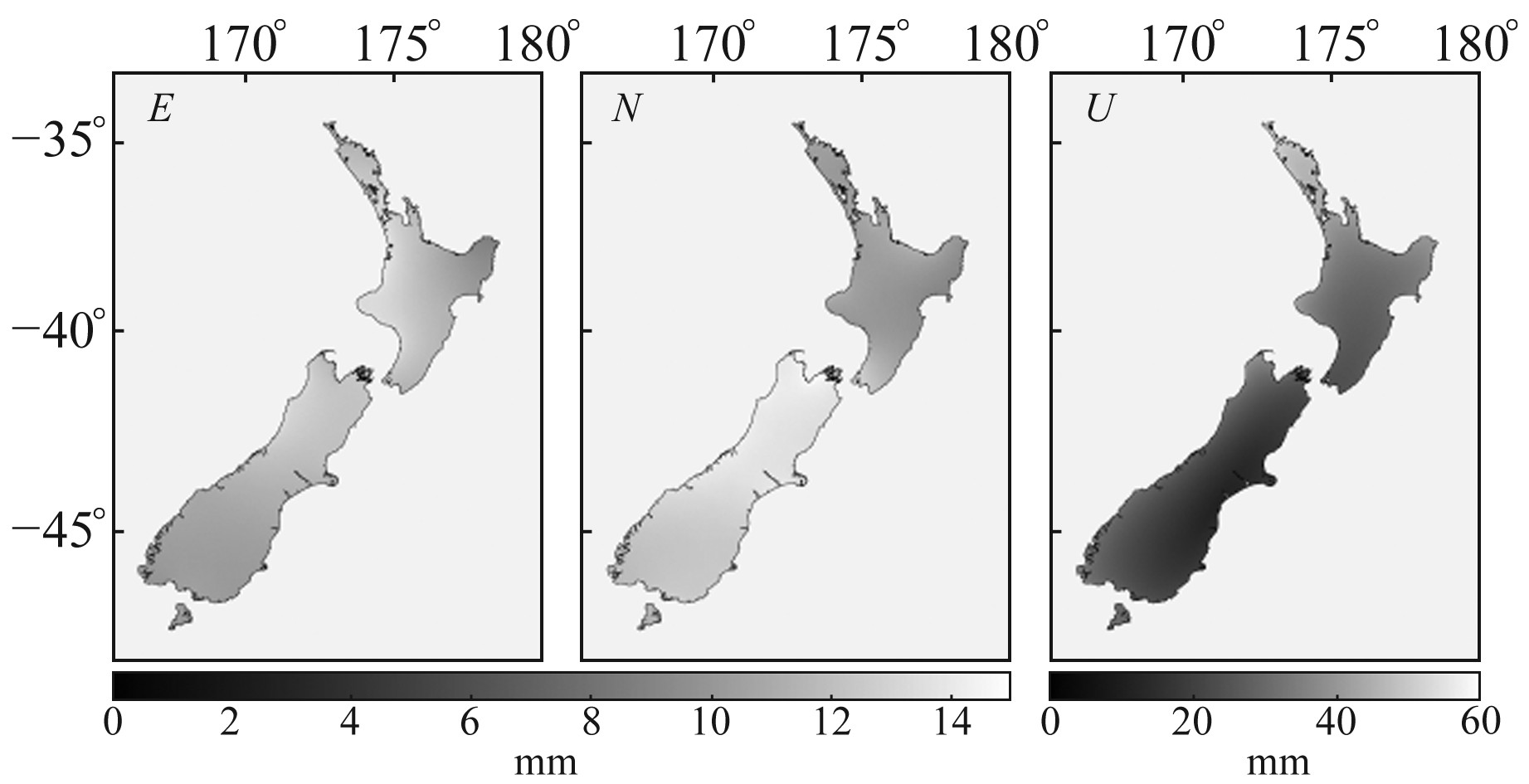
1 研究区域新西兰地处南半球中纬度地区,位于太平洋和印度-澳大利亚板块的交界处,其四周海域宽广、潮汐负荷效应明显,是全球范围内海潮负荷位移较大的区域之一。图 1为研究范围内陆地部分8个主要潮波(M2、S2、N2、K2、K1、O1、P1和Q1)海潮负荷位移的叠加,由于不同潮波不可能同时处于最大值,因此实际最大振幅小于此结果。由图可知,在垂直方向上,新西兰北岛北部区域由海潮负荷引起的形变超过50 mm, 南岛东部海潮负荷位移值仅10 mm, 海潮负荷位移南北差异明显;水平方向负荷位移较小,最大值理论上不超过15 mm。
|
图 1 新西兰地区海潮负荷位移 Fig. 1 The ocean tidal loading (OTL) displacement in New Zealand |
根据IERS2010规范[3], 并考虑周期为18.6 a的节点调制影响,测站的海潮负荷瞬时位移公式可表示为:
| $\Delta c_{k}=\sum\limits_{j=1}^{11} f_{j} A_{k, j} \cos \left(\omega_{j} t+\chi_{j}+\mu_{j}-\varphi_{k, j}\right)$ | (1) |
式中,k为站心地平坐标系中的东、北及垂直方向,j为11个潮波(4个半日潮波M2、S2、N2和K2, 4个周日潮波K1、O1、P1、Q1以及3个长周期潮波Mf、Mm、Saa), Ak, j和φk, j分别为潮波分量j在k方向上的振幅和格林尼治相位,ωj和χj分别为潮波分量j的角频率和天文幅角初相,fj和μj分别为振幅和相位的节点调制改正。本文主要考虑8个周日潮波和半日潮波,将式(1)线性化后得到:
| $\begin{aligned} \Delta c_{k}=& \sum\limits_{j=1}^{8}\left[A_{c k, j} \cos \left(\omega_{j} t+\chi_{j}\right)+\right.\\ & \left.A_{s k, j} \sin \left(\omega_{j} t+\chi_{j}\right)\right] \end{aligned}$ | (2) |
其中,
| $A_{c k, j}=f_{j} A_{k, j} \cos \left(\varphi_{k, j}-\mu_{j}\right) \\ A_{sk, j}=f_{j} A_{k, j} \sin \left(\varphi_{k, j}-\mu_{j}\right)$ |
式中,Ack, j和Ask, j分别为8个潮波3个方向上的正弦系数及余弦系数。将48个潮波参数均当作未知数,与测站坐标等参数一并求解。
2.2 数据处理策略使用GIPSY/OASIS-Ⅱ软件(版本6.4)进行静态PPP解算[4]。为与JPL精密卫星轨道、精密钟差产品的框架保持一致,采用FES2004全球海潮模型[5]计算各测站点在整体地球(包括固体地球、海洋及大气等)质心为原点框架下的海潮负荷位移和相位,作为海潮负荷位移参数估计先验值加入到原始GPS数据处理中。GIPSY解算过程中部分参数设置见表 1。
|
|
表 1 PPP静态解算参数设置 Tab. 1 Strategy of parameters of static PPP solutions |
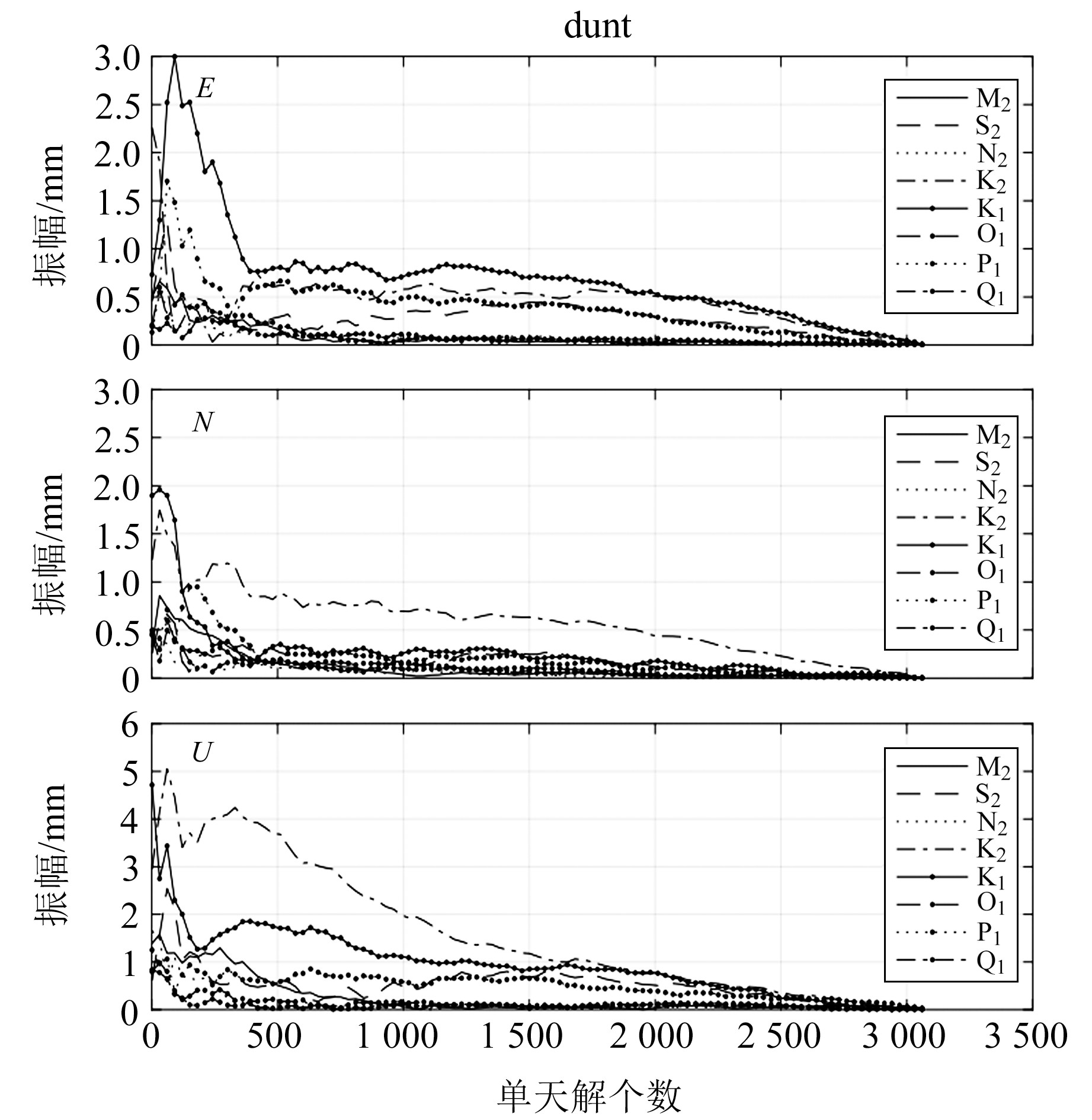
使用GIPSY解算策略求解出8个潮波单天的振幅及相位,频率相近的2个潮波之间的相关性最高可达0.8, 因此难以从单天解算结果中获取准确的振幅及相位。本文采用Yuan等[6]的方法,利用卡尔曼滤波对单天潮波参数进行融合。图 2为DUNT站的潮波参数随融合天数增加而收敛情况,当融合天数超过1 000 d时,8个潮波振幅稳定收敛,本文189个GPS测站解算天数均超过1 000 d。
|
图 2 DUNT站潮波参数收敛性 Fig. 2 Tidal estimation convergence at DUNT station |
海水质量、大气、陆地水及冰川等的影响会导致地球整体质量中心(CM)相对于固体地球质量中心(CE)产生周期性运动,因此在海潮负荷研究中有必要进行地心运动改正。本文根据Yuan等[6]计算的8个潮波的地心运动改正参数,将所有GPS解算结果及模型计算结果统一至CE框架下。
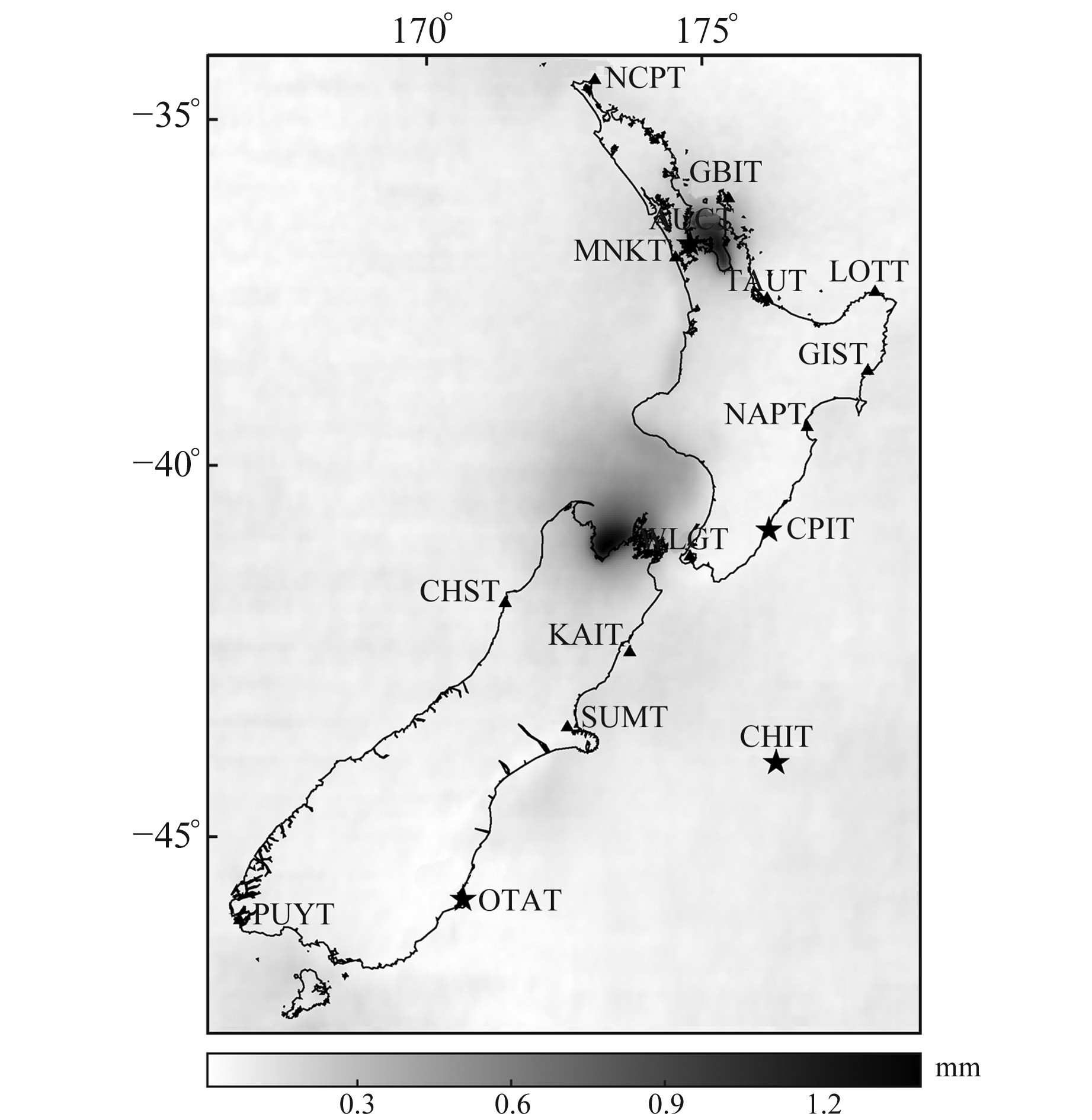
3 结果分析 3.1 不同海潮模型差异分析为验证全球海潮模型在研究区域内的误差分布情况,以M2潮波为例,选取16个验潮站2012~2019年的实测数据,根据调和分析原理提取出M2潮波的潮高,并与全球海潮模型值进行比较(所有模型均采用双线性插值至0.125°格网), 部分结果见表 2(单位m)。此外,基于PREM地球模型确定格林函数和7种全球海潮模型[7], 利用SPOTL软件计算研究区域内M2潮波垂直方向的负荷位移(空间分辨率为0.1°), 以此来分析不同全球海潮模型计算的负荷位移改正的差异性。图 3为选定区域中7种全球海潮模型确定的M2潮波负荷位移改正值的标准差,图中黑色五角星为表 2中的验潮站,黑色三角形为其他验潮站的分布情况。
北岛北部奥克兰地区7种海潮模型确定的M2潮波负荷位移改正的标准差最大可达1.1 mm, 南、北岛之间塔斯曼湾M2潮波负荷位移改正标准差可达1.5 mm。在验潮站AUCT, 不同海潮模型之间潮高差异较大,且与验潮站实测数据相差也较大,这说明在奥克兰地区海潮负荷位移标准差较大,因此在海岸复杂地区全球海潮模型尚待进一步精化。除奥克兰和塔斯曼湾地区,其他地区(如验潮站OTAT附近)不同模型RMS低于0.3 mm, 且海潮模型值与验潮站潮高实测结果吻合较好,说明海潮模型在这些地区建模精度较高。
|
|
表 2 M2潮波潮高统计 Tab. 2 The tide amplitude of M2constituent |
|
图 3 M2潮波负荷位移垂直分量标准差及验潮站分布 Fig. 3 Standard deviation of the vertical M2 OTL displacement and the locations of the tide gauges |
为评定不同海潮模型在新西兰地区的建模精度,利用SPOTL软件,选取PREM地球模型推导的格林函数(LGF)和7种全球海潮模型计算CE框架下各GPS站点处的潮波参数,并求取GPS测定的位移参数与海潮模型改正值之间的均方根误差(RMS)[6]。对于8个主要潮波分量j、坐标分量k, 所有测站(N=189)的GPS测定的位移参数值与模型改正值之间的RMS计算公式为:
| $\mathrm{RMS}_{j, k}=\left(\frac{1}{N} \sum\limits_{n=1}^{N}\left|Z_{j, k, n}\right|^{2}\right)^{1 / 2}$ | (3) |
其中,
| $Z_{j, k, n}=A_{\mathrm{GPS}}\left(\cos \varphi_{\mathrm{GPS}}+\mathrm{i} \sin \varphi_{\mathrm{GPS}}\right)_{j, k, n}- \\ A_{\text {model }}\left(\cos \varphi_{\text {model }}+\mathrm{i} \sin \varphi_{\text {model }}\right)_{j, k, n}$ | (4) |
式中,A为振幅,φ为格林尼治相位。
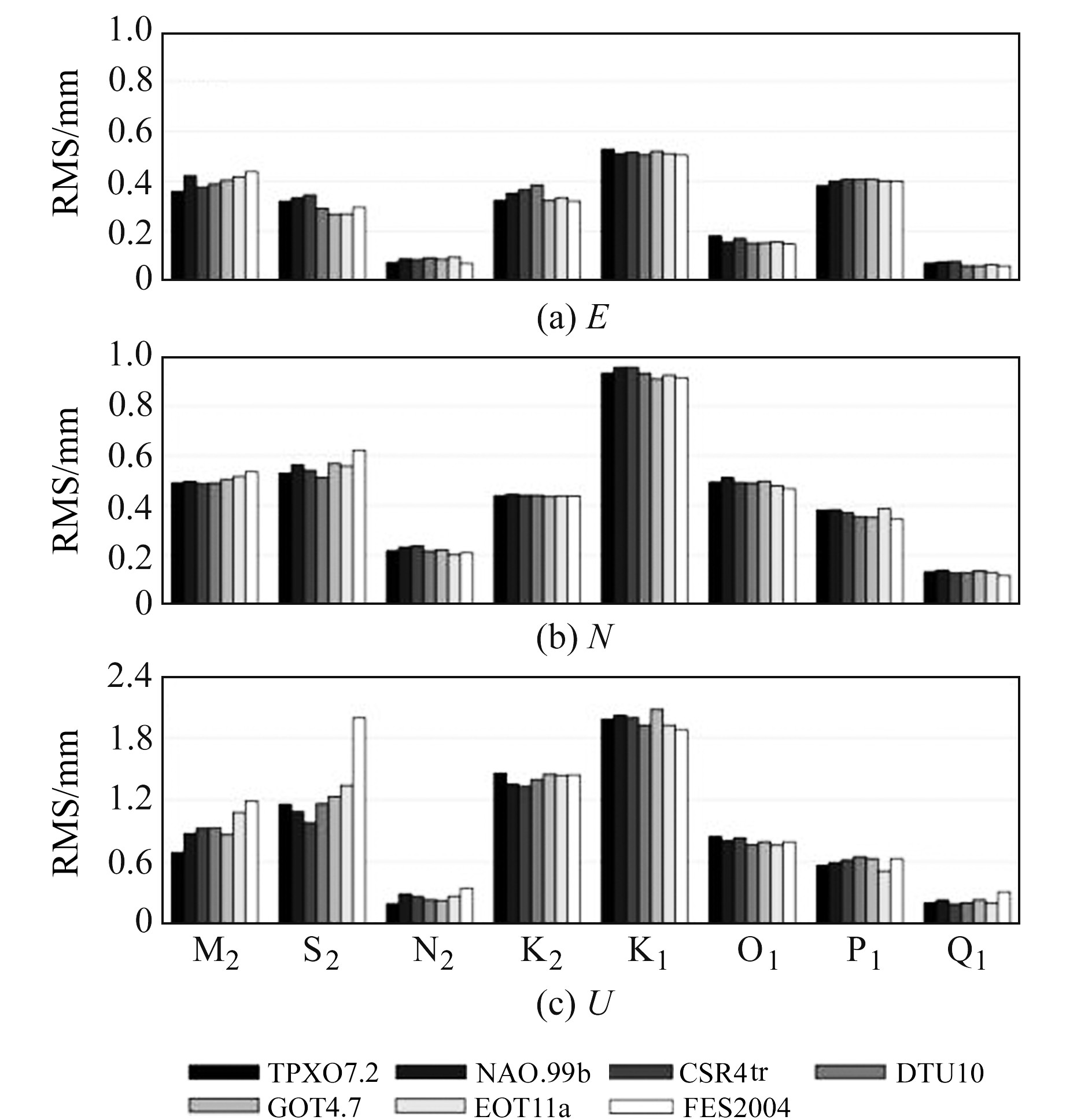
图 4给出了GPS测定参数与7种全球海潮模型改正值的RMS。可以看出,水平方向上,所有潮波参数RMS均小于1 mm, N2、Q1潮波GPS测定的位移参数值与模型值RMS仅0.1 mm, 不同海潮模型之间的RMS无显著区别;垂直方向上,S2、K2和K1潮波的RMS显著大于其他潮波,由于K2潮波周期与卫星星座周期一致,GPS轨道周期与K1潮波周期相近,因此卫星轨道误差和多路径效应可能分别是导致K1和K2潮波GPS测定的海潮负荷位移参数与模型改正值差异较大的直接原因[6]。
FES2004海潮模型在M2、S2潮波垂直方向上RMS值最大,原因可能是其吸收的测高卫星数据在复杂海岸线精度较低且未考虑地心运动改正[5]。同时由表 2可知,其M2潮高模型值与验潮站实测结果差异最大。对于M2潮波,验潮站实测潮高与GPS实测位移参数均显示,FES2004和EOT11a海潮模型不适用于新西兰地区。TPXO7.2海潮模型在新西兰地区精度最高,其中4个月球相关潮波(M2、N2、O1和Q1)与GPS测定海潮负荷位移参数的RMS值在水平方向小于0.5 mm, 垂直方向小于0.7 mm。
|
图 4 GPS海潮负荷位移估值与不同海潮模型预测之间的RMS Fig. 4 RMS of the GPS OTL displacement estimates against predictions derived by different ocean-tide models |
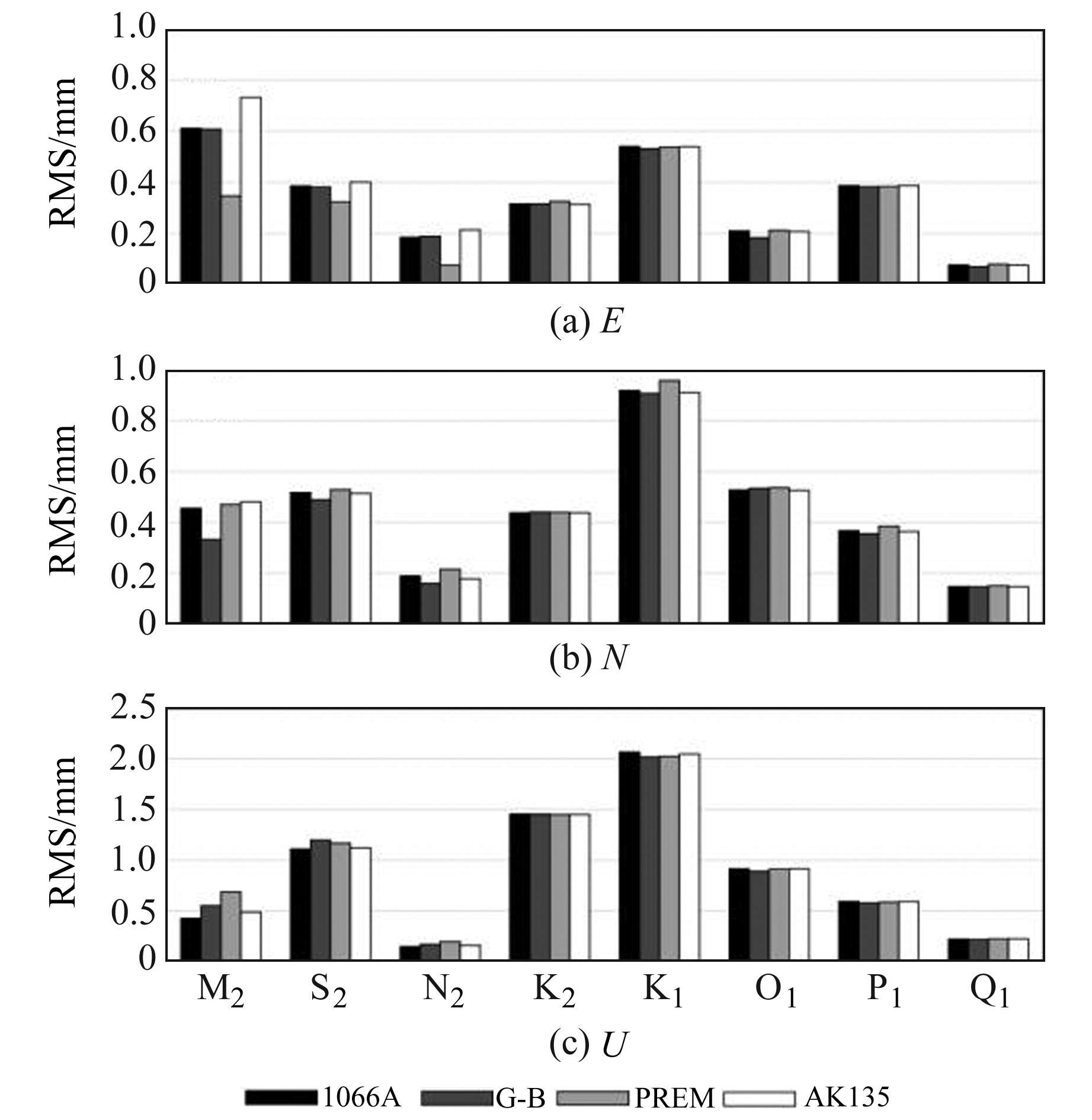
为研究不同地球模型对海潮负荷位移建模的影响,使用4种具有球对称、非自转、完全弹性和各向同性(SNREI)性质的地球模型(PREM地球模型、AK135地球模型、Gutenberg-Bullen地球模型和1066A地球模型)计算的LGF与TPXO7.2海潮模型进行离散褶积积分,利用SPOTL软件计算189个GPS测站点处的海潮负荷位移参数[8], 并利用式(3)计算RMS。
图 5显示,除M2、N2潮波外,其余6种潮波对于不同LGF与TPXO7.2海潮模型组合的计算结果差异不大,地球模型对此6种潮波负荷位移影响并不敏感,目前难以利用GPS实测值进行有效区分。M2、N2潮波RMS值分布的相似性可能是由于M2潮波与N2潮波的负荷位移特征相似且振幅呈一定比例所致。Yuan等[6]指出,不同地球模型在M2潮波三维方向上RMS值大小顺序不一致,可能是由于固体潮模型误差所致。
|
图 5 GPS海潮负荷位移估值与不同地球模型预测值之间的RMS Fig. 5 RMS of the GPS OTL displacement estimates against predictions derived by different earth models |
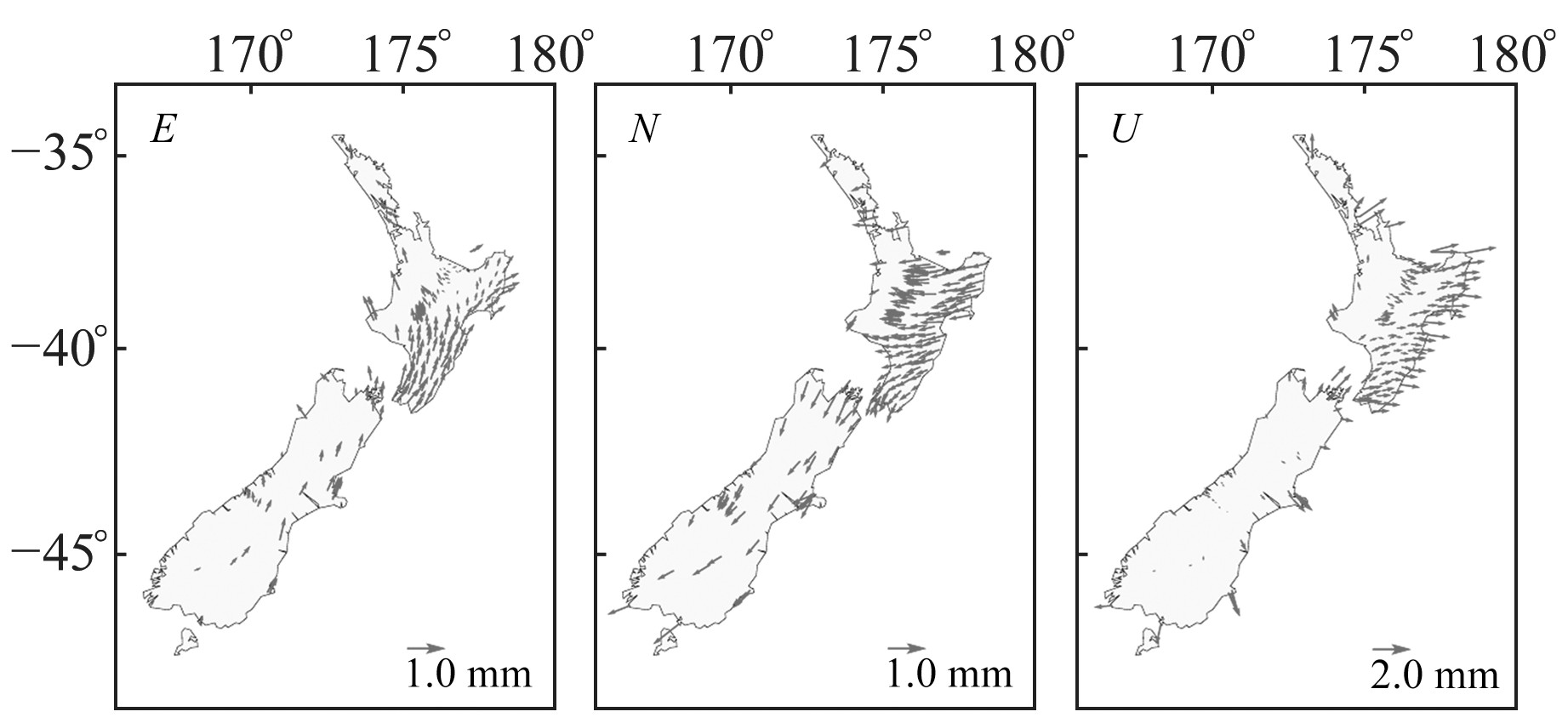
不同海潮模型和地球模型均在M2潮波差异最为明显。以M2潮波为例,选取TPXO7.2全球海潮模型和PREM地球模型获取GPS测站处海潮负荷位移改正值,并与GPS测定的位移参数求取矢量差,结果见图 6。由图可见,水平方向残差呈现出明显的区域一致性。Yuan等[6]指出,依据IERS2010使用的固体潮模型不确定性在1 mm左右,与本文残差大小基本一致。垂直方向上,沿海地区的部分站点残差显著大于内陆地区测站残差。Bos等[9]指出,采用不同的数值计算方法、海水密度和海岸线格网精化方法对海潮负荷位移的影响在0.5 mm左右,因此海潮模型误差仍是沿海地区残差的主要组成部分。
北岛奥克兰地区和南岛达尼丁地区(验潮站OTAT附近,图 3)垂直方向上的残差分别达到1.8 mm和1.4 mm, 7种海潮模型标准差在奥克兰和达尼丁区域分别约为1.0 mm和0.2 mm(图 3), 本文解算的M2潮波垂直方向GPS中误差小于0.3 mm, 因此推测,前者残差主要来源于海潮模型误差。而海潮模型误差及GPS测定的位移参数误差之和不足以完全解释验潮站OTAT周围GPS站点处的海潮负荷位移残差,因此该残差可能反映出当前使用的地球模型还存在缺陷[9]。本文所采用的PREM地球模型是SNREI地球模型,其未考虑真实地球结构的地幔滞弹性和散耗效应等特征,因此由PREM地球模型推导的负荷格林函数很大程度上将导致海潮负荷位移计算出现偏差[9]。
|
图 6 M2潮波的海潮负荷位移残差在东、北和垂直方向上的矢量分布 Fig. 6 Spatial distribution of phasor vector of OTL residuals for the M2 constituent at E, N, and U component |
本文采用新西兰地区189个连续运行观测站11 a的观测数据,基于GPS静态PPP方法精确测定了新西兰地区的海潮负荷位移,将GPS测定潮波参数与模型进行比较后得到以下结论:
1) 验潮站实测值与GPS潮波位移参数实测值均反映出TPXO7.2模型在新西兰地区建模精度最高,半日潮波的GPS测定结果与海潮模型值之间的RMS在三维方向上小于1 mm。
2) 不同地球模型之间的差异主要体现在M2、N2潮波,其余6种潮波负荷位移对不同地球模型的选取不敏感。
3) 海潮模型在部分复杂海岸区域负荷位移误差较大。部分站点异常的残差值可能反映出本文采用的SNREI地球模型存在缺陷。
本文GPS静态解算结果可用于新西兰沿海区域海潮负荷位移改正以及对地球模型的参数进行约束,如考虑软流圈弹性散耗效应等。
| [1] |
吴志露, 刘焱雄, 何秀凤, 等. 基于近岸海岛GPS数据反演海洋分潮负荷影响[J]. 地球物理学报, 2017, 60(1): 61-69 (Wu Zhilu, Liu Yanxiong, He Xiufeng, et al. Inversion of Ocean Tidal Loadings of Marine Constituents Based on the GPS Measurements in the Offshore Islands[J]. Chinese Journal of Geophysics, 2017, 60(1): 61-69)
(  0) 0) |
| [2] |
魏国光, 王琪洁, 彭葳, 等. 利用短期静态PPP结果反演海潮负荷位移[J]. 大地测量与地球动力学, 2019, 39(6): 607-612 (Wei Guoguang, Wang Qijie, Peng Wei, et al. Using Short Time-Scale Static PPP Results to Invert Ocean Tide Loading Displacement[J]. Journal of Geodesy and Geodynamics, 2019, 39(6): 607-612)
(  0) 0) |
| [3] |
Petit G, Luzum B. IERS Technical Note No. 36, IERS Conventions(2010)[Z]. International Earth Rotation and Reference Systems Service, Frankfurt, 2010
(  0) 0) |
| [4] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5 005-5 017 DOI:10.1029/96JB03860
(  0) 0) |
| [5] |
Lyard F, Lefevre F, Letellier T, et al. Modelling the Global Ocean Tides: Modern Insights from FES2004[J]. Ocean Dynamics, 2006, 56(5-6): 394-415 DOI:10.1007/s10236-006-0086-x
(  0) 0) |
| [6] |
Yuan L G, Chao B F, Ding X L, et al. The Tidal Displacement Field at Earth's Surface Determined Using Global GPS Observations[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(5): 2 618-2 632 DOI:10.1002/jgrb.50159
(  0) 0) |
| [7] |
Dziewonski A M, Anderson D L. Preliminary Reference Earth Model[J]. Physics of the Earth and Planetary Interiors, 1981, 25(4): 297-356 DOI:10.1016/0031-9201(81)90046-7
(  0) 0) |
| [8] |
Agnew D C. NLOADF: A Program for Computing Ocean-Tide Loading[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5 109-5 110 DOI:10.1029/96JB03458
(  0) 0) |
| [9] |
Bos M S, Penna N T, Baker T F, et al. Ocean Tide Loading Displacements in Western Europe: 2. GPS-Observed Anelastic Dispersion in the Asthenosphere[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(9): 6 540-6 557 DOI:10.1002/2015JB011884
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


