Besl等[1]提出的迭代最近点(iterative closest point, ICP)算法是目前最经典的点云精配准算法,但此算法对点云初始位置要求高,否则容易陷入局部最优,且存在收敛速度较慢的问题[2]。许多学者对该算法进行了改进和创新,提出了一些新的算法[3-4]。Rusu等[5]提出一种依据点云的快速点特征直方图(fast point feature histogram, FPFH)特征,并使用采样一致性初始配准(sample consensus intial alignment, SAC-IA)的方法,该方法虽然显著提高了配准精度,但降低了配准效率,常用来进行初始配准。正态分布变换(normal distribution transformation, NDT)算法[6]不依据对应点的特征进行匹配,而是通过最优化技术确定点云之间的最佳匹配。与ICP算法相比,NDT算法在配准海量点云数据时速度较快、精度较高[7], 但仍需要较好的初始位置,因此需要对点云进行初始配准,以提高配准的精度和效率。
基于以上研究,本文提出一种融合SAC-IA和NDT的点云配准方法,并通过实验对该方法的配准精度和效率进行验证。
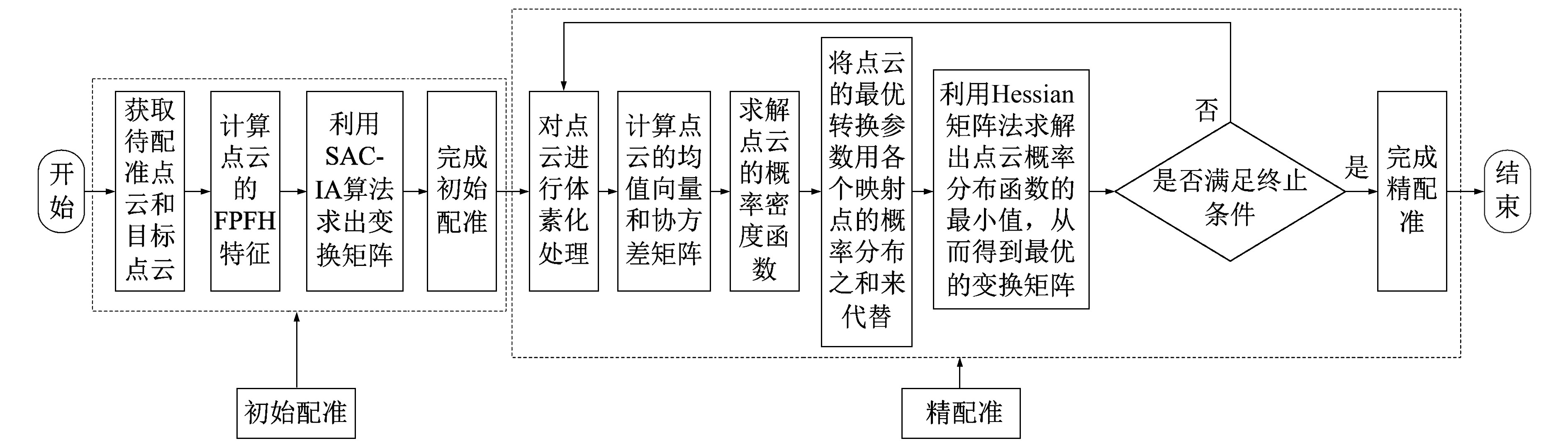
1 点云配准流程本文提出的点云配准方法流程见图 1。首先计算待配准点云和目标点云的FPFH特征,并依据二者相似的FPFH特征,利用SAC-IA算法求出变换矩阵,从而完成初始配准;在此基础上,对点云进行体素化处理,求得点云的均值向量和协方差矩阵,并求出点云的概率密度函数;接着将点云的最优转换参数用各个映射点的概率分布之和来代替;然后利用Hessian矩阵法求出点云概率分布函数的最小值,进而得到最优变换矩阵;最后判断是否满足终止条件,完成点云的精配准。
|
图 1 点云配准流程 Fig. 1 Process of point cloud registration |
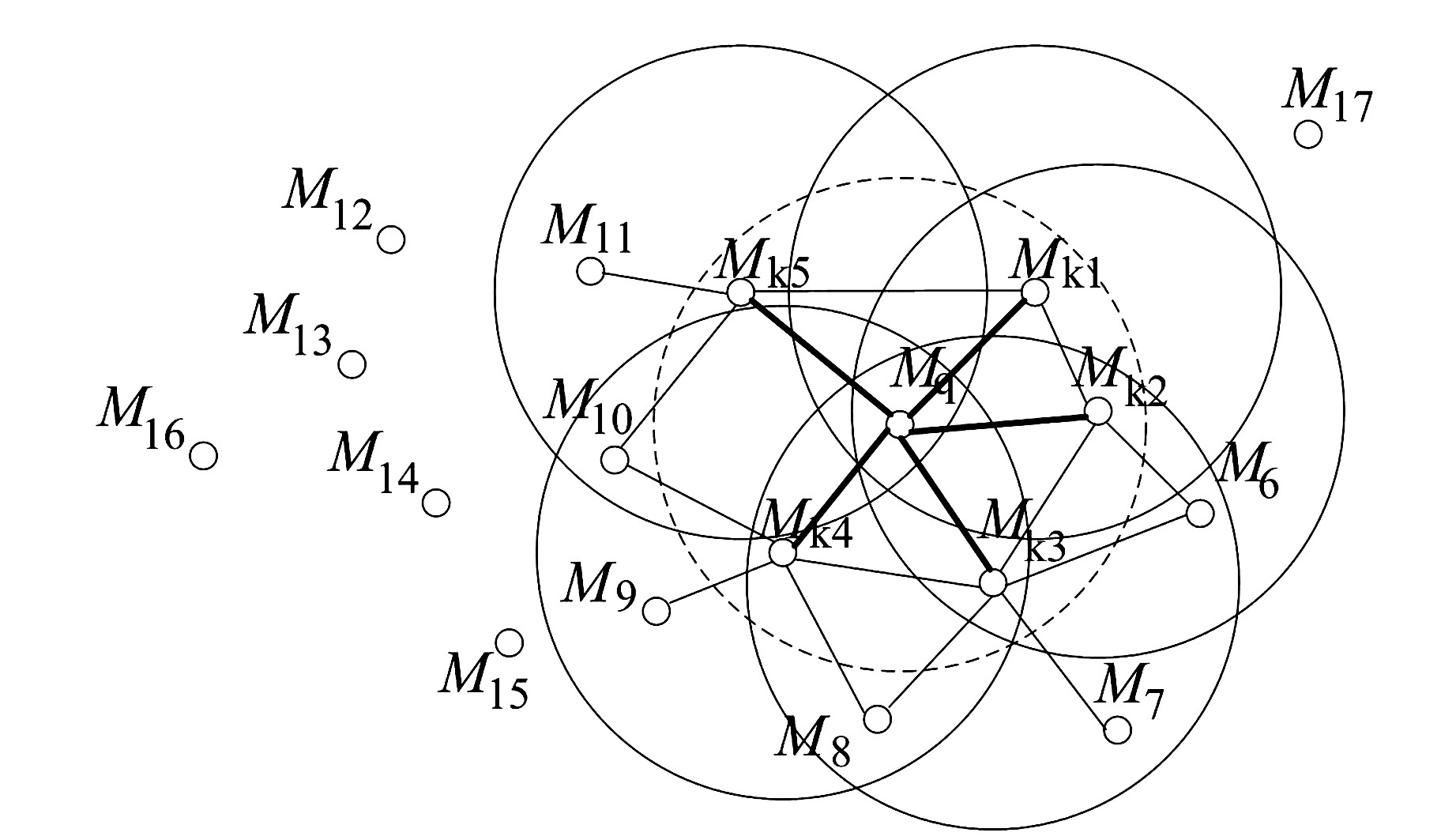
FPFH算法基于局部特征描述,是通过对点特征直方图(point feature histograms, PFH)[8]改进得到的。PFH将查询点与邻域点之间的空间差异进行参数化处理,形成一个对点的k邻域几何属性进行描述的多维直方图。关于PFH的详细介绍可参考文献[8]。与PFH相比,FPFH由于没有计算全互联Mq的所有邻近点,因而降低了算法的计算量,把复杂度由O(k2)降低到O(k), FPFH的计算原理见图 2。
|
图 2 FPFH计算原理 Fig. 2 Calculation principle of FPFH |
计算FPFH特征描述子的步骤如下。
1) 计算出每个待计算点Mq与其所有邻域点之间的相对关系,从而建立简化的点特征直方图(simplified point feature histogram, SPFH), 并记为S(Mq)。
2) 根据步骤1)计算得到的k个邻域点的SPFH特征计算FPFH特征,记为F(Mq), 表示为:
| $F\left(M_{q}\right)=S\left(M_{q}\right)+\frac{1}{k} \sum\limits_{i=1}^{k} \omega_{i} \cdot S\left(M_{q}\right)$ | (1) |
式中,ωi为第i个邻域点SPFH特征的加权值,
针对经典ICP算法配准易陷入局部最优的问题,本文在初始配准阶段使用SAC-IA算法,其算法步骤如下。
1) 对采样点进行选取。在待配准点云M中选取n个采样点,并且要满足采样点两两之间的距离大于预先设定的最小距离阈值d, 用以保证各采样点的FPFH特征均不相同。
2) 对采样点的对应点进行查找。依据采样点的FPFH特征,在目标点云N中通过近邻搜索找到与采样点中每个点FPFH相差最小的点,即为特征相似的点,将其作为目标点云N中与待配准点云M中的采样点相对应的点,并通过RANSAC算法剔除错误的对应点对,从而保证相似特征点对的正确匹配。
3) 求解变换关系。首先求出对应点之间的变换矩阵,然后依据该变换计算对应点变换后的距离误差和函数,并将此函数作为评判配准性能的指标。此处多使用Huber罚函数来表示距离误差和函数,记为
| $H\left(l_{i}\right)=\left\{\begin{array}{l}\frac{1}{2} l_{i}^{2}, \left\|l_{i}\right\|<m_{l} \\ \frac{1}{2} m_{l}\left(2\left\|l_{i}\right\|-m_{l}\right), \left\|l_{i}\right\|>m_{l}\end{array}\right.$ | (2) |
式中,ml为预先设定的值,li为第i组对应点经过变换之后的距离差。最后为了使误差函数取得最小值,需要从所有的变换中找出一组最优的变换,从而进行初始配准。
3 基于NDT的精配准SAC-IA初始配准让待配准的两片点云位置尽可能地靠近,缩小点云之间的旋转和平移误差,使得源点云和目标点云具有较好的初始位置。为了进一步缩小偏差,在初始配准的基础上进行NDT配准以提高配准的精度,从而使精配准后的结果达到预设的约束条件。NDT是把三维点云分成大小均匀的立方体,并把立方体中的点云数据转换成概率密度函数,然后依据矩阵法求出转换关系。相对于ICP算法,该方法不需要每次迭代都重新匹配对应点对,因此配准效率较高。其算法步骤如下。
1) 把点云模型划分为均匀大小的立方体。
2) 求出各个立方体中点的均值向量q和协方差矩阵C:
| $\boldsymbol{q}=\frac{1}{n} \sum\limits_{k=1}^{n} \boldsymbol{x}_{k}$ | (3) |
| $\boldsymbol{C}=\frac{1}{n-1} \sum\limits_{k=1}^{n}\left(\boldsymbol{x}_{k}-\boldsymbol{q}\right)\left(\boldsymbol{x}_{k}-\boldsymbol{q}\right)^{\mathrm{T}}$ | (4) |
式中,n为立方体中点的总数,xk为立方体中的一点。
3) 对点xk进行正态分布建模N(q, C), 其中xk的概率密度函数表示为:
| $p(x)=\frac{1}{\sqrt{2 \pi|\boldsymbol{C}|}} \exp \left[-\frac{(\boldsymbol{x}-\boldsymbol{q})^{\mathrm{T}} \boldsymbol{C}^{-1}(\boldsymbol{x}-\boldsymbol{q})}{2}\right]$ | (5) |
4) 根据变换矩阵T对待配准点云的每个点进行变换,然后依据变换后的点T(xi)所在的立方体的概率密度分布函数计算相应的概率分布函数。
5) 把各个待配准点的相应概率分布相乘,并将相乘的结果作为变换矩阵T的分数值s(p):
| $s(p)=\prod\limits_{i=1}^{n}\left[\boldsymbol{T}\left(x_{i}\right)\right]$ | (6) |
6) 依据Hessian矩阵法计算s(p)的最优解,从而得出最佳变换矩阵。
4 实验结果与分析本文实验的硬件环境为Inter(R) Core(TM) i7-8750H CPU @2.20 Hz处理器,8.00 GB内存;系统环境为64位Win10操作系统;软件环境为Visual Studio2013、开源点云库PCL1.8.0。实验使用的点云模型为斯坦福大学点云库的bunny和horse。为了进一步分析该方法的普适性,用采集的点云椅子进行验证。如图 3所示为初始点云可视化结果,其中绿色点云为源点云,红色点云为目标点云。为了证明本文方法的有效性,分别使用经典ICP算法、文献[3]方法和本文方法对点云模型bunny、horse以及椅子进行配准实验,并对3者结果进行对比分析。

|
图 3 初始点云可视化 Fig. 3 Visualization of the initial point cloud |
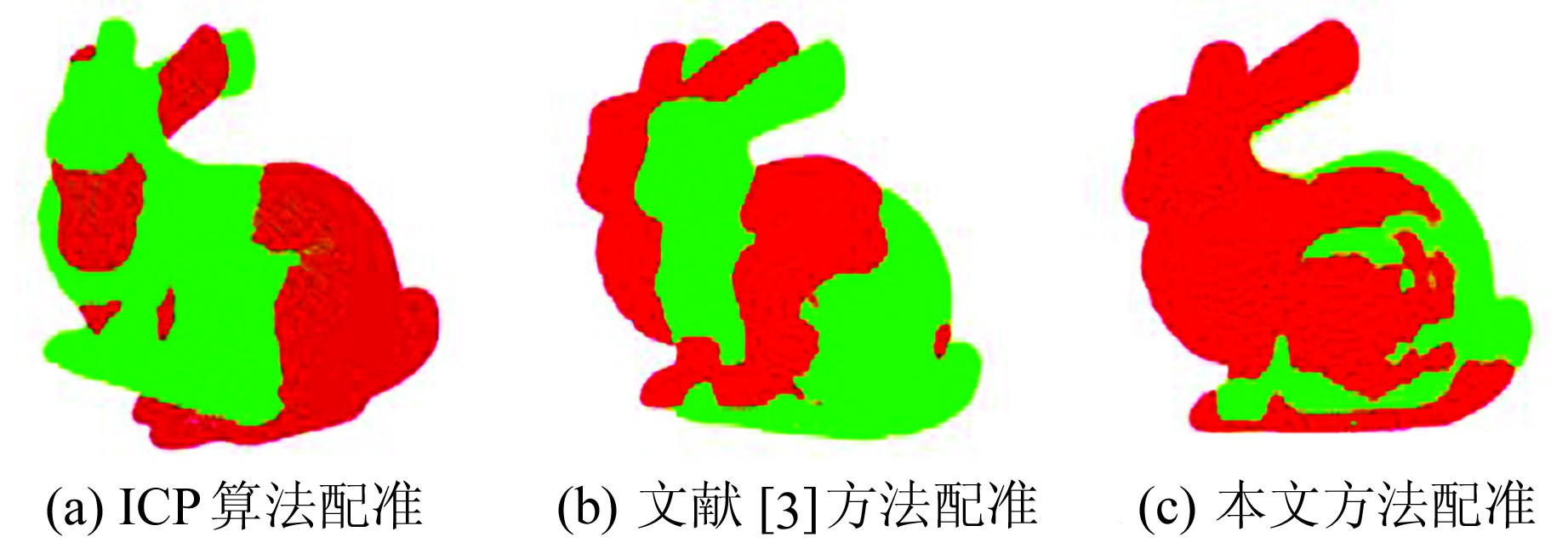
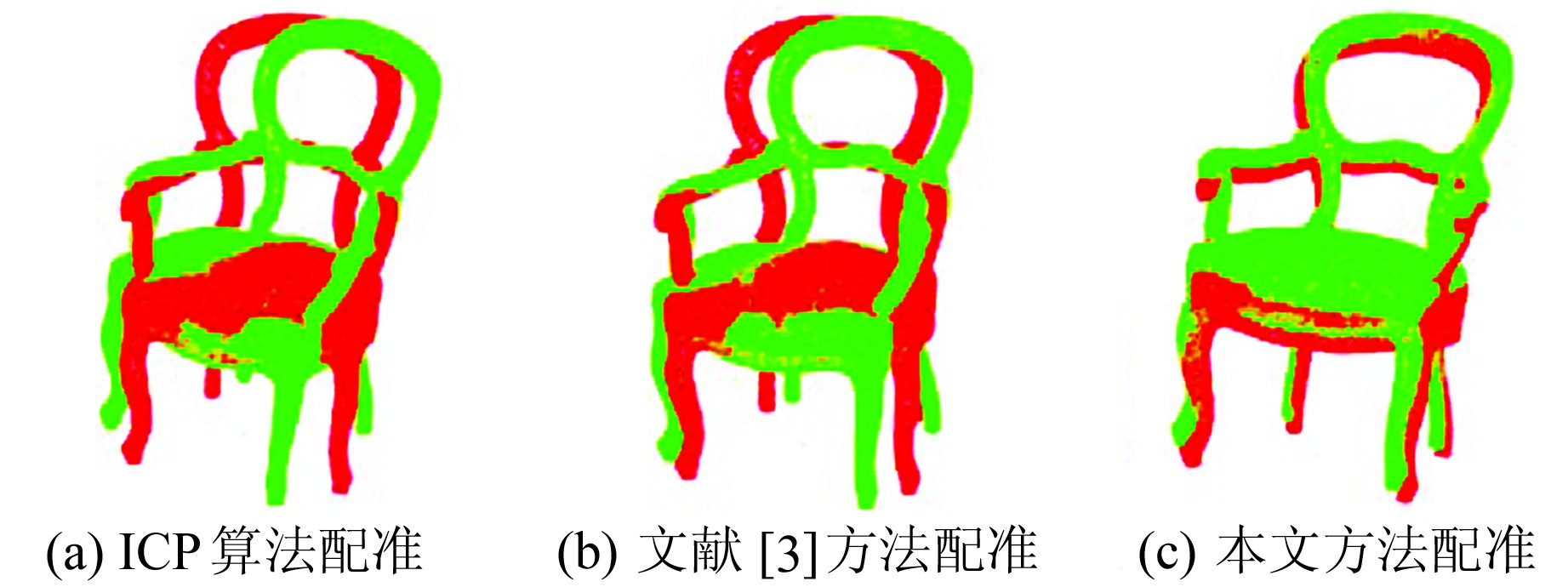
图 4~6分别为经典ICP算法、文献[3]方法和本文方法的点云bunny、horse和椅子的配准结果,图 7为点云bunny、horse和椅子使用本文方法配准时得到的刚体变换结果。
|
图 4 Bunny配准结果 Fig. 4 Registration results of bunny |

|
图 5 Horse配准结果 Fig. 5 Registration results of horse |
|
图 6 椅子配准结果 Fig. 6 Registration results of chair |

|
图 7 刚体变换结果 Fig. 7 Results of rigid transformation |
通过上述配准结果可以看出,使用ICP算法配准时,点云模型bunny和horse的头部、尾部、脚掌及耳朵等多处部位出现明显的配准偏差。对比直接使用ICP算法,本文方法在使用采样一致性算法初始配准的基础上使用正态分布变换进行精配准,可以大幅提高配准的质量,点云模型多处部位的配准结果得到有效改善。对于点云椅子而言,使用本文方法得到的配准效果也明显优于ICP算法。同时,与文献[3]方法相比,本文方法的配准结果更好。
本文实验以欧氏适合度评分作为配准误差评判指标。欧氏适合度评分表示输出点云到最近目标点云对应点对的距离平方和,距离平方和越小,说明重合度越好、配准精度越高。同时,比较配准所用的时间,以衡量配准的效率。表 1为配准用时和配准误差的统计结果。
|
|
表 1 配准结果比较 Tab. 1 Comparison of registration results |
由表 1可见,对于点云bunny、horse和椅子,本文方法的配准误差分别是ICP算法的18.9%、18.4%和18.8%, 同时配准效率也有一定的提高。与文献[3]方法相比,虽然本文方法需要消耗更长的时间,但配准精度更高,取得了更好的配准效果。
5 结语针对两片点云初始位置差距较大时使用ICP算法配准易陷入局部最优的问题,本文提出一种基于SAC-IA和NDT融合的点云配准方法。该方法首先提取点云的FPFH特征,依据FPFH特征和SAC-IA算法对点云进行初始配准,然后在此基础上使用NDT算法进行精配准。通过与ICP算法的对比实验表明,该方法的配准精度有显著提高,同时效率也有一定的提升。由于在三维重建过程中点云数据配准是十分关键的一步,配准的成功与否会对后续的重建结果造成直接影响,因此,本文的配准方法可为后期点云模型重建提供参考。但需要注意的是,初始配准时计算点云FPFH特征仍需消耗一定的时间,这是该方法日后需要优化的地方;同时,该方法中NDT配准时参数的阈值设置还需进一步优化。
| [1] |
Besl P J, McKay N D. A Method for Registration of 3-D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256
(  0) 0) |
| [2] |
Han J D, Yin P, He Y Q, et al. Enhanced ICP for the Registration of Large-Scale 3D Environment Models: An Experimental Study[J]. Sensors, 2016, 16(2): 228 DOI:10.3390/s16020228
(  0) 0) |
| [3] |
刘江, 张旭, 朱继文. 一种基于K-D树优化的ICP三维点云配准方法[J]. 测绘工程, 2016, 25(6): 15-18 (Liu Jiang, Zhang Xu, Zhu Jiwen. ICP Three-Dimensional Point Cloud Registration Based on K-D Tree Optimization[J]. Engineering of Surveying and Mapping, 2016, 25(6): 15-18)
(  0) 0) |
| [4] |
王畅, 舒勤, 杨赟秀, 等. 利用结构特征的点云快速配准算法[J]. 光学学报, 2018, 38(9): 175-182 (Wang Chang, Shu Qin, Yang Yunxiu, et al. Quick Registration Algorithm of Point Clouds Using Structure Feature[J]. Acta Optica Sinica, 2018, 38(9): 175-182)
(  0) 0) |
| [5] |
Rusu R B, Blodow N, Beetz M. Fast Point Feature Histograms(FPFH)for 3D Registration[C]. IEEE International Conference on Robotics and Automation, Kobe, 2009
(  0) 0) |
| [6] |
Biber P, Strasser W. The Normal Distributions Transform: A New Approach to Laser Scan Matching[C]. IEEE /RJS International Conference on Intelligent Robots and Systems, Las Vegas, 2003
(  0) 0) |
| [7] |
Magnusson M, Nüchter A, Lörken C, et al. Evaluation of 3D Registration Reliability and Speed——A Comparison of ICP and NDT[C]. IEEE International Conferenceon Roboticsand Automation, Kobe, 2009
(  0) 0) |
| [8] |
Rusu R B, Blodow N, Marton Z C, et al. Aligning Point Cloud Views Using Persistent Feature Histograms[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, 2008
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

