全球导航卫星系统(global navigation satellite system, GNSS)技术的不断发展为精确探究地壳运动规律开辟了途径。通过对长期观测得到的数据进行精密处理,可以测定板块运动的速度和方向,进而得到地壳运动形变规律[1-2]。连续运行参考站(continuously operating reference stations, CORS)是采集地理空间信息的重要基础设施,其能够提供连续稳定的GNSS观测数据,为研究区域三维运动状态提供重要依据。
安徽省卫星定位综合服务系统(AHCORS)建成于2011年,其包含50余个均匀分布于全省的参考站,是建设“数字安徽”的基础框架,同时也为研究安徽省地壳运动形变规律积累了数据。安徽省地处我国华东地区,郯庐断裂带将其一分为二,以东属于下扬子断块,以西属于华北断块。后者南部的大别山区属于秦岭-大别山断块,该区域地质构造较为复杂,是地震活跃地区[3-4], 对该区域的地壳运动状态进行研究具有重要意义。袁鹏等[5]获取了AHCORS 2011-11~2012-09的数据,首次定量分析安徽省地壳运动状态,并揭示华北平原的地面沉降状况。本文在前人研究的基础上,解算AHCORS 2013-01~2018-06期间的观测数据,得到安徽省CORS在ITRF2008框架下的坐标时间序列;通过模型拟合得到噪声序列,并计算噪声序列的谱指数,从而确定安徽省CORS的最优噪声模型;同时,顾及有色噪声的影响,解算AHCORS在ITRF2008框架下的水平速度场和垂直速度场,并给出其相对于欧亚板块的运动状态。
1 GNSS数据处理 1.1 数据处理采用GAMIT/GLOBK软件对AHCORS 19个测站2013-01~2018-06的观测数据进行解算。为了提高数据解算的精度,同时解算我国及周边地区5个IGS站(CHAN、DAEJ、URUM、TCMS、LHAZ)的同期观测数据。数据处理主要分为2个部分:1)运用GAMIT进行基线解算,得到AHCORS和IGS测站的松弛单日解;2)通过GLOBK进行滤波平差,同时引入由SOPAC处理分析的全球子网IGS1-7解算,进而得到AHCORS在ITRF2008框架下的坐标时间序列。
单日解解算时,主要策略包括:1)采用双差相位解算方法;2)同时解算卫星轨道和测站坐标;3)对流层延迟改正采用维也纳映射函数(Vienna mapping function 1, VMF1), 每2 h估计1个天顶湿延迟参数;4)海潮改正采用有限元解2004(finite element solutions 2004, FES2004)网格模型;5)使用IGS精密星历和地球自转参数,并给予适当约束,对极移和极移速率分别给予3″/d、0.3″/d的约束,对UT1变化和UT1变化速率分别给予0.2″/d和0.02″/d的约束;6)选择我国及周边地区的5个IGS站作为基准站,解算时IGS站点的3个坐标分量均给予0.05 m的约束。
运用GLOBK获取测站坐标时间序列时,主要解算方案为:1)为了进行全球网平差,引入由SOPAC处理分析的全球子网IGS1-7。在平差解算时将AHCORS单日松弛解与IGS1-7松弛解合并,并将解方案中协方差矩阵的相对权重因子取1.0;2)利用GLOBK综合各网单日解,并以IGS站在ITRF2008框架下的坐标和速度为基准,解算AHCORS的坐标时间序列。
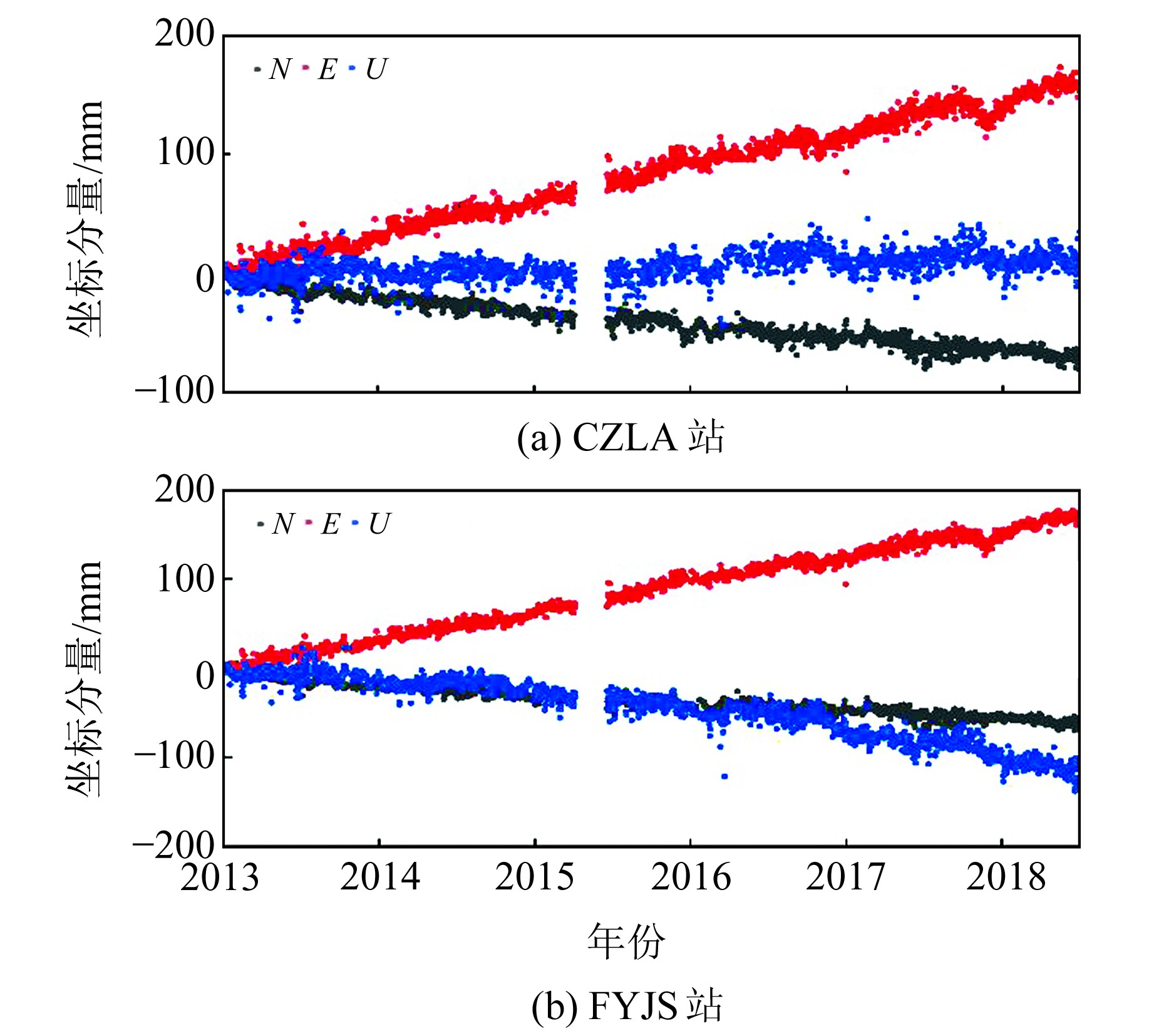
图 1给出了滁州来安(CZLA)站和阜阳界首(FYJS)站的坐标时间序列图,其中2015-02~04由于设备原因出现数据缺失。由图可见,CZLA站和FYJS站的东分量和北分量均具有较为明显的线性趋势,相比之下,CZLA站高程方向的运动趋势不如FYJS站的明显,后者垂直分量上出现非常明显的下降趋势。
|
图 1 CZLA站和FYJS站坐标时间序列 Fig. 1 Coordinate time series of CZLA and FYJS stations |
GNSS坐标时间序列一般根据如下模型进行拟合,以便更好地研究其线性项、周期项和噪声项:
| $y\left(t_{i}\right)=a+b t_{i}+c \sin \left(2 \mathrm{\pi} t_{i}\right)+d \cos \left(2 \mathrm{\pi} t_{i}\right)+ \\ e \sin \left(4 \mathrm{\pi} t_{i}\right)+f \cos \left(4 \mathrm{\pi} t_{i}\right)+ \\ \sum\limits_{j=1}^{n_{i}} g_{j} H\left(t_{i}-T_{h_{j}}\right)+\sum\limits_{j=1}^{n_{h}} h_{j} H\left(t_{i}-T_{h_{j}}\right) t_{i}+ \\ \sum\limits_{j=1}^{n_{k}} k_{j} \exp \left(-\frac{\left(t_{i}-T_{h_{j}}\right)}{\tau_{i}}\right) \times H\left(t_{i}-T_{h_{j}}\right)+v_{i}$ | (1) |
式中,ti为时间(单位年); 待定系数a为截距,b为线性速率,c和d为周年项系数,e和f为半周年项系数;gj为远场地震后产生的同震位移;hj为震后地壳运动速度的改变量;系数kj为震后变形的指数衰减;H(t)为阶跃函数;τi为松弛时间;vi为残差。根据上述参数模型对各个参数进行拟合,可以有效地估计坐标时间序列中的位置和速度信息及其季节性变化。
2 噪声分析外界环境变化(如季节性变化)使观测墩收缩膨胀、解算GNSS观测数据时引入的校正模型不正确等因素,均会导致GNSS坐标时间序列存在噪声。研究噪声之前需要按照以上模型扣除线性和非线性项,得到残差序列。在讨论噪声序列时,最初认为其中仅包含与时间无关的噪声,即白噪声,后经研究认为,其中还含有与时间相关的噪声。
噪声的幂律性质可以表示为:
| $P(f)=P_{0} f^{\alpha}$ | (2) |
式中,P(f)为噪声序列的功率谱密度;f为该类噪声对应的频率;P0和α为待定参数。将式(2)两边取对数得:
| $\ln P(f)=\ln P_{0}+\alpha \ln f$ | (3) |
由式(3)可以看出,谱指数α是功率谱密度对数与噪声频率对数分布图的斜率。谱指数为-3~1之间的实数,不同的谱指数对应的噪声不同,α=0时表示噪声类型为白噪声(white noise, WN); α=-1时噪声类型为闪烁噪声(flick noise, FN); α=-2时噪声类型为随机游走噪声(random walk noise, RWN)。除了白噪声,其余噪声均属于有色噪声。
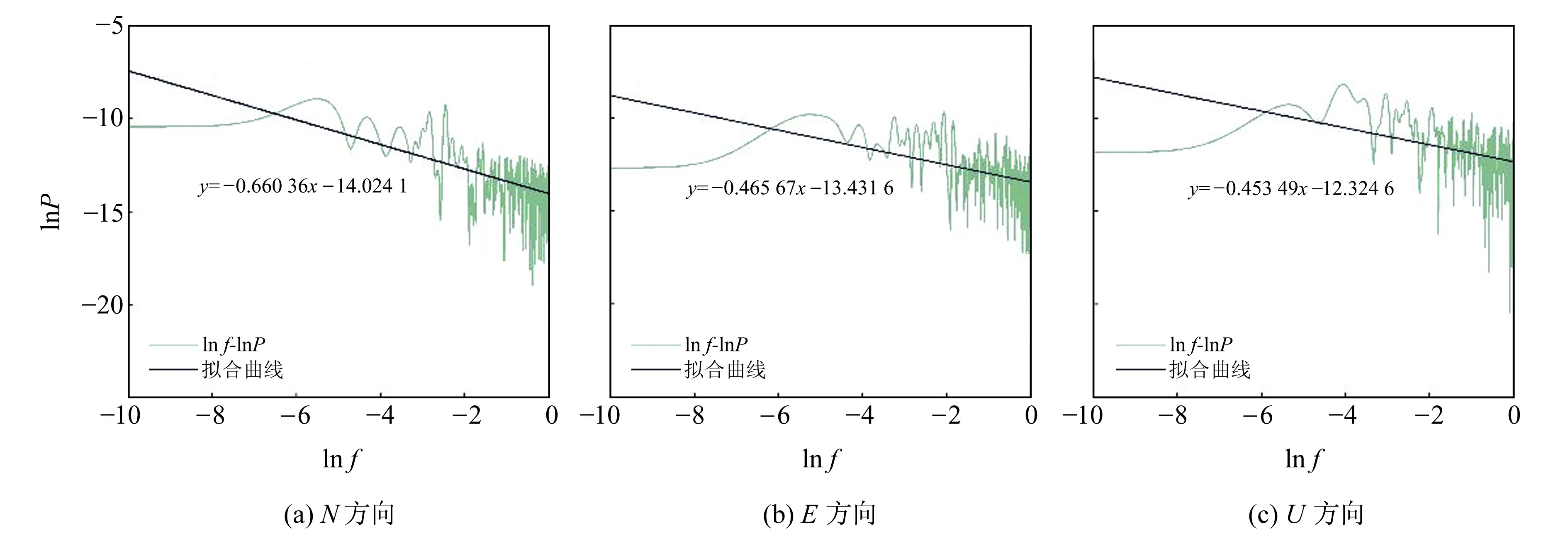
2.1 频谱分析采用周期图法求得参考站各方向噪声序列的功率谱密度,得到功率谱密度与频率的双对数图,再利用最小二乘拟合截距和斜率得到P0和α。其中CZLA站的功率谱密度与频率双对数分布图如图 2所示。经计算,19个站点的3个坐标分量的噪声谱指数均在-0.7~0之间,结合文献[6]可以判断,噪声项具有白噪声和闪烁噪声结合(WN+FN)的特点。
|
图 2 CZLA站各分量噪声序列功率谱密度与频率双对数分布 Fig. 2 The double logarithmic graphics of power spectral density and frequency noise sequence of each component of CZLA station |
GNSS坐标时间序列中含有有色噪声,仅考虑白噪声可能会低估速度估计的不确定度[7]。本文利用CATS软件[8]分别计算在白噪声(WN)和白噪声+闪烁噪(WN+FN)2种模型下的速度项并进行对比。表 1列出测站坐标时间序列各分量在不同噪声模型下的速度估计值,其中第1行为WN模型,第2行为WN+FN模型;倍数列是WN+FN模型下各分量速度估计值的精度与WN模型下的比值。由表 1可知,在分析GNSS坐标时间序列时,噪声序列中仅含有白噪声会导致速度项的精度被明显高估,且对速度值的估计产生影响。袁鹏等[5]仅采用白噪声假设得到的速度不确定度可能会过于乐观。
|
|
表 1 测站坐标时间序列各分量的速度估计值及其精度 Tab. 1 Velocity estimation and accuracy of each component of the coordinate time series of the stations |
AHCORS在ITRF2008框架下的水平速度是以地球质心为基准的地壳水平运动速度,这其中包含了欧亚板块相对于ITRF全球参考框架的运动,且一般情况下板块运动速度要比变形速度大。因此,要得到安徽省CORS的水平差异性运动,需要将其在ITRF2008框架下的水平速度场转化到相对于欧亚板块的运动速度。根据刚性块体的旋转运动模型,在地心坐标系中,如果有一个块体的绝对欧拉矢量为Ω(ωx, ωy, ωz), 在该块体上某点(λ, φ)的矢径为r(x, y, z), 其东向速度和北向速度可表示为[9]:
| $\left[\begin{array}{l}V_{E} \\ V_{N}\end{array}\right]=\left[\begin{array}{ccc}-r \cos \lambda \sin \varphi & -r \sin \lambda \sin \varphi & r \cos \varphi \\ r \sin \lambda & -r \cos \lambda & 0\end{array}\right]\left[\begin{array}{l}\omega_{x} \\ \omega_{y} \\ \omega_{z}\end{array}\right]$ | (4) |
表 2(单位mm/a)统计了安徽CORS在ITRF2008框架下的三维速度估值和中误差(在解算速度时顾及了有色噪声的影响)。由表可见,AHCORS在ITRF2008框架下的水平运动方向多为东南方向,且N、E方向的精度明显优于U方向。N方向速度最大值为-9.40 mm/a, 最小值为-15.36 mm/a, 均值为-12.27 mm/a; E方向速度最大值为31.41 mm/a, 最小值为27.59 mm/a, 均值为29.25 mm/a。参考站平均水平运动速率为31.72 mm/a, 方向为E22.76°S, 与袁鹏等[5]的研究结果一致。
|
|
表 2 AHCORS在ITRF2008框架下三维速度及其中误差统计 Tab. 2 Statistics of velocity and root mean square error of three dimension of AHCORSunder ITRF2008 frame |
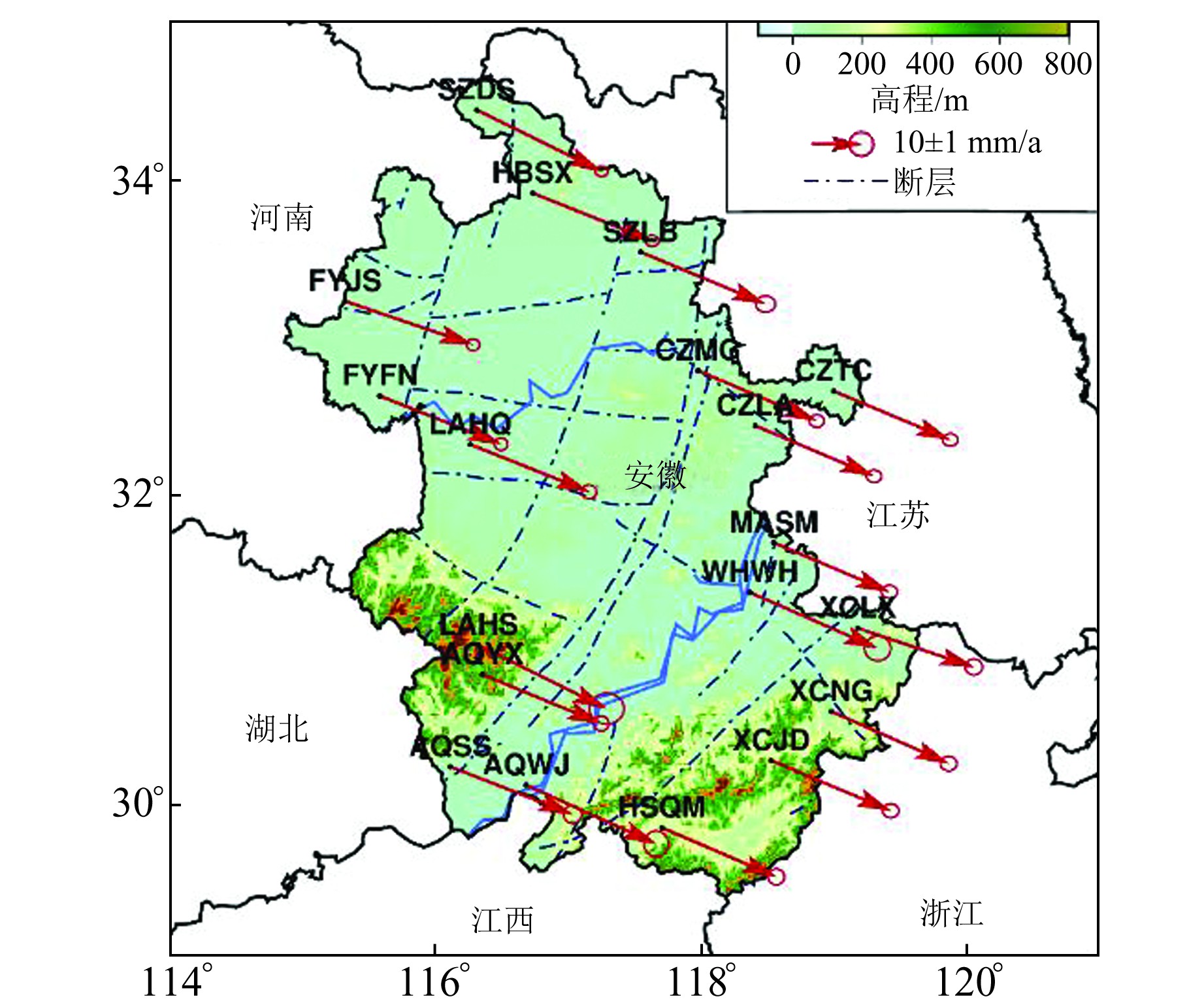
图 3表示AHCORS在ITRF2008框架下的速度场,其中蓝色虚线为安徽省区域内断层[10]。
|
图 3 AHCORS在ITRF2008框架下水平速度场 Fig. 3 Horizontal velocity field of AHCORS under ITRF2008 frame |
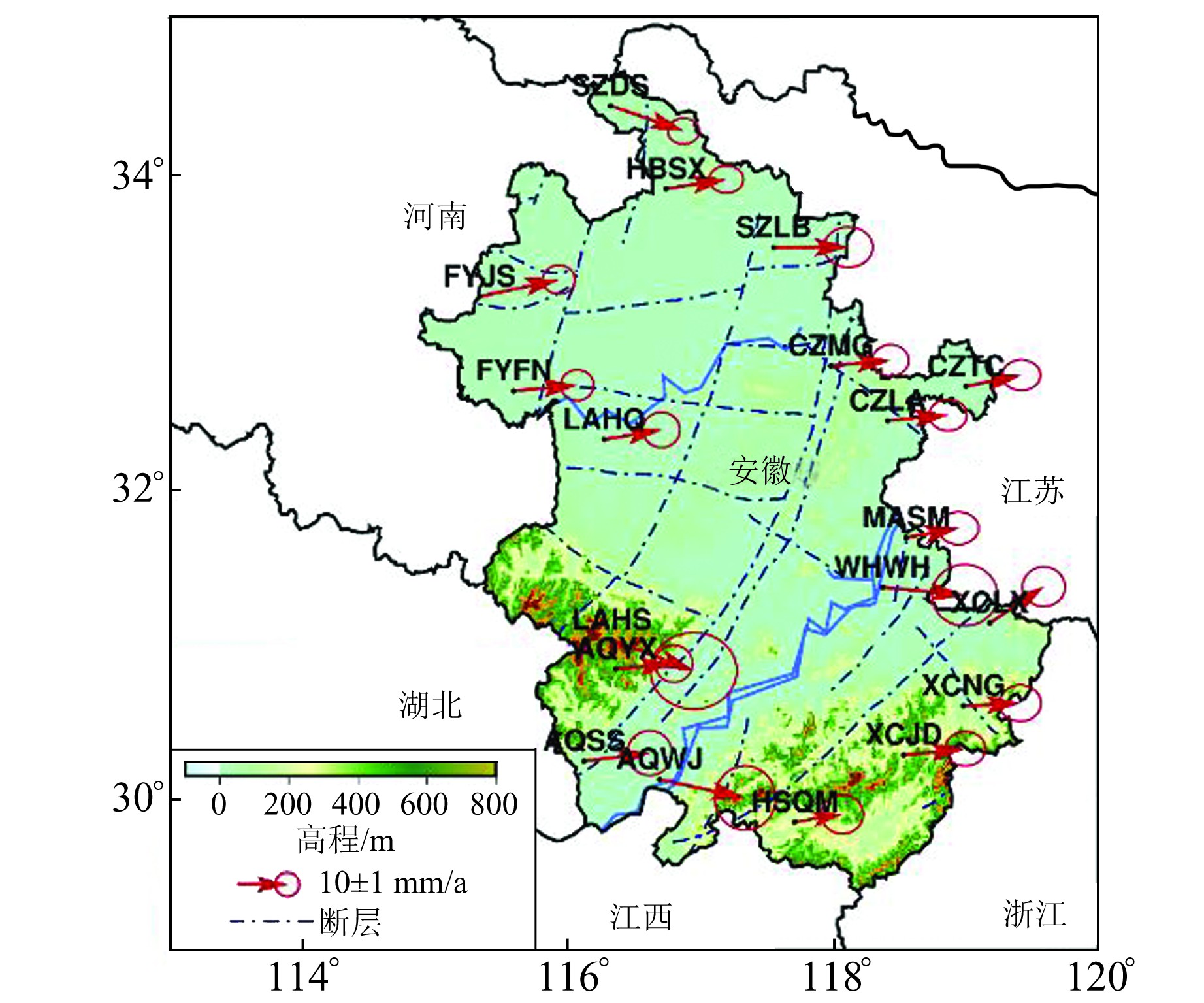
根据式(4)求得AHCORS以欧亚板块为运动背景场框架下的水平速度场为:N方向最大值为3.50 mm/a, 最小值为-3.00 mm/a, 平均值为0.29 mm/a; E方向最大值为8.31 mm/a, 最小值为4.60 mm/a, 平均值为6.27 mm/a。相对于欧亚板块运动的水平速度场如图 4所示。由图可知,以欧亚板块作为参考框架,安徽省CORS各站的运动方向较为一致,均为东南方向,其平均速率为6.28mm/a, 方向为E2.65°N。另外,计算中国大陆及其周边5个IGS站点相对于亚欧板块的速度场,得到的速度趋势与Zhao等[11]的一致。
|
图 4 AHCORS在欧亚框架下水平速度场 Fig. 4 Horizontal velocity field of AHCORS under Eurasian frame |
图 5表示参考站的垂直速度场。由图可见,安徽省陆地垂直运动的总体规律为:以淮河为界,以南呈隆起趋势,以北有大面积沉降,垂直方向整体平均运动速率为-0.71 mm/a。其中,大别山地区的隆起速率大于江淮丘陵区和黄山地区,最大隆起速度为6.96 mm/a, 该峰值发生在安庆望江(AQWJ)站;江淮丘陵区抬升相对平缓,平均抬升速率为2.0 mm/a; 黄山地区的平均隆升速率约为3.6 mm/a。淮北地区沉降明显,最大沉降速率为32.82 mm/a, 发生在宿州砀山(SZDS)站。
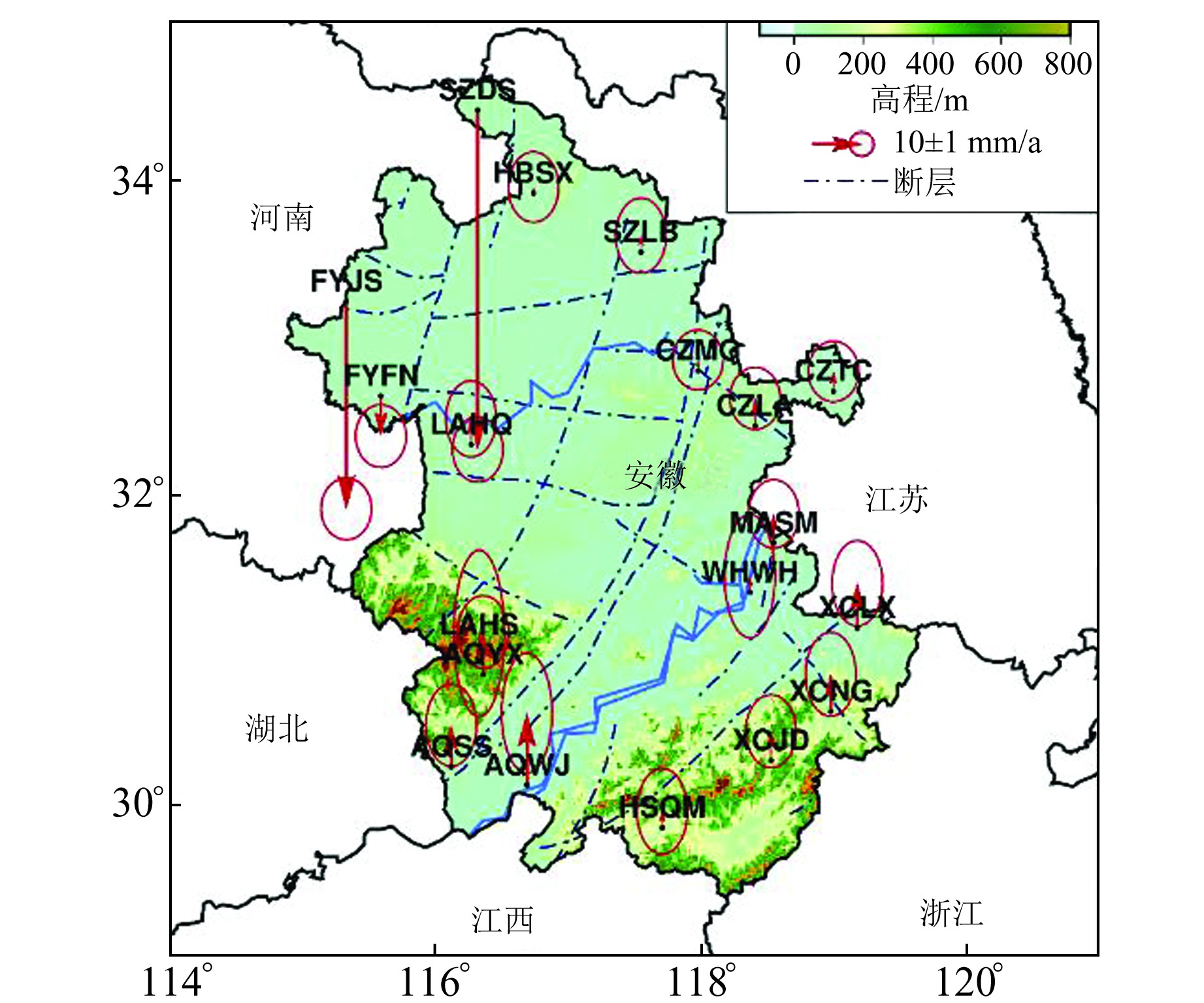
|
图 5 AHCORS垂直速度场 Fig. 5 Vertical velocity field of AHCORS |
本文结果与袁鹏等[5]对2011~2013年AHCORS坐标时间序列的速度场分析结果相似。主要区别在于,本文淮北地区台站沉降的最大值为32.82 mm/a, 远大于2011~2013年计算值13.50 mm/a。其原因可能有:1)本文解算的时间跨度比之前文献长,而时间跨度对噪声模型和速度估计均有较大影响,在小于10 a的时间跨度内,随着时间尺度的增加,参考站的速度以及不确定度会逐渐由发散趋于收敛[12-13]; 2)随着矿产资源的开采,该区域的地表沉降速度有逐渐加速的趋势。
4 结语1) 为了得到适用于AHCORS坐标时间序列的最优噪声组合模型,对周期图法获取的各方向噪声序列的功率谱密度进行分析。结果表明,安徽省境内参考站的最佳噪声模型为白噪声+闪烁噪声(WN+FN)模型。若未考虑时间序列中的有色噪声,则会明显低估速度项的误差。
2) 采用WN+FN噪声模型对AHCORS坐标序列建模,获取ITRF2008框架下三维方向速度场。结果表明,参考站水平方向平均运动速度为31.72 mm/a, 方向为E22.76°S。为了进一步获取AHCORS水平差异性运动,将水平运动速度从ITRF2008框架转化到相对于欧亚板块的运动速度。结果表明,以欧亚板块为参考的平均运动速度为6.28 mm/a, 方向为E2.65°N。垂直方向上,以淮河为界呈现出南方隆升、北方沉降的趋势。淮河以北有大面积沉降,大别山地区的隆起速率大于江淮丘陵区和黄山地区,最大隆起速度为6.96 mm/a; 江淮丘陵区抬升速率相对平缓,平均抬升速率为2.0 mm/a; 黄山地区的平均隆升速率约为3.6 mm/a。淮北地区沉降明显,最大沉降速率为32.82 mm/a, 发生在SZDS站,该地区的明显沉降可能是近年来开采矿产资源所致。
| [1] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报: 信息科学版, 2018, 43(12): 2 112-2 123 (Jiang Weiping, Wang Kaihua, Li Zhao, et al. Prospect and Theory of GNSS Coordinate Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 112-2 123)
(  0) 0) |
| [2] |
姜卫平. 卫星导航定位基准站网的发展现状、机遇与挑战[J]. 测绘学报, 2017, 46(10): 1 379-1 388 (Jiang Weiping. Challenges and Opportunities of GNSS Reference Station Network[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 379-1 388)
(  0) 0) |
| [3] |
郑先进, 刘东旺, 刘泽民, 等. 安徽地区应力场分区特征及中强震前震源机制的一致性研究[J]. 华北地震科学, 2010(1): 16-20 (Zheng Xianjin, Liu Dongwang, Liu Zemin, et al. The Characteristics of Regional Stress Field in Anhui Area and the Coherence Characteristics of Focal Mechanism Solutions before Mid-Strong Earthquakes[J]. North China Earthquake Sciences, 2010(1): 16-20)
(  0) 0) |
| [4] |
骆佳骥, 周冬瑞, 于书媛, 等. 郯庐断裂带(安徽段)活动特征及现代应力状态研究综述[J]. 防灾科技学院学报, 2016, 18(2): 10-18 (Luo Jiaji, Zhou Dongrui, Yu Shuyuan, et al. Review of Activity Characteristics and Regional Stress State of Tan-Lu Fault Zone(Anhui Segment)[J]. Journal of Institute of Disaster Prevention, 2016, 18(2): 10-18)
(  0) 0) |
| [5] |
袁鹏, 孙宏飞, 秦昌威, 等. 安徽CORS参考站三维速度场分析[J]. 武汉大学学报: 信息科学版, 2016, 41(4): 535-540 (Yuan Peng, Sun Hongfei, Qin Changwei, et al. Analysis of Anhui CORS Reference Stations 3D Velocity Field[J]. Geomatics and Information Science of Wuhan University, 2016, 41(4): 535-540)
(  0) 0) |
| [6] |
黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-33 (Huang Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 31-33)
(  0) 0) |
| [7] |
Williams S D P, Bock Y, Fang P. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B3)
(  0) 0) |
| [8] |
Williams S D P. CATS: GPS Coordinate Time Series Analysis Software[J]. GPS Solutions, 2008, 12(2): 147-153 DOI:10.1007/s10291-007-0086-4
(  0) 0) |
| [9] |
李延兴, 胡新康, 帅平, 等. 中国大陆地壳水平运动速度场与应变场[J]. 国际地震动态, 2002, 32(7): 1-9 (Li Yanxing, Hu Xinkang, Shuai Ping, et al. The Velocity Fields and Strain Fields of Horizontal Crust Motion of the Mainland of China[J]. Recent Developments in World Seismology, 2002, 32(7): 1-9 DOI:10.3969/j.issn.0253-4975.2002.07.001)
(  0) 0) |
| [10] |
邓起东, 张培震, 冉勇康, 等. 中国活动构造与地震活动[J]. 地学前缘, 2003, 10(S1): 66-73 (Deng Qidong, Zhang Peizhen, Ran Yongkang, et al. Active Tectonics and Earthquake Activities in China[J]. Earth Science Frontiers, 2003, 10(S1): 66-73)
(  0) 0) |
| [11] |
Zhao B, Huang Y, Zhang C H, et al. Crustal Deformation on the Chinese Mainland during 1998—2014 Based on GPS Data[J]. Geodesy and Geodynamics, 2015, 6(1): 7-15
(  0) 0) |
| [12] |
姜卫平, 周晓慧. 澳大利亚GPS坐标时间序列跨度对噪声模型建立的影响分析[J]. 中国科学: 地球科学, 2014, 44(11): 2 461-2 478 (Jiang Weiping, Zhou Xiaohui. Effect of the Span of Australian GPS Coordinate Time Series in Establishing an Optimal Noise Model[J]. Science China: Earth Sciences, 2014, 44(11): 2 461-2 478)
(  0) 0) |
| [13] |
贺小星, 花向红, 鲁铁定, 等. 时间跨度对GPS坐标序列噪声模型及速度估计影响分析[J]. 国防科技大学学报, 2017, 39(6): 12-18 (He Xiaoxing, Hua Xianghong, Lu Tieding, et al. Effect of Time Span on GPS Time Series Noise Model and Velocity Estimation[J]. Journal of National University of Defense Technology, 2017, 39(6): 12-18)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


