2. 北京跟踪与通信技术研究所, 北京市北清路26号, 100094;
3. 西安测绘研究所, 西安市雁塔路中段1号, 710054;
4. 信息工程大学地理空间信息学院, 郑州市科学大道62号, 450001
对于日渐完善的北斗系统,其定位精度和空间几何分布受到国内外学者的极大关注。但是,现阶段还未有学者针对BDS-3的B1I-B3I、B1C-B2a两种双频组合的PPP精度进行比较。本文利用MGEX观测站数据,对BDS-3精密单点定位的非差非组合模型与无电离层组合模型定位性能进行对比分析。
1 基于卫星端DCB的精密钟差改正模型卫星信号从卫星内部产生到离开卫星发射天线的时间称为卫星内部时延,2个不同频率的信号或同一频率不同测距码之间的时延差是不同的。直接测定信号内部时延较为困难,所以一般采用2个信号的时延之差来处理。BDS卫星端差分码偏差可达20 ns, 对于cm级别的精密单点定位影响很大;接收机端差分码偏差可被吸收到接收机钟差内一起计算。
1.1 BDS卫星端DCB改正模型目前共有3家分析中心发布BDS-3精密轨道和钟差产品,分别是德国地学研究中心产品(GBM)、武汉大学产品(WUM)和西安测绘研究所产品(XRI), 三者都是基于B1、B3频点无电离层组合解算得到的,因此使用不同频点组合进行精密单点定位,其对应的DCB改正模型不同。B1I和B3I组成无电离层组合的方程为:
| $P_{\mathrm{IF}}=\rho_{\mathrm{r}}+c \cdot \overline{\mathrm{d}} t_{\mathrm{r}}-c \cdot \mathrm{d} t_{\mathrm{s}}+c \cdot\left(f_{1\mathrm{I}}^{2} \cdot \tau_{1\mathrm{I}}^{\mathrm{s}}-\right. \\ \left.f_{3\mathrm{I}}^{2} \cdot \tau_{3\mathrm{I}}^{\mathrm{s}}\right) /\left(f_{1\mathrm{I}}^{2}-f_{3\mathrm{I}}^{2}\right)+d_{\mathrm{trop}}+m_{i}^{\mathrm{IF}}+\varepsilon_{\mathrm{IF}}$ | (1) |
式中,r、s分别代表接收机和卫星,c为光速,miIF为伪距的多路径误差,εIF为观测噪声,dtr为吸收接收机硬件延迟的接收机钟差,τ1I、τ3I分别为B1I、B3I频点的卫星端硬件延迟参数。则精密产品中的卫星钟差可表示为:
| $\overline{\mathrm{d}} t_{s}=\mathrm{d} t_{s}-\left(f_{1 \mathrm{I}}^{2} \cdot \tau_{1 \mathrm{I}}^{s}-f_{3 \mathrm{I}}^{2} \cdot \tau_{3 \mathrm{I}}^{s}\right) /\left(f_{1 \mathrm{I}}^{2}-f_{3 \mathrm{I}}^{2}\right)$ | (2) |
由此看出,当利用B1I、B3I频点无电离层组合定位时,不需要进行DCB改正。当采用B1C和B2a组合时,其卫星钟差参数可表示为:
| $\overline{\mathrm{d}} t_{\mathrm{s}(\mathrm{BIC}, \mathrm{B} 2 \mathrm{a})}=\mathrm{d} t_{\mathrm{s}}-\left(f_{1 \mathrm{C}}^{2} \cdot \tau_{\mathrm{1C}}^{\mathrm{s}}-f_{2 \mathrm{a}}^{2} \cdot \tau_{2 \mathrm{a}}^{\mathrm{s}}\right) / \\ \left(f_{1 \mathrm{C}}^{2}-f_{2 \mathrm{a}}^{2}\right)$ | (3) |
将其归算到B1I和B3I组合基准下,即将式(2)代入式(3), 可得:
| $\overline{\mathrm{d}} t_{\mathrm{s}(\mathrm{BlC}, \mathrm{B} 2 \mathrm{a})}=\overline{\mathrm{d}} t_{\mathrm{s}}-\left(f_{1 \mathrm{C}}^{2} \cdot \tau_{1 \mathrm{C}}^{\mathrm{s}}-f_{2 \mathrm{a}}^{2} \cdot \tau_{2 \mathrm{a}}^{\mathrm{s}}\right) / \\ \left(f_{1 \mathrm{C}}^{2}-f_{2 \mathrm{a}}^{2}\right)+\left(f_{1 \mathrm{I}}^{2} \cdot \tau_{1 \mathrm{I}}^{\mathrm{s}}-f_{3 \mathrm{I}}^{2} \cdot \tau_{3 \mathrm{I}}^{\mathrm{s}}\right) /\left(f_{1 \mathrm{I}}^{2}-f_{3 \mathrm{I}}^{2}\right)$ | (4) |
在DCB产品中,各参数定义为:
| $\left\{\begin{array}{l}\mathrm{DCB}_{1 \mathrm{X}-5 \mathrm{X}}=\tau_{1 \mathrm{C}}^{\mathrm{s}}-\tau_{2 \mathrm{a}}^{\mathrm{s}} \\ \mathrm{DCB}_{1 \mathrm{X}-6 \mathrm{I}}=\tau_{1 \mathrm{C}}^{\mathrm{s}}-\tau_{3 \mathrm{I}}^{\mathrm{s}} \\ \mathrm{DCB}_{2 \mathrm{I}-6 \mathrm{I}}=\tau_{1 \mathrm{I}}^{\mathrm{s}}-\tau_{3 \mathrm{I}}^{\mathrm{s}}\end{array}\right.$ | (5) |
进行等式代换后可得:
| $\overline{\mathrm{d}} t_{\mathrm{s}(\mathrm{BlC}, \mathrm{B} 2 \mathrm{a})}=\overline{\mathrm{d}} t_{\mathrm{s}}+\left(f_{1 \mathrm{I}}^{2} \cdot \mathrm{DCB}_{2 \mathrm{I}-6 \mathrm{I}}\right) /\left(f_{1 \mathrm{I}}^{2}-f_{3 \mathrm{I}}^{2}\right)- \\ \mathrm{DCB}_{1 \mathrm{X}-6 \mathrm{I}}-\left(f_{2 \mathrm{a}}^{2} \cdot \mathrm{DCB}_{1 \mathrm{X}-5 \mathrm{X}}\right) /\left(f_{1 \mathrm{C}}^{2}-f_{2 \mathrm{a}}^{2}\right)$ | (6) |
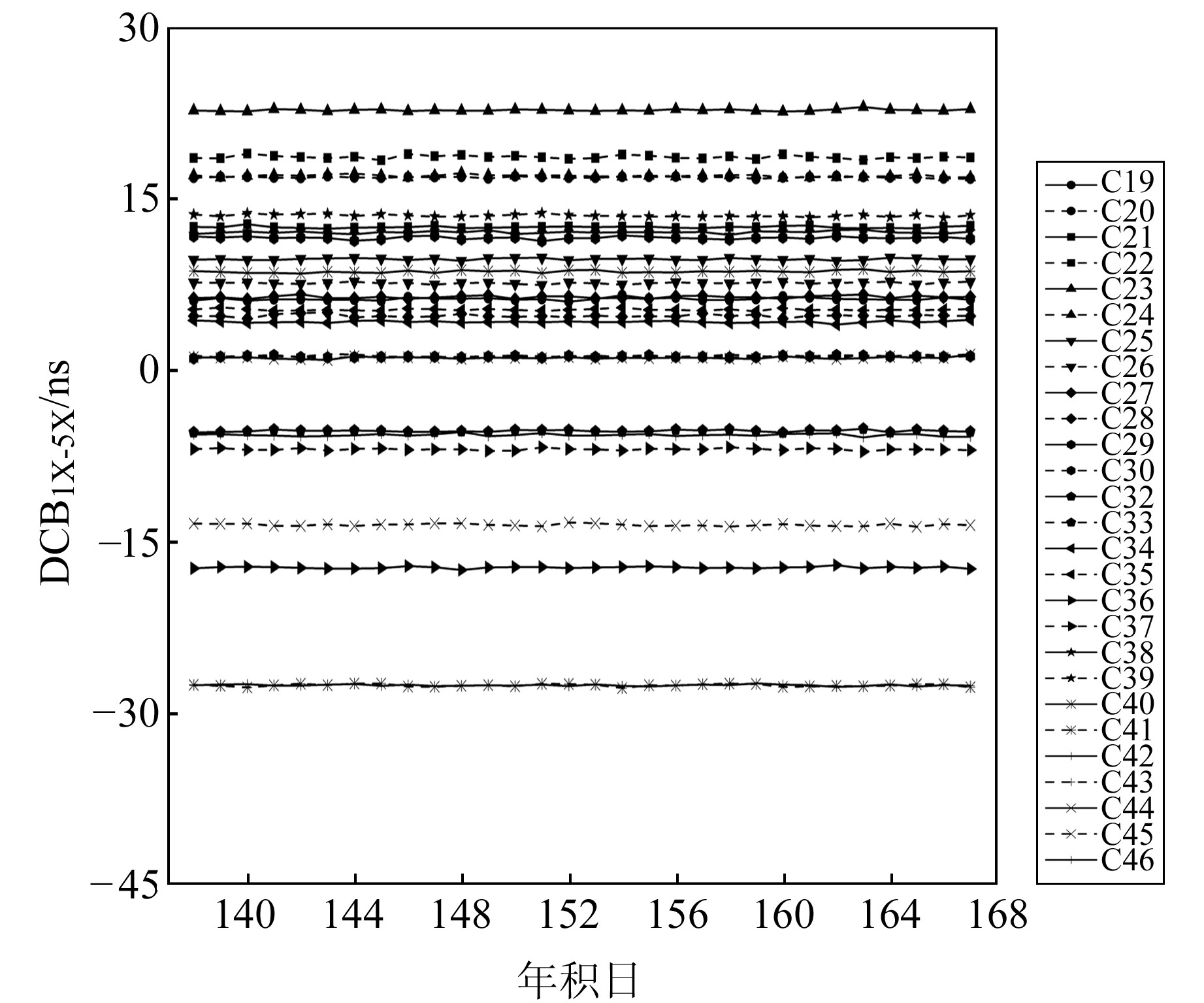
由上文可知,北斗三号DCB产品的质量将直接影响B1C-B2a双频组合PPP的定位精度,因此对上述DCB产品中的3个参数的稳定性进行分析。现阶段共有2种支持BDS的DCB产品[1], 一种是由德国宇航中心(DLR)利用全球MGEX站计算的高精度电离层模型(GIM)修正卫星信号在传播路径上的电离层延迟,从而计算出卫星和接收机的差分码偏差[2-4]; 另一种是中国科学院利用观测站数据建立电离层TEC模型并解算卫星以及接收机的差分码偏差[5-6]。自2019-11开始,中国科学院发布的DCB产品支持MGEX和iGMAS的B1C、B2a频点的观测数据。实验数据选取2020-05-17~06-15(doy 138~167)中国科学院发布的码偏差产品,图 1、2、3分别为DCBC1X-C5X、DCBC1X-C6I、DCBC2I-C6I的日解值,其中DCBC1X-C5X代表B1C和B2a之间的频间偏差,DCBC1X-C6I代表B1C和B3I之间的频间偏差,DCBC2I-C6I代表B1I和B3I之间的频间偏差。表 1给出了BDS-3卫星3个码偏差产品的标准差和均值。
|
图 1 BDS-3卫星DCBC1X-C5X值 Fig. 1 The values of BDS-3 DCBC1X-C5X |
|
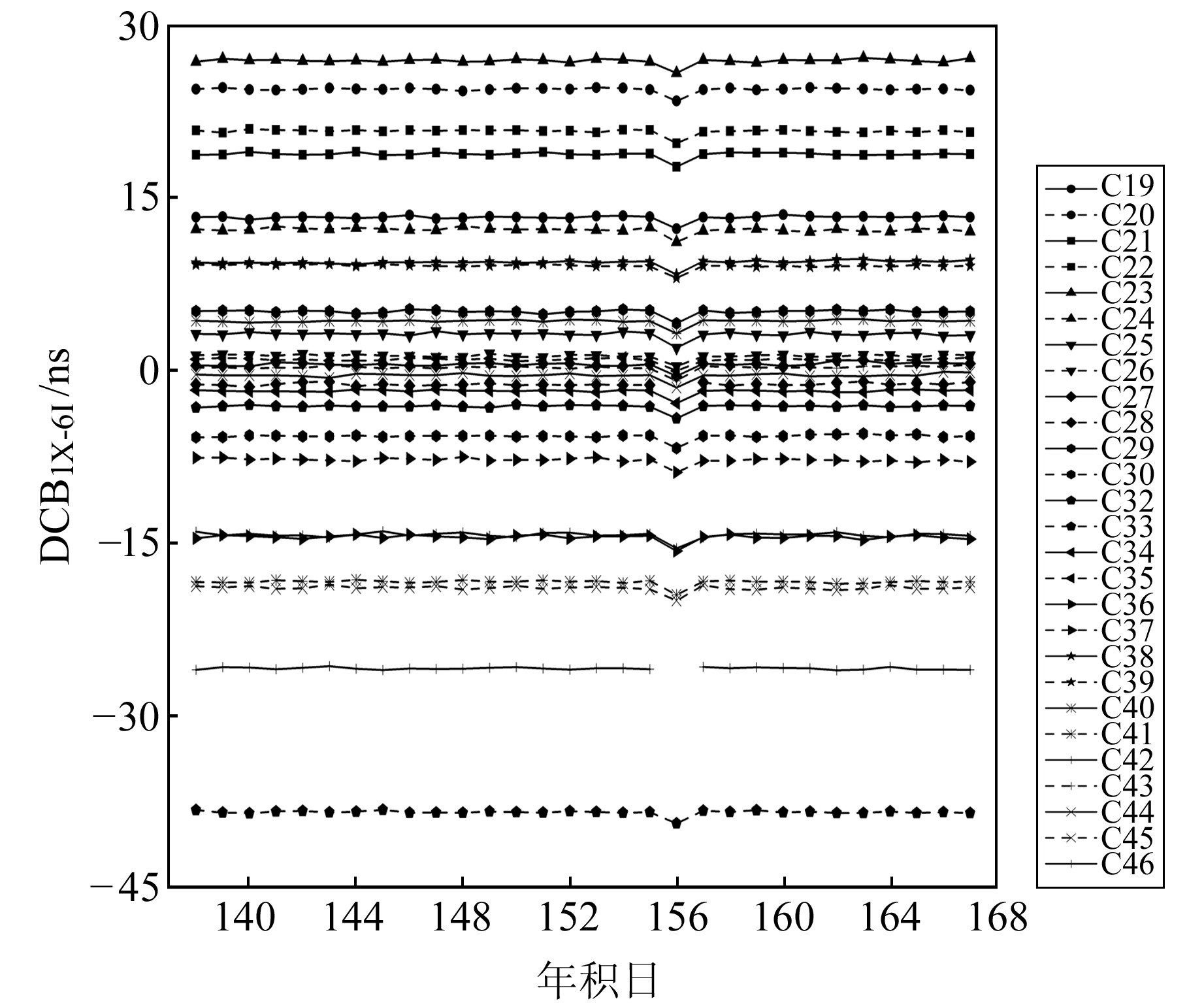
图 2 BDS-3卫星DCBC1X-C6I值 Fig. 2 The values of BDS-3 DCBC1X-C6I |
|
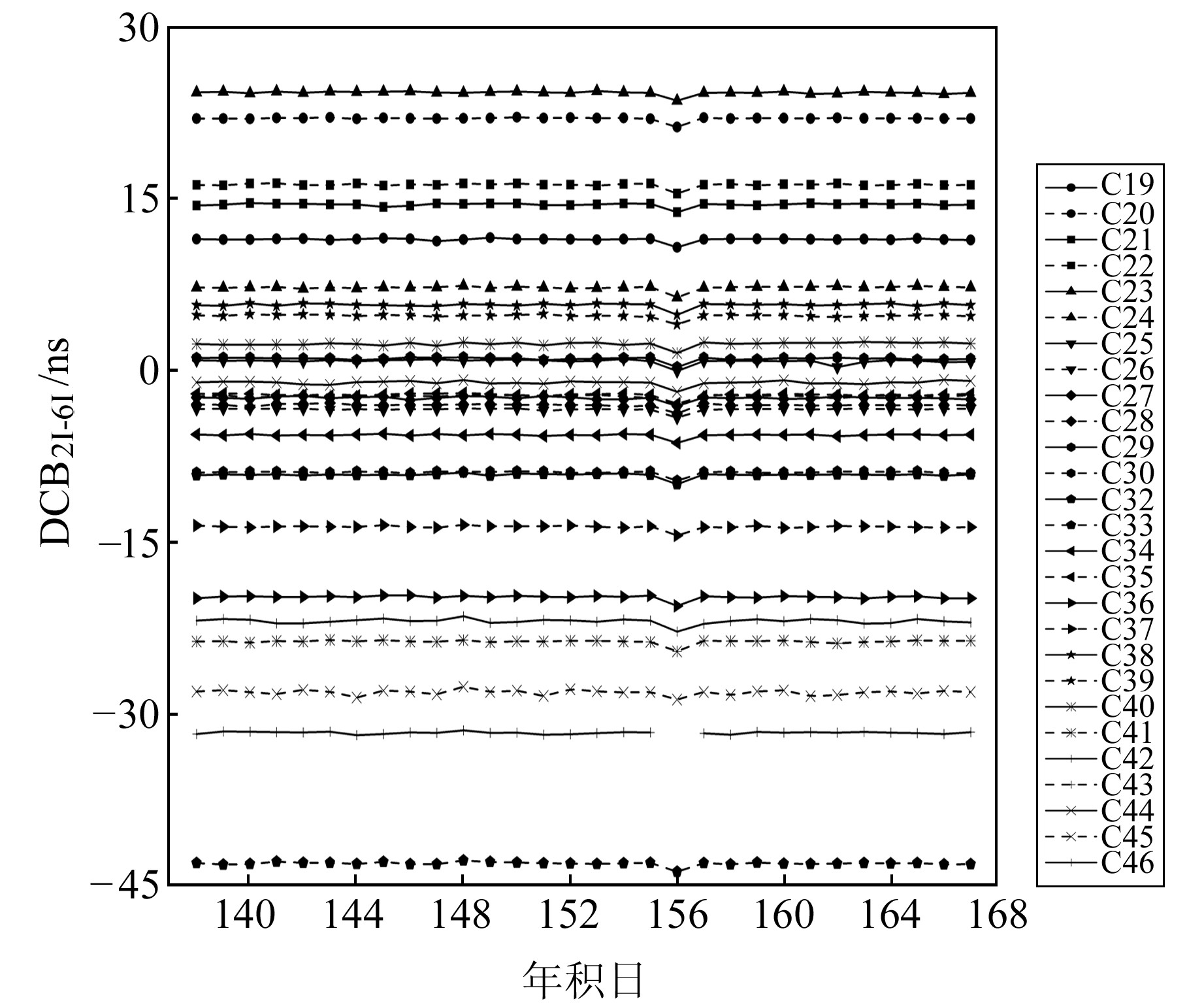
图 3 BDS-3卫星DCBC2I-C6I值 Fig. 3 The values of BDS-3 DCBC2I-C6I |
|
|
表 1 BDS-3卫星DCB产品的标准差 Tab. 1 The standard deviation of BDS-3 DCB |
由图 2、3可以看出,C42卫星在doy 156的DCBC1X-C6I、DCBC2I-C6I值缺失,导致当天其他BDS-3卫星的DCB值发生明显波动,这可能是因为用于解算DCB的观测值中缺少C42卫星B3I频点的观测数据[7]。除此之外,3种DCB值在1个月内变化较为平稳,基本都在0.5 ns范围内波动。由表 1可以看出,DCBC1X-C5X的范围在-28~23 ns之间,其标准差都在0.100 ns左右;DCBC1X-C6I、DCBC2I-C6I的范围在-45~30 ns之间,平均标准差分别为0.210 ns、0.158 ns。由此可见,DCBC1X-C5X的稳定度优于DCBC2I-C6I、DCBC1X-C6I。
2 算例分析为了评估BDS-3精密单点定位不同模型的定位性能,分别进行静态和模拟动态实验,从定位精度和收敛时间2个方面对比非差非组合和无电离层组合模型下的B1I-B3I、B1C-B2a双频组合的PPP定位性能。选取2020-05-30~06-05(doy 151~157)MGEX观测网中GCGO、UNB3、RGDG、NYA2、BRST、SUTM、SGOC、KRGG、ULAB、WUH2等10个测站的实测数据进行实验。由于北斗三号的GEO卫星不播发B1C和B2a信号,因此将其剔除,只选取C19~C46卫星参与计算。实验真实坐标来源于IGS提供的站坐标天解文件,表 2给出PPP处理策略。
|
|
表 2 精密单点定位处理策略 Tab. 2 The processing strategy of PPP |
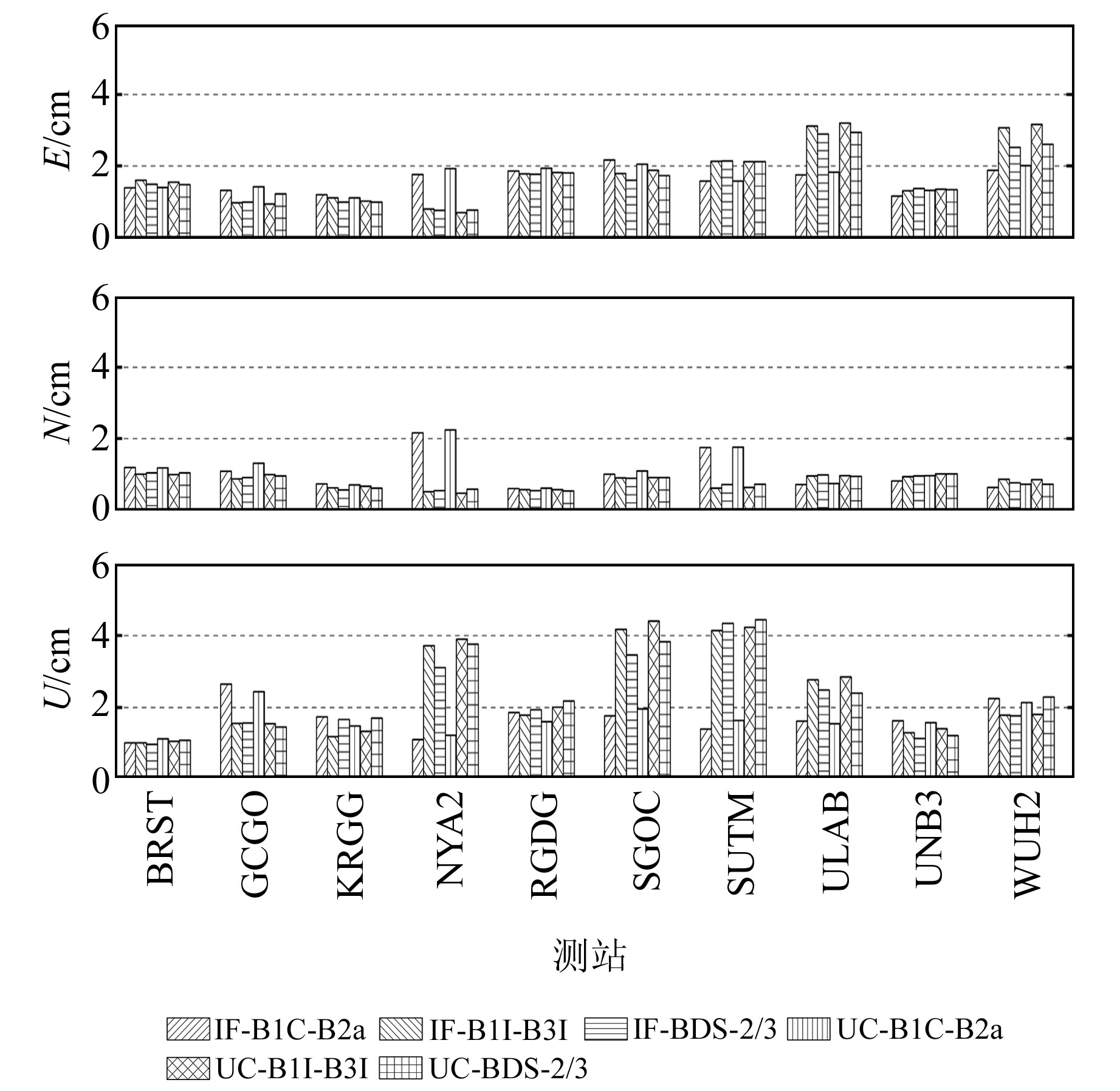
图 4给出了10个测站6种模型连续7 d的单天静态解在E、N、U方向的RMS的平均值,其中IF-BDS-2/3和UC-BDS-2/3分别表示BDS-2+BDS-3的B1I-B3I双频组合的无电离层组合和非差非组合模型。表 3统计了所有测站连续7 d的单天静态解在E、N、U和三维方向的RMS的平均值。由图 4和表 3可以看出,各个模型的静态RMS在E方向上都优于1.8 cm, N方向优于1.1 cm, U方向优于2.5 cm, 三维方向优于3.3 cm。对表 3中BDS-3的不同双频组合的无电离层和非差非组合模型的E、N、U方向定位精度取平均值,可以得出无电离层组合模型平均定位精度分别为1.7 cm、0.9 cm、2.1 cm, 非差非组合模型的分别为1.73 cm、0.9 cm、2.2 cm, 二者静态定位精度基本一致。对于不同定位模型的2种双频组合,B1C-B2a双频组合的平均定位精度分别为1.65 cm、1.1 cm、1.7 cm, B1I-B3I双频组合的则分别为1.8 cm、0.8 cm、2.4 cm, 可见B1C-B2a、B1I-B3I双频组合静态定位精度基本相当。BDS-2是区域卫星导航系统,服务范围在55°S~55°N、70°E~150°E, 本文实验中WUH2和SGOC测站在其范围内。比较2个测站BDS-3和BDS-2/3定位的精度可以得出,BDS-2/3较BDS-3在三维方向上精度平均提升9.4%。
|
图 4 6种PPP模型10个测站单天静态定位平均RMS Fig. 4 Average of RMS for 10 stations of 6 PPP models in daily static solutions |
|
|
表 3 6种PPP模型单天静态和模拟动态定位平均RMS Tab. 3 Average of RMS of 6 PPP models in daily static and kinematic solutions |
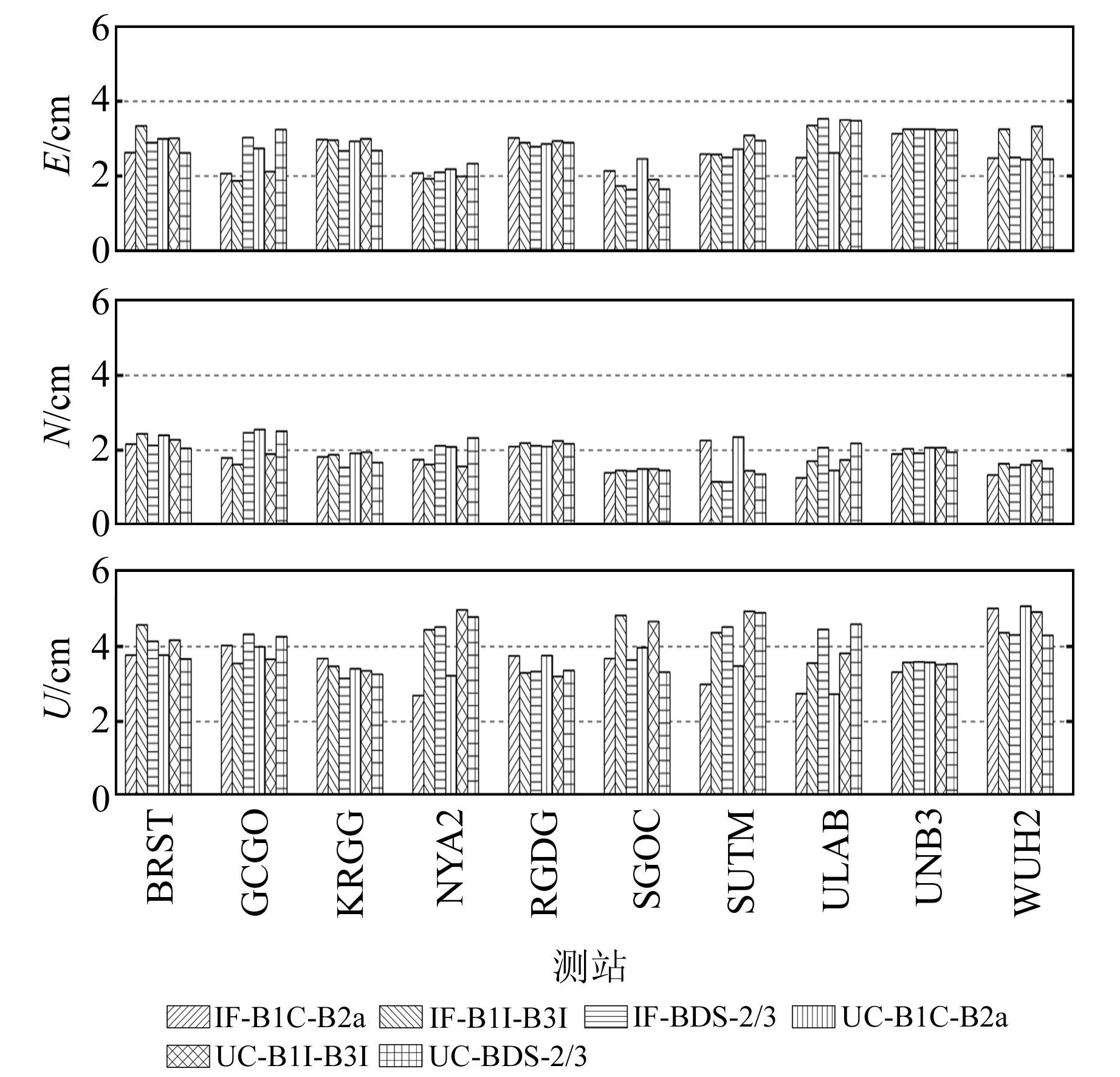
采用与静态实验相同的处理策略进行模拟动态实验。图 5给出了10个测站6种模型连续7 d的单天动态解在E、N、U方向的RMS的平均值。由图 5和表 3可以看出,10个测站6种模型的RMS在E、N、U方向上分别优于2.8 cm、2.0 cm、4.1 cm, 三维方向优于5.4 cm。模拟动态的无电离层组合在3个方向的平均定位精度分别为2.63 cm、1.8 cm、3.87 cm, 非差非组合的分别为2.73 cm、1.9 cm、3.93 cm, 二者动态定位精度相当。双频组合方面,B1C-B2a双频组合在3个方向的平均定位精度分别为2.65 cm、1.9 cm、3.65 cm, B1I-B3I双频组合的分别为2.75 cm、1.8 cm、4.05 cm, 可见2种双频组合动态定位精度基本一致。对WUH2和SGOC测站而言,BDS-2/3较BDS-3在三维方向上精度平均提升13.1%。
|
图 5 6种PPP模型10个测站单天模拟动态定位平均RMS Fig. 5 Average of RMS for 10 stations of 6 PPP models in daily kinematic solutions |
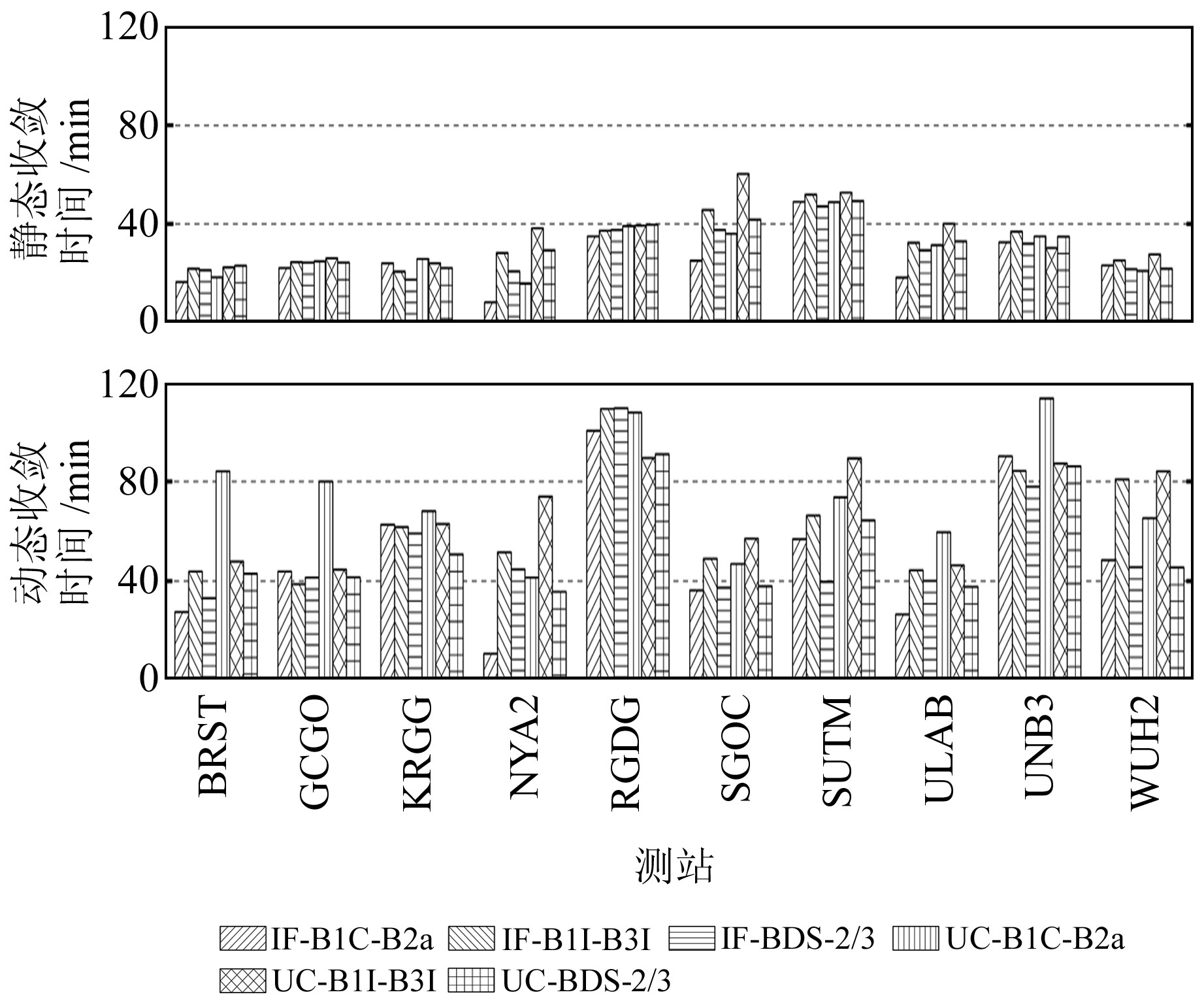
为了分析不同双频组合和不同定位模型的收敛时间,对上述10个测站连续7 d的观测数据进行静态和模拟动态PPP计算,并统计各测站E、N、U分量定位误差连续20个历元均小于1 dm所需要的时间。图 6给出了各个测站连续7 d静态和模拟动态定位收敛时间的平均值,表 4统计了所有测站连续7 d静态和模拟动态定位收敛时间的平均值。
|
图 6 6种PPP模型10个测站单天静态和模拟动态平均收敛时间 Fig. 6 Average convergence time of 6 PPP models for 10 stations in daily static and kinematic solutions |
|
|
表 4 6种PPP模型静态和模拟动态定位平均收敛时间 Tab. 4 Average convergence time of 6 PPP models in daily static and kinematic solutions |
由图 6可以看出,10个测站静态定位收敛时间基本都在50 min以内,动态定位收敛时间基本在90 min以内。对表 4中各种模型定位收敛时间取平均值,可以得到BDS-3静态定位平均收敛时间在31 min左右,动态定位则在60 min左右。静态定位中在无电离层组合和非差非组合模型下的B1C-B2a双频组合较B1I-B3I收敛时间平均减少7 min左右,动态定位平均减少13 min左右。在B1C-B2a、B1I-B3I双频组合下,无电离层组合模型静态和动态的平均收敛时间分别为约29 min、57 min, 非差非组合模型的则分别为约33 min、62 min, 由此可以看出,无电离层组合与非差非组合模型收敛时间基本一致。WUH2和SGOC站的BDS-2/3静态收敛时间较BDS-3平均提升22.8%, 动态收敛时间平均提高38.7%。
3 结语本文推导出BDS-3新频点B1C-B2a组合卫星端DCB改正模型,同时利用全球分布的10个MGEX站7 d的观测数据以及西安测绘研究所发布的精密轨道钟差产品,进行不同定位模型和不同双频组合的静态和模拟动态PPP实验,并分析各个模型的定位精度和收敛时间。结果显示,BDS-3静态精密单点定位在水平方向的RMS优于2.0 cm, 高程方向优于2.5 cm, 平均收敛时间在31 min左右。模拟动态定位的水平方向RMS优于3.4 cm, 高程方向优于4.1 cm, 平均收敛时间在60 min左右。对于亚太地区的2个测站,静态定位中,BDS-2/3较BDS-3在三维方向上精度平均提升9.4%, 收敛时间平均提升22.8%;动态定位中,三维方向上精度平均提升13.1%, 收敛时间平均提升38.7%。
由于全球范围内可以同时观测BDS-3四个频点的观测站较少,本文仅采用10个全球分布的MGEX站进行研究。通过本文实验结果看到,B1I-B3I和B1C-B2a双频组合的定位精度相当,收敛时间较为接近,且二者均适用于北斗精密单点定位。随着精密轨道和钟差产品精度的提高以及其他精密产品的完善,BDS-3全球精密单点定位性能将会进一步提升。
| [1] |
梅登奎, 闻德保. MGEX北斗差分码偏差两种精确处理方法对比分析[J]. 空间科学学报, 2019, 39(5): 662-669 (Mei Dengkui, Wen Debao. Comparative Analysis of Two Precise Processing Methods for MGEX BDS Differential Code Biases[J]. Chinese Journal of Space Science, 2019, 39(5): 662-669)
(  0) 0) |
| [2] |
Montenbruck O, Hauschild A, Steigenberger P. Differential Code Bias Estimation Using Multi-GNSS Observations and Global Ionosphere Maps[J]. Navigation, 2014, 61(3): 191-201 DOI:10.1002/navi.64
(  0) 0) |
| [3] |
Li X X, Xie W L, Huang J X, et al. Estimation and Analysis of Differential Code Biases for BDS3/BDS2 Using iGMAS and MGEX Observations[J]. Journal of Geodesy, 2019, 93(3): 419-435 DOI:10.1007/s00190-018-1170-y
(  0) 0) |
| [4] |
张强, 赵齐乐, 章红平, 等. 利用北斗观测实验网解算北斗卫星差分码偏差[J]. 武汉大学学报: 信息科学版, 2016, 41(12): 1 649-1 655 (Zhang Qiang, Zhao Qile, Zhang Hongping, et al. BDS Differential Code Bias Estimation Using Beidou Experimental Tracking Stations[J]. Geomatics and Information Science of Wuhan University, 2016, 41(12): 1 649-1 655)
(  0) 0) |
| [5] |
Li Z S, Yuan Y B, Li H, et al. Two-Step Method for the Determination of the Differential Code Biases of COMPASS Satellites[J]. Journal of Geodesy, 2012, 86(11): 1 059-1 076 DOI:10.1007/s00190-012-0565-4
(  0) 0) |
| [6] |
Wang N B, Yuan Y B, Li Z S, et al. Determination of Differential Code Biases with Multi-GNSS Observations[J]. Journal of Geodesy, 2016, 90(3): 209-228 DOI:10.1007/s00190-015-0867-4
(  0) 0) |
| [7] |
Wang Q S, Jin S G, Yuan L L, et al. Estimation and Analysis of BDS-3 Differential Code Biases from MGEX Observations[J]. Remote Sensing, 2019, 12(1): 68 DOI:10.3390/rs12010068
(  0) 0) |
2. Beijing Institute of Tracking and Telecommunications Technology, 26 Beiqing Road, Beijing 100094, China;
3. Xi'an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China;
4. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2021, Vol. 41
2021, Vol. 41


