2. 北京理工大学化工与环境学院, 北京市中关村南大街5 号, 100081
相对于其他非线性滤波方法,UKF算法因其计算量小、精度高的特点,被广泛应用于导弹制导、空间探索等各个领域。但随着系统维数和非线性度的增加,其效果会变差[1]。且UKF算法存在对滤波器初始值选取比较敏感的问题,同时系统状态模型的异常扰动也会对滤波精度带来一定影响[2]。
为此,本文将自适应原理与UKF算法相结合,得到一种改进的UKF算法。该算法能够自行判断系统是否异常,并利用自适应因子自发调节导航解的结构。将改进后的UKF算法应用于BDS/SINS组合导航,验证其克服常规UKF滤波算法缺陷的能力。
1 UKF算法 1.1 UKF算法概述UKF本质上也是线性的最小方差估计,是建立在模型基础上的算法。标准卡尔曼滤波需保证系统的状态方程与量测方程均为线性,而UKF算法在计算最佳增益阵的过程中,对量测方程以及状态方程的性质没有任何具体的约束,所以其既可以在线性条件下使用,也可以在非线性条件下使用[2]。
设系统状态方程和量测方程为:
| $\left\{\begin{array}{l}\boldsymbol{X}_{k}=f\left(\boldsymbol{X}_{k-1}, \boldsymbol{u}_{k-1}, \boldsymbol{W}_{k-1}\right) \\ \boldsymbol{Z}_{k}=h\left(\boldsymbol{X}_{k}, \boldsymbol{V}_{k}\right)\end{array}\right.$ | (1) |
式中,k-1、k为离散时刻;Xk-1为上一时刻的状态估计,其方差阵为Pk-1; uk-1为系统确定性控制项;Wk-1为系统噪声,其方差阵为Qk-1; Zk为量测值;Vk为量测噪声,其方差阵为Rk。系统和量测噪声均服从高斯分布。UKF算法的任务是在已知状态初始值X0、系统确定性控制序列u0, u1, …, uk-1以及量测值序列Z1, Z2, …, Zk的情况下,估计系统的状态变量Xk。
UKF算法采用递推计算方式,包括2个过程:状态预测和修正计算。已知状态变量的维数为n, UKF算法用UT变换的方式获取2n+1个采样点(sigma点)实现状态及其相关统计量的递推计算[3]。UKF算法具体计算步骤如下:
1) 初始化。状态向量初始化为X0, 初始化方差阵Pa, 初始化UKF算法比例因子α、β、κ。
2) 计算样本点。计算样本点集χ0i, i=0, 1, …, 2n, 计算sigma点的加权值Wim、Wic, i=0, 1, …, 2n。在k时刻(k=1, 2, …), 样本点及相应的权值按照式(2)求取:
| $\begin{aligned} \boldsymbol{X}_{k}^{0} &=\overline{\boldsymbol{X}}_{k-1} \\ \boldsymbol{x}_{k}^{i} &=\overline{\boldsymbol{X}}_{k-1}+\left(\sqrt{(n+\lambda) \boldsymbol{P}_{k-1}}\right)_{i}, i=1, \cdots, n \\ \boldsymbol{x}_{k}^{i} &=\overline{\boldsymbol{X}}_{k-1}-\left(\sqrt{(n+\lambda) \boldsymbol{P}_{k-1}}\right)_{i}, i=n+1, \cdots, 2 n \end{aligned} \\ \begin{aligned} W_{0}^{m} &=\frac{\lambda}{n+\lambda} \\ W_{0}^{c} &=\frac{\lambda}{n+\lambda}+\left(1-\alpha^{2}+\beta\right) \\ W_{i}^{m} &=W_{i}^{c}=\frac{1}{2(n+\lambda)}, i=1, \cdots, 2 n \end{aligned}$ | (2) |
3) 状态均值和方差的一步预测。以sigma点集χ0i作为UKF状态向量递推计算的初值,收集惯性传感器的输出原始数据,根据SINS的算法原理进行sigma点集的递推计算,得到k时刻的系统状态Xk/k-1i, i=0, 1, …, 2n。通过sigma点集得到的状态预测均值和方差为:
| $\hat{\boldsymbol{X}}_{k / k-1}=\sum\limits_{i=0}^{2 n} W_{i}^{m} \boldsymbol{X}_{k / k-1}^{i}$ | (3) |
| $\boldsymbol{P}_{k / k-1}=\sum\limits_{i=0}^{2 n} W_{i}^{c}\left(\boldsymbol{X}_{k / k-1}^{i}-\hat{\boldsymbol{X}}_{k / k-1}\right) \cdot \\ \left(\boldsymbol{X}_{k / k-1}^{i}-\hat{\boldsymbol{X}}_{k / k-1}\right)^{\mathrm{T}}$ | (4) |
4) 量测更新。在量测时刻,根据系统量测方程求取量测一步预测的传递值:
| $\boldsymbol{Z}_{k / k-1}^{i}=\boldsymbol{H} \boldsymbol{X}_{k / k-1}^{i}+\boldsymbol{V}_{i}, i=0, 1, \cdots, 2 n$ | (5) |
计算量测均值和方差:
| $\hat{\boldsymbol{Z}}_{k / k-1}=\sum\limits_{i=0}^{2 n} W_{i}^{m} \boldsymbol{Z}_{k / k-1}^{i}$ | (6) |
| $\boldsymbol{P}_{z z}=\sum\limits_{i=0}^{2 n} W_{i}^{c}\left(\boldsymbol{Z}_{k / k-1}^{i}-\hat{\boldsymbol{Z}}_{k / k-1}\right) \cdot \\ \left(\boldsymbol{Z}_{k / k-1}^{i}-\hat{\boldsymbol{Z}}_{k / k-1}\right)^{\mathrm{T}}$ | (7) |
5) 计算UKF增益,更新状态向量和方差。获得测量值及预测值后,进行新息计算,通过滤波增益矩阵,得到每个状态对应的误差修正量。UKF中新息及滤波增益的计算都涉及到状态预测点集、测量预测点集均值和方差的计算。
计算状态预测与量测估计的协方差:
| $\boldsymbol{P}_{x z}=\sum\limits_{i=0}^{2 n} W_{i}^{c}\left(\boldsymbol{X}_{k / k-1}^{i}-\hat{\boldsymbol{X}}_{k / k-1}\right) \cdot \\ \left(\boldsymbol{Z}_{k / k-1}^{i}-\hat{\boldsymbol{Z}}_{k / k-1}\right)^{\mathrm{T}}$ | (8) |
计算滤波增益:
| $\boldsymbol{K}_{k}=\boldsymbol{P}_{x z}\left(\boldsymbol{P}_{z z}\right)^{-1}$ | (9) |
利用式(9), 获得各个状态的误差修正量,状态和方差更新为:
| $\hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{K}_{k}\left(\boldsymbol{Z}_{k}-\hat{\boldsymbol{Z}}_{k / k-1}\right)$ | (10) |
| $\boldsymbol{P}_{k}=\boldsymbol{P}_{k / k-1}-\boldsymbol{K}_{k} \boldsymbol{P}_{x z}^{\mathrm{T}}$ | (11) |
6) 循环跳转。k=k+1, 返回步骤2), 进行下一次循环,直至循环结束。
1.2 UKF算法存在的问题对滤波器初始值的选取较为敏感是UKF算法存在的一个问题。从UKF算法的计算步骤可以看出,如果初始值选取出现偏差,会导致sigma点集χ0i出现偏差,而χ0i经过状态方程得到系统状态χk/k-1i, 偏差传递至式(3), 即状态预测均值
系统状态模型异常扰动对滤波精度带来的影响是UKF存在的另一个问题。从计算步骤来看,如果系统状态模型异常扰动,则系统状态Xk/k-1i存在异常,异常传递至式(3)和式(6), 即状态预测均值和量测预测均值存在异常,从而导致式(4)、式(7)和式(8)出现异常。
2 改进的UKF滤波算法针对UKF算法使用中存在的问题,将自适应估计原理引入UKF算法中,得到一种改进算法。该算法采取方差膨胀的方法,将存在偏差的
引入自适应因子ω, 将UKF算法计算步骤中的式(4)、式(7)和式(8)改写为:
| $\boldsymbol{P}_{k / k-1}=\frac{1}{\omega} \sum\limits_{i=0}^{2 n} W_{i}^{c}\left(\boldsymbol{X}_{k / k-1}^{i}-\hat{\boldsymbol{X}}_{k / k-1}\right) \cdot \\ \left(\boldsymbol{X}_{k / k-1}^{i}-\hat{\boldsymbol{X}}_{k / k-1}\right)^{\mathrm{T}}$ | (12) |
| $\boldsymbol{P}_{z z}=\frac{1}{\omega} \sum\limits_{i=0}^{2 n} W_{i}^{c}\left(\boldsymbol{Z}_{k / k-1}^{i}-\hat{\boldsymbol{Z}}_{k / k-1}\right) \cdot \\ \left(\boldsymbol{Z}_{k / k-1}^{i}-\hat{\boldsymbol{Z}}_{k / k-1}\right)^{\mathrm{T}}$ | (13) |
| $\boldsymbol{P}_{x z}=\frac{1}{\omega} \sum\limits_{i=0}^{2 n} W_{i}^{c}\left(\boldsymbol{X}_{k / k-1}^{i}-\hat{\boldsymbol{X}}_{k / k-1}\right) \cdot \\ \left(\boldsymbol{Z}_{k / k-1}^{i}-\hat{\boldsymbol{Z}}_{k / k-1}\right)^{\mathrm{T}}$ | (14) |
定义预测残留向量
自适应因子ω的作用是通过判断系统正常与否,在出现异常时能够自发调节状态预测信息和量测信息在滤波解中的权值比重,从而降低异常对滤波造成的影响。ω的取值如式(15)所示,式中的协方差矩阵Pzz按照改写前的式(7)取值:
| $\omega=\left\{\begin{array}{l}1, \operatorname{tr}\left(\boldsymbol{B}_{k} \boldsymbol{B}_{k}^{\mathrm{T}}\right) \leqslant \operatorname{tr}\left(\boldsymbol{P}_{z z}\right) \\ \frac{\operatorname{tr}\left(\boldsymbol{P}_{z z}\right)}{\operatorname{tr}\left(\boldsymbol{B}_{k} \boldsymbol{B}_{k}^{\mathrm{T}}\right)}, \operatorname{tr}\left(\boldsymbol{B}_{k} \boldsymbol{B}_{k}^{\mathrm{T}}\right)>\operatorname{tr}\left(\boldsymbol{P}_{z z}\right)\end{array}\right.$ | (15) |
由改进的UKF算法流程分析自适应因子ω的作用如下:1)当选取的初始值不存在偏差并且系统状态模型正常时,自适应因子ω将等于1, 系统按照正常的UKF算法进行滤波;2)当选取的初始值存在偏差或者系统状态模型存在异常扰动时,自适应因子ω将小于1, 状态预测对最终滤波解的贡献变小;3)当系统状态模型扰动明显异常时,ω将接近0, 系统状态模型信息几乎被完全弃用。
从改进过程可以看出,ω可以利用预报残留Bk和观测信息Zk来自适应调节Xk/k-1i在导航解中的比重,从而减少初值偏差和模型异常扰动对导航解的影响[5]。
3 BDS/SINS组合导航模型组合导航模型采用直接式滤波,以SINS机械编排方程为状态方程,使用导航参数作为被估状态,状态方程及量测方程无需进行线性化处理。
3.1 状态方程采用ENU地理坐标系作为导航坐标系,惯性导航系统采用指北方位机械编排,状态方程为:
| $\left\{\begin{array}{l}\boldsymbol{X}=f\left(\boldsymbol{X}(t), \boldsymbol{\omega}_{i b}^{b}, \boldsymbol{f}^{b}, t\right) \\ \boldsymbol{X}(t)=\left[\begin{array}{lllllllll}\gamma & \theta & \psi & v_{E} & v_{N} & v_{U} & L & \lambda & H\end{array}\right]^{\mathrm{T}}\end{array}\right.$ | (16) |
式中,X(t)是系统状态向量,9个参数分别为3个姿态(横滚、俯仰、航向)、三维速度(东向、北向、天向)和三维位置(纬度、经度、高度); 状态的方差阵为Pk; ωibb、fb分别为陀螺仪、加速度计的输出。依据SINS工作原理展开式如下:
| $\left\{\begin{array}{l}\boldsymbol{Q}_{k, j}=\mathrm{e}^{0.5\left[\Delta \theta_{j}\right]} \boldsymbol{Q}_{k-1, j}=\left[\begin{array}{llll}\lambda_{0} & \lambda_{1} & \lambda_{2} & \lambda_{3}\end{array}\right]^{\mathrm{T}} \\ {\left[\Delta \theta_{j}\right]=\int_{k-1}^{k} \boldsymbol{M}^{*}\left(\boldsymbol{\omega}_{i b}^{b}-\boldsymbol{C}_{n, j-1}^{b} \omega_{i n, j-1}^{n}+\boldsymbol{S}_{g, j}\right) \mathrm{d} t=\left[\begin{array}{cccc}0 & -\Delta \theta_{x, j} & -\Delta \theta_{y, j} & -\Delta \theta_{z, j} \\ \Delta \theta_{x, j} & 0 & \Delta \theta_{z, j} & -\Delta \theta_{y, j} \\ \Delta \theta_{y, j} & -\Delta \theta_{z, j} & 0 & \Delta \theta_{x, j} \\ \Delta \theta_{z, j} & \Delta \theta_{y, j} & -\Delta \theta_{x, j} & 0\end{array}\right]} \\ \boldsymbol{C}_{b, j}^{n}= {\left[\begin{array}{ccc}\lambda_{0}^{2}+\lambda_{1}^{2}-\lambda_{2}^{2}-\lambda_{3}^{2} & 2\left(\lambda_{1} \lambda_{2}+\lambda_{0} \lambda_{3}\right) & 2\left(\lambda_{1} \lambda_{3}-\lambda_{0} \lambda_{2}\right) \\ 2\left(\lambda_{1} \lambda_{2}-\lambda_{0} \lambda_{3}\right) & \lambda_{0}^{2}-\lambda_{1}^{2}+\lambda_{2}^{2}-\lambda_{3}^{2} & 2\left(\lambda_{2} \lambda_{3}+\lambda_{0} \lambda_{1}\right) \\ 2\left(\lambda_{1} \lambda_{3}+\lambda_{0} \lambda_{2}\right) & 2\left(\lambda_{2} \lambda_{3}-\lambda_{0} \lambda_{1}\right) & \lambda_{0}^{2}-\lambda_{1}^{2}-\lambda_{2}^{2}+\lambda_{3}^{2}\end{array}\right]} \\ \boldsymbol{v}_{k, j}=\boldsymbol{v}_{k-1, j}+\left(\boldsymbol{C}_{b, j}^{n}\left(\boldsymbol{f}^{b}+\boldsymbol{S}_{a, j}\right)+\boldsymbol{g}^{n}-\left(2 \boldsymbol{\omega}_{ie}^{n}+\boldsymbol{\omega}_{e n, j}^{n}\right) \times \boldsymbol{v}_{k-1}^{n}\right) \Delta t \\ \boldsymbol{P}_{k, j}=\boldsymbol{P}_{k-1, j}+\boldsymbol{v}_{k, j} \Delta t\end{array}\right.$ | (17) |
滤波过程中,噪声进入非线性系统,参与状态转移,将系统噪声和量测噪声与状态向量一起组成增广向量Xa, 维数n为21, 增广的方差阵为Pa:
| $\left\{\begin{array}{l}\boldsymbol{X}^{a}=\left[\begin{array}{ll}\boldsymbol{X}(t) & \boldsymbol{W}(t) & \boldsymbol{V}(t)\end{array}\right]^{\mathrm{T}} \\ \boldsymbol{P}^{a}=\left[\begin{array}{cc}\boldsymbol{P}_{k} & & 0 \\ & Q & \\ 0 & & \boldsymbol{R}\end{array}\right]\end{array}\right.$ | (18) |
式中,Sg, j、Sa, j分别为增广向量方差阵的平方根矩阵
以BDS输出的速度和位置作为观测向量,假设V为量测噪声,则量测方程为:
| $\left\{\begin{array}{l}\boldsymbol{Z}=\boldsymbol{H} \boldsymbol{X}+\boldsymbol{V} \\ \boldsymbol{Z}=\left[\begin{array}{llllll}v_{E} & v_{N} & v_{U} & L & \lambda & h\end{array}\right]^{\mathrm{T}} \\ \boldsymbol{H}=\left[\bf{0}_{6 \times 3} \quad \boldsymbol{I}_{6 \times 6}\right]\end{array}\right.$ | (19) |
以微小型飞行器作为载体构建仿真验证系统,飞行轨迹过程包括加速、爬升、平直飞行、转弯、下滑、盘旋等机动过程,仿真时间为3 600 s; 飞行器的初始姿态设定为:飞行器水平,航向为90°, 位置(118°, 29°, 50 m)。
根据目前在用的惯性器件性能,设定SINS参数和BDS测量精度,如表 1所示。
|
|
表 1 SINS参数和BDS测量精度 Tab. 1 Parameters of SINS and measure precision of BDS |
滤波初始参数设置为:三维姿态角误差均为0.5°/s, 三维速度误差均为0.1 m/s, 三维位置误差均为5 m。改进的UKF算法的相关滤波初始参数设置为:初始比例因子α=1, β=2, κ=0。
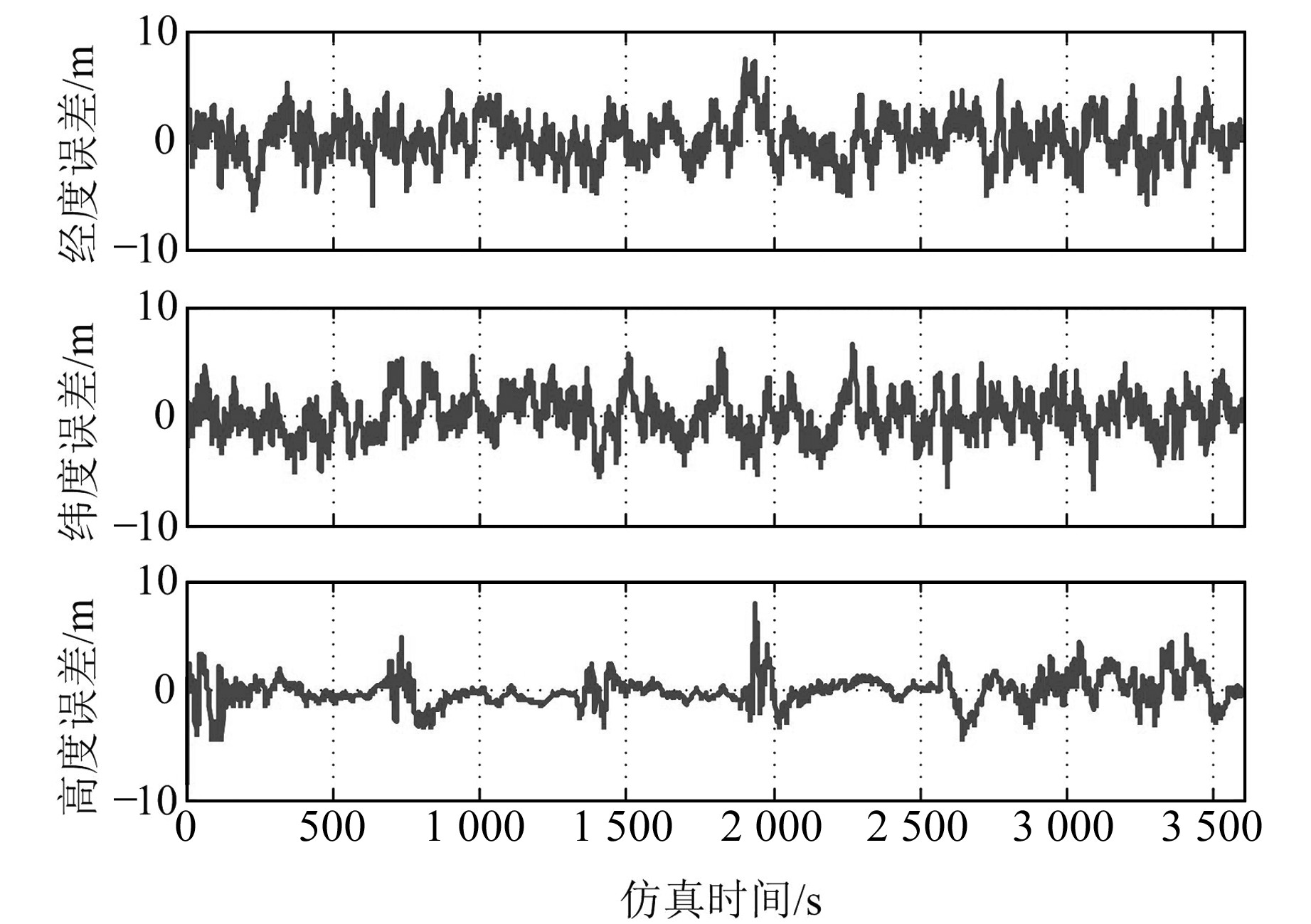
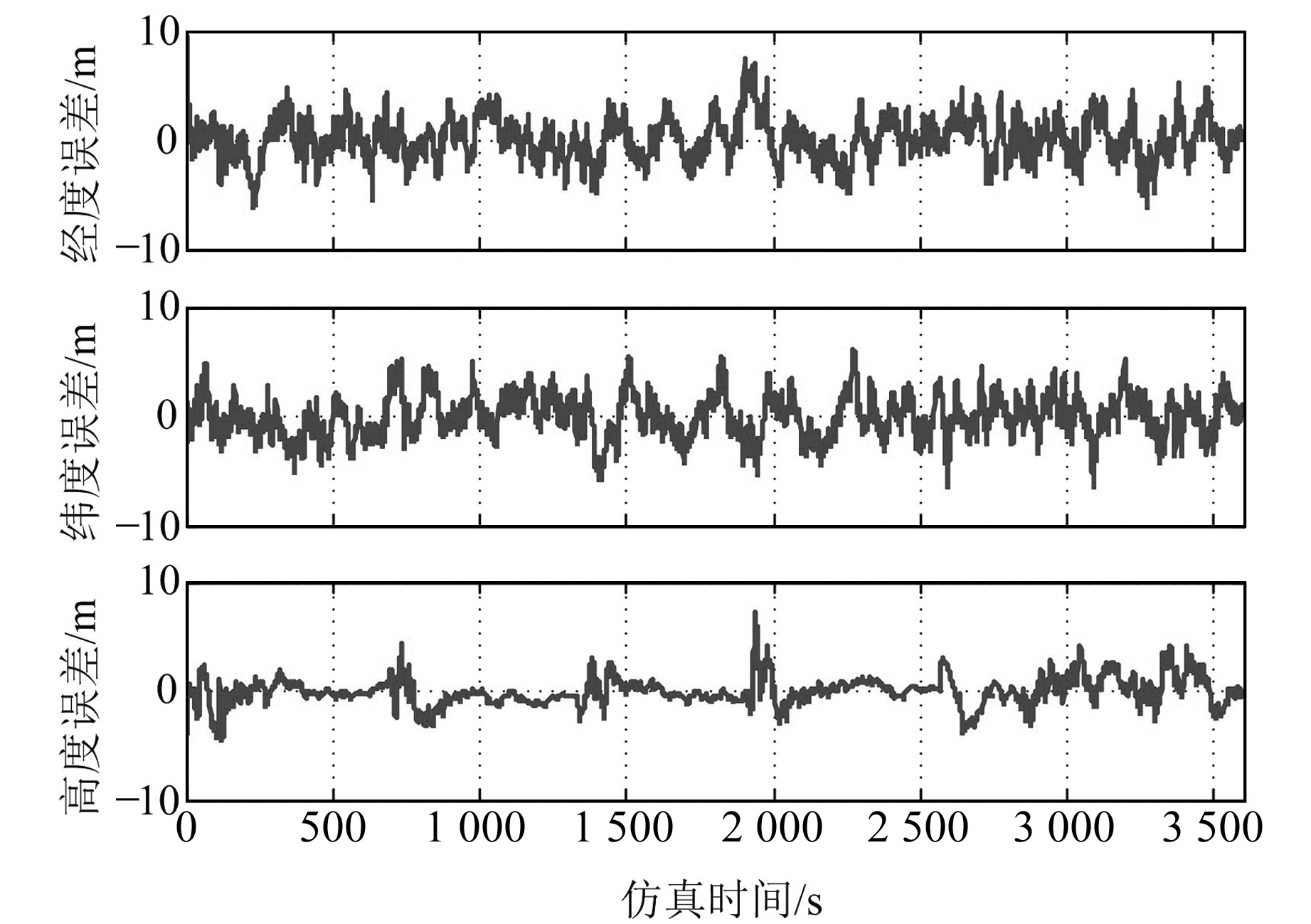
为便于滤波性能分析,在相同仿真条件下对相同的仿真原始数据分别使用UKF算法和改进的UKF算法,基于2种滤波方法的组合导航系统的各导航参数误差曲线如图 1、2所示(由于篇幅限制,此处仅给出位置误差曲线)。
|
图 1 基于UKF算法的位置误差曲线 Fig. 1 Position error curves based on UKF algorithm |
|
图 2 基于改进的UKF算法的位置误差曲线 Fig. 2 Position error curves based on improved UKF algorithm |
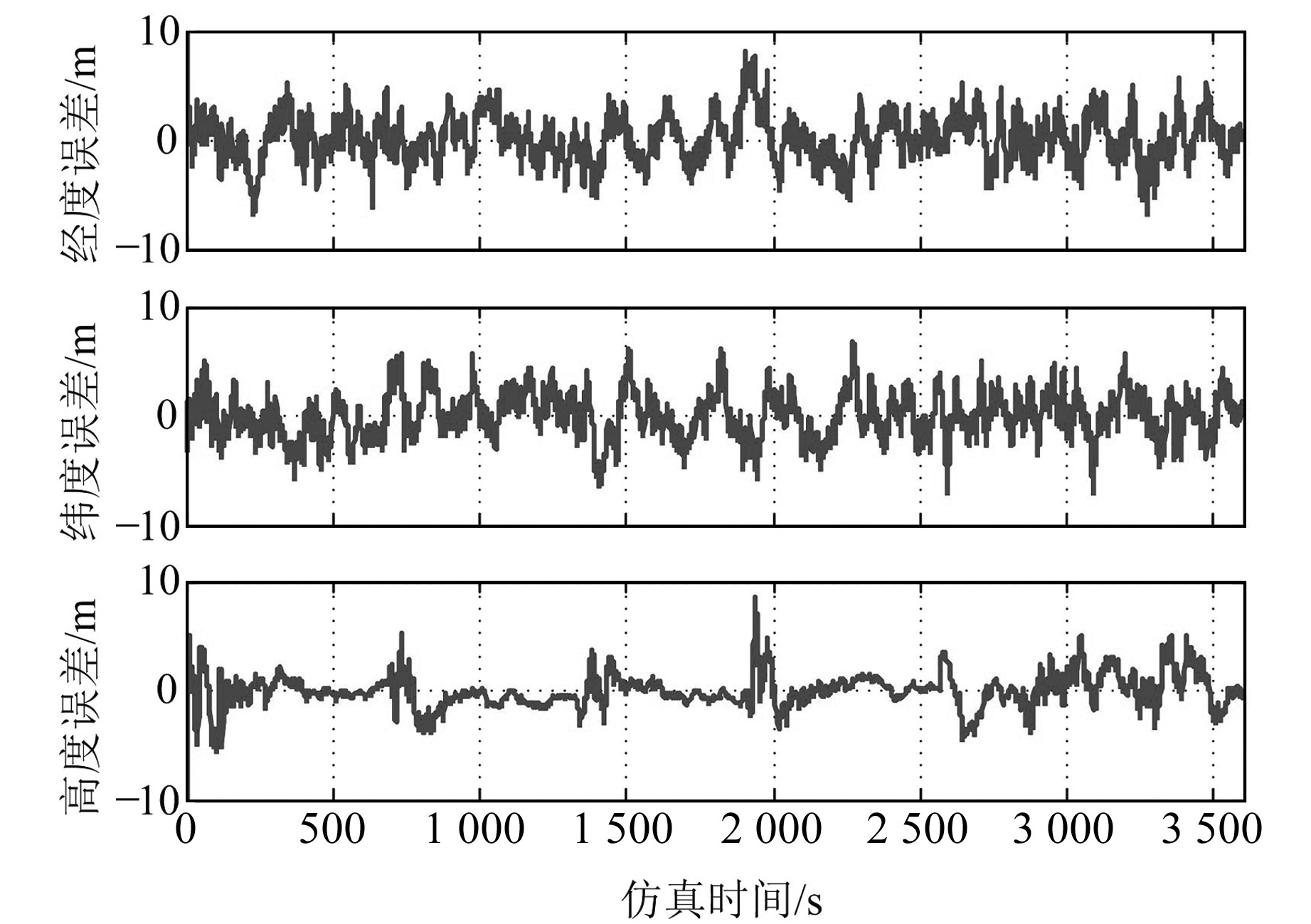
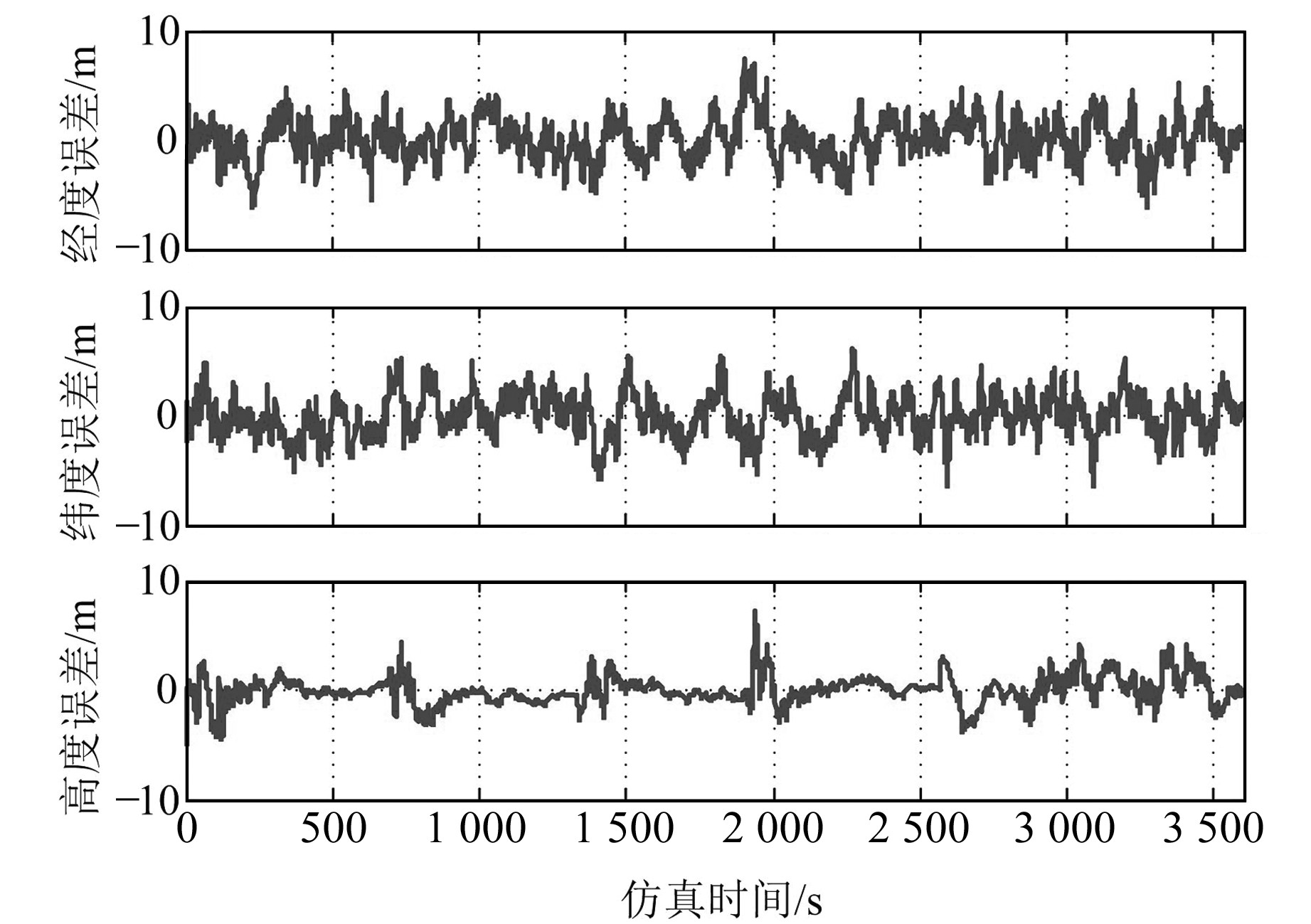
将初始误差扩大为上述仿真条件下初始误差的5倍,其他仿真参数不变,再次采用2种算法分别仿真,并进行分析与对比,其目的有2个:1) 通过改进的UKF算法的2次仿真可以较好地看出改进的UKF算法克服滤波初始误差的能力;2) 通过UKF算法的2次仿真可以看出滤波初始误差对UKF算法滤波精度的影响程度。2种滤波方法在5倍初始误差下的误差曲线图如图 3、4所示(同样,由于篇幅限制,此处仅给出位置误差曲线)。
|
图 3 基于UKF算法的位置误差曲线 Fig. 3 Position error curves based on UKF algorithm |
|
图 4 基于改进的UKF算法的误差曲线 Fig. 4 Position error curves based on improved UKF algorithm |
为了更加清楚地表达上述仿真分析,表 2列出了组合导航系统各导航参数误差在上述几种情况下的具体数值。
|
|
表 2 各导航参数误差比较 Tab. 2 Error comparison of navigation parameters |
从曲线图及表 2可以看出:
1) 对比单倍滤波器初始误差条件下2种算法的整个滤波过程可见,在许多时间点(段), 改进的UKF算法能够不同程度地降低各导航参数的误差波动幅度,说明改进的UKF算法在抑制系统状态模型异常扰动方面也发挥了一定作用。
2) 在单倍滤波器初始误差条件下,相对于UKF算法,在滤波初始阶段,改进的UKF算法对应的多个导航参数误差波动幅度明显变小;而在5倍滤波器初始误差条件下,相对于UKF算法,在滤波初始阶段,改进的UKF算法对应的导航参数误差波动幅度均明显变小,这说明改进的UKF算法能够较好地抑制初始值误差带来的影响。
3) 在单倍及5倍滤波器初始误差条件下,基于改进的UKF算法的组合导航参数误差的均方值、最大值、最小值均分别小于基于UKF算法的组合导航参数误差的均方值、最大值、最小值,进而说明相对于UKF算法,改进的UKF算法性能得到明显提升。
4) 对比单倍和5倍滤波器初始误差条件下改进的UKF算法,姿态、速度、位置误差在最值、均值、均方值等方面没有明显变化,仅在数值上有小幅波动。说明随着初始误差的增加,基于改进的UKF算法的组合导航各参数的误差变化较小,说明改进的UKF算法在抑制初始误差扰动方面性能较好。
以上分析表明,将自适应估计原理引入UKF算法中,能有效克服UKF算法存在的2个方面的问题,可明显提高导航精度,抑制滤波器初始误差对系统性能的影响。
5 结语文本研究了UKF滤波算法,将自适应估计原理与UKF算法相结合,得到一种改进的UKF算法。构建了BDS/SINS组合导航仿真验证系统,仿真结果验证了该改进算法的有效性。将改进的UKF滤波算法仿真曲线、数据与UKF算法的仿真曲线、数据进行对比发现,改进后的算法性能得到提升。
| [1] |
洪志强. 无迹卡尔曼滤波的改进算法及其在GPS/INS组合导航中的应用研究[D]. 南昌: 东华理工大学, 2019 (Hong Zhiqiang. Improved Algorithm of Unscented Kalman Filter and Its Application in GPS/INS Integrated Navigation[D]. Nanchang: East China University of Technology, 2019)
(  0) 0) |
| [2] |
王林, 林雪原. 基于UKF的GPS/SINS组合导航直接式滤波算法[J]. 导航定位与授时, 2015, 2(3): 43-48 (Wang Lin, Lin Xueyuan. Direct Kalman Filtering Algorithm for the GPS/SINS Integrated Navigation Based on UKF[J]. Navigation Positioning and Timing, 2015, 2(3): 43-48)
(  0) 0) |
| [3] |
Fakoorian S, Azimi V, Moosavi M, et al. Ground Reaction Force Estimation in Prosthetic Legs with Nonlinear Kalman Filtering Methods[J]. Journal of Dynamic Systems, Measurement, and Control, 2017, 139(11)
(  0) 0) |
| [4] |
黄平, 孙婷婷, 仝彦龙. 基于自适应的单形采样UKF组合导航算法[J]. 系统工程与电子技术, 2018, 40(7): 1 567-1 572 (Huang Ping, Sun Tingting, Tong Yanlong. UKF Integrated Navigation Algorithm Based on Adaptive Simplex Sampling[J]. Systems Engineering and Electronics, 2018, 40(7): 1 567-1 572)
(  0) 0) |
| [5] |
刘铮. UKF算法及其改进算法的研究[D]. 长沙: 中南大学, 2009 (Liu Zheng. UKF Algorithm and an Improved UKF Algorithm[D]. Changsha: Central South University, 2009)
(  0) 0) |
2. School of Chemical Engineering and Environment, Beijing Institute of Technology, 5 South-Zhongguancun Street, Beijing 100081, China
 2021, Vol. 41
2021, Vol. 41


