2. 东南大学微惯性仪表与先进导航技术教育部重点实验室, 南京市四牌楼2号, 210096;
3. 南通大学机械工程学院, 江苏省南通市啬园路9号, 226019
建立飞行区车辆管控系统有利于实现车辆的可视化、数字化、精细化管理[1], 车载定位系统能够实时准确地提供车辆行驶态势,是实现车辆监控管理的前提。在车载定位系统中组合使用捷联惯导系统(SINS)与全球卫星导航系统(GNSS), 可以获得车辆行驶速度、位置以及姿态等信息[2-3]。我国北斗导航系统已完成全球组网,正在推进其在民航领域的应用,差分北斗与SINS融合可为飞行区车辆管控系统提供高精度的位置服务。
当卫星信号有效时,SINS与GNSS融合能够获得车辆的行驶速度、位置等参数;当卫星信号受到遮挡时,组合导航系统精度会降低。刘鹏飞[4]提出一种里程计(DR)辅助的高精度GNSS/INS组合导航方法,并建立了GNSS/INS和DR/INS两种组合导航滤波模型,可根据车辆行驶环境切换滤波模式,具有长时间、高精度导航定位功能,但需要安装辅助导航设备,因此使用范围受限。张梦得等[5]针对GPS短时失效的问题提出一种基于偏最小二乘辅助高斯过程回归的SINS/GPS组合导航方法,但该方法的适用性还需进一步验证。Yao等[6]和张伦东等[7]提出一种基于零速修正技术(ZUPT)的组合导航方法,利用车辆停止或行人驻足时速度为0作为约束条件来估计SINS误差。胡杰等[8]提出利用车辆行驶中侧向和天向速度为0构造滤波器量测约束信息,称为动态零速修正技术(DZUPT), 但当车辆急速转弯时,侧向速度为0的假设条件不成立。周俊等[9]对GNSS/SINS组合导航算法进行研究,但未考虑卫星失效时引起系统精度降低的问题。近年来,部分学者[10-11]提出利用机器学习、深度学习等技术辅助SINS导航,但这些算法实现较为复杂,在使用中存在局限性。
本文针对飞行区车辆卫星信号断续或遮挡时导航系统精度降低的问题,利用ZUPT与DZUPT结合的运动学约束技术,提出一种基于车辆运动检测的差分北斗/SINS组合导航方法。针对车辆行驶特征给出组合导航系统框架,建立组合导航滤波状态方程与量测方程,根据SINS输出信息实现车辆运动状态的检测,并对该方法进行实验验证。
1 基于运动检测的差分北斗/SINS组合导航系统框架图 1为本文提出的飞行区车辆差分北斗/SINS组合导航系统框架。当北斗卫星信号有效时,组合导航滤波器利用差分北斗提供的速度、位置信息作为观测量进行滤波器量测更新,并根据估计得到的误差值反馈校正SINS。当北斗卫星信号受到遮挡时,要利用SINS提供的导航信息,首先需通过车辆运动状态检测模块来判断当前的车辆行驶状态(停车状态、直线行驶或拐弯行驶); 然后根据车辆运动学特性构造相应的运动约束信息(ZUPT模式、DZUPT模式或仅时间更新的DZUPT模式); 最后将构造得到的运动学约束辅助信息与SINS相组合,实现系统的误差估计与校正。
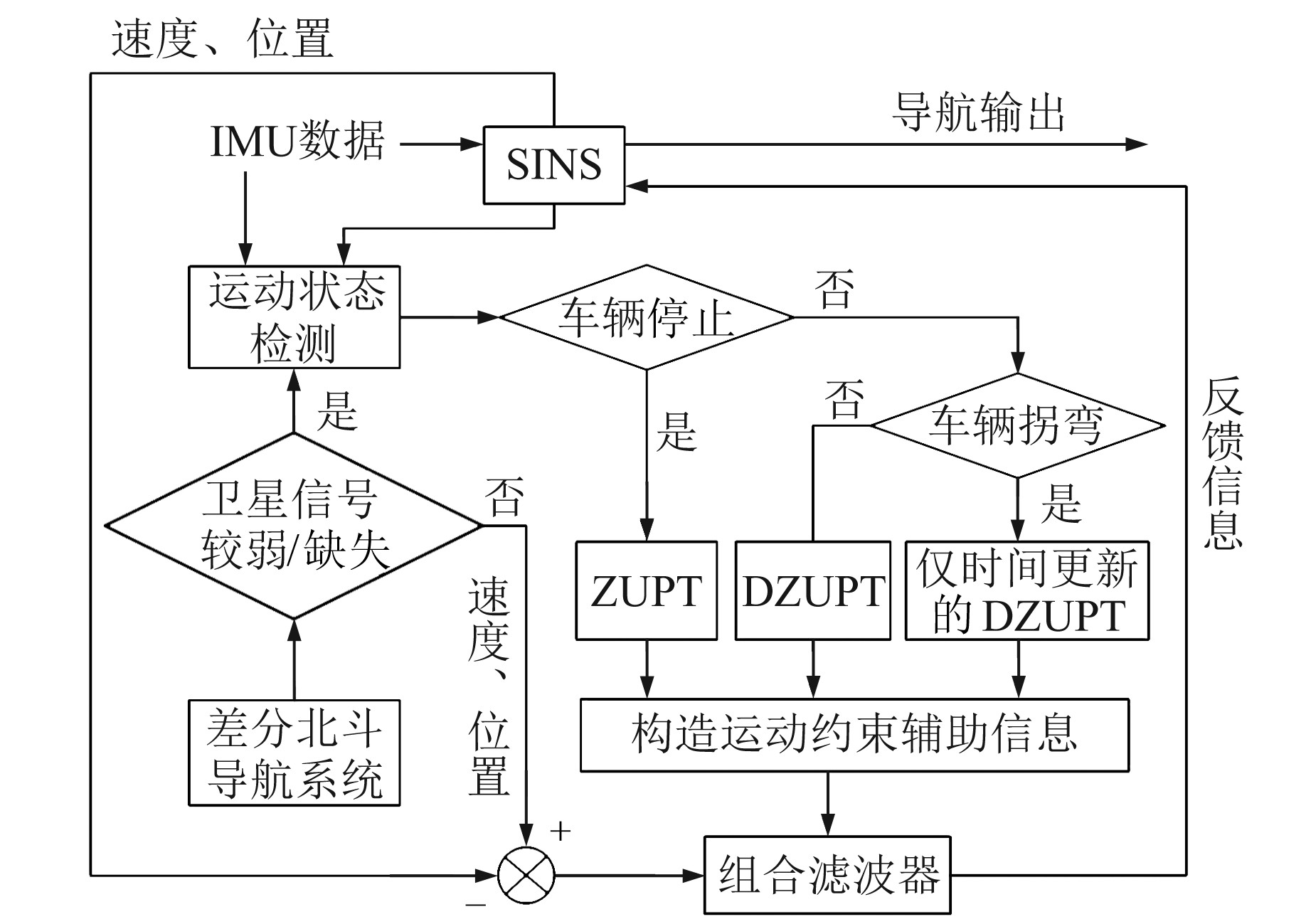
|
图 1 组合导航系统框架 Fig. 1 Frame of integrated navigation system |
本文导航坐标系选取东-北-天地理坐标系,记为n系,惯性坐标系记为i系,载体坐标系记为b系,其中oxb轴沿车体横轴指向右方,oyb轴沿车体纵轴指向前方,ozb轴垂直于车体向上,即构成一个右-前-上坐标系。
2.1 系统状态方程状态方程取15维状态量,依次为位置误差δL、δλ、δh, 速度误差δvE、δvN、δvU, 平台失准角ϕE、ϕN、ϕU, 陀螺常值漂移εx、εy、εz, 加速度计常值偏置▽x、▽y、▽z, 则状态向量X可表示为:
| $\boldsymbol{X}=\left[\mathrm{\delta} L \mathrm{\delta} \lambda \mathrm{\delta} h \mathrm{\delta} \boldsymbol{v}_{E} \mathrm{\delta} \boldsymbol{v}_{N} \delta \boldsymbol{v}_{U}\right. \\ \left.\mathrm{\phi}_{E} \mathrm{\phi}_{N} \mathrm{\phi}_{U} \varepsilon_{x} \varepsilon_{y} \varepsilon_{z} \quad \nabla_{x} \nabla_{y} \nabla_{z}\right]^{\mathrm{T}}$ | (1) |
进一步,由SINS误差方程可得到组合导航滤波状态方程为:
| $\dot{\boldsymbol{X}}=\boldsymbol{A} \boldsymbol{X}+\boldsymbol{W}$ | (2) |
式中,A为系统状态转移矩阵,可根据SINS误差确定;W为系统噪声向量。
2.2 系统量测方程 2.2.1 北斗卫星信号有效时当卫星信号有效时,将SINS输出速度、位置与北斗接收机输出速度、位置的差值作为Kalman滤波器测量值,此时滤波量测方程可表示为:
| $\boldsymbol{Z}_{1}=\boldsymbol{H}_{1} \boldsymbol{X}+\boldsymbol{V}_{1}$ | (3) |
式中,Z1为卫星信号有效时的量测向量;V1为系统量测噪声向量;H1为量测矩阵,可表示为:
| $\boldsymbol{H}_{1}=\left[\begin{array}{lll}\boldsymbol{I}_{3 \times 3} & \bf{0}_{3 \times 3} & \bf{0}_{3 \times 9} \\ \bf{0}_{3 \times 3} & \bf{I}_{3 \times 3} & \bf{0}_{3 \times 9}\end{array}\right]$ | (4) |
式中,I3×3表示3×3维单位矩阵;03×3、03×9分别表示3×3和3×9维零矩阵。
2.2.2 北斗卫星信号失效时当卫星信号失效且检测到车辆处于停止状态,即组合导航系统处于ZUPT模式时,利用车辆n系3个方向速度为0的特性构造滤波器量测值:
| $\boldsymbol{Z}_{2}=\left[\begin{array}{l}\delta \boldsymbol{v}_{E} \\ \delta \boldsymbol{v}_{N} \\ \delta \boldsymbol{v}_{U}\end{array}\right]=\left[\begin{array}{l}\boldsymbol{v}_{E} \\ \boldsymbol{v}_{N} \\ \boldsymbol{v}_{U}\end{array}\right]$ | (5) |
式中,Z2为卫星信号失效且车辆停止时的量测向量;δvE、δvN和δvU分别为n系3个方向的速度误差;vE、vN和vU分别为n系3个方向的速度值。
由式(5)可得到卫星信号失效且车辆处于停止状态时的量测方程为:
| $\boldsymbol{Z}_{2}=\boldsymbol{H}_{2} \boldsymbol{X}+\boldsymbol{V}_{2}$ | (6) |
式中,V2为系统量测噪声向量;H2为量测矩阵,可表示为:
| $\boldsymbol{H}_{2}=\left[\begin{array}{lll}\bf{0}_{3 \times 3} & \boldsymbol{I}_{3 \times 3} & \bf{0}_{3 \times 9}\end{array}\right]$ | (7) |
当卫星信号失效且车辆处于直线行驶,即组合导航系统处于DZUPT模式时,利用车辆运动学特性约束SINS误差。假设车辆无侧滑、跳跃等运动,则b系中侧向和天向速度可近似为0, 如图 2所示,该方法被称为非完整性约束[12]。
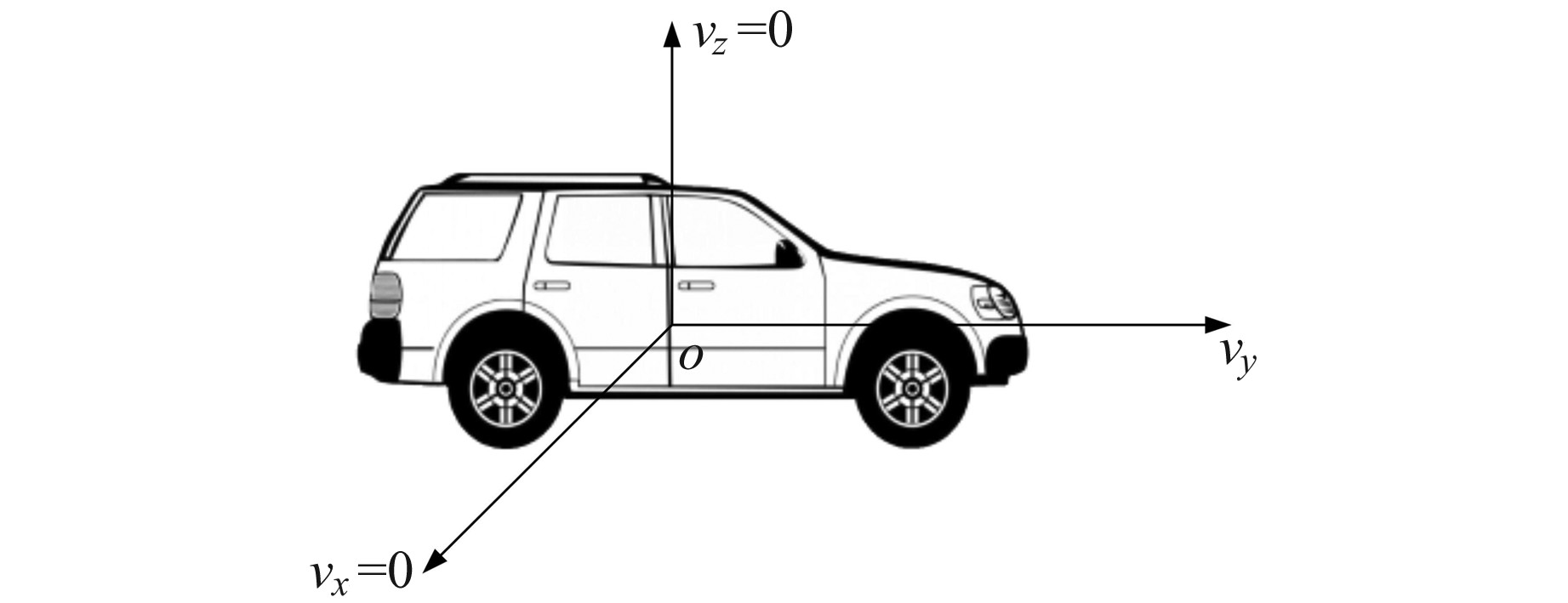
|
图 2 非完整性约束 Fig. 2 Non-holonomic constraint |
IMU经误差标校后其安装误差角一般可忽略,根据姿态矩阵Cnb可将n系速度转换到b系:
| $\boldsymbol{v}^{b}=\boldsymbol{C}_{n}^{b} \boldsymbol{v}^{n}$ | (8) |
式中,vb、vn分别为b系和n系车辆速度。由式(8)可得b系速度误差表达式为:
| $\delta \boldsymbol{v}^{b}=\boldsymbol{C}_{n}^{b}\left(\phi^{n} \times\right) \boldsymbol{v}^{n}+\boldsymbol{C}_{n}^{b} \delta \boldsymbol{v}^{n}=\boldsymbol{C}_{n}^{b} \delta \boldsymbol{v}^{n}-\boldsymbol{C}_{n}^{b}\left(\boldsymbol{v}^{n} \times\right) \phi^{n}$ | (9) |
式中,δvb、δvn分别为b系和n系速度误差;ϕn为平台失准角;vn×表示速度向量的斜对称矩阵。
式(9)可进一步表示为:
| $\delta \boldsymbol{v}^{b}=\boldsymbol{H}_{v, 1} \delta \boldsymbol{v}^{n}+\boldsymbol{H}_{v, 2} \phi^{n}$ | (10) |
其中,
| $\boldsymbol{H}_{v, 1}=\boldsymbol{C}_{n}^{b}$ | (11) |
| $\boldsymbol{H}_{v, 2}=-\boldsymbol{C}_{n}^{b}\left(\boldsymbol{v}^{n} \times\right)$ | (12) |
利用车辆非完整性约束条件可构造滤波器量测值为:
| $\boldsymbol{Z}_{3}=\left[\begin{array}{l}\delta v_{x}^{b} \\ \delta v_{z}^{b}\end{array}\right]=\left[\begin{array}{l}v_{x}^{b} \\ v_{z}^{b}\end{array}\right]$ | (13) |
式中,Z3为卫星失效时的观测向量;δvxb、δvzb分别为b系中沿x、z轴的速度误差;vxb、vzb分别为b系中沿x、z轴的速度分量。
由式(10)和式(13)可得量测方程为:
| $\boldsymbol{Z}_{3}=\boldsymbol{H}_{3} \boldsymbol{X}+\boldsymbol{V}_{3}$ | (14) |
式中,V3为系统量测噪声向量;H3为系统量测矩阵,可表示为:
| $\boldsymbol{H}_{3}= \\ \left[\begin{array}{lllll}\bf{0}_{1 \times 3} & \boldsymbol{H}_{v, 1}(1, *) & \boldsymbol{H}_{v, 2}(1, *) & \bf{0}_{1 \times 3} & \bf{0}_{1 \times 3} \\ \bf{0}_{1 \times 3} & \boldsymbol{H}_{v, 1}(3, *) & \boldsymbol{H}_{v, 2}(3, *) & \bf{0}_{1 \times 3} & \bf{0}_{1 \times 3}\end{array}\right]$ | (15) |
式中,Hv, 1(1, *)、Hv, 2(1, *)表示矩阵第1行;Hv, 1(3, *)、Hv, 2(3, *)表示矩阵第3行;01×3表示1×3维零矩阵。
3 运动状态检测根据分析可知,车辆状态可分为直线行驶、拐弯行驶和停止3种。当车辆停止时,可采用传统ZUPT进行误差约束;当车辆直线行驶时,利用车体侧向和天向速度为0进行非完整性约束;当车辆急速拐弯时,会产生较大的向心加速度,车体侧向和天向存在速度分量,不满足DZUPT约束条件,但一般情况下车辆拐弯时间较短,此时Kalman滤波算法需暂停量测更新,即组合导航系统处于仅时间更新的DZUPT模式。
假设k时刻IMU输出的车辆角速度和比力分别为ωk=[ωxk ωyk ωzk]T、fk=[fxk fyk fzk]T, 车辆运动状态检测的目的是根据IMU输出的信息确定当前车辆行驶状态,具体实现过程如下:
1) 确定停止状态阈值。在车辆初始对准阶段,采集3~5 min的IMU原始静态数据计算角速度和加速度检测阈值,表达式为:
| $\left\{\begin{array}{l}\lambda_{G}=\frac{1}{N} \sum\limits_{i=1}^{N}\left\|\boldsymbol{\omega}_{i}\right\|^{2} \\ \lambda_{A}=\frac{1}{N} \sum\limits_{i=1}^{N}\left(\left\|\boldsymbol{f}_{i}\right\|-g\right)^{2}\end{array}\right.$ | (16) |
式中,λG和λA分别为车辆停止时陀螺和加速度计的检测阈值;N为数据采集时间长度;ωi和fi(i=1, 2, …, N)分别为时间窗内i时刻IMU输出的陀螺和加速度计值;‖·‖表示2范数。
2) 判别车辆是否停止。滑动窗口时间取值为T, 根据IMU采样频率可求得T时间段内采样值,假设为M。实时计算滑动窗口内角速度和比力平均值,并与式(16)进行比较,以此来判断车辆是否停止:
| $L_{G}\left(\boldsymbol{\omega}_{k}, \boldsymbol{f}_{k}\right)=\frac{1}{M} \sum\limits_{i=k}^{k+M-1}\left\|\boldsymbol{\omega}_{i}\right\|^{2}$ | (17) |
| $L_{A}\left(\boldsymbol{\omega}_{k}, \boldsymbol{f}_{k}\right)=\frac{1}{M} \sum\limits_{i=k}^{k+M-1}\left(\left\|\boldsymbol{f}_{i}\right\|-g\right)^{2}$ | (18) |
式中,LG(·)和LA(·)分别为根据陀螺和加速度计输出求得的车辆停止检验值;g为当地重力加速度。判断车辆是否停止可认为是假设检验问题,当式(19)成立时,车辆即可被认为处于停止状态:
| $\left\{\begin{array}{l}L_{G}\left(\boldsymbol{\omega}_{k}, \boldsymbol{f}_{k}\right)<\lambda_{G} \\ L_{A}\left(\boldsymbol{\omega}_{k}, \boldsymbol{f}_{k}\right)<\lambda_{A}\end{array}\right.$ | (19) |
3) 判别车辆是否拐弯。由牛顿运动定律可确定车辆向心加速度为:
| $\boldsymbol{a}(t)=\boldsymbol{V}(t) \times \boldsymbol{\omega}_{z}(t)$ | (20) |
式中,a(t)为t时刻车辆向心加速度;V(t)为车辆行驶速度;ωz(t)为陀螺输出沿垂向拐弯角速度。
如果|a(t)|≥λa, 说明车体急速拐弯,此时将误差约束切换至仅时间更新的DZUPT模式,其中检测阈值λa由车辆实际行驶路况及车辆拐弯幅度确定。
4 车载实验车载验证实验装置由差分北斗/MEMS SINS组合导航系统、北斗差分基准站、北斗接收天线等组成,SINS中采用的MEMS陀螺仪零偏稳定性(1s平滑,1σ, 室温)优于5°/h, 加速度计零偏稳定性(1s平滑,1σ, 室温)优于100 μg。采用高精度Septentrio PolaRx5型GNSS接收机保存的星历和观测数据进行事后RTK差分处理,获得车辆参考行驶路线,数据更新频率为1 Hz, 位置精度优于0.05 m。
实验地点为某机场飞行区,利用专用移动通信网络实现北斗差分站与行驶车辆以及行驶车辆与监控席位之间的数字通信。图 3为车辆行驶轨迹,图 4为该时间段内北斗可见卫星个数及其几何精度因子曲线(GDOP), 图 5为差分北斗/SINS组合导航系统位置误差曲线,表 1为位置误差统计结果。
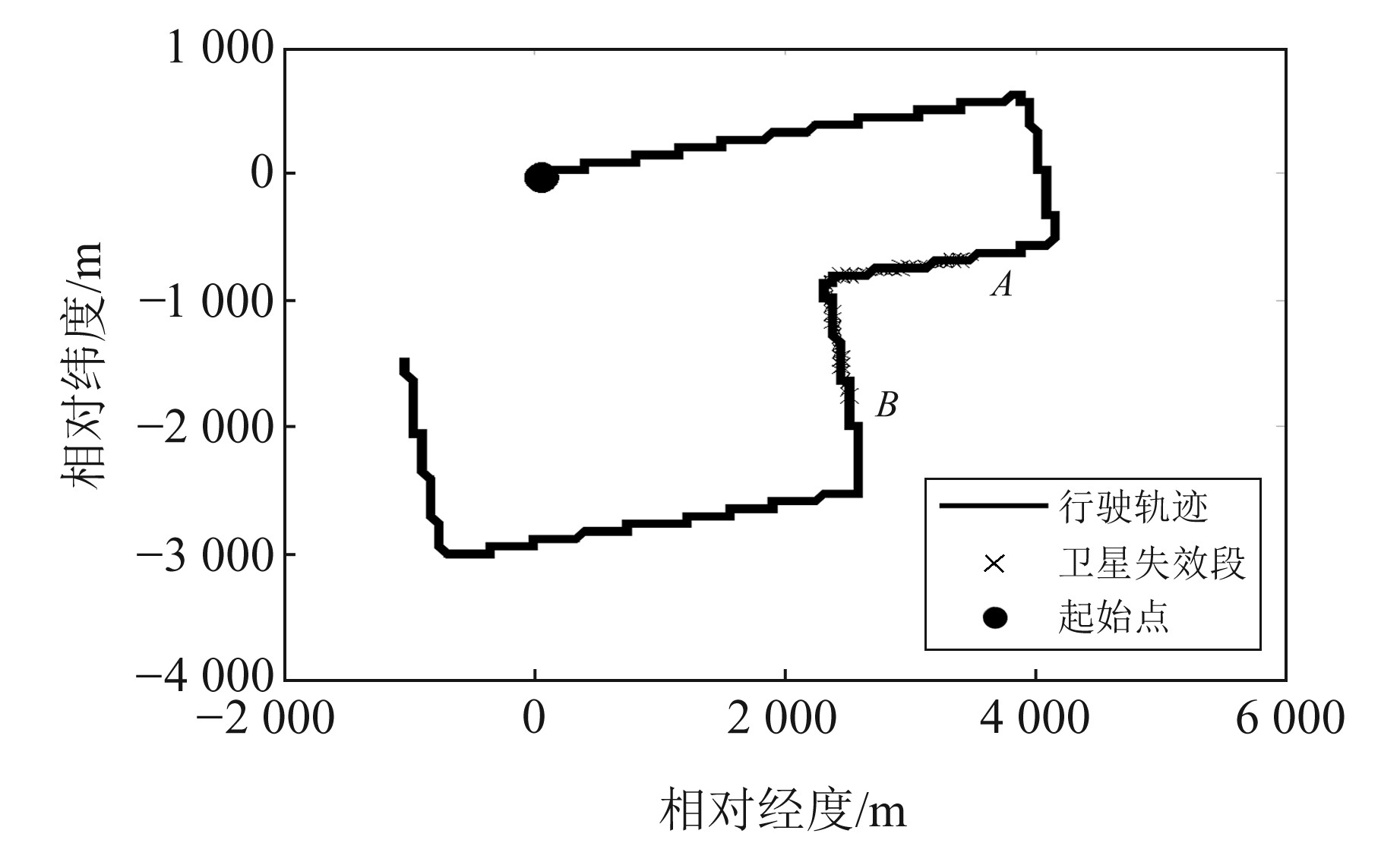
|
图 3 车辆行驶轨迹 Fig. 3 Vehicle track |
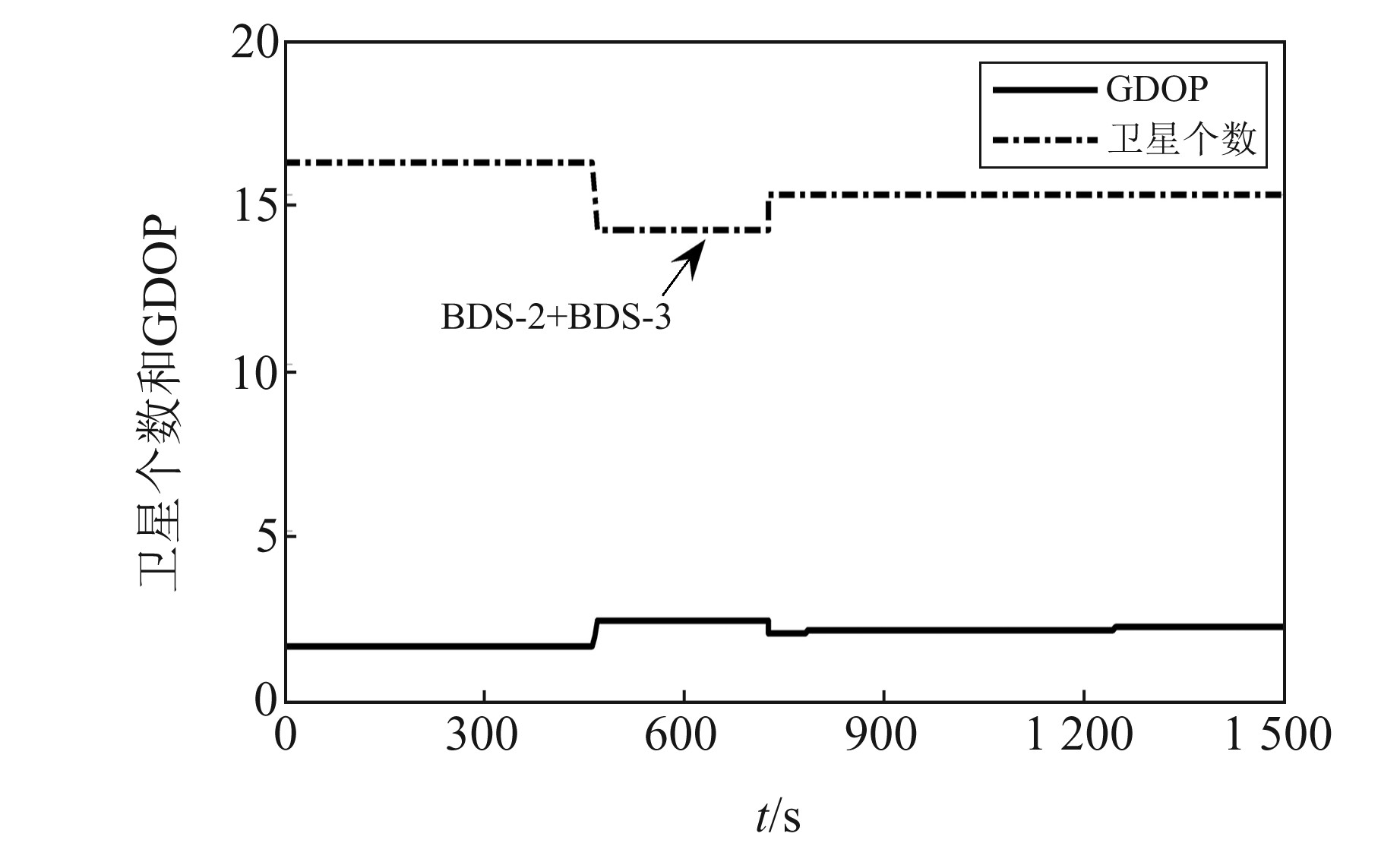
|
图 4 可见卫星个数及其GDOP Fig. 4 Numbers of visible satellites and their GDOP |

|
图 5 差分北斗/SINS组合导航位置误差 Fig. 5 Position errors of differential Beidou/SINS integrated navigation |
|
|
表 1 组合导航位置误差数值统计 Tab. 1 Numerical statistics of integrated navigationposition errors |
由图 4可以看出,该时间段内可见卫星个数最少为14颗,最多为16颗,满足差分定位需求;GDOP最大值为2.35, 卫星几何分布优。由图 5及表 1可以看出,组合导航系统的最大位置误差小于1 m, 表明差分北斗与SINS组合后能够为飞行区车辆管控系统提供亚米级精度位置服务。
为进一步模拟车辆在机场停机坪、廊桥等遮挡环境下的组合导航系统定位精度,利用保存的SINS和差分北斗数据,通过人为切断北斗接收机的卫星信号对本文提出的基于运动检测的DZUPT约束组合导航方法进行验证。行驶里程约为2.5 km, 时刻为605~919 s, 对应图 3中A-B行驶路段。该路段车辆行驶状态包括直线行驶、停车以及拐弯行驶等,传统DZUPT约束与本文提出的基于运动检测的DZUPT约束的位置误差对比曲线如图 6所示,表 2为2种约束方法的最大位置误差对比统计。
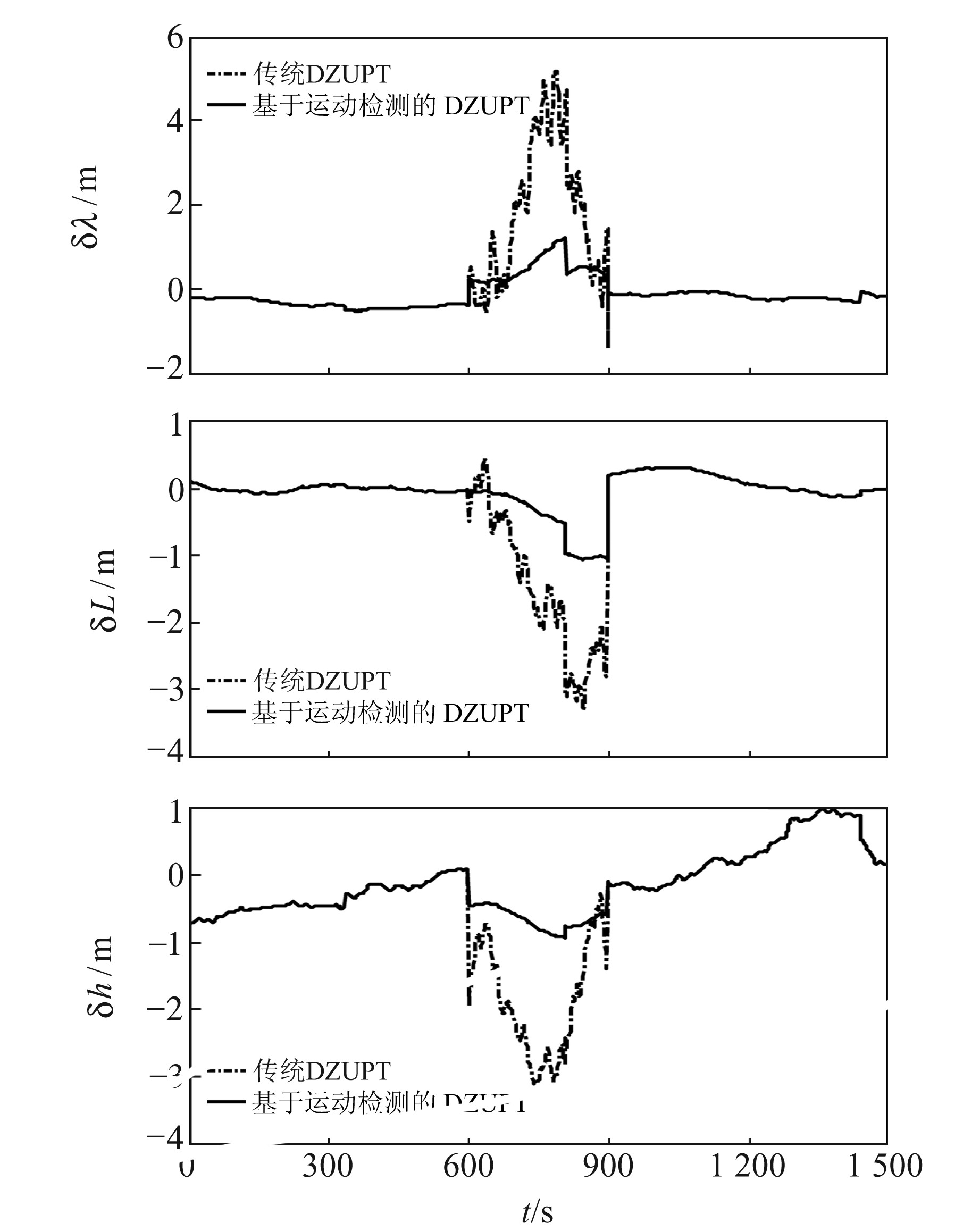
|
图 6 卫星信号失效时组合导航位置误差对比 Fig. 6 Comparison of position errors of integrated navigation under the satellite signal outage |
|
|
表 2 卫星信号失效时组合导航的最大位置误差对比 Tab. 2 Comparison of maximum position errors of integrated navigation under the satellite signal outage |
由图 6及表 2可以看出,当中断卫星信号并采用传统DZUPT约束辅助时,组合导航系统的经度误差最大为5.21 m, 引起误差的主要原因为拐弯时车辆侧向速度不为0, 传统DZUPT的约束条件不成立;当采用本文提出的基于运动检测的DZUPT约束辅助时,通过运动状态检测算法能够实时检测车辆的运动状态,当车辆拐弯时则切换滤波器至仅时间更新的DZUPT模式,可隔离车辆拐弯所引起的量测误差,经度最大误差减小为1.35 m, 从而提高了组合导航系统精度。
5 结语为进一步提高机场飞行区车辆组合导航精度,本文对北斗导航系统卫星信号中断时SINS位置误差随时间积累问题进行分析和研究。提出一种基于运动检测的DZUPT辅助约束SINS组合导航方法,当卫星信号中断时,利用惯性测量单元输出的陀螺和加速度计信息以及SINS输出的车辆速度来实现运动状态在线检测,从而切换组合导航系统至对应的辅助约束模式。
车载组合导航验证实验结果表明,当北斗导航系统卫星信号有效时,差分北斗与SINS组合定位精度优于1 m; 当卫星信号中断时,本文提出的基于运动检测的DZUPT辅助约束方法相比于传统DZUPT约束方法定位精度更高。
| [1] |
赵鸿铎, 李琛琛, 刘诗福, 等. 机场智慧飞行区内涵、分级与评价[J]. 同济大学学报: 自然科学版, 2019, 47(8): 1 137-1 142 (Zhao Hongduo, Li Chenchen, Liu Shifu, et al. Concept, Intelligence Rating, and Evaluation of Smart Airfield in Airport[J]. Journal of Tongji University: Natural Science, 2019, 47(8): 1 137-1 142)
(  0) 0) |
| [2] |
Zhang C, Guo C, Guo M Z. Information Fusion Based on Artificial Intelligence Method for SINS/GPS Integrated Navigation of Marine Vessel[J]. Journal of Electrical Engineering and Technology, 2020, 15(59): 1 345-1 356
(  0) 0) |
| [3] |
胡杰, 严勇杰, 石潇竹. 面向民用航空的SINS/DGPS组合导航融合方法[J]. 电光与控制, 2020, 27(4): 38-43 (Hu Jie, Yan Yongjie, Shi Xiaozhu. A Civil Aviation Oriented SINS/DGPS Fusion Method for Integrated Navigation[J]. Electronics Optics and Control, 2020, 27(4): 38-43)
(  0) 0) |
| [4] |
刘鹏飞. 里程计辅助的高精度车载GNSS/INS组合导航系统[J]. 光学精密工程, 2020, 28(4): 979-987 (Liu Pengfei. High-Precision Vehicle GNSS/INS Integrated Navigation System Aided by Odometer[J]. Optics and Precision Engineering, 2020, 28(4): 979-987)
(  0) 0) |
| [5] |
张梦得, 胡柏青, 田佳玉, 等. GPS短时失效条件下SINS/GPS组合导航数据处理方法[J]. 测绘科学技术学报, 2019, 36(5): 447-451 (Zhang Mengde, Hu Baiqing, Tian Jiayu, et al. The Data Processing Method of SINS/GPS Integrated Navigation under the Condition of GPS Short-Term Failure[J]. Journal of Geomatics Science and Technology, 2019, 36(5): 447-451)
(  0) 0) |
| [6] |
Yao Y Q, Xu X S, Xu X. An IMM-Aided ZUPT Methodology for an INS/DVL Integrated Navigation System[J]. Sensors, 2017, 17(9)
(  0) 0) |
| [7] |
张伦东, 卢晓慧, 李军正, 等. 基于零速修正的行人导航关键技术及研究进展[J]. 导航定位与授时, 2020, 7(3): 141-149 (Zhang Lundong, Lu Xiaohui, Li Junzheng, et al. The Key Technologies and Development of Pedestrian Navigation Based on ZUPT[J]. Navigation Positioning and Timing, 2020, 7(3): 141-149)
(  0) 0) |
| [8] |
胡杰, 严勇杰, 王子卉. 基于速度约束与模糊自适应滤波的车载组合导航[J]. 兵工学报, 2020, 41(2): 231-238 (Hu Jie, Yan Yongjie, Wang Zihui. Vehicle Integrated Navigation Based on Velocity Constraint and Fuzzy Adaptive Filtering[J]. Acta Armamentarii, 2020, 41(2): 231-238)
(  0) 0) |
| [9] |
周俊, 王琳, 徐永强, 等. 惯性导航与卫星导航组合定位精度分析及仿真[J]. 无线电工程, 2018, 48(12): 1 086-1 090 (Zhou Jun, Wang Lin, Xu Yongqiang, et al. Analysis and Simulation of Positioning Accuracy of Inertial/Satellite Integrated Navigation[J]. Radio Engineering, 2018, 48(12): 1 086-1 090)
(  0) 0) |
| [10] |
钱伟行, 周紫君, 谢非, 等. 基于机器学习与步态特征辅助的行人导航方法[J]. 中国惯性技术学报, 2019, 27(4): 433-439 (Qian Weixing, Zhou Zijun, Xie Fei, et al. Pedestrian Navigation Method Based on Machine Learning and Gait Feature Assistance[J]. Journal of Chinese Inertial Technology, 2019, 27(4): 433-439)
(  0) 0) |
| [11] |
Li J, Song N F, Yang G L, et al. Improving Positioning Accuracy of Vehicular Navigation System during GPS Outages Utilizing Ensemble Learning Algorithm[J]. Information Fusion, 2017, 35: 1-10 DOI:10.1016/j.inffus.2016.08.001
(  0) 0) |
| [12] |
Yang L, Li Y, Wu Y L, et al. An Enhanced MEMS-INS/GNSS Integrated System with Fault Detection and Exclusion Capability for Land Vehicle Navigation in Urban Areas[J]. GPS Solutions, 2014, 18(4): 593-603 DOI:10.1007/s10291-013-0357-1
(  0) 0) |
2. Key Laboratory of Micro-Inertial Instrument and Advanced Navigation Technology of Ministry of Education, Southeast University, 2 Sipailou, Nanjing 210096, China;
3. School of Mechanical Engineering, Nantong University, 9 Seyuan Road, Nantong 226019, China
 2021, Vol. 41
2021, Vol. 41

