就导航卫星而言,太阳光压是除二体中心引力、地球非球形引力及日月引力外最大的摄动力项,量级可达10-7m/s2[1-2]。因此,在导航卫星精密定轨中,建立太阳光压模型一直是一个重要的研究内容。欧洲定轨中心(Center of Orbit Determination in Europe, CODE)发布的ECOM光压模型属于经验型光压模型,是基于ROCK模型改进而来的。该模型使用较为广泛,可适用于BERNESE、GAMIT、PANDA等多款定轨软件。随着模型的不断修改,目前已发展出ECOM-2、ECOM-5、ECOM-7、ECOM-9等多种模型形式[3-5]。
美国麻省理工大学于2020-03更新的GAMIT软件采用了13个参数的ECOM新光压模型——ECOMC。由于该模型尚未被国内外学者研究,因此分析其定轨精度具有很高的科研意义。本文通过GAMIT10.71软件中的精密定轨模块,采用IGU超快速精密星历,以目前常用的ECOM-9光压模型作为参考,分析ECOMC光压模型对GPS卫星在R、A、C方向的定轨精度。同时,使用5种初始轨道精度不同的星历产品比较初始轨道对定轨精度的影响。GPS卫星类型见表 1。
|
|
表 1 GPS卫星类型(2020-06) Tab. 1 GPS satellite types(2020-06) |
一般使用DYB坐标系统描述太阳光压摄动力,其中D轴为卫星指向太阳的方向,Y轴为沿着卫星上太阳帆板的方向,并始终垂直于地球、卫星和太阳所确定的平面,B轴与D轴、Y轴构成右手坐标系。ECOM-9光压模型的实质是将太阳光压摄动力分解到D、Y、B方向上,并在各个方向进行傅里叶级数展开。ECOM-9光压模型的具体计算公式如下:
| $\boldsymbol{a}_{s}=\frac{a_{u}^{2}}{\left|\boldsymbol{r}_{s}-\boldsymbol{r}\right|}\left[D(u) \cdot \boldsymbol{e}_{D}+Y(u) \cdot\right. \\ \left.\boldsymbol{e}_{Y}+B(u) \cdot \boldsymbol{e}_{B}\right]$ | (1) |
其中,
| $D(u)=D_{0}[\lambda \operatorname{SRP}(1)+\operatorname{SRP}(4) \cos (u)+ \\ \operatorname{SRP}(7) \sin (u)] \\ Y(u)=D_{0}[\operatorname{SRP}(2)+\operatorname{SRP}(5) \cos (u)+ \\ \operatorname{SRP}(8) \sin (u)] \\ B(u)=D_{0}[\operatorname{SRP}(3)+\operatorname{SRP}(6) \cos (u)+ \\ \operatorname{SRP}(9) \sin (u)]$ | (2) |
式中,as为加速度;u为卫星在轨道面上距升交点的角度;λ为地影因子;au为天文长度,为1.495 978 707×1011 m; rs与r分别为地心惯性坐标系下太阳和卫星的位置;D0为与卫星型号有关的面质比参数,其取值与卫星型号以及卫星质量有关,这里将其与光压参数一起作为参数解算。设ex、ey和ez为星固坐标系的坐标轴单位向量,其中ez指向地球中心,3者之间的关系为:
| $\left\{\begin{array}{l}\boldsymbol{e}_{y}=\boldsymbol{e}_{z} \times \boldsymbol{e}_{D} \\ \boldsymbol{e}_{x}=\boldsymbol{e}_{y} \times \boldsymbol{e}_{z} \\ \boldsymbol{e}_{B}=\boldsymbol{e}_{D} \times \boldsymbol{e}_{z}\end{array}\right.$ | (3) |
SRP(1)、SRP(2)、SRP(3)为D、Y、B方向上的常数项,SRP(4)~SRP(9)为3轴方向上的周期摄动系数。SRP(1)~SRP(9)代表ECOM-9光压模型的9个参数[6]。
ECOMC光压模型是在ECOM-9光压模型基础上,在D方向上继续进行傅里叶级数展开,加入了2个2阶参数和2个4阶参数。光压模型的13个参数具体如下:
| $D(u)=D_{0}[\lambda \operatorname{SRP}(1)+\operatorname{SRP}(4) \cos (u)+ \\ \operatorname{SRP}(7) \sin (u)+\operatorname{SRP}(10) \cos (2 u)+ \\ \operatorname{SRP}(11) \sin (2 u)+\operatorname{SRP}(12) \cos (4 u)+ \\ \operatorname{SRP}(13) \sin (4 u)] \\ Y(u)=D_{0}[\operatorname{SRP}(2)+\operatorname{SRP}(5) \cos (u)+ \\ \operatorname{SRP}(8) \sin (u)] \\ B(u)=D_{0}[\operatorname{SRP}(3)+\operatorname{SRP}(6) \cos (u)+ \\ \operatorname{SRP}(9) \sin (u)]$ | (4) |
式中,SRP(10)~SRP(13)为ECOMC光压模型新增的4个参数。由于光压模型中的个别参数存在周期性变化,并且参数之间存在一定的强相关性[7], 因此,新增了4个参数的ECOMC光压模型对太阳光压在D、Y、B方向上的光压摄动力描述理论上会更加准确。
2 实验结果与分析 2.1 数据来源与解算策略按照连续性、稳定性、高精度、多种解、平衡性和精度一致性6个原则,使用间距分区法[8], 选择全球40个IGS站观测数据,计算2020年第099~101天的卫星轨道长弧段,并以IGS最终精密星历的结果作为真值,比较第100天中心弧段的卫星轨道结果与真值在R、A、C方向上的差值。
2.2 精度比较分析为了计算2020年第100天的GPS卫星轨道,采用定轨常用的3天解[9]计算方法。具体过程为:首先以2020年第099~101天的超快速星历产品的轨道参数为基础,将3 d的弧段合并到一起,进行3 d的GPS卫星轨道积分,获得卫星位置、运动速度、轨道初值等运动参数;然后利用当天的广播星历获得较为准确的卫星钟差,建立观测方程,获得精确的卫星轨道初值、力模型参数等其他待估参数;最后利用求解出的卫星轨道初值等参数对卫星运动方程进行积分,得到精确的卫星轨道,截取中间天(第100天)的轨道参数进行精度比较与分析。采用多天解弧段的优点在于定轨过程中削弱了边界效应的影响,提高了中心弧段的定轨精度。
以5种IGU产品作为原始轨道参数,分别使用ECOMC与ECOM-9光压模型对GPS卫星进行定轨,得到中间天的卫星轨道,并与IGS最终精密星历产品进行对比,比较32颗GPS卫星在径向、切向和法向的误差值(图 1)。

|
图 1 使用不同光压模型各卫星的定轨精度统计 Fig. 1 Orbit determination accuracy of each satellite in different solar radiation pressure models |
由图 1可见,随着5种IGU产品初始参数精度的不断提高,GPS卫星定轨精度也随之提高。IGU1、IGU2、IGU3、IGU4和IGU5在3个方向上的定轨精度分别达到5 cm、3.5 cm、2.5 cm、1.5 cm以及1.5 cm以内;初始轨道精度相同时,ECOMC光压模型的定轨精度优于ECOM-9光压模型;32颗GPS卫星中,个别卫星的定轨精度较低,可能与IGS提供的IGU产品中卫星初始精度有关;从轨道精度方向上看,卫星轨道径向精度高于切向和法向。
以IGS最终精密星历作为真值,统计解算后的32颗GPS卫星3个方向的误差均值,见表 2。可以看出,使用2种光压模型进行定轨,总体上径向精度最高,在1.5 cm以内;切向精度最低,在5 cm以内;法向精度在3 cm以内。ECOMC光压模型定轨精度在3个方向均优于ECOM-9光压模型,尤其在径向更明显。这是因为ECOMC光压模型比ECOM-9光压模型在径向增加了4个参数,因此对径向有进一步的约束。
|
|
表 2 不同光压模型对GPS卫星3个方向的误差均值统计 Tab. 2 The mean errors of all GPS satellite in threedirections calculated in different photopressure models |
为进一步验证ECOMC光压模型的定轨效果,以IGS最终精密星历产品作为真值,给出GPS卫星在第100天内96个历元下X、Y、Z方向的精度值。由于篇幅所限,只列出G01、G11、G22、G31这4类GPS卫星的轨道精度结果。根据不同的光压模型,设置3种计算方案:方案1, 使用ECOMC光压模型计算的卫星轨道与IGS最终卫星轨道之间的差值;方案2, 使用ECOM-9光压模型计算的卫星轨道与IGS最终卫星轨道之间的差值;方案3, 使用IGU1卫星轨道与IGS最终卫星轨道之间的差值。以单天96个历元作为横轴,各方向的误差值作为纵轴,统计各卫星各方案的精度值(图 2)。
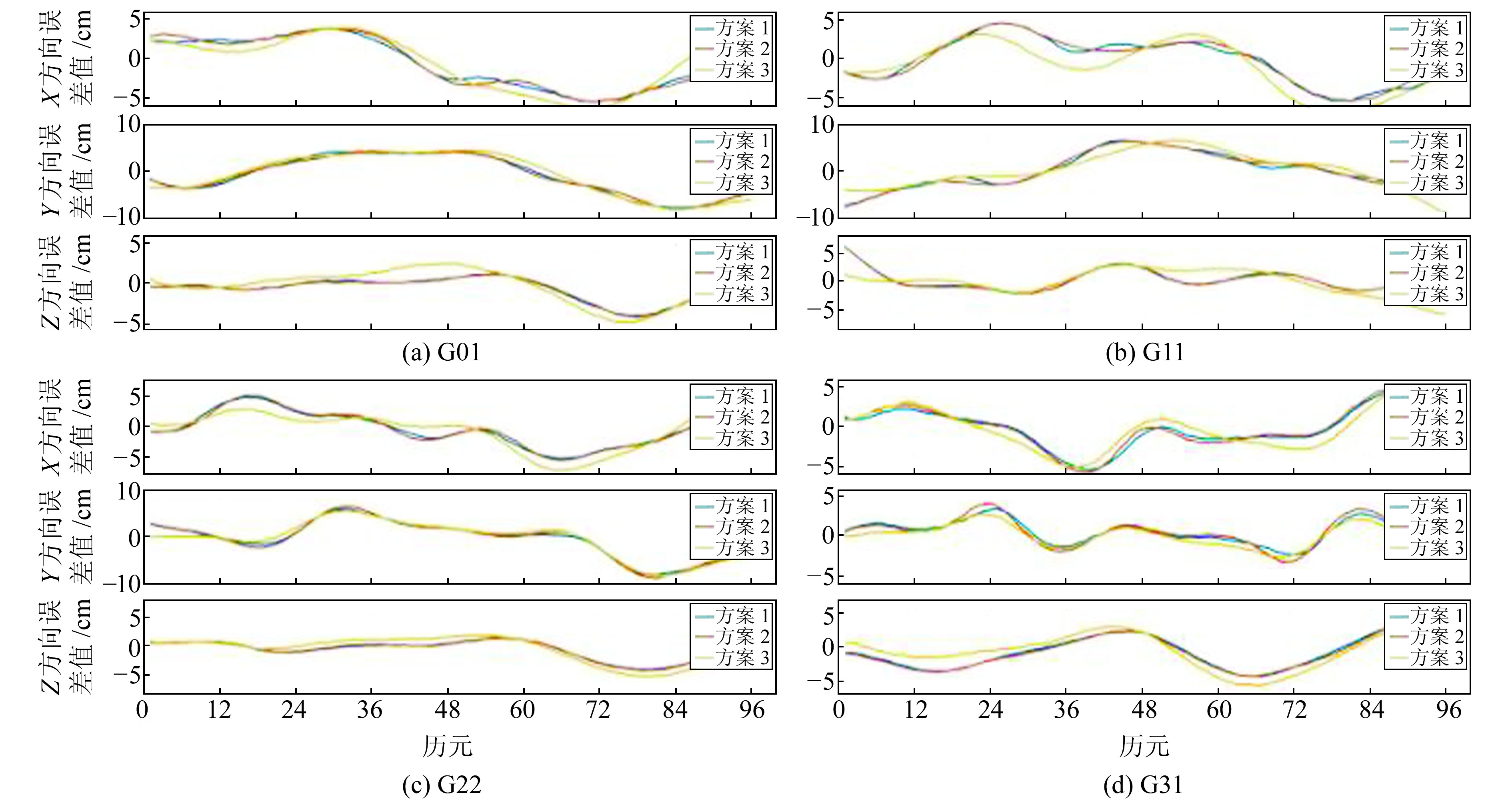
|
图 2 各卫星3个方向的精度统计 Fig. 2 Three-direction accuracy statistics of each satellite |
由图 2可见,采用2种光压模型对IGU1初始轨道进行解算,在每个历元下都有几mm的修正。由于ECOMC光压模型是在ECOM-9光压模型基础上新增了2个2阶参数和2个4阶参数,因此采用ECOMC光压模型对GPS卫星进行精密定轨,轨道精度会有所提高。
3 结语本文利用ECOMC光压模型和BERNE光压模型,分别使用5种IGU超快速精密星历对GPS卫星进行精密定轨,并对两者的定轨精度进行比较和分析,得出以下结论:
1) 由于ECOMC光压模型是在ECOM-9光压模型基础上在D方向上继续进行傅里叶级数展开,增加了4个参数,使得采用ECOMC光压模型定轨的精度优于ECOM-9光压模型,特别是在径向上提升效果更明显。与原始IGU1~IGU5初始轨道精度相比,新光压模型定轨精度分别为5 cm、3.5 cm、2.5 cm、2 cm和1.5 cm, 表现较好。
2) 对比5种IGU初始轨道的定轨结果发现,由于超快速精密星历观测部分的时长不断增加,定轨精度也不断提升,尤其是对于前3种IGU轨道,定轨精度提升明显。
3) 由于ECOM光压模型的实质是将太阳光压摄动力分解到D、Y、B方向上,并在3个方向上进行傅里叶级数展开,因此模型内参数之间有较强的相关性和周期特性,具体体现在定轨后每个卫星在每个历元下的轨道精度上。
| [1] |
Fliegel H F, Gallini T E. Solar Force Modeling of Block ⅡR Global Positioning System Satellites[J]. Journal of Spacecraft and Rockets, 1996, 33(6): 863-866 DOI:10.2514/3.26851
(  0) 0) |
| [2] |
Fliegel H F, Gallini T E, Swift E R. Global Positioning System Radiation Force Model for Geodetic Applications[J]. Journal of Geophysical Research: Solid Earth, 1992, 97(B1): 559-568 DOI:10.1029/91JB02564
(  0) 0) |
| [3] |
Beutler G, Brockmann E, Gurtner W, et al. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics(IGS): Theory and Initial Results[J]. European Respiratory Journal, 1994, 7(7): 1 350-1 364 DOI:10.1183/09031936.94.07071350
(  0) 0) |
| [4] |
Springer T A, Beutler G, Rothacher M. A New Solar Radiation Pressure Model for GPS Satellites[J]. GPS Solutions, 1999, 2(3): 50-62 DOI:10.1007/PL00012757
(  0) 0) |
| [5] |
Arnold D, Meindl M, Beutler G, et al. CODE's New Solar Radiation Pressure Model for GNSS Orbit Determination[J]. Journal of Geodesy, 2015, 89(8): 775-791 DOI:10.1007/s00190-015-0814-4
(  0) 0) |
| [6] |
韩德强. BDS卫星光压模型参数选取及偏航姿态调整[C]. 第10届中国卫星导航年会, 北京, 2019 (Selection of Solar Radiation Model Parameters and Yaw Attitude Adjustment of BDS Satellite[C]. The 10th China Satellite Navigation Conference, Beijing, 2019)
(  0) 0) |
| [7] |
刘永, 张传定, 李姗姗, 等. 基于IGS精密星历的BERNESE光压模型参数分析[J]. 测绘工程, 2016, 25(1): 29-33 (Liu Yong, Zhang Chuanding, Li Shanshan, et al. Analysis of BERN SRP Parameters Based on IGS Ephemeris[J]. Engineering of Surveying and Mapping, 2016, 25(1): 29-33)
(  0) 0) |
| [8] |
曹炳强, 成英燕, 许长辉, 等. 间距分区法在解算卫星连续运行站数据中的应用[J]. 测绘通报, 2016(11): 15-17 (Cao Bingqiang, Cheng Yingyan, Xu Changhui, et al. Application of Space Partition Method in the CORS Data Processing[J]. Bulletin of Surveying and Mapping, 2016(11): 15-17)
(  0) 0) |
| [9] |
王武星, 顾国华. 利用基准站观测资料确定GPS卫星轨道[J]. 大地测量与地球动力学, 2003, 23(3): 112-115 (Wang Wuxing, Gu Guohua. GPS Satellite Orbit Determination with Observational Data of Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2003, 23(3): 112-115)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

